Группа БУ-20 10.12.2020

Стр 1 из 2Следующая ⇒

Группа БУ-20 10. 12. 2020

Лекция 2.

Задание:

1. Прочитайте предложенный вам материал.

2. Запишите в тетрадь опорный конспект лекции с образцами решения примеров.

3. Фото своего конспекта отправить по ссылке В Контакте:
https: //vk. com/topic-193913663_46680465 до конца дня.

Тема 1: Определитель матрицы

Определитель можно вычислить только для квадратной матрицы

На практике чаще всего можно встретить определитель второго порядка, например: 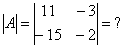, и определитель третьего порядка, например: .

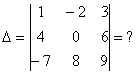Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

Обозначения: Если дана матрица 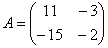, то ее определитель обозначают 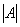. Также очень часто определитель обозначают латинской буквой 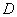или греческой .

Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Для этого нужно применить определенные правила, формулы и алгоритмы.

Начнем с определителя второго порядка («два» на «два»):

Формула для вычисления: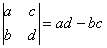

Сразу рассмотрим пример:

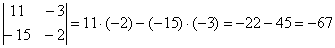
Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Определитель матрицы третьего порядка («три на три») можно раскрыть несколькими способами.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

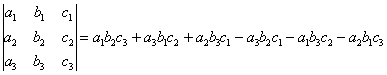
Пример:

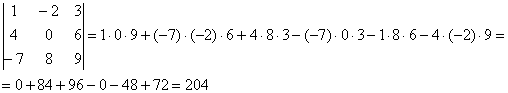
Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов?

Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».

Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

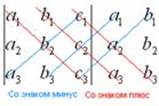
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

По правилу Саррюса, необходимо справа от вычисляемого определителя записать первые два столбца этого определителя и перемножить диагональные элементы. Взяв эти произведения с соответствующими знаками, получим, что искомый определитель третьего порядка равен

Пример:

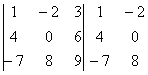
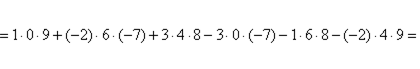
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

12 Следующая ⇒