
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Свойства равнобедренного треугольника. Признак равнобедренного треугольника.
Тема: Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Свойства равнобедренного треугольника. Признак равнобедренного треугольника.
Повторить с §16-18, стр. 32-36
Ознакомиться с образцами решения задач и записать их в рабочую тетрадь.
№105. Точки А и С лежат по одну сторону от прямой а. Перепендикуляры АВ и CD к прямой а равны.
А)Докажите, что АВD=;
Б) найдите если.


 А С
А С

В D а
Дано: а, А.
Доказать: 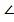 АВD =
АВD = 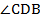 .
.
Найти: 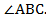
Доказательство.
Так как 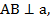 то
то 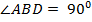 . Так как
. Так как 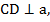 то
то 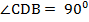 .
.
Так как 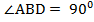 ,
, 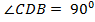 , то
, то 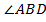 =
= 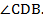
Так как АВ= 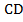 (по условию),
(по условию), 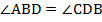 , BD - общая сторона, то Δ ABD=Δ BCD по I признаку равенства треугольников.
, BD - общая сторона, то Δ ABD=Δ BCD по I признаку равенства треугольников.
В равных треугольниках против равных сторон лежат равные углы и наоборот.
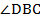 лежит против стороны CD в Δ BCD. В Δ ABD против стороны АВ лежит
лежит против стороны CD в Δ BCD. В Δ ABD против стороны АВ лежит 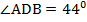 . Так как Δ BCD= Δ ABD, АВ= СD,
. Так как Δ BCD= Δ ABD, АВ= СD, 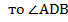 =
= 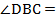
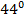 .
.
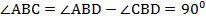 -
- 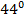 =
= 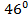 .
.
№106. МедианаAD продолжена за точку D на отрезок DE, равный AD, и точка Е соединена с точкой С.
А) Докажите, что Δ ABD=Δ ECD;
Б) Найдите если, .
 |



 В E
В E
D





 A C
A C
Дано: 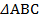 , AD- медиана, AD= DЕ,
, AD- медиана, AD= DЕ, 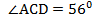 ,
, 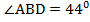 .
.
Доказать: что Δ ABD=Δ ECD.
Найти: 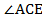 .
.
Решение.
Так как AD- медиана, ВD= DС.
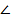 BDА=
BDА= 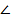 ЕDС по свойству вертикальных углов, ВD= DС, АD= DЕ (по построению).
ЕDС по свойству вертикальных углов, ВD= DС, АD= DЕ (по построению).
Тогда Δ ABD=Δ ECD по I признаку равенства треугольников.
Так как Δ ABD=Δ ECD, то равны углы, лежащие против равных сторон в этих треугольниках. В частности, 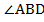 лежит против стороны АD в Δ ABD. Ей равна сторона DЕ в Δ ECD. Против стороны DЕ лежит
лежит против стороны АD в Δ ABD. Ей равна сторона DЕ в Δ ECD. Против стороны DЕ лежит 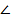 ЕСD. Тогда
ЕСD. Тогда 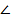 ЕСD=
ЕСD= 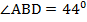 .
.
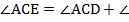 ЕСD =
ЕСD = 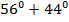 =
= 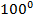 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|