
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Степенная функция с целым отрицательным показателем.
Степенная функция с целым отрицательным показателем.
Степенная функция вида: у = kх—n
называется степенной функцией с целым отрицательным показателем.
Рассмотрим функции при n=1 и n=2.
При n=1 получаем функцию вида y= 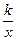 — эта функция называется гиперболой.
— эта функция называется гиперболой.
Рассмотрим свойства функции y= 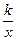 :
:
I. Область определения — D(f)=(-∞; 0)∪ (0; +∞ ).
II. Область значения — E(f)=(-∞; 0)∪ (0; +∞ ).
III. Нечётная, так как f( — х) = k/( — x) = —k/x = —f (х)
IV. При k > 0 на промежутке (-∞; 0)∪ (0; +∞ ) функция убывает, а при k < 0 на промежутке (-∞; 0)∪ (0; +∞ ) функция возрастает.
V. Экстремумов нет.
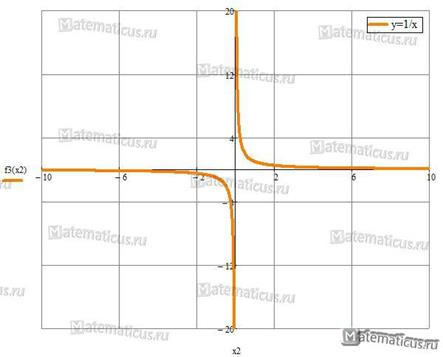
График гиперболы y= 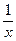
При n=-2 и k=1 получаем функцию вида y=  .
.
Рассмотрим свойства функции y=  :
:
I. Область определения — D(f)=(-∞; 0)∪ (0; +∞ ).
II. Область значения — E(f)=(0; +∞ ).
III. Чётная.
IV. Функция убывает на промежутке (0; +∞ ) и возрастает на промежутке (-∞; 0).
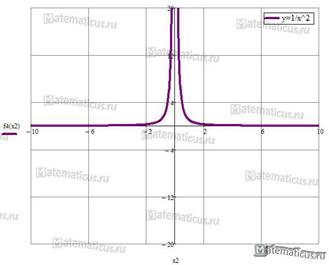
График функции y= 
Рассмотрим элементарную функцию с корнем y= 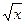
Свойства функции y= 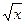
I. Область определения — D(f)=[0; +∞ ).
II. Область значения — E(f)=[0; +∞ ).
III. Функция ни чётная, ни нечётная.
IV. Функция возрастает на [0; +∞ ).
V. Экстремумов нет.
VI. Корень x=0
VII. Экстремумы функции — min при x=0.
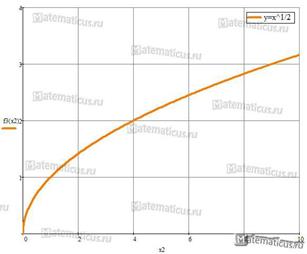
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|