
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
5.5.Рациональные формы сечения балок
ПЛАКАТ 5
Рассмотрим наш пример:
Ми=МХ= - FZ
Уравнение изогнутой оси – упругой линии балки:
E·I y''= - FZ
Интегрируем
 I интеграл
I интеграл
 II интеграл
II интеграл
Определяем постоянные интегрирования:
в заделке - точка «B» угол θ В=0= у'z=l; прогиб уz=l =0;


Тогда уравнение углов поворота:
 ;
;
уравнение прогибов:
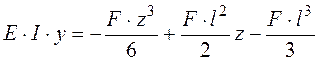 .
.
Максимальный прогиб и угол поворота будут при z=0:
 →
→ 
Знак «+»значит угол θ откладывается против часовой стрелки.
 →
→ 
Знак «–»значит прогиб f направлен вниз (против оси Y).
ПЛАКАТ 6
5. 5. Рациональные формы сечения балок
Наиболее выгодными сечениями балок с точки зрения затрат материала являются такие, у которых наибольшая доля материала размещена в верхней и нижних частях сечениях, где напряжение наибольшее. При этом будет наиболее полно использоваться материал балки.
Для количественной оценки рациональности сечения служит безразмерная величина, называемая осевым удельным моментом сопротивления.
 (5. 19)
(5. 19)

5. 6. Рациональное размещение опор
ПЛАКАТ 7
С точки зрения экономии материала кроме формы сечения балки имеет еще существенное значение правильное размещение опор балок.
 Рассмотрим однопролетную балку, нагруженную распределенной нагрузкой:
Рассмотрим однопролетную балку, нагруженную распределенной нагрузкой:
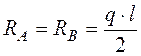

Если изменить расположение опор, то эпюра Ми будет иметь вид:
Приравняв изгибающие моменты по модулю в опорах и по середине балки, найдем размер «а»:
a = 0, 207·l
при этом:

т. е. в 5, 8 раза меньше, чем когда опоры расположены на краях балки.
При расчете этой балки на жесткость, размер а = 0, 223·l, при этом максимальный прогиб балки уменьшится в 13, 7 раза.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|