Лекция 5 (Часть2). ПЛАКАТ 1,2,3. 5.4 Определение перемещений при изгибе.. ПЛАКАТ 4

Лекция 5 (Часть2)

ПЛАКАТ 1, 2, 3

5. 4 Определение перемещений при изгибе.

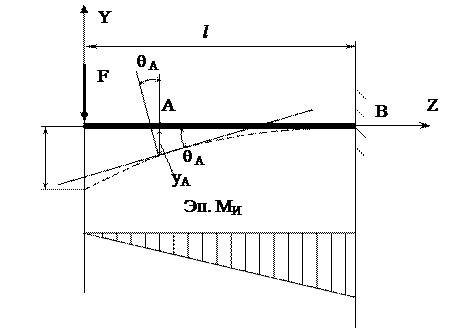
При изгибе происходит искривление оси балки, в связи, с чем в инженерной практике приходится проводить расчет балок при изгибе не только на прочность, но и на жесткость. При изгибе происходят перемещения двух видов: линейные и угловые.

Линейное перемещение называется прогибом – это перемещение центра тяжести сечения по направлению перпендикулярно к оси балки:

y= U(z); y_max=f

Угол θ , на который поворачивается сечение относительно своего первоначального положения, называется углом поворота сечения:

θ = V(z)

Искривленная при изгибе ось балки называется упругой линией балки.

Если известно уравнение y=U(z) упругой линии балки, то определение прогиба не представляет затруднений.

Известно, что тангенс угла наклона касательной к плоской кривой в данной точке равен первой производной y по z:

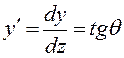В пределах упругой деформации когда θ < 0, 01 рад можно принять:

tg θ ≈ θ, тогда у'= θ. (5. 13)

Из рисунка видно, что угол поворота сечения равен углу наклона касательной.

ПЛАКАТ 4

Кривизна оси балки определяется соотношением (5. 8):

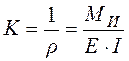(5. 8)

а из математики известно, что:

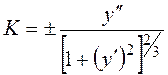(5. 14)

Приравнивая правые части (5. 8) и (5. 14) получим точное дифференциальное уравнение упругой линии балки (изогнутой оси):

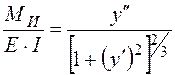(5. 15)

Учитывая, что при у'= θ < 0, 01, величина (у')² - ничтожно мала; упростим выражение (5. 15):

E·I·y''=М_И(5. 16)

При этом ось «y» всегда направлена вверх. Если прогиб направлен вверх по оси y, то он положительный «+»; если вниз – отрицательный «–». Знак изгибающего момента ставится по прежнему правилу.

Интегрируя уравнение (5. 16), учитывая, что у'= θ получаем уравнение углов поворота:

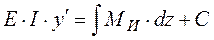(5. 17)

Интегрируя второй раз, получаем уравнение прогибов:

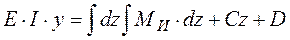(5. 18)

где С и D - постоянные интегрирования, определяемые из граничных условий, каковыми являются условия опирания балки (закрепления балки).

12 3 Следующая ⇒