
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Разрывы функции. Разрыв первого рода. Разрыв второго рода. Свойства функции, непрерывной на замкнутом отрезке. Задания для самостоятельного решения (домашнее задание)
Разрывы функции
Разрыв первого рода
Пусть 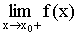 и
и 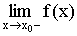 существуют:
существуют:
I. Если 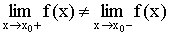 , то в точке
, то в точке 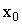 функция
функция
испытывает разрыв скачок первого рода.
Примеры:
1.
1. 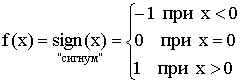
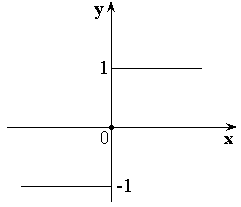
2.  – целая часть числа x.
– целая часть числа x.
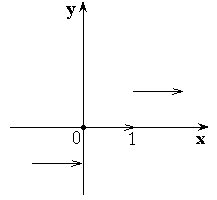
1. 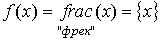 – дробная часть от числа x.
– дробная часть от числа x. 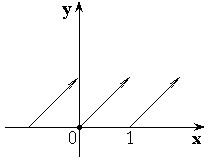
II. Если 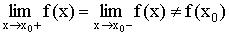 , то в точке
, то в точке 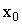 функция испытывает устранимый разрыв первого рода.
функция испытывает устранимый разрыв первого рода.
Примеры:
1) 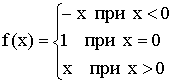

2) 
3) 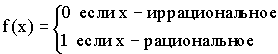
4) 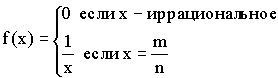
Разрыв второго рода
Функция испытывает разрыв второго рода, если 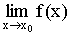 – не существует.
– не существует.
Свойства функции, непрерывной на замкнутом отрезке
Пусть функция 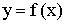 непрерывна на замкнутом отрезке
непрерывна на замкнутом отрезке  .
.
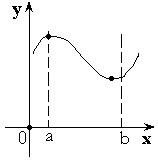 Теорема 1. Функция принимает наибольшее и наименьшее значение на
Теорема 1. Функция принимает наибольшее и наименьшее значение на  .
.
Или  , где
, где 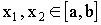 .
.
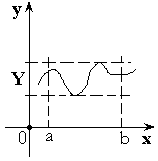 Теорема 2. Функция принимает все свои промежуточные
Теорема 2. Функция принимает все свои промежуточные
значения на  .
.
Или 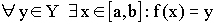 , где
, где  – область значений.
– область значений.
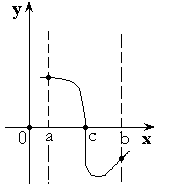 Теорема 3. Если функция принимает на концах отрезка
Теорема 3. Если функция принимает на концах отрезка  значения разных знаков, то внутри отрезка найдется точка, в которой
значения разных знаков, то внутри отрезка найдется точка, в которой 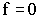 .
.
Или 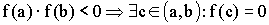 .
.
Исследование функции на непрерывность в точке проводится по уже накатанной рутинной схеме, которая состоит в проверке трёх условий непрерывности:
Задания для самостоятельного решения (домашнее задание)
Пример 3
Исследовать функцию 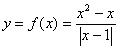 на непрерывность. Определить характер разрывов функции, если они существуют. Сделать чертёж.
на непрерывность. Определить характер разрывов функции, если они существуют. Сделать чертёж.
Пример 5
Исследовать функцию на непрерывность и построить её график 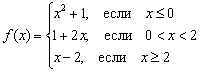 .
.
Пример 7
Дана функция 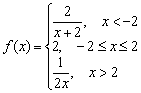 . Исследовать функцию на непрерывность в точках
. Исследовать функцию на непрерывность в точках 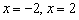 . Классифицировать точки разрыва, если они есть. Выполнить чертёж.
. Классифицировать точки разрыва, если они есть. Выполнить чертёж.
Пример 9
Исследовать на непрерывность функцию 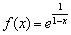 и выполнить схематический чертёж.
и выполнить схематический чертёж.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|