Хелпикс

Главная

Контакты

Случайная статья



Дисциплина: «Математика для экономистов»

Стр 1 из 2Следующая ⇒


 

Министерство образования и науки Республики Казахстан

ВОСТОЧНО КАЗАХСТАНСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА ИМЕНИ С. АМАНЖОЛОВА

ВЫСШИЙ КОЛЛЕДЖ

Дисциплина: «Математика для экономистов»

Специальность: « Учет и аудит» У-1А

Подготовила Курманова А. Б.

Лекция 06. 04. 20 г

Цель: Овладеть умениями и навыками исследования функций на непрерывность.

Тема: 2. Непрерывность функции в точке и на интервале

Определение 1.
Пусть функция 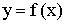определена в окрестности точки 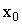, тогда функция непрерывна в 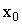, если .

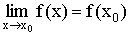Определение 2.
Функция 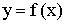непрерывна, если .

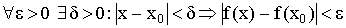Определение 3.
Функция 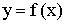непрерывна в точке 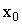, если . Приращение аргумента 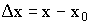. Приращение функции .

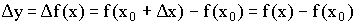Определение 4. Функция 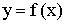непрерывна в точке 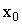, если 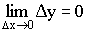. Если функция не является непрерывной в точке 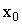, то эта точка – точка разрыва. Если функция непрерывна на отрезке (a, b), то функция неразрывна на отрезке (a, b).

Определение 5.
Функция 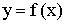непрерывна в точке 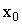справа, если .

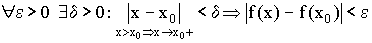Определение 6.
Функция 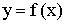непрерывна в точке 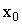слева, если .

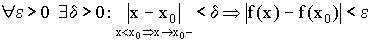Функция непрерывна на отрезке , если она непрерывна в каждой внутренней точке этого отрезка и односторонне непрерывна на его концах.

Теоремы о непрерывных функциях

Теорема 1. Сумма, произведение и частное непрерывных функций – непрерывны (кроме случая, когда знаменатель обращается в нуль).

Доказательство:

Пусть 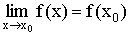и .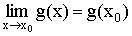

Тогда .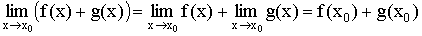

Доказательство для умножения и деления аналогично доказательству для сложения.

Теорема 2. Композиция непрерывных функций непрерывна:

Функция непрерывна в точке 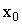, если g(x) непрерывна в точке 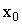и f(y) непрерывна в .

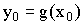Теорема 3. Все элементарные функции непрерывны в своей области определения.


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.