Достаточное условие вогнутости (выпуклости) функции.

Пусть функция f ( x ) дважды дифференцируема (имеет вторую производную) на интервале ( a, b ), тогда:

1) если f '' ( x ) > 0 для любого x 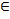( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );

2) если f '' ( x ) < 0 для любого x 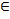( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ).

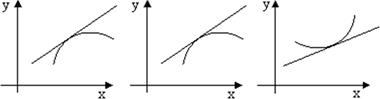
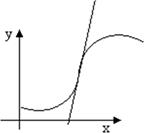
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0.

Правило нахождения точек перегиба графика функции y=f(x)

1) Найти вторую производную f″.

2) Найти точки, в которых вторая производная f″ обращается в нуль или терпит разрыв.

3) Исследовать знак второй производной f″ на каждом промежутке, на которые найденные критические точки делят область определения функции f(x). Если при этом критическая точка x₀ разделяет промежутки выпуклости противоположных направлений, то x₀ является абсциссой точки перегиба графика функции.

4) Вычислить значения функции в точках перегиба.

Пример: Найти промежутки выпуклости и точки перегиба функции f(x)=6x2-x3. Решение:

1. Находим f ′ (x)=(6x2-x3)′ = 12x-3x2, f ″ (x)=(12x-3x2)′ = 12-6x.

2. Найдем критические точки по второй производной, решив уравнение: 12-6x=0, x=2

4. f (2)=6·22-23=16

Ответ: Функция выпукла вверх при x∈ (2; +∞ ); функция выпукла вниз при x 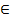(-∞; 2); точка перегиба (2; 16).

⇐ Предыдущая 123 Следующая ⇒