Тема: Вторая производная, ее геометрический и физический смысл. Применение производной к исследованию функций и построению графиков.

Урок-лекция

Цель: познакомиться с понятием второй производной функции и её применением в физике и в исследовании функции.

Задание: изучить материал урока, выполнить самостоятельную работу и домашнее задание.

Лекция

1. Если производная f ' ( x ) функции f ( x ) дифференцируема в точке x0, то её производная называется второй производной функции f ( x ) в точке x0, и обозначается f '' ( x0 ). Вторая производная - это производная от первой производной.

Пример: Найти производную второго порядка функции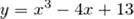

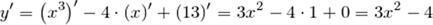Решение

Тогда искомая вторая производная:

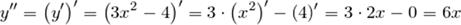
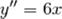Ответ:

Физический смысл производной второго порядка :

Пусть тело движется прямолинейно по некоторому закону s. Тогда в торая производная от пути по времени есть ускорение прямолинейного движения в данный момент времени: a= s'' или a = v' =s''.

Пример. Прямолинейное движение точки совершается по закону: s = (t3 — 2) м.

Определить ускорение в момент t = 10 сек.

Решение. Ускорение а =s''.

а =((t3 — 2)')'= (3t2-0)' = 6t

Следовательно, a (10)= 6t = 6*10 = 60; a = 60 м/сек2.

Ответ: 60 м/сек2.

2. Вторая производная f" (x) имеет также важное значение в анализе и в геометрии; в самом деле, представляя собой скорость изменения наклона f (х) кривой y = f (x), вторая производная дает указание на то, как изогнута кривая.

Функция f (x) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f (x) в любой точке (x0, f (x0)), x0 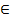(a, b).

Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f ( x ) в любой точке (x0, f (x0)), x0 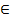(a, b).

12 3 Следующая ⇒