Уравнение равномерного прямолинейного движения точки.

Уравнение равномерного прямолинейного движения точки.

Пусть радиус-вектор 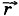₀ задаёт положение точки в начальный момент времени t₀, а радиус-вектор 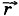— в момент времени t. Тогда Δ t = t — t₀, Δ 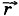= 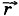- 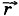₀, и выражение для скорости принимает вид:

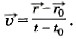
Если начальный момент времени t₀ принять равным нулю, то

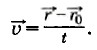
Отсюда

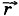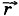= ₀ + 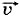t. (1)

Последнее уравнение и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий её положение в начальный момент времени.

Вместо векторного уравнения (1) можно записать три эквивалентных ему уравнения в проекциях на оси координат.

Радиус-вектор 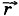является суммой двух векторов: радиус-вектора 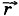₀ и вектора 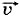t. Следовательно, проекции радиус-вектора 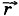на оси координат должны быть равны сумме проекций этих двух векторов на те же оси. Рассмотрим случай, когда направления 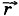₀ и 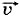совпадают.

х = х₀ + υ _xt. (1. 1)

Запомни Уравнение (1. 1) есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме.

⇐ Предыдущая 12