Равномерное прямолинейное движение. Скорость. Уравнение движения

Равномерное прямолинейное движение. Скорость. Уравнение движения

Движение точки называется равномерным, если она за любые равные промежутки времени проходит одинаковые пути.

Равномерное движение может быть как криволинейным, так и прямолинейным.

Скорость.

В механике рассматривают скорость как векторную величину. А это означает, что скорость можно считать 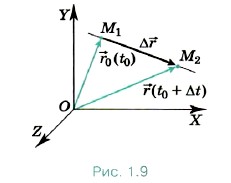известной (заданной) лишь в том случае, если известны её модуль и направление.

Пусть точка, двигаясь равномерно и прямолинейно в течение промежутка времени Δ t, переходит из положения М₁ в положение М₂, совершив при этом перемещение Δ 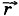. Поделим перемещение Δ 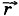на промежуток времени Δ t, в течение которого это перемещение произошло. В результате получим вектор.

(При делении вектора на число получаем вектор. ) Этот вектор называют скоростью равномерного прямолинейного движения точки и обозначают буквой 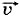. Следовательно, можно записать:

Так как промежуток времени Δ t — величина положительная, то скорость направлена так же, как и перемещение Δ 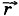. Выясним смысл модуля скорости

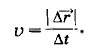
Запомни Скоростью равномерного прямолинейного движения точки называется векторная величина, равная отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло.

12 Следующая ⇒