1.1.1. Эмпирический Байесовский подход при решении скоринговых задач.

А) Каждый заемщик характеризуется пятью параметрами

В₁- пол. М(0), Ж(1)

В₂– сем. пол. В браке(1), холост (0)

В₃– возраст. 18-29(1), 30-45(2), 46 и выше(0)

В₄- % по кредиту от дохода заемщика, выплачиваемый ежемесячно. 5-10% (3), 10-20% (2), 21-50% (1), 51-60% (0).

В₅– дети. Есть(1), нет(0)

Б) Образуем новые множества 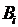, как комбинацию всех возможных свойств клиента - 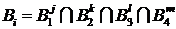. Количество таких множеств в нашем случае равно 96. (см. табл. “Кадировка множеств” в EXCEL). Таким образом, у нас получается 96 групп заемщиков.

В) У нас имеется выборка 1999 значений, распределенная таким образом как показано в табл. 2. «Количество по группам» (столбец B)

(Количество клиентов вернувших и не вернувших кредит в каждой группе. 0 – вернули кредит, 1 – не вернули кредит)

Г) Построим совместное эмпирическое распределение вероятностей. Для этого разделим количество клиентов вернувших и не вернувших кредит в каждой из групп на общее количество клиентов. табл. 2. «Количество по группам» (столбец С).

Д) Найдём эмпирическое распределение вероятностей попадания в каждую из групп. Для этого разделим количество клиентов в каждой группе на общее количество клиентов. Общее количество клиентов 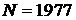. . 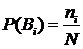(по факту мы это уже сделали в столбце С табл. 2. «Количество по группам», но для наглядности перейдем в табл. 3 «надежность опр. ранее»)

Е) Найдём рейтинги клиентов как эмпирическую вероятность того, что клиент вернёт кредит при условии, что он принадлежит какой-либо группе. ( в табл. 3 «надежность опр. ранее» =D/С)

Ё) И последнее, выделим 6 вариантов, как это предложено в столбце G табл. 3 «надежность опр. ранее».

	Начало интервала	Конец интервала
	0, 20	0, 33
	0, 33	0, 47
	0, 47	0, 60
	0, 6	0, 73
	0, 73	0, 87
	0, 87	1, 00

Как это должно быть…. Вводя критерии B1, B2 и т. д. на выходе должен появиться рейтинг заемщика и к какому варианту из 6 он относится.

Отлично мы построили наивный Байесовский классификатор.

12 Следующая ⇒