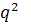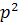- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Учитывая, что Р[(АС)(ВС)] = Р(АВС), окончательно получим P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC).
#79 Даны три попарно независимых события A, B, C, которые, однако, все три вместе произойти не могут. Предполагая, что все они имеют одну и ту же вероятность p, найти наибольшее возможное значение p.
Решение. Так как события попарно независимы и 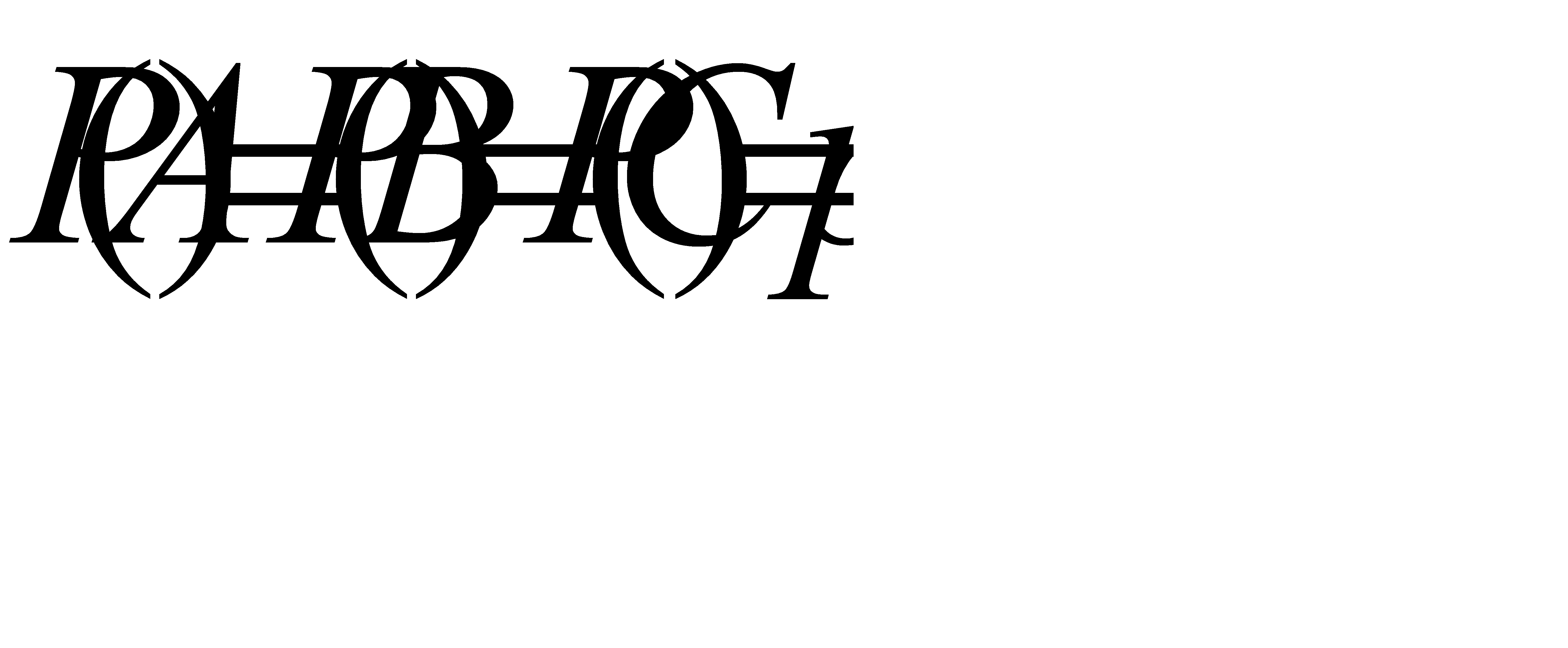 , также верно
, также верно 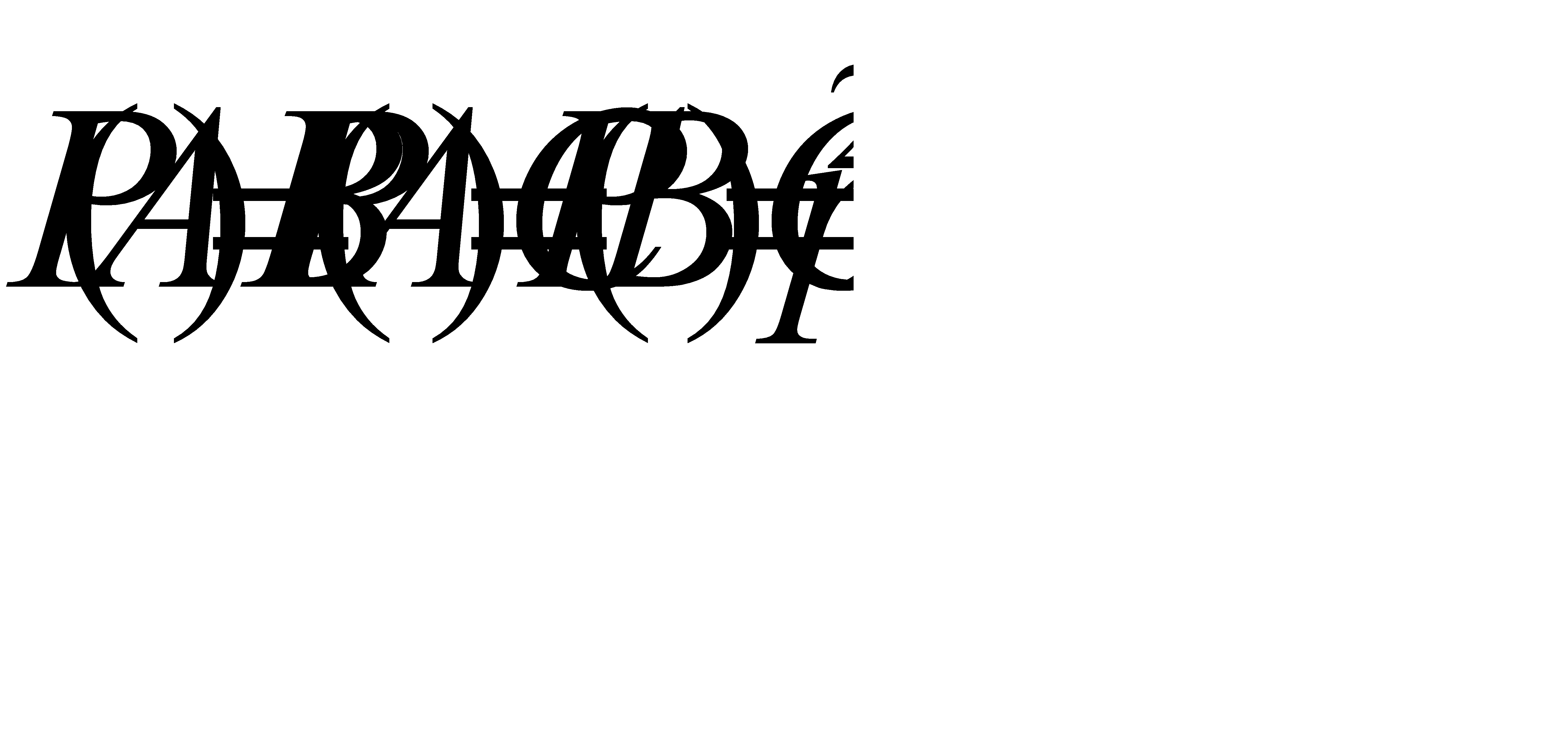 .
.
Обозначим 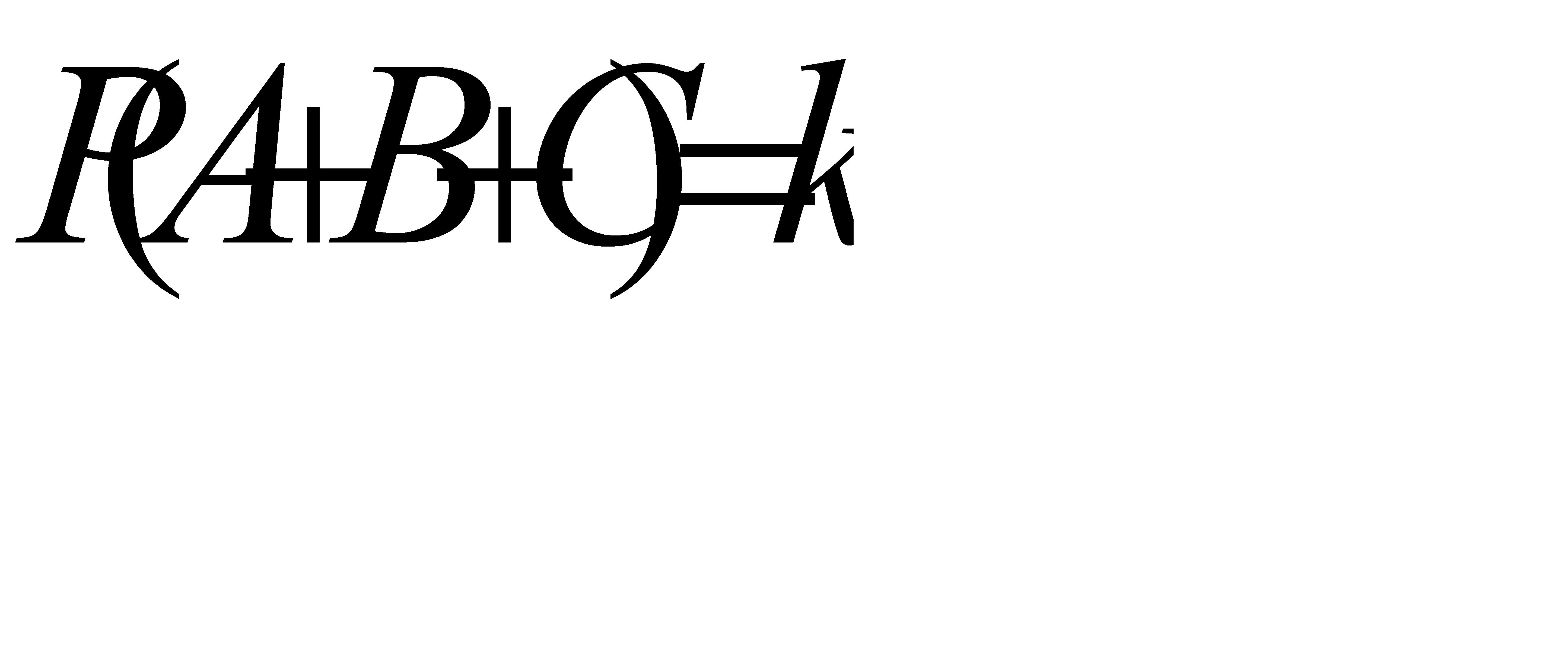 . Выразим
. Выразим 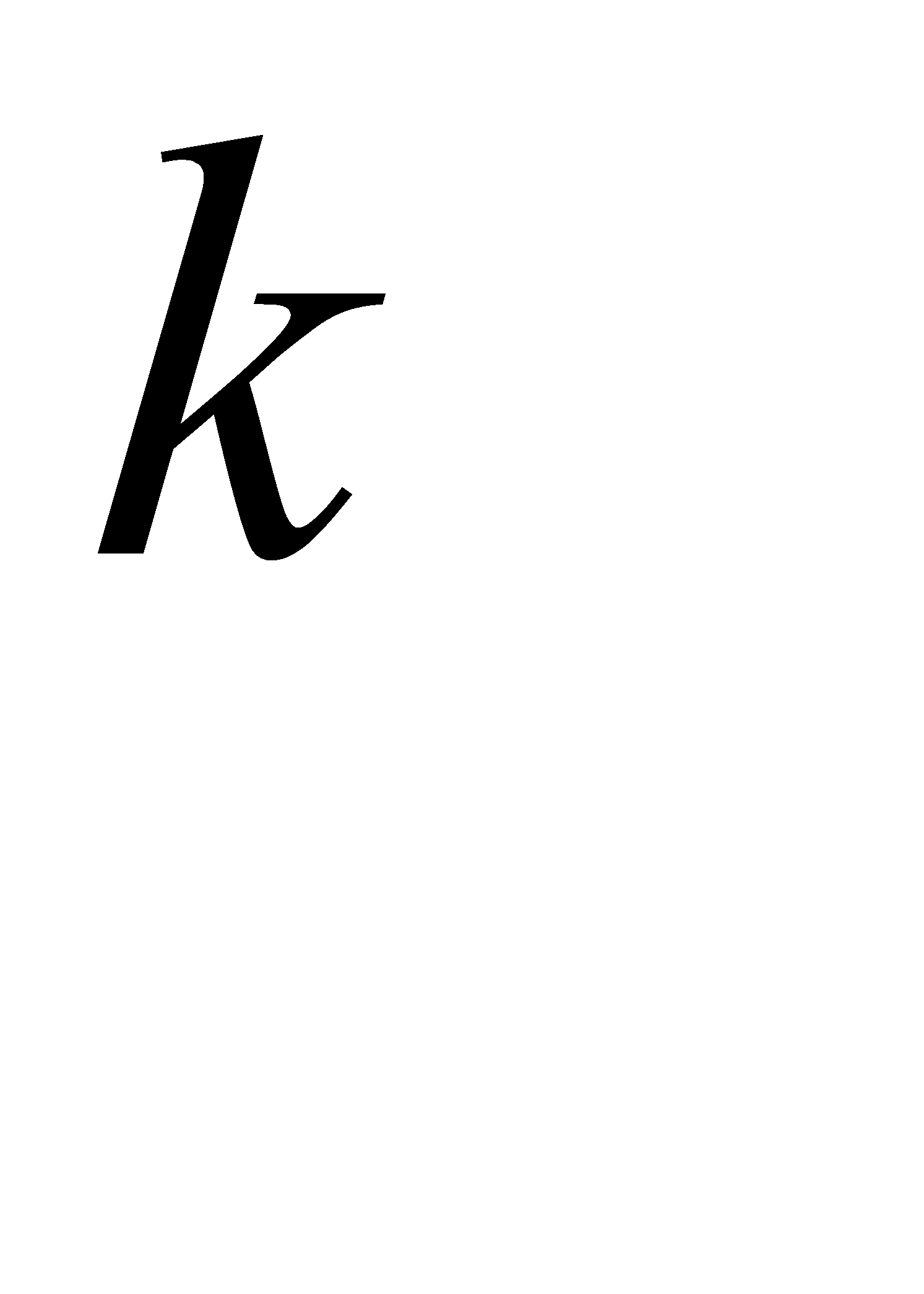 через
через 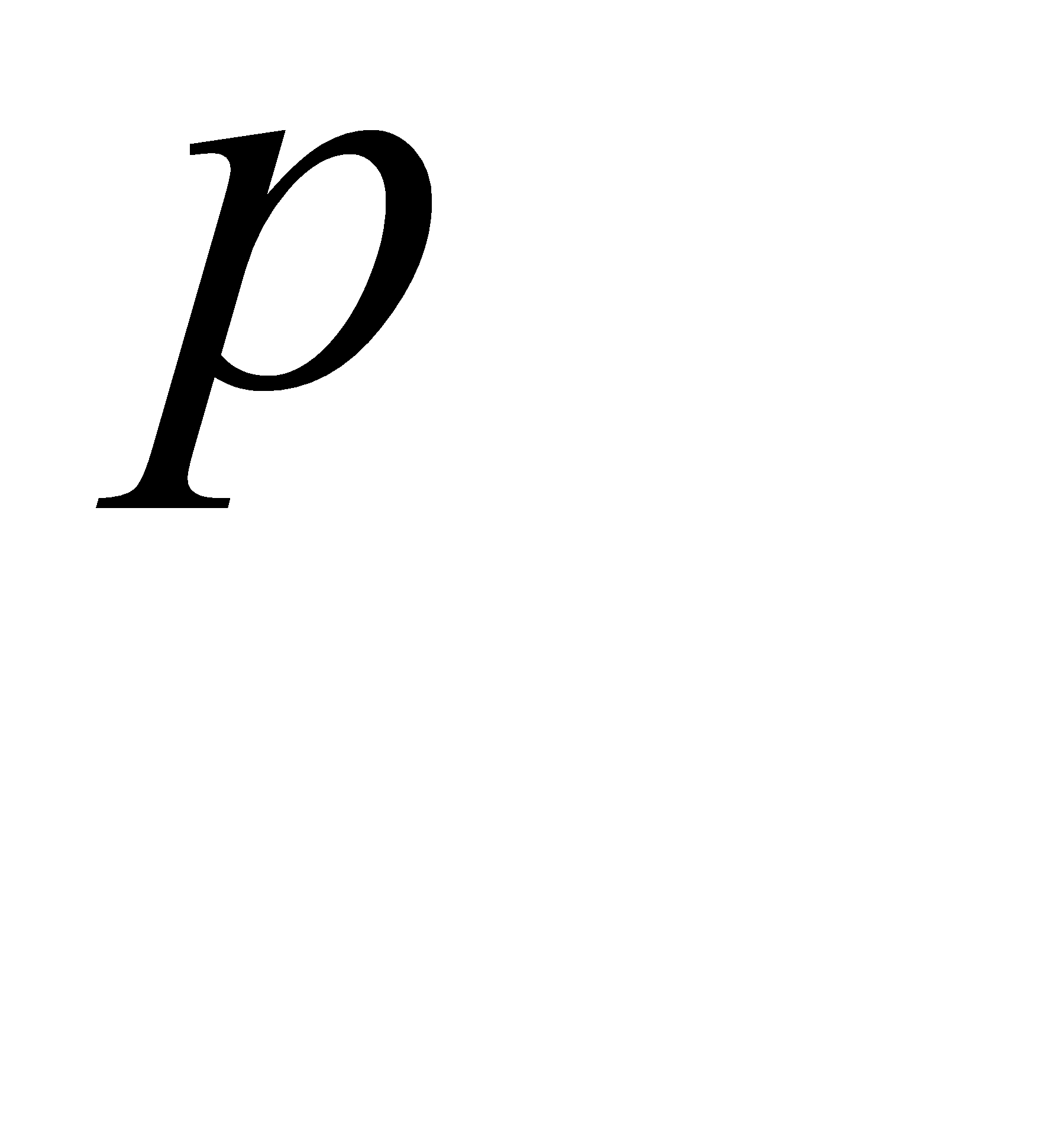 , пользуясь теоремой сложения для трёх несовместных событий:
, пользуясь теоремой сложения для трёх несовместных событий:
 .
.
Решив это уравнение относительно 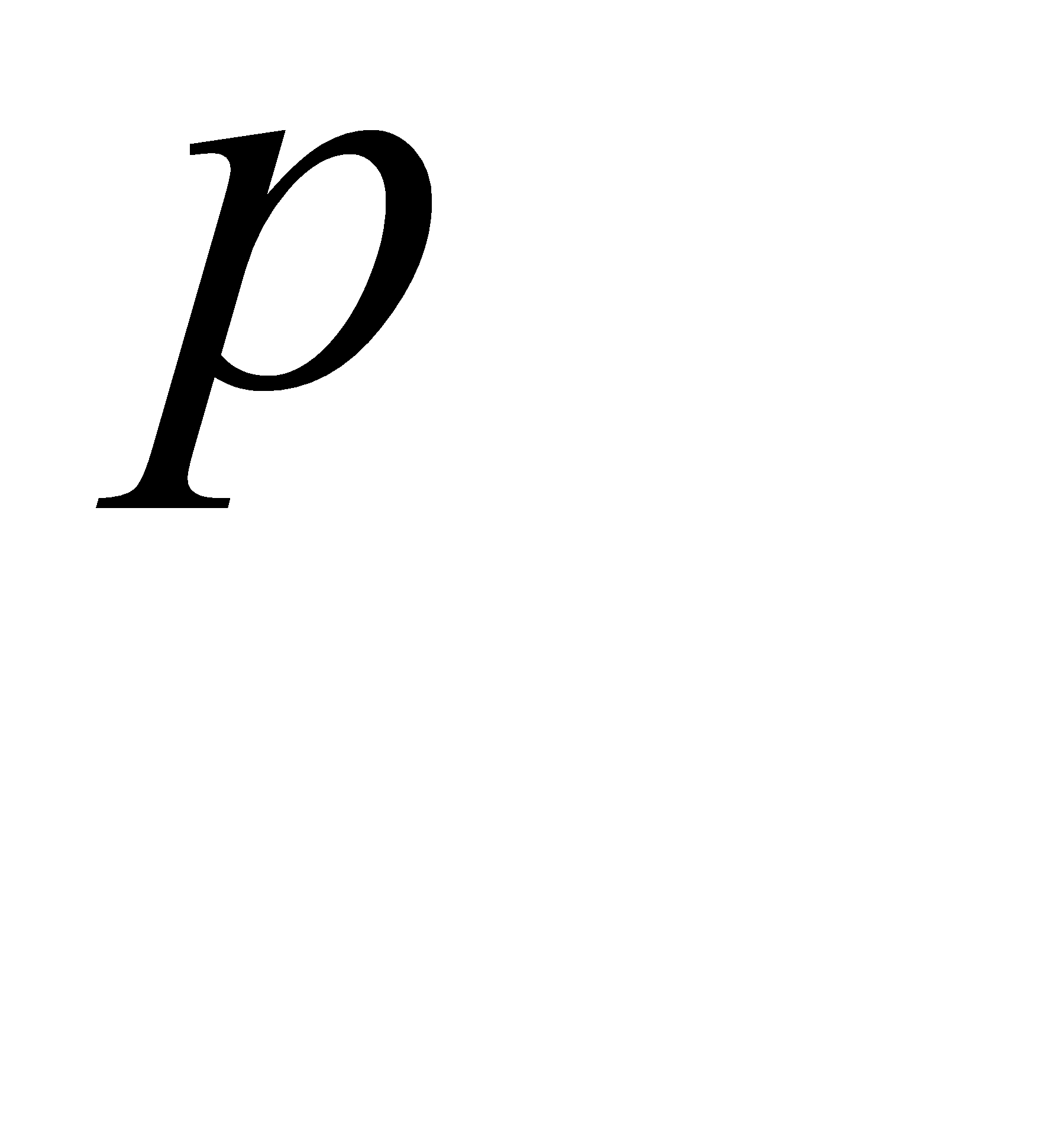 , получим
, получим 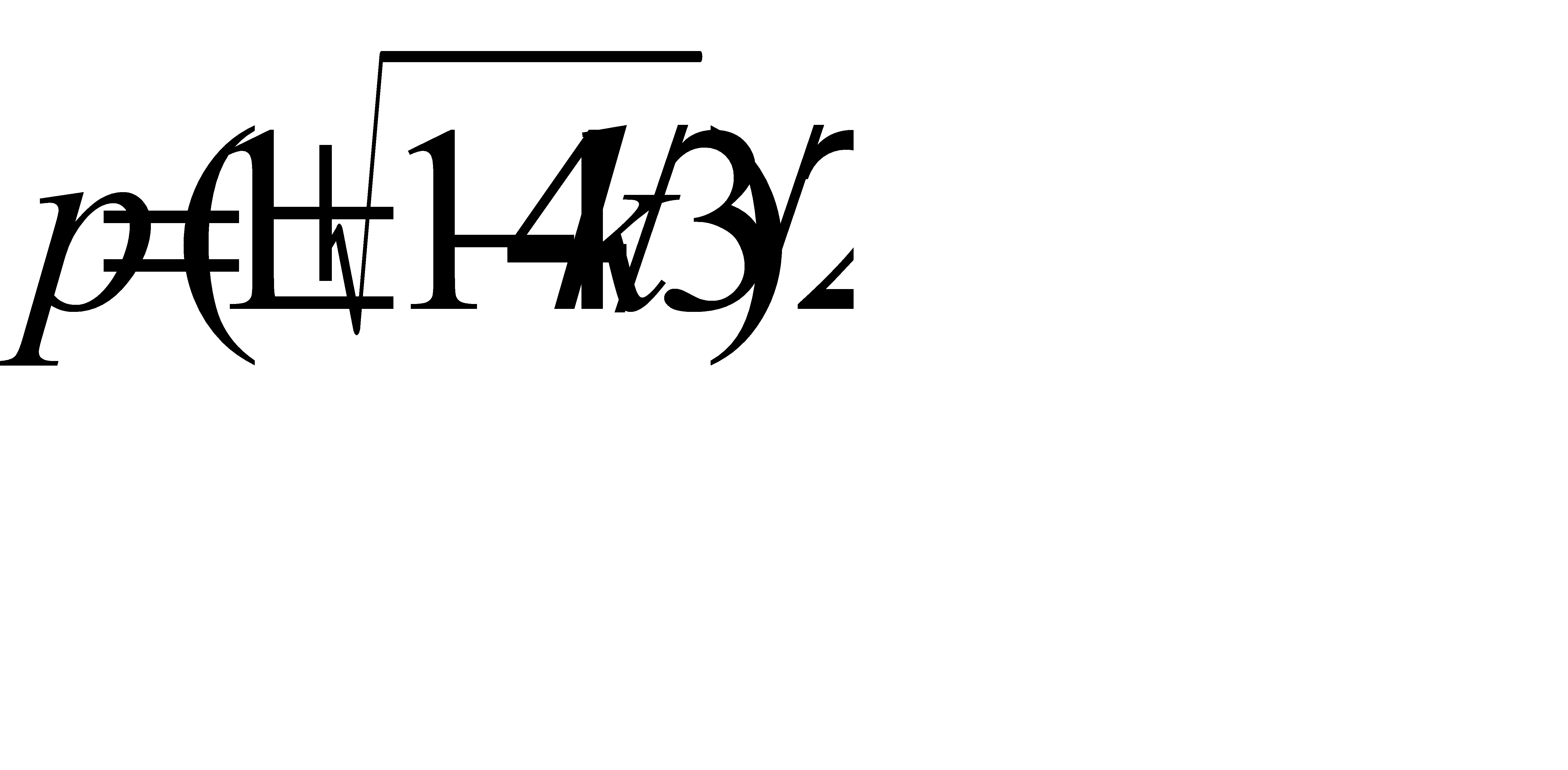 .
.
В таком случае 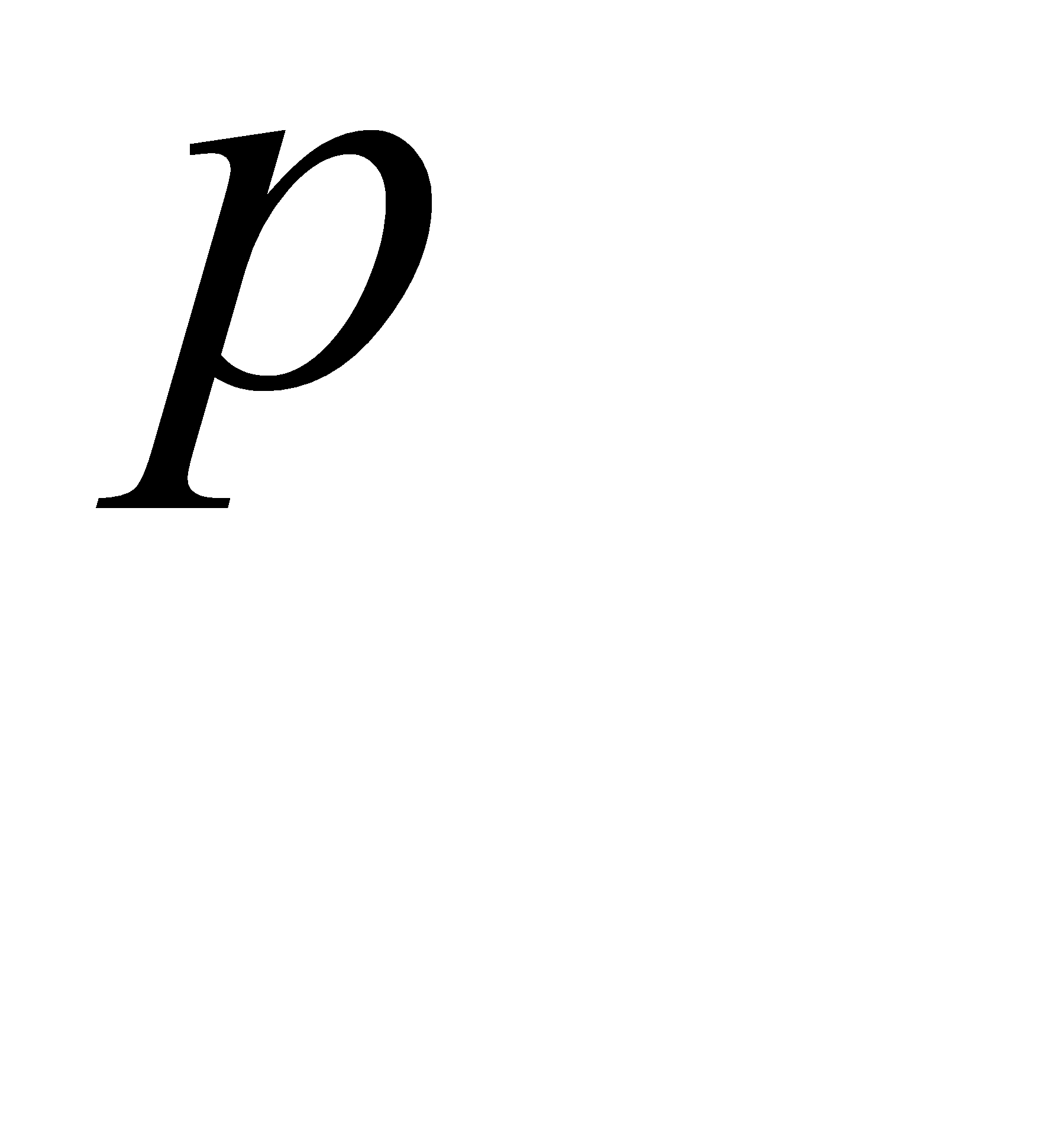 достигает максимального значения
достигает максимального значения 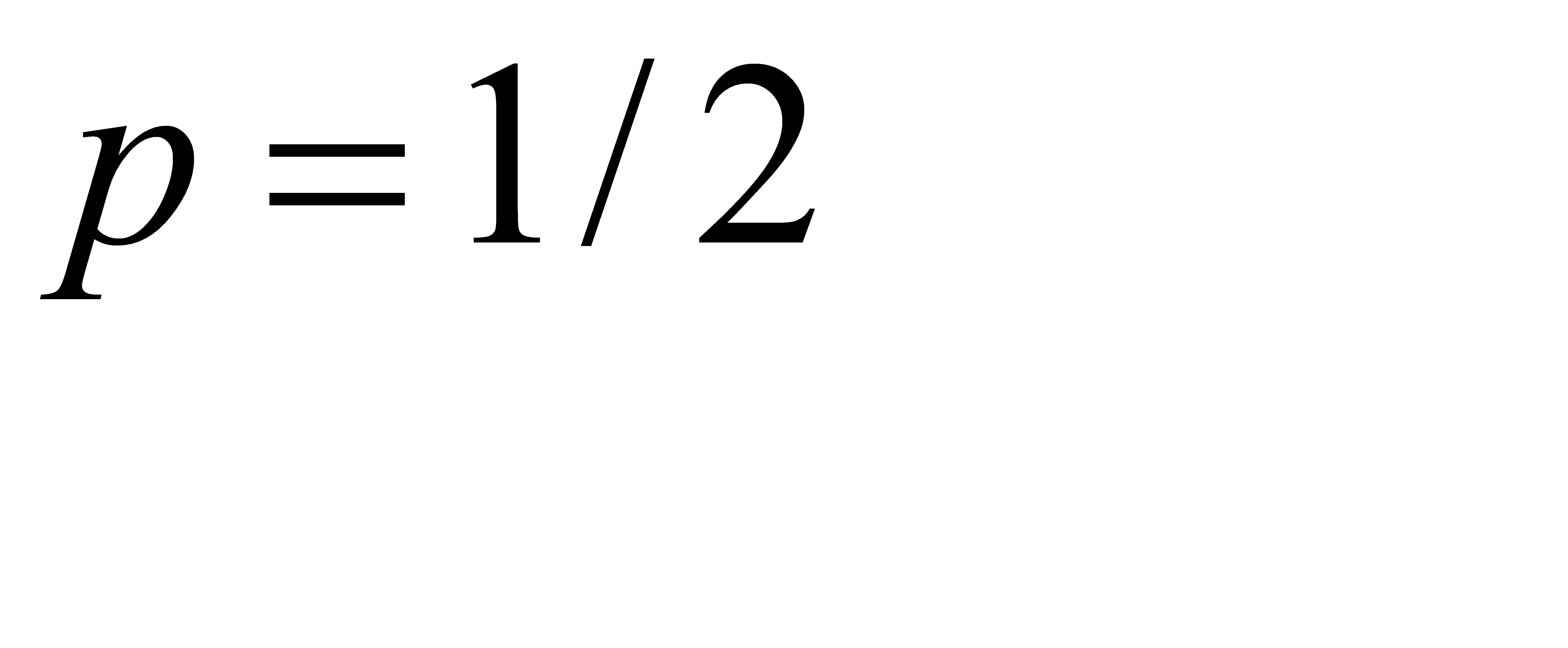 (при
(при  ).
).
Если 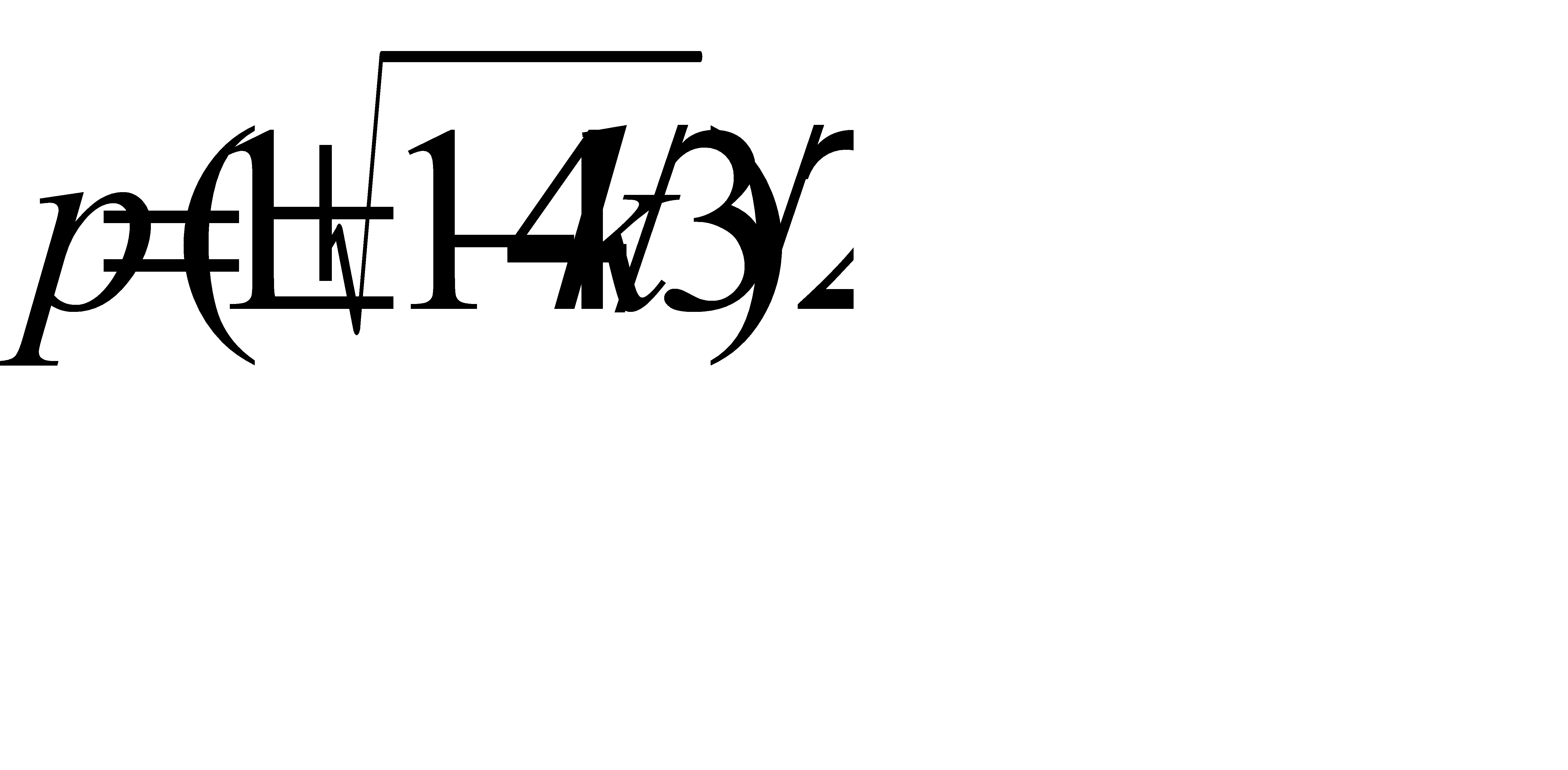 , то, на первый взгляд,
, то, на первый взгляд, 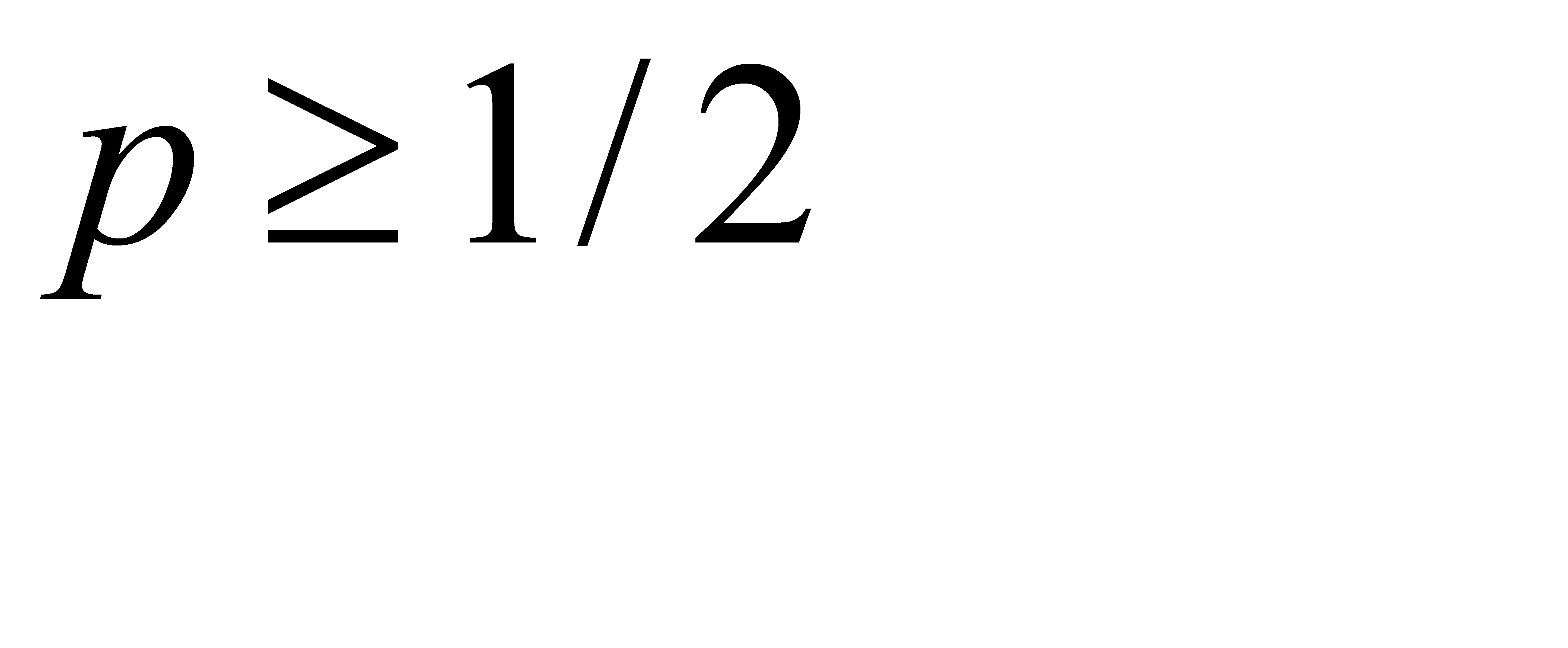 . Покажем, что допущение
. Покажем, что допущение 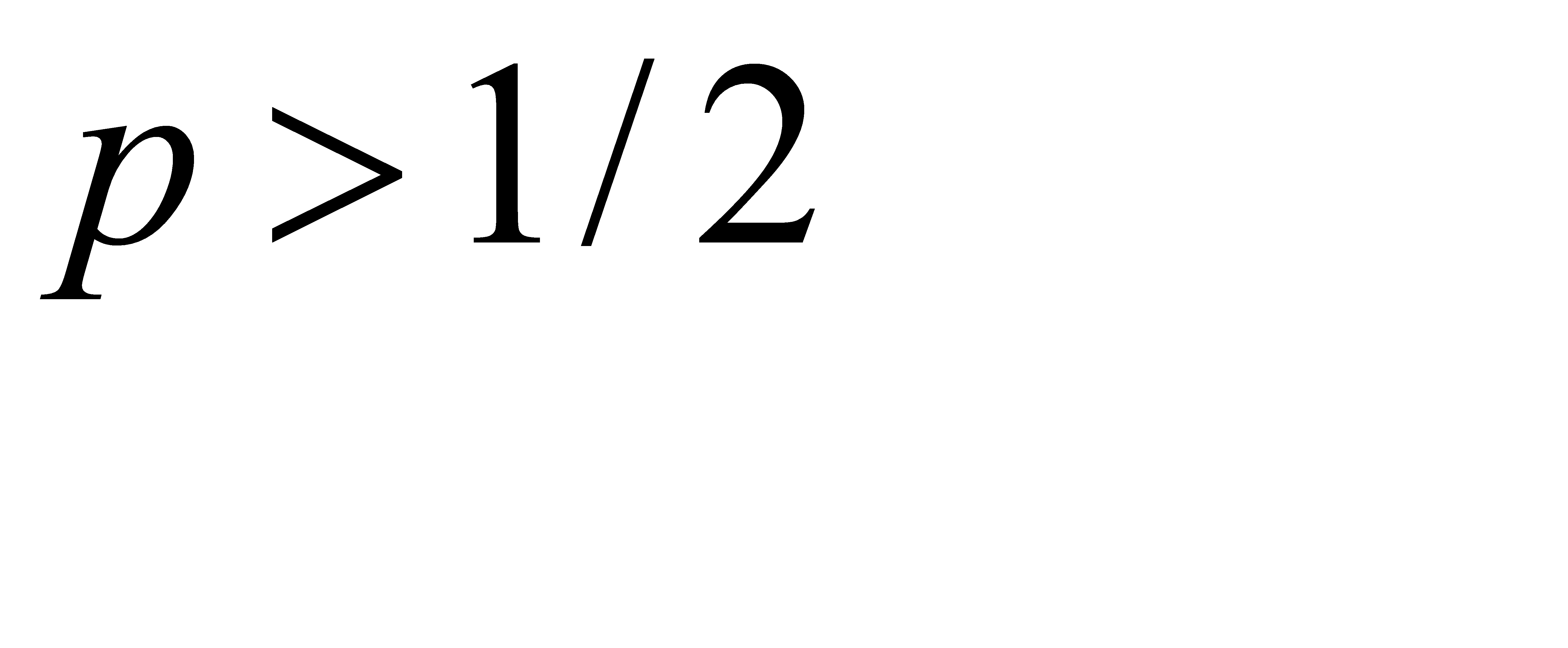 приводит к противоречию. Действительно,
приводит к противоречию. Действительно, 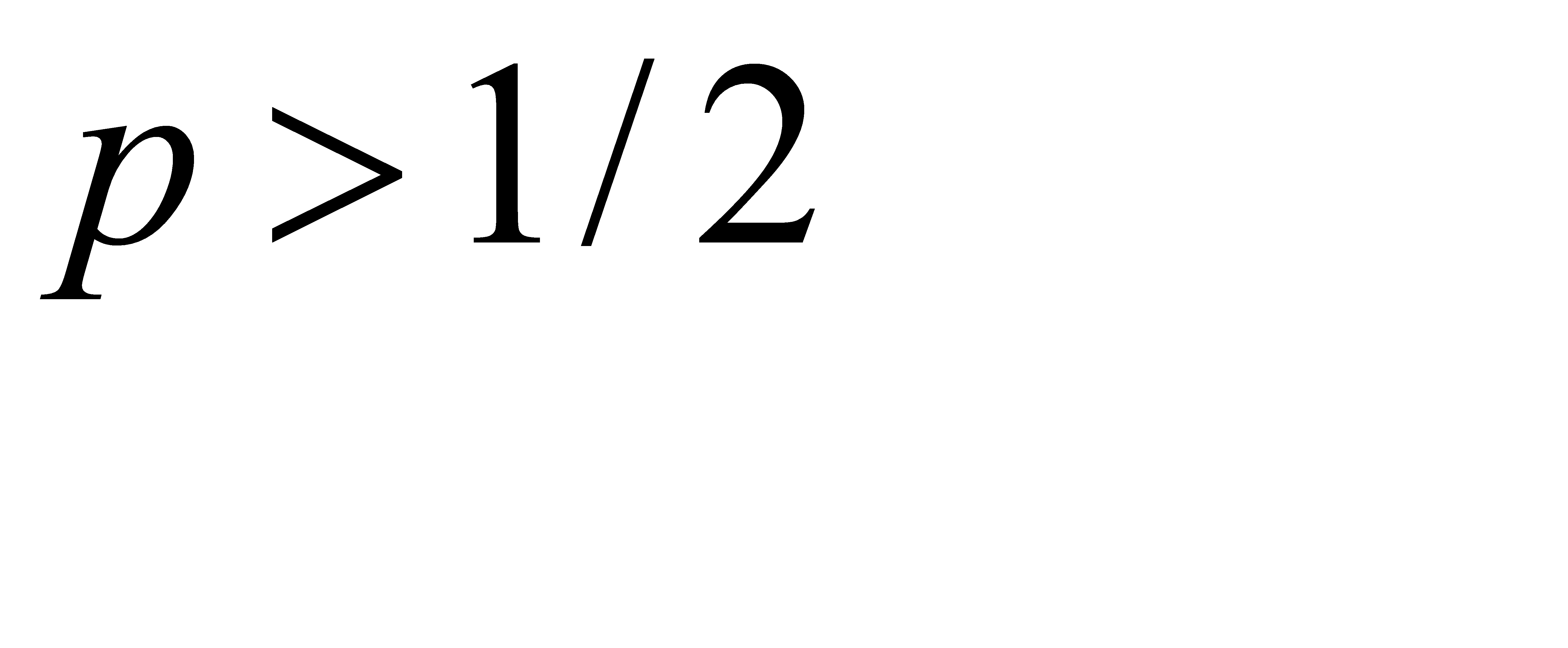 при условии, что
при условии, что 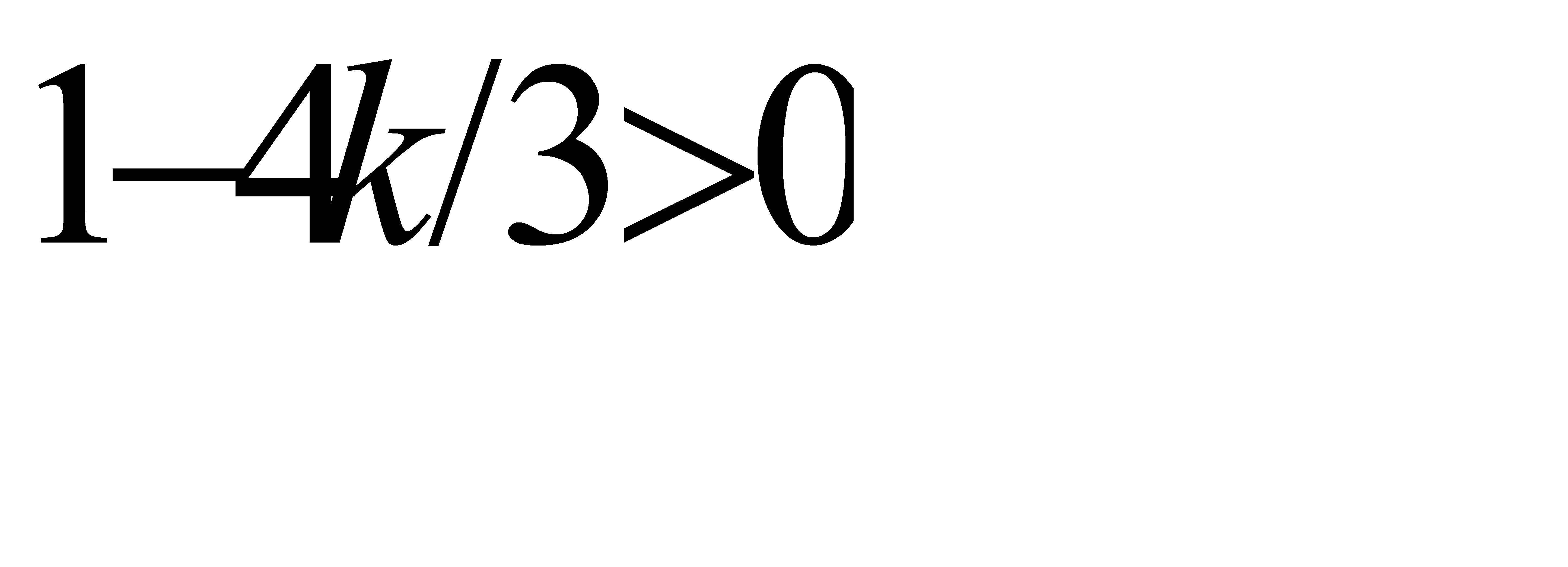 ; или, так как
; или, так как 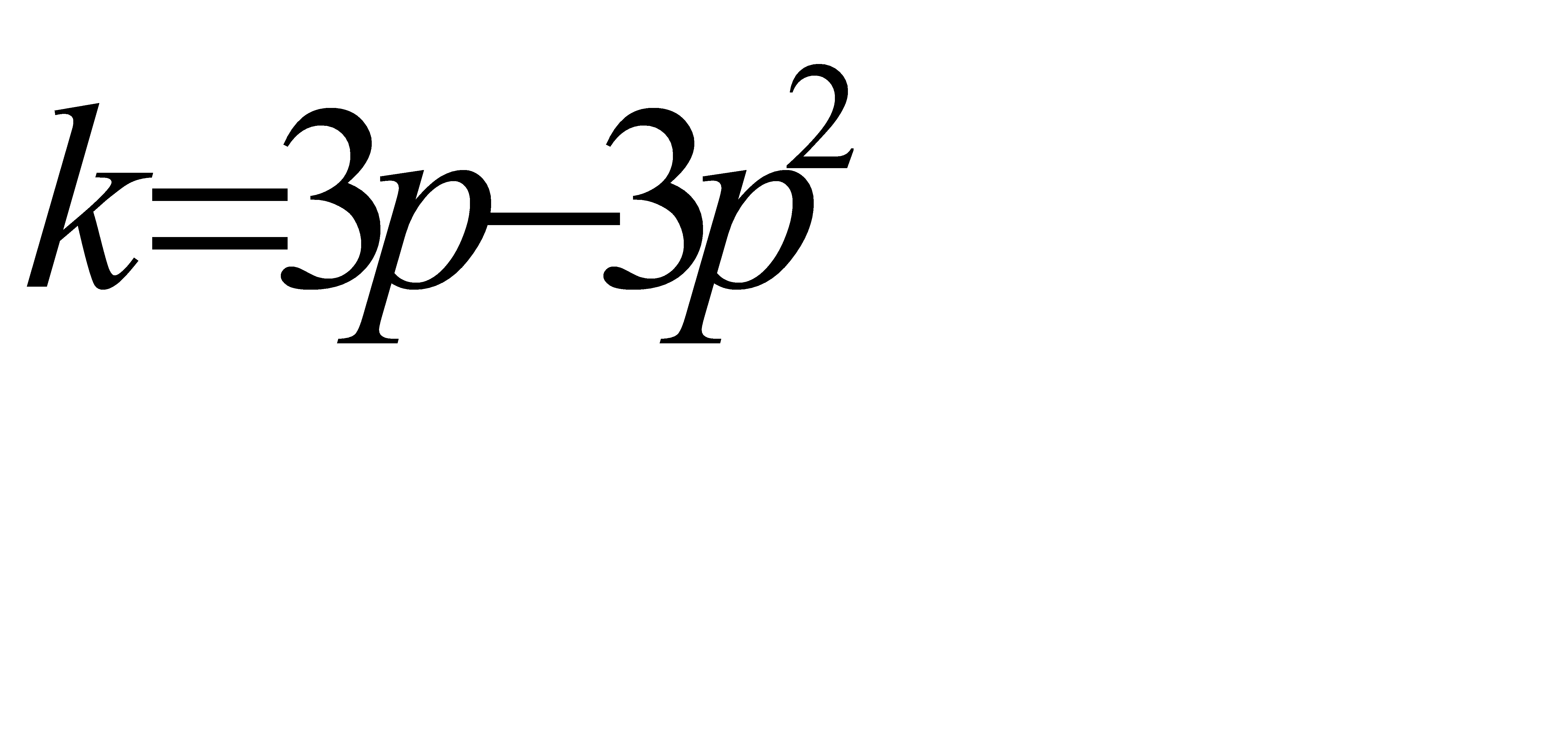 , при условии, что
, при условии, что 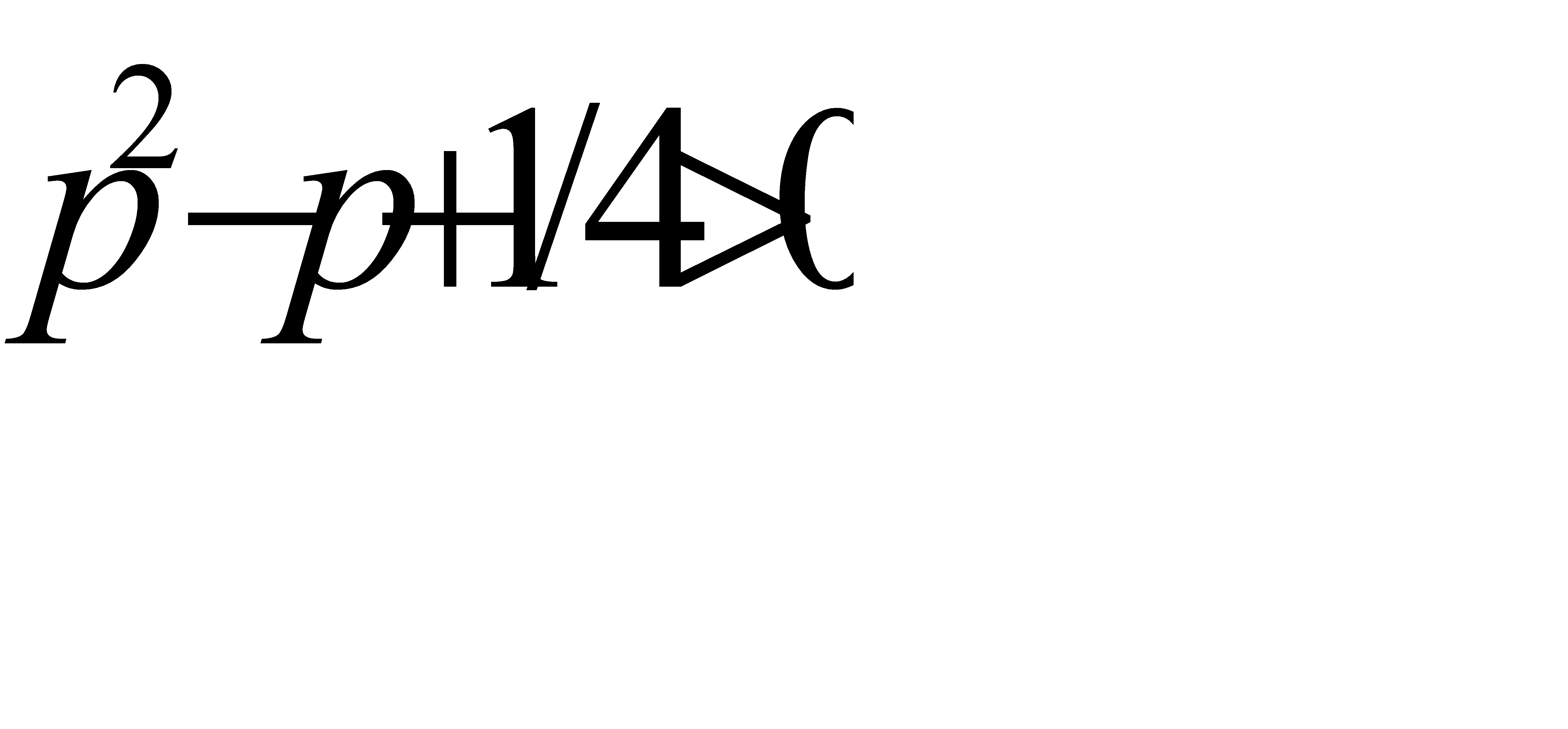 . Отсюда
. Отсюда  .
.
Итак, наибольшее возможное значение 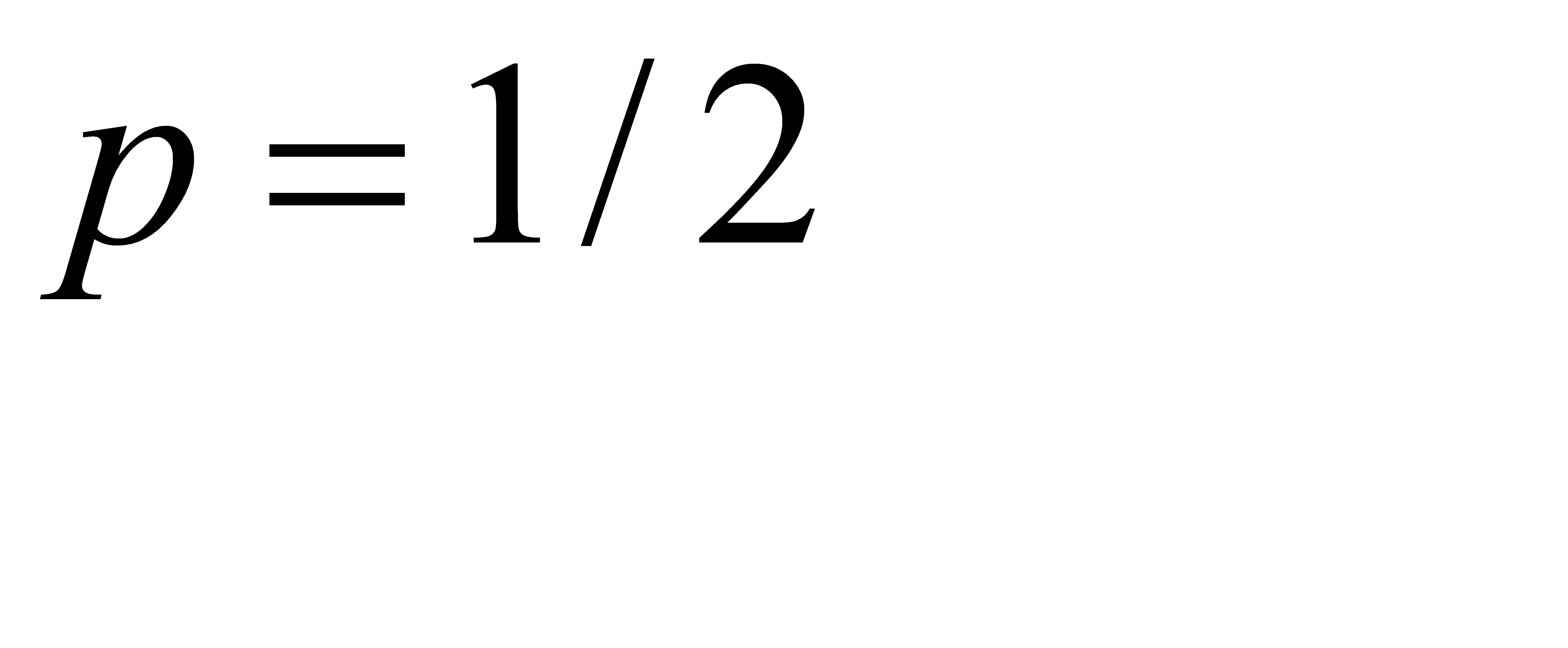 .
.
#80 Вероятность отказа первого элемента равна 0, 1, второго -
0, 15, третьего – 0, 2
То есть 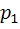 =0, 1,
=0, 1, 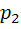 =0, 15,
=0, 15, 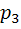 =0, 2
=0, 2
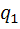 =0, 9,
=0, 9, 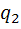 =0, 85,
=0, 85, 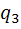 =0, 8
=0, 8
Тока в цепи не будет, если откажет хотя бы один элемент
То есть нужно использовать формулу появления хотя бы одного события (P(A)=1- 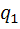 *…*
*…* 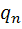 )
)
Значит, искомая вероятность равна 0, 388
(P(A)=1- 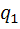 *
* 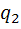 *
* 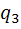 =1-(0, 9*0, 85*0, 8)=0, 388)
=1-(0, 9*0, 85*0, 8)=0, 388)
Ответ: 0, 388
#81 Решение: Вероятность того, что откажет 1й элемент, 2й элемент или оба, обратна вероятности того, что ни один не откажет, т. е.: 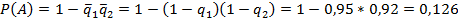 Ответ: 0, 126.
Ответ: 0, 126.
#82Решение: При последовательном сбрасывании четырех бомб мост будет разрушен (событие А), если в него попадет хотя бы одна бомба. Следовательно, искомая вероятность равна:
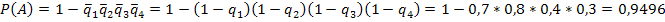
Ответ: 0, 9496.
#83 Решение. Вероятность того, что при однократном измерении хотя бы один из исследователей допустит ошибку равна:
Р(А) = 1 - q1q2q3 = 1 –(1 – 0, 1)*(1 – 0, 15)*(1 – 0, 2) = 0, 388.
#84Решение. Для вручения приза достаточно, чтобы хотя бы одна из четырех попыток была успешной. Вероятность успешной попытки р = 0, 5, а неуспешной q=1 - 0, 5 = 0, 5. Искомая вероятность Р = 1 - q^4 = 1 —0, 5^4 =0, 9375.
#85
Решение. Для получения приза достаточно, чтобы хотя бы одна из четырех попыток была успешна. Вероятность успешной попытки p=0, 3, неуспешной q=1-p=0, 7. Тогда искомая вероятность будет равна P=1-q*q*q*q=1- 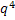 ≈ 0, 76
≈ 0, 76
#86Решение: Вероятность попадания в мишень хотя бы при одном из трех выстрелов (событие А) равна
Р(А)=1-q3, где q — вероятность промаха. По условию, P (A) = 0, 875. Следовательно,
0, 875=1—q3, или q3 = 1—0, 875 = 0, 125.
Отсюда q= 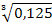 =0, 5. Искомая вероятность р = 1— q = 1—0, 5 = 0, 5.
=0, 5. Искомая вероятность р = 1— q = 1—0, 5 = 0, 5.
#87Решение: Вероятность попадания в мишень хотя бы при одном из трех выстрелов (событие А) равна
Р(А)=1-q4, где q — вероятность промаха. По условию, P (A) = 0, 9984. Следовательно,
0, 9984=1—q4, или q4 = 1—0, 9984= 0, 0016.
Отсюда q= 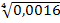 =0, 2. Искомая вероятность р = 1— q = 1—0, 2 = 0, 8.
=0, 2. Искомая вероятность р = 1— q = 1—0, 2 = 0, 8.
#88Решение: Вероятность хотя бы одной ошибки из 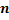 считываний равна
считываний равна 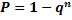 , где
, где 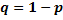 , и
, и 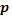 - вероятность ошибки при одном считывании. Из условия
- вероятность ошибки при одном считывании. Из условия 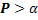 получим:
получим:
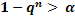 ;
; 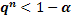 ;
; 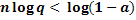 ;
; 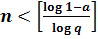
Следовательно, искомое число измерений равно 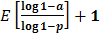 , где
, где 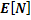 – целая часть числа
– целая часть числа 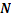
#89Решение: Обозначим через А событие - извлечен белый шар. Возможны следующие предположения о первоначальном составе шаров: В1 - белых шаров нет, В2 - один белый шар, В3 - два белых шара. Поскольку всего имеется три гипотезы, причем по условию они равновероятны, и сумма вероятностей гипотез равна единице (так как они образуют полную группу событий), то вероятность каждой из гипотез равна 1/3, т. е. P(B1) = P(B2) = P(B3) = 
Вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне не было белых шаров, 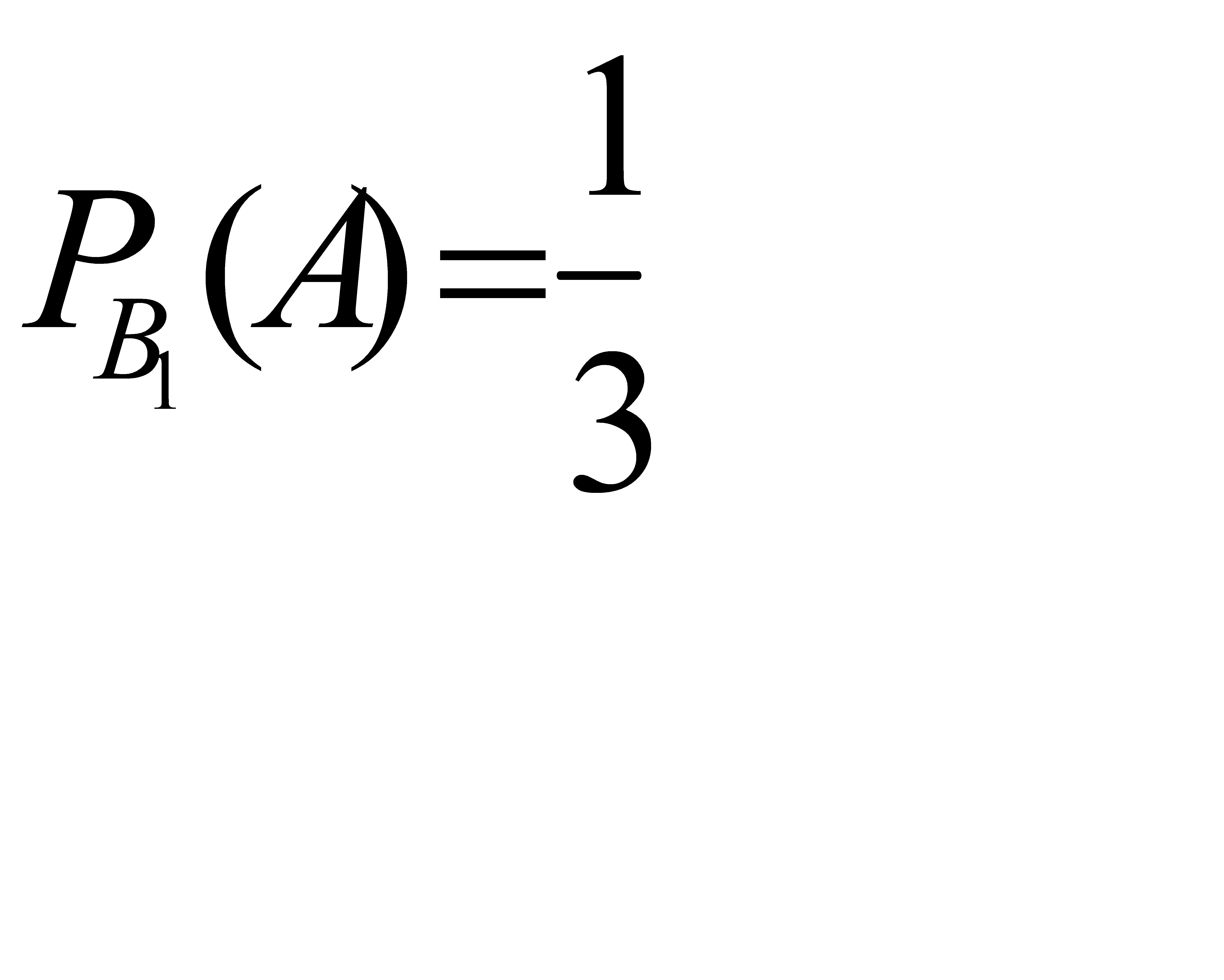 . Если в урне был один белый шар, то
. Если в урне был один белый шар, то 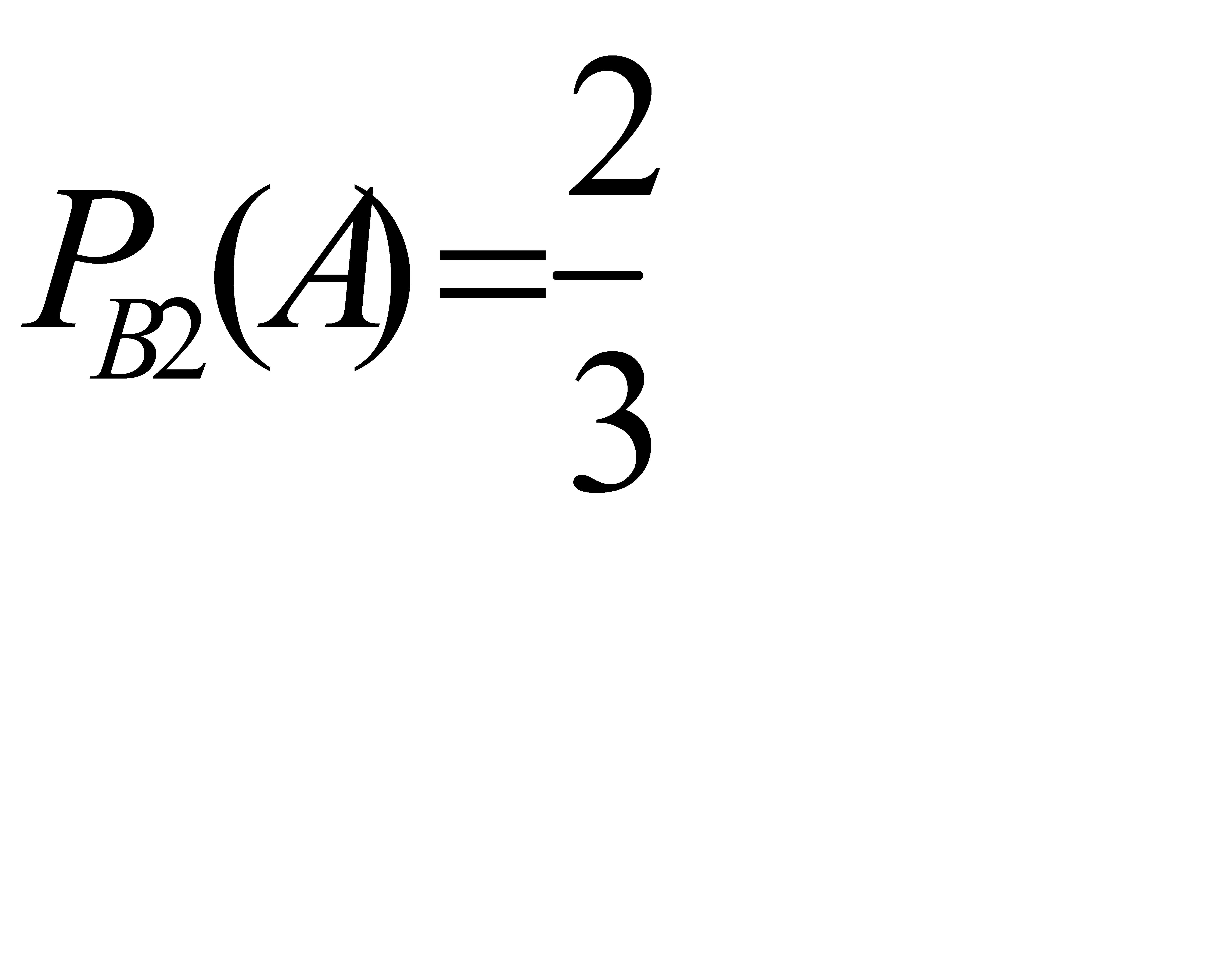 . Условная вероятность того, что будет извлечен белый шар, при условии, что в урне было два белых шара
. Условная вероятность того, что будет извлечен белый шар, при условии, что в урне было два белых шара 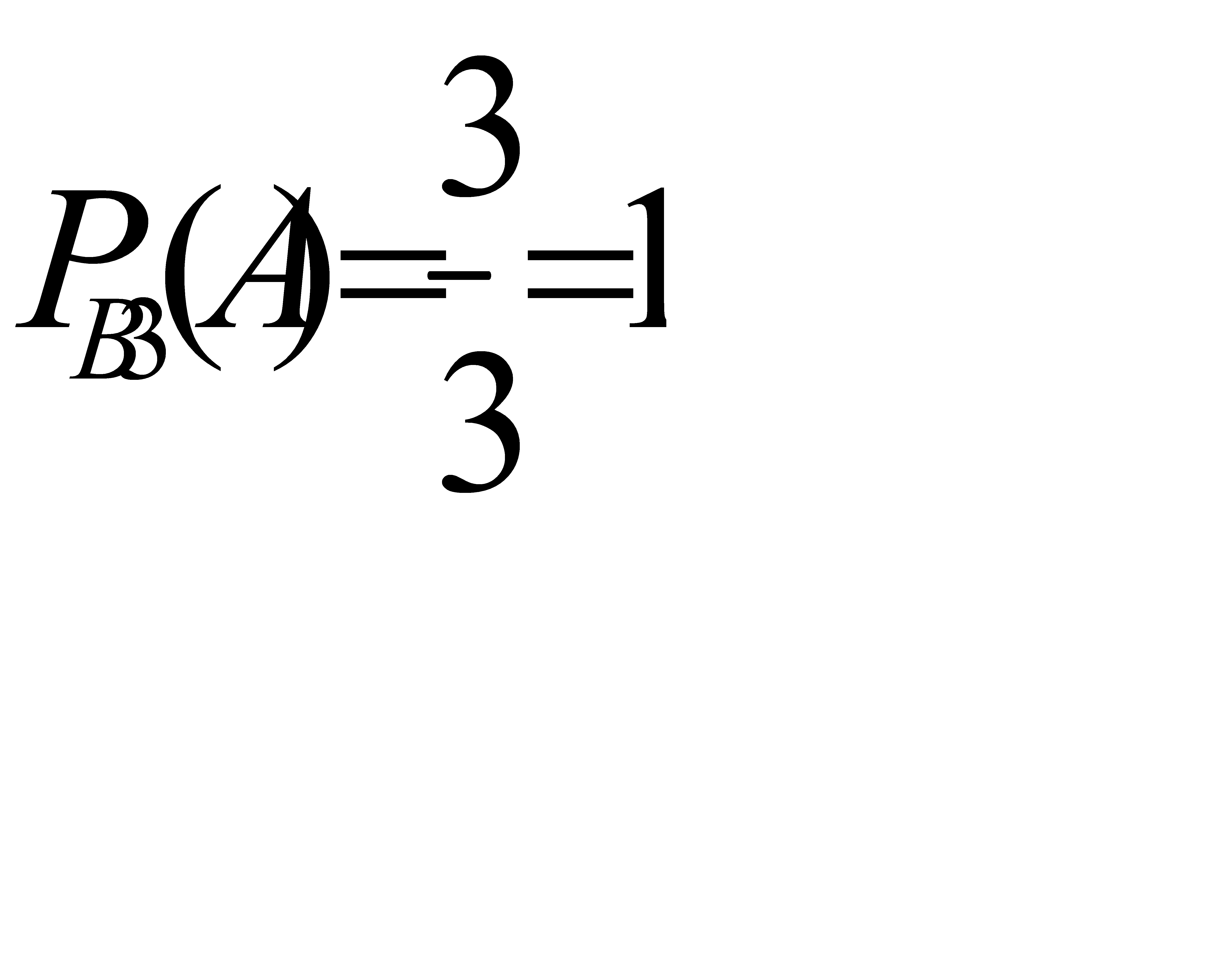 Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:
Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:
 Ответ: P(A)=
Ответ: P(A)= 
#90
Решение: Обозначим через А событие - извлечен белый шар. Возможны следующие предположения о первоначальном составе шаров: В1- 1 белый шар, В2- 2 белых шара... Вn-n белых шаров. Поскольку всего имеется n гипотез, причем по условию они равновозможны и сумма вероятностей равна единице, то вероятность каждой гипотезы равна  . По гипотезе В1 условная вероятность вытащить белый шар равна
. По гипотезе В1 условная вероятность вытащить белый шар равна 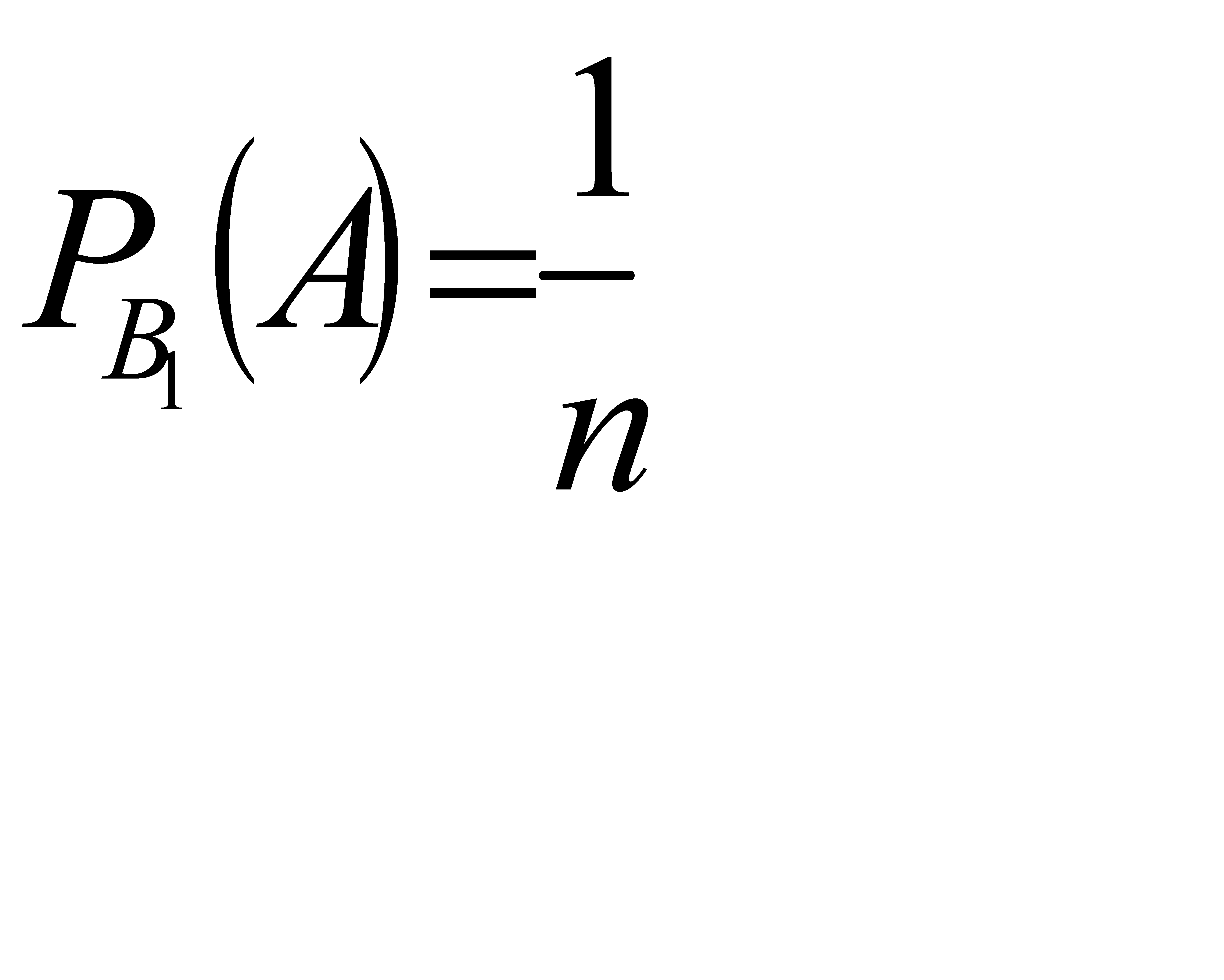 , по гипотезе В2 условная вероятность вытащить белый шар равна
, по гипотезе В2 условная вероятность вытащить белый шар равна 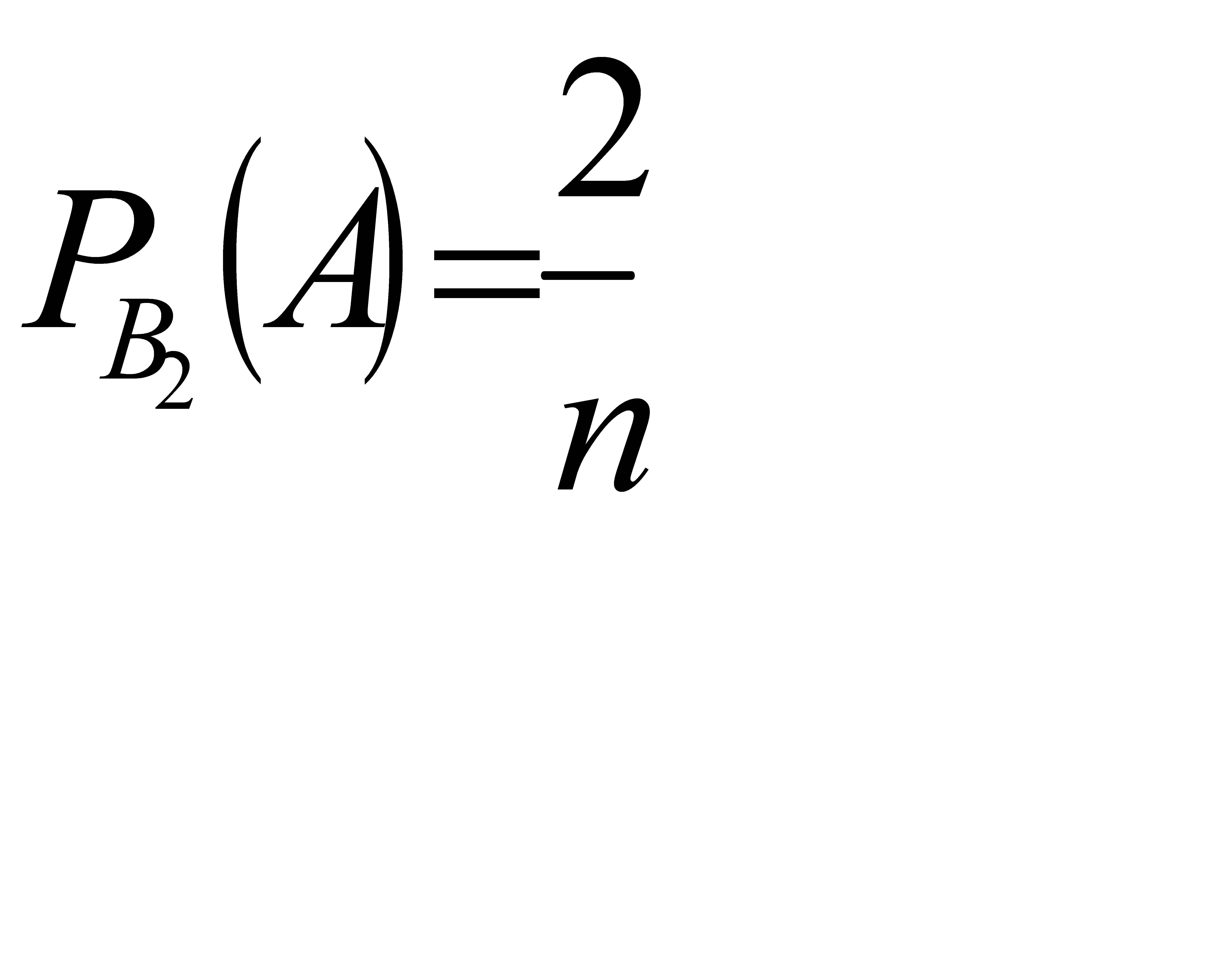 … по гипотезе Вn условная вероятность вытащить белый шар равна
… по гипотезе Вn условная вероятность вытащить белый шар равна 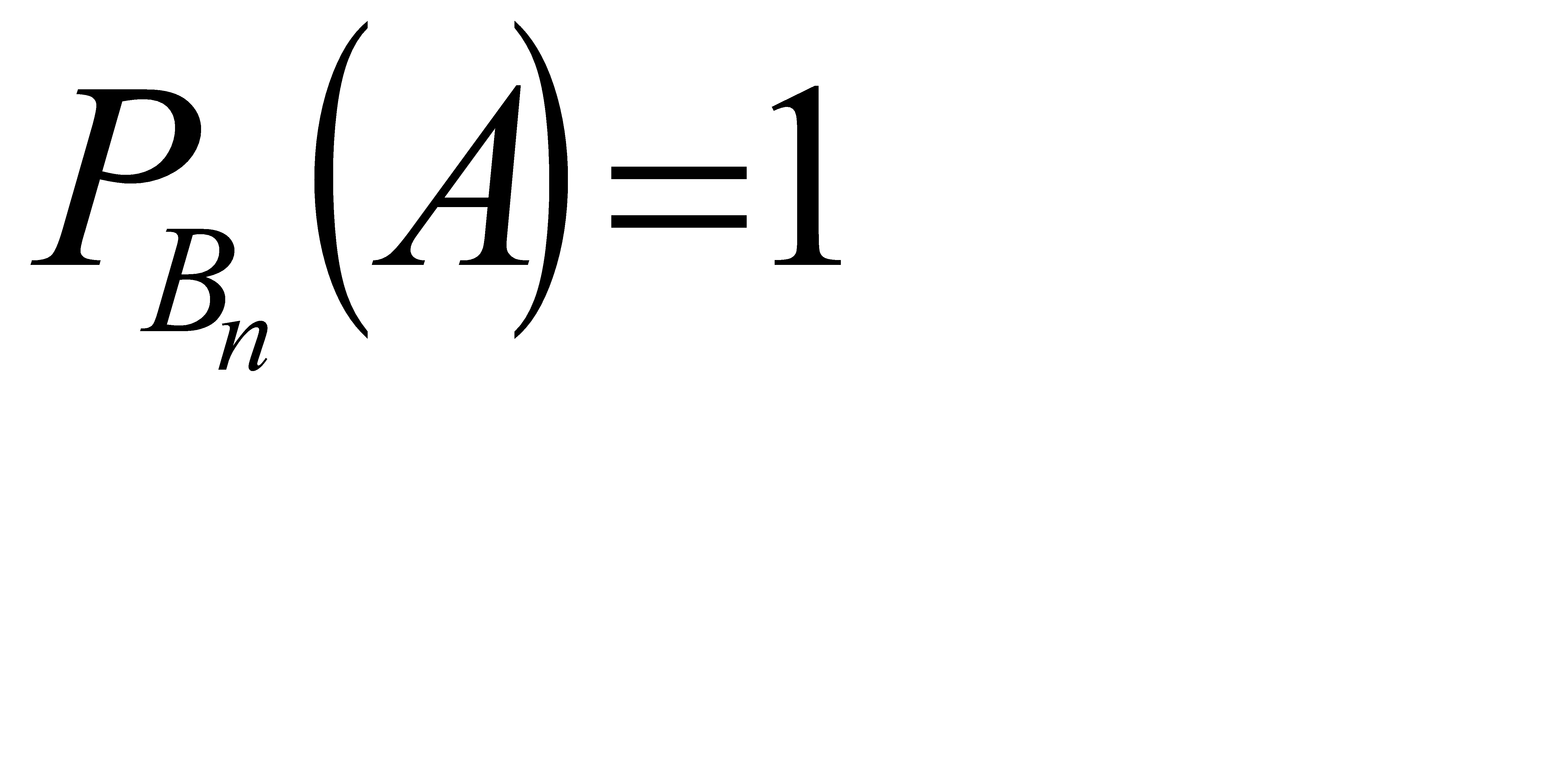 .
.
Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:

#91Решение: обозначим через  событие – произведен расчет на наудачу выбранной машине. Возможны следующие гипотезы в данном эксперименте:
событие – произведен расчет на наудачу выбранной машине. Возможны следующие гипотезы в данном эксперименте:  - расчет производится на клавишном автомате,
- расчет производится на клавишном автомате, 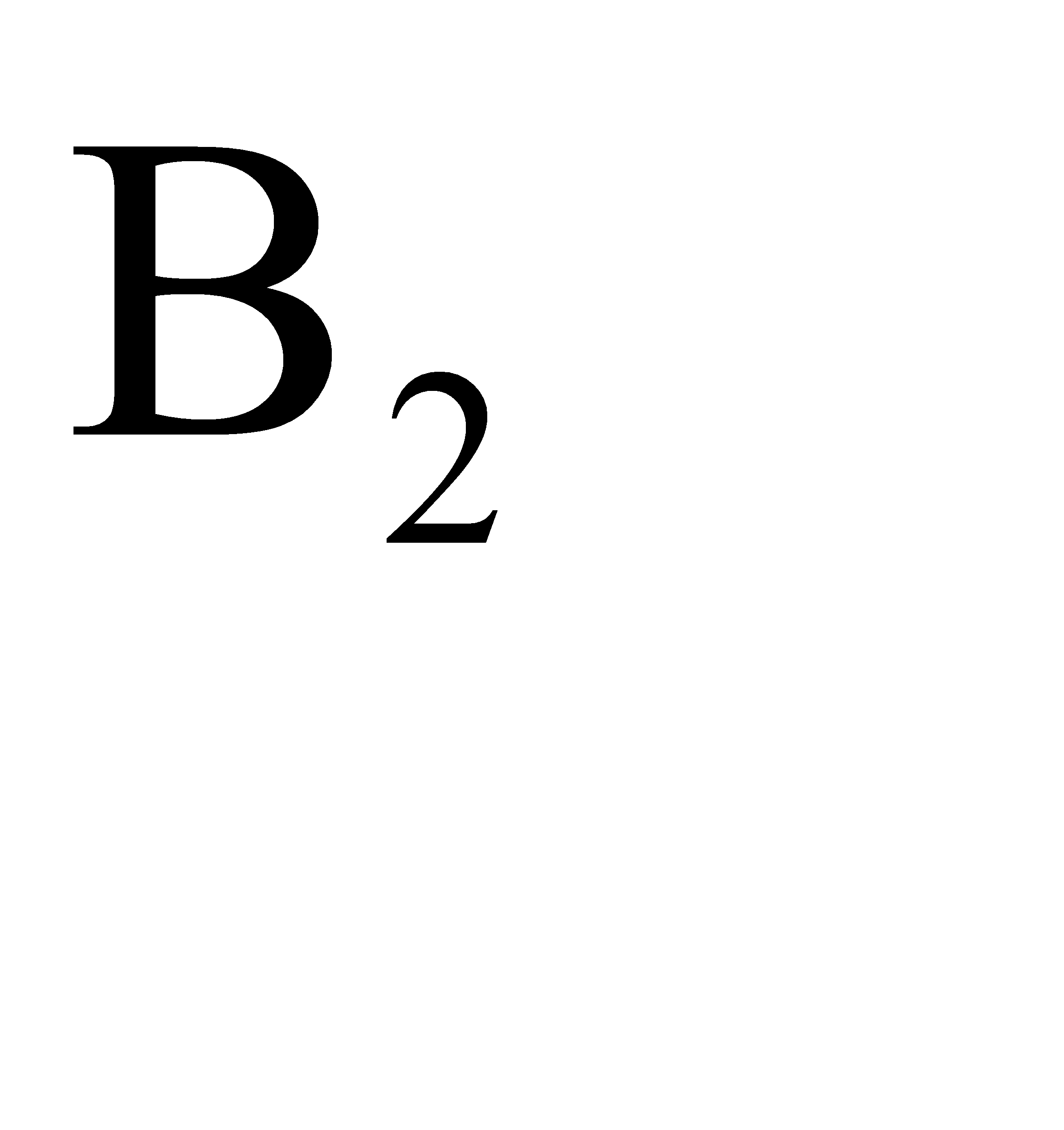 - расчет производится на полуавтомате. Так как имеется 6 клавишных автоматов и 4 полуавтомата, то вероятность того, что произойдет гипотеза
- расчет производится на полуавтомате. Так как имеется 6 клавишных автоматов и 4 полуавтомата, то вероятность того, что произойдет гипотеза  , равна
, равна 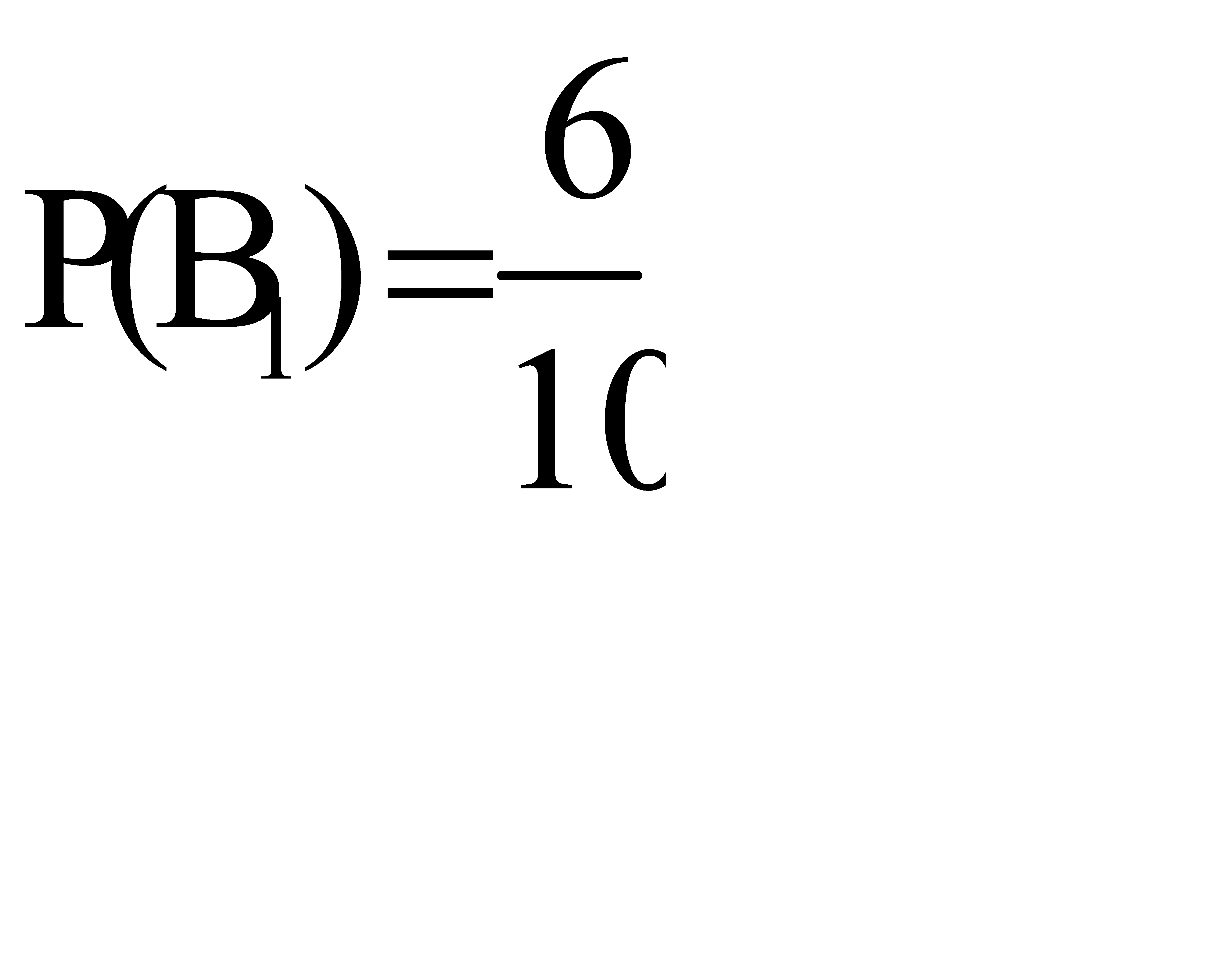 . А вероятность того, что произойдет гипотеза
. А вероятность того, что произойдет гипотеза 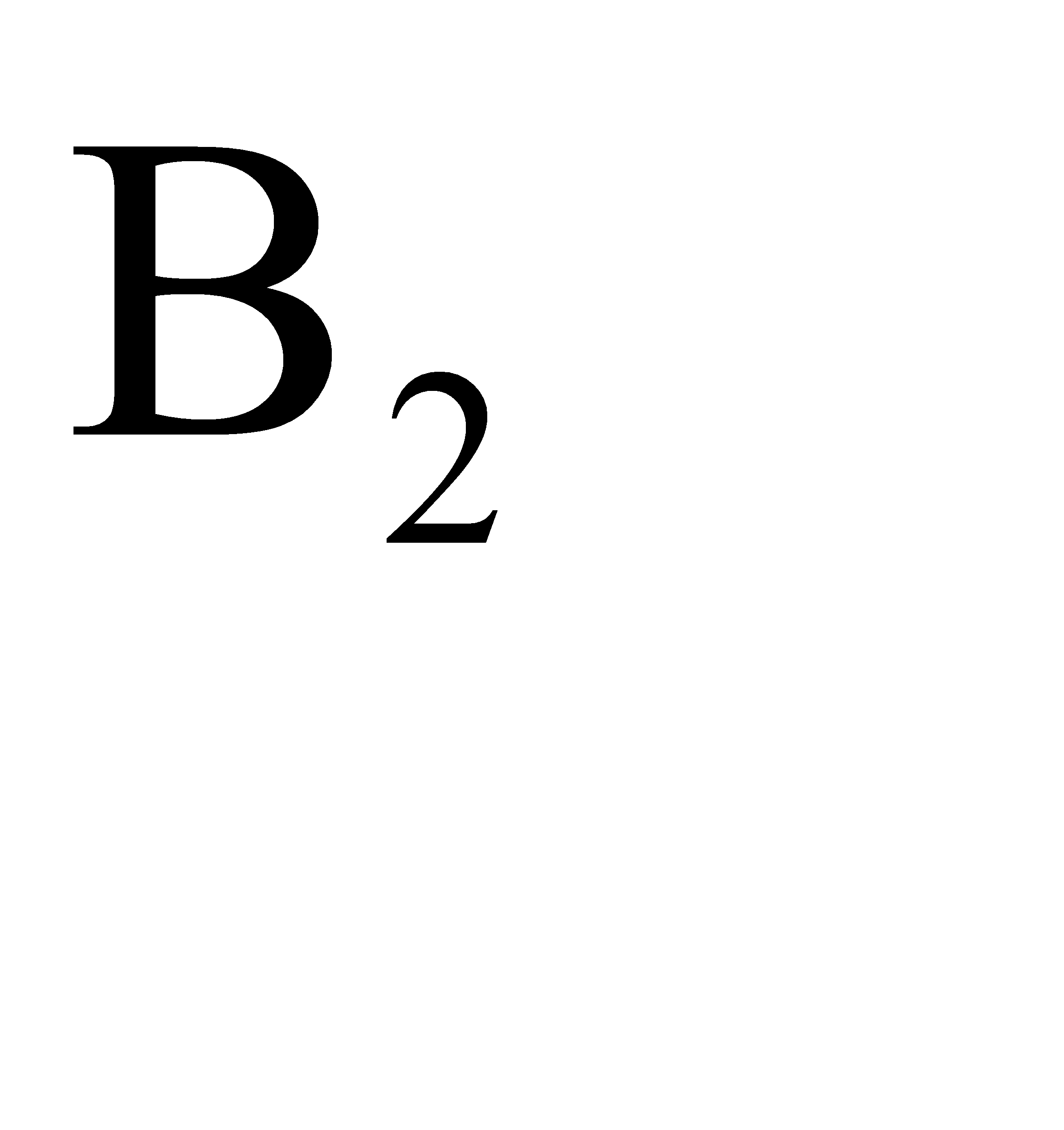 , равна
, равна 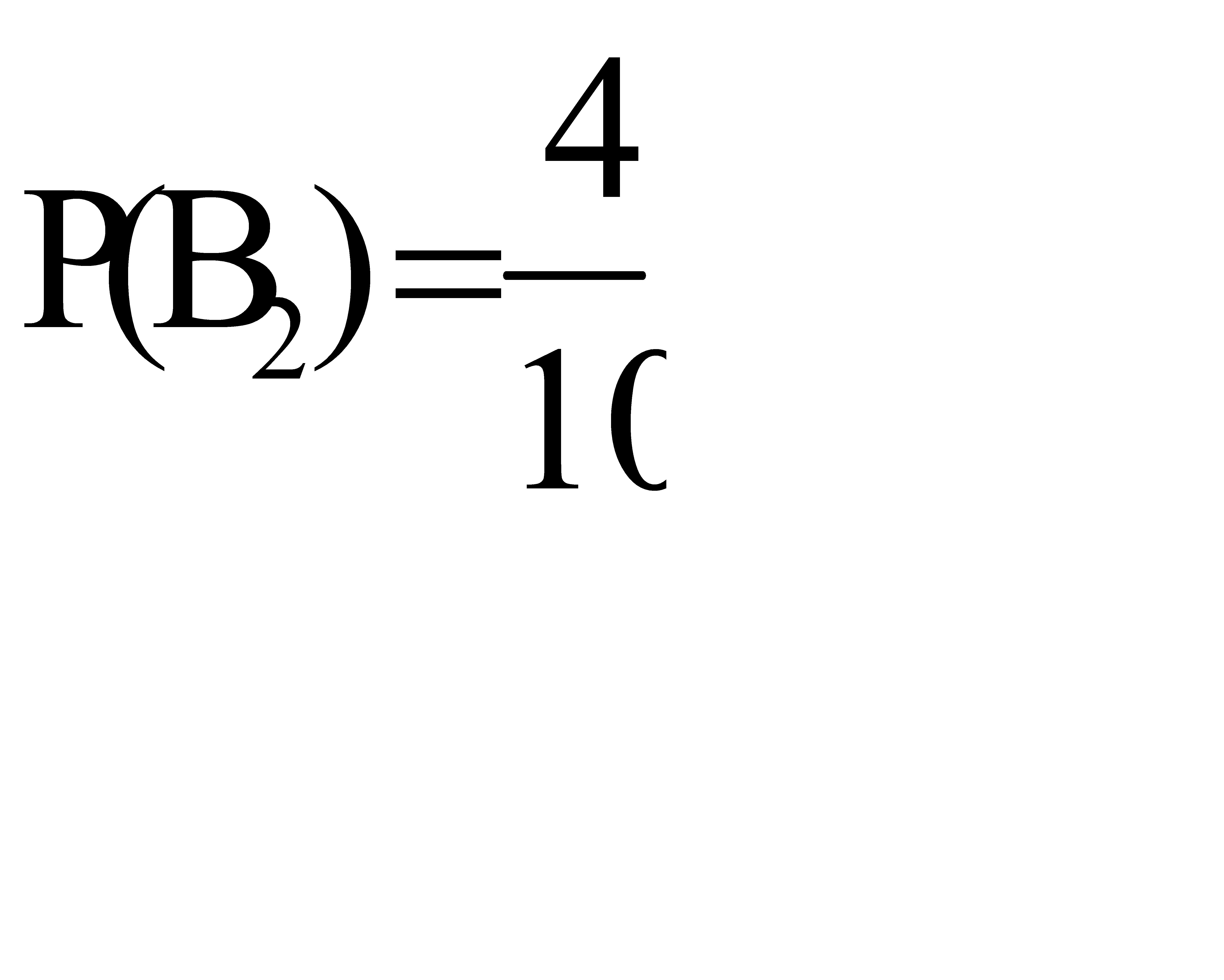 .
.
Условная вероятность того, что клавишный автомат не выйдет из строя, равна 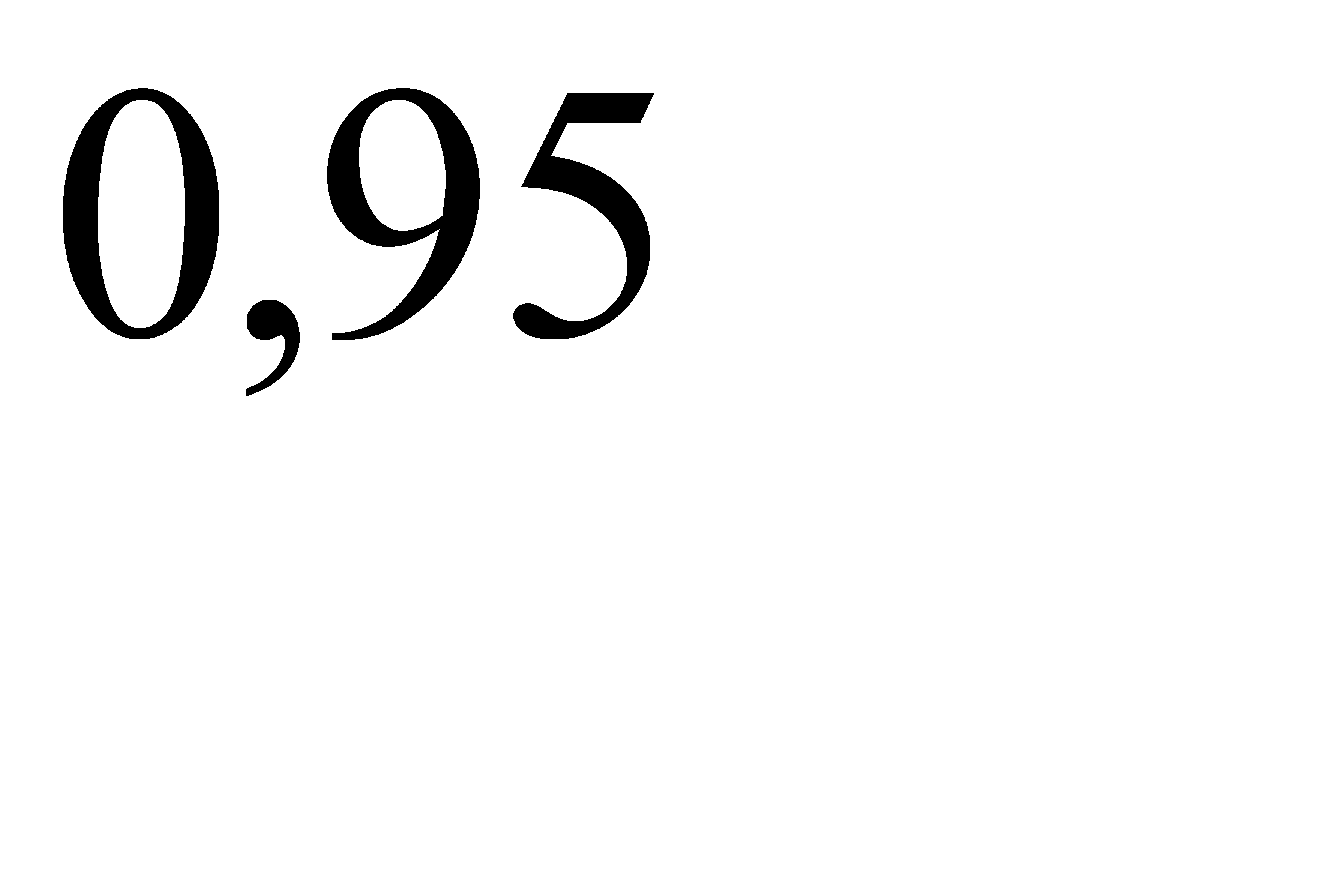 , т. е
, т. е 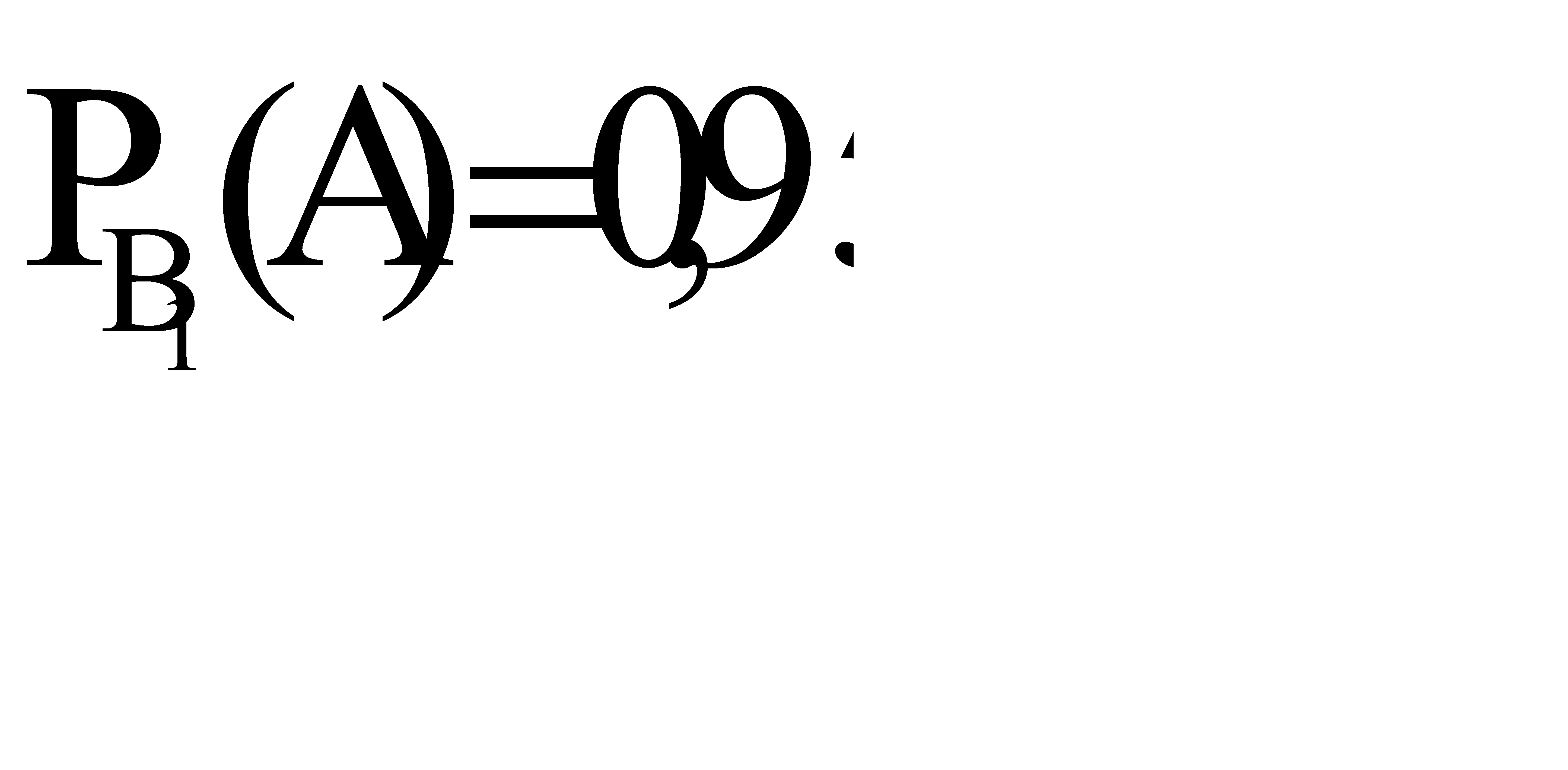 . А условная вероятность того, что полуавтомат не выйдет из строя, равна
. А условная вероятность того, что полуавтомат не выйдет из строя, равна 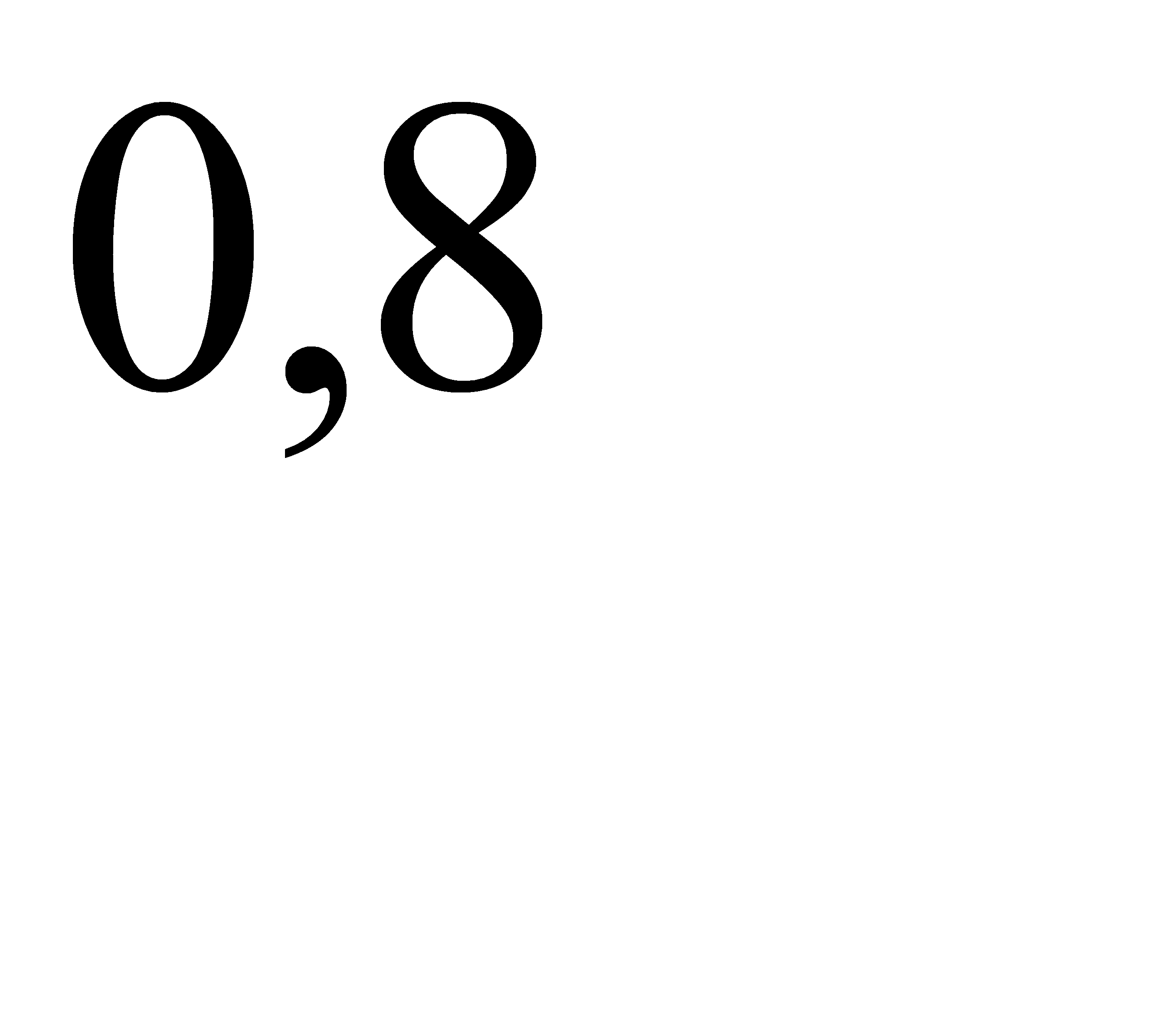 , т. е
, т. е 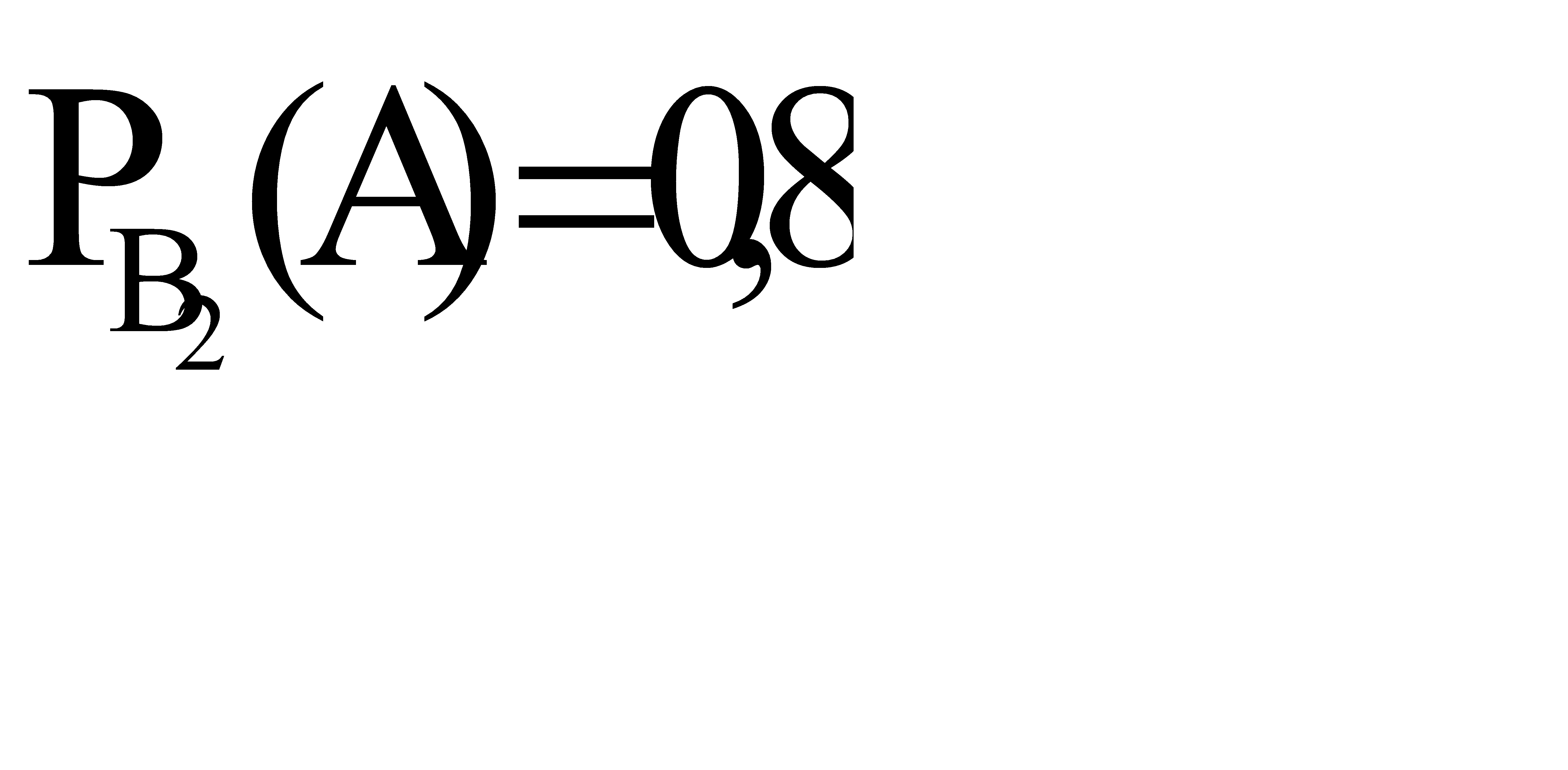 . Искомая вероятность того, что до окончания эксперимента машина не выйдет из строя, находим по формуле полной вероятности:
. Искомая вероятность того, что до окончания эксперимента машина не выйдет из строя, находим по формуле полной вероятности:
 Ответ: P(A)=0, 89
Ответ: P(A)=0, 89
#92Рассмотрим события: A – стрелок поразит мишень, В1 – взятая наудачу винтовка снабжена оптическим прицелом
В2 – взятая наудачу винтовка без оптического прицела. Следовательно, по условию, вероятность события А при условии события В1: 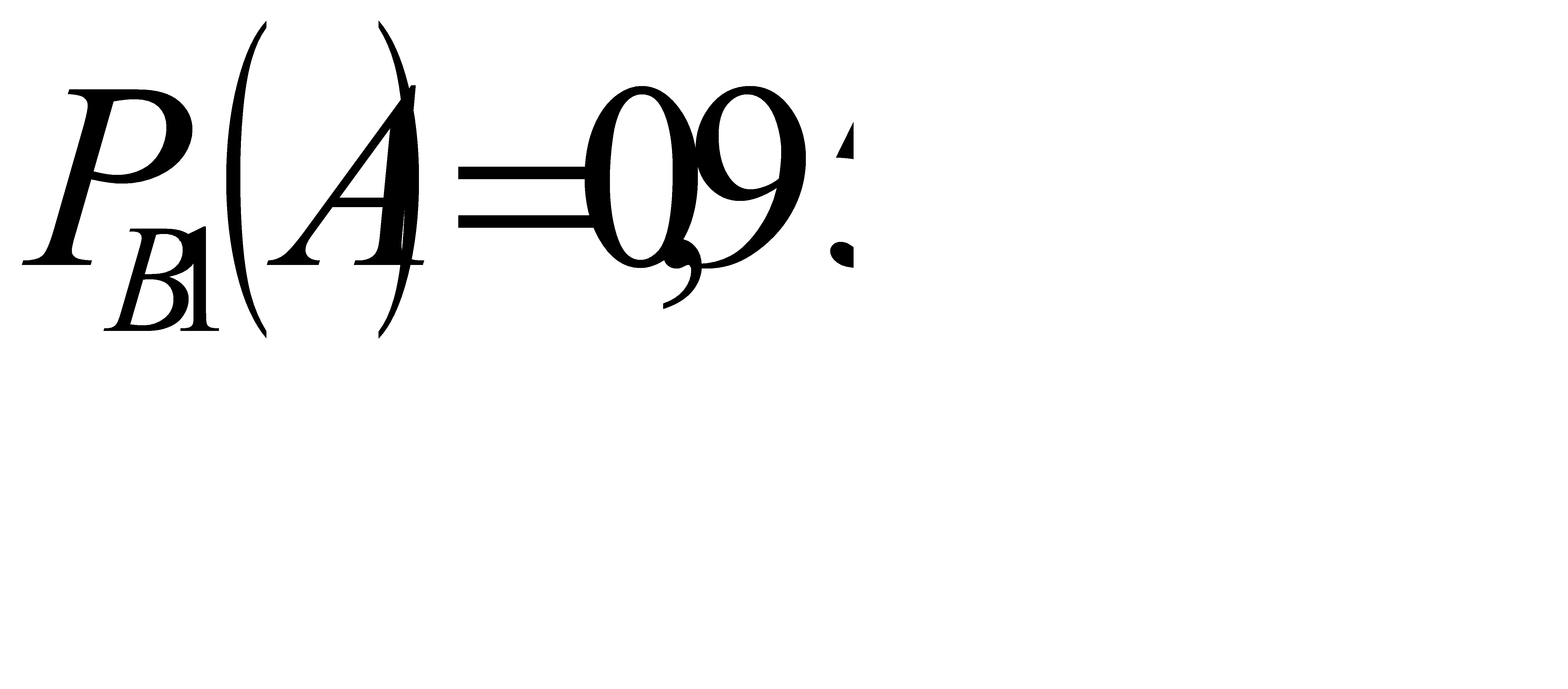 , а вероятность события А при условии события В2:
, а вероятность события А при условии события В2: 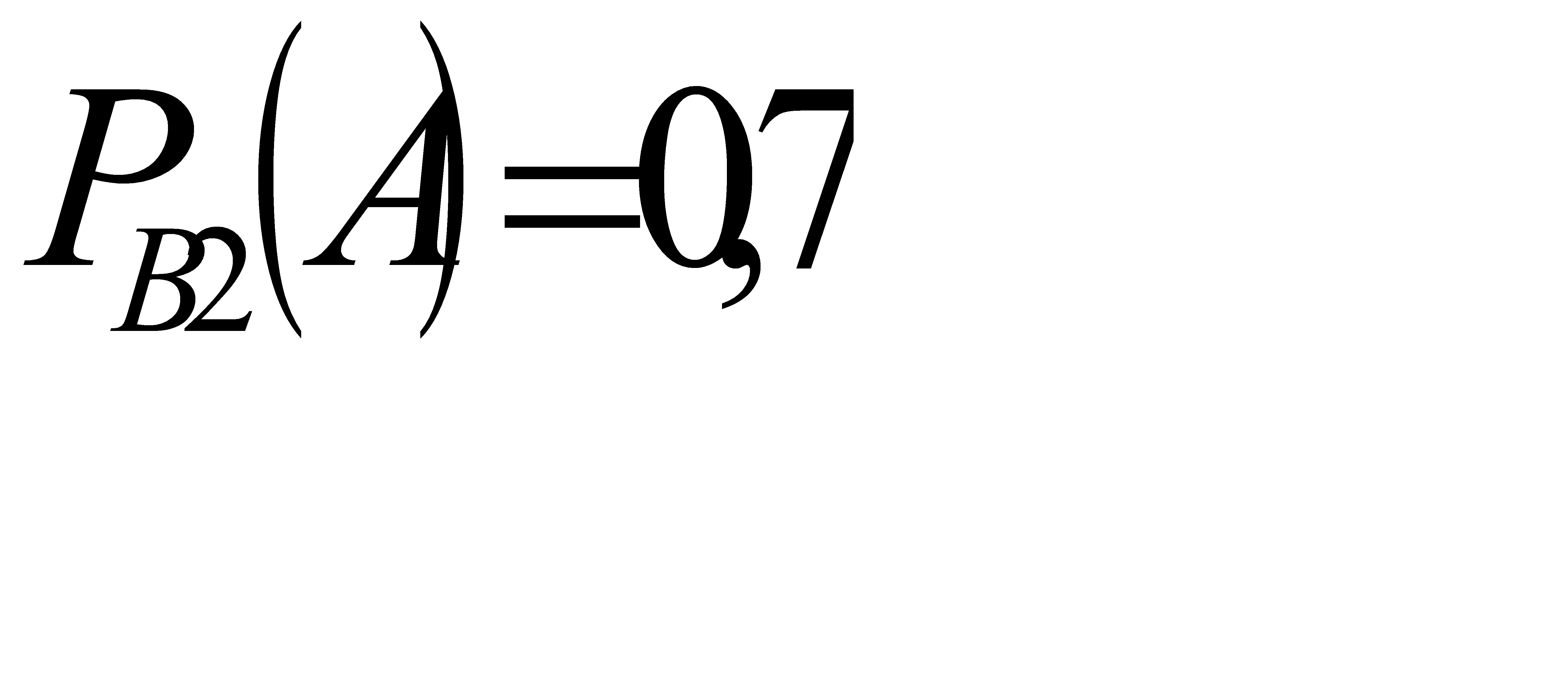 .
.
В свою очередь вероятность события В1: 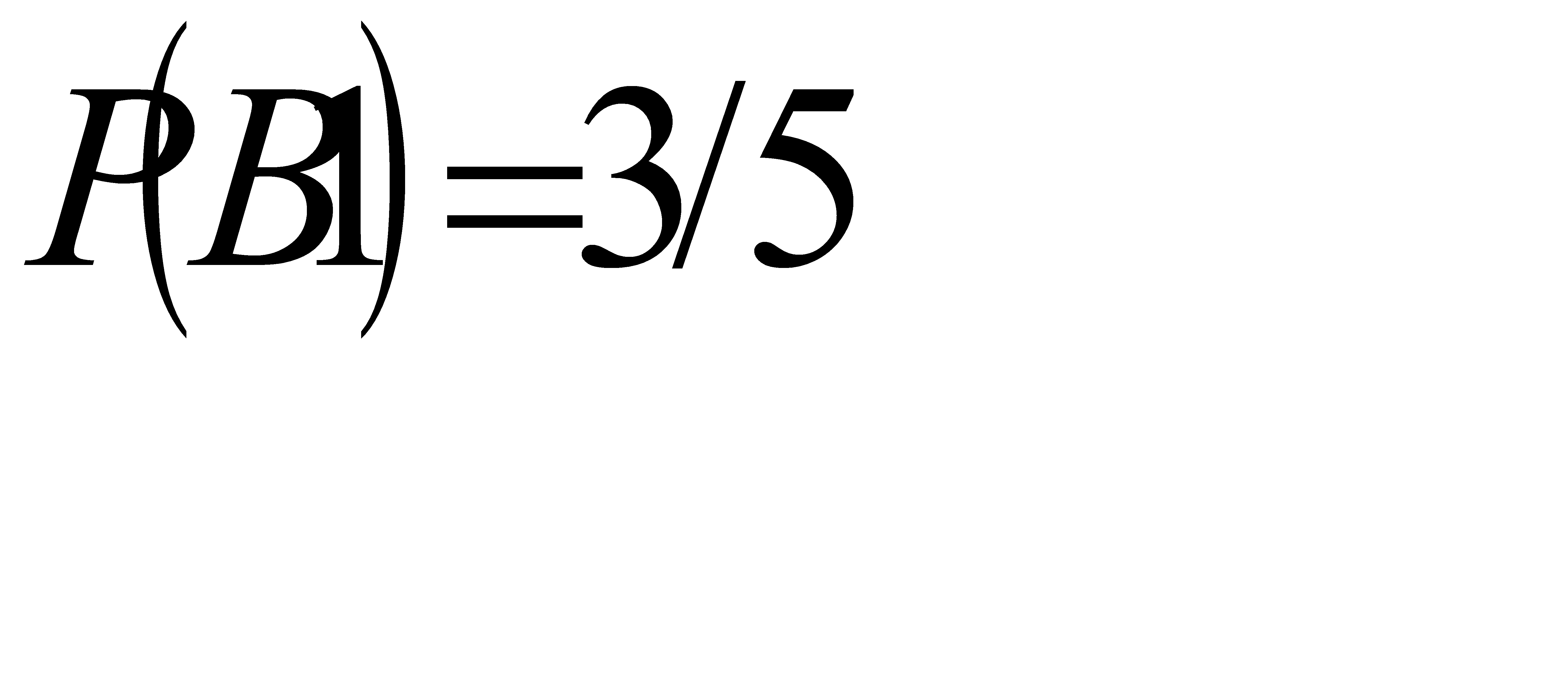 , т. к. всего винтовок 5, а благоприятствуют событию 3 винтовки. Аналогично
, т. к. всего винтовок 5, а благоприятствуют событию 3 винтовки. Аналогично 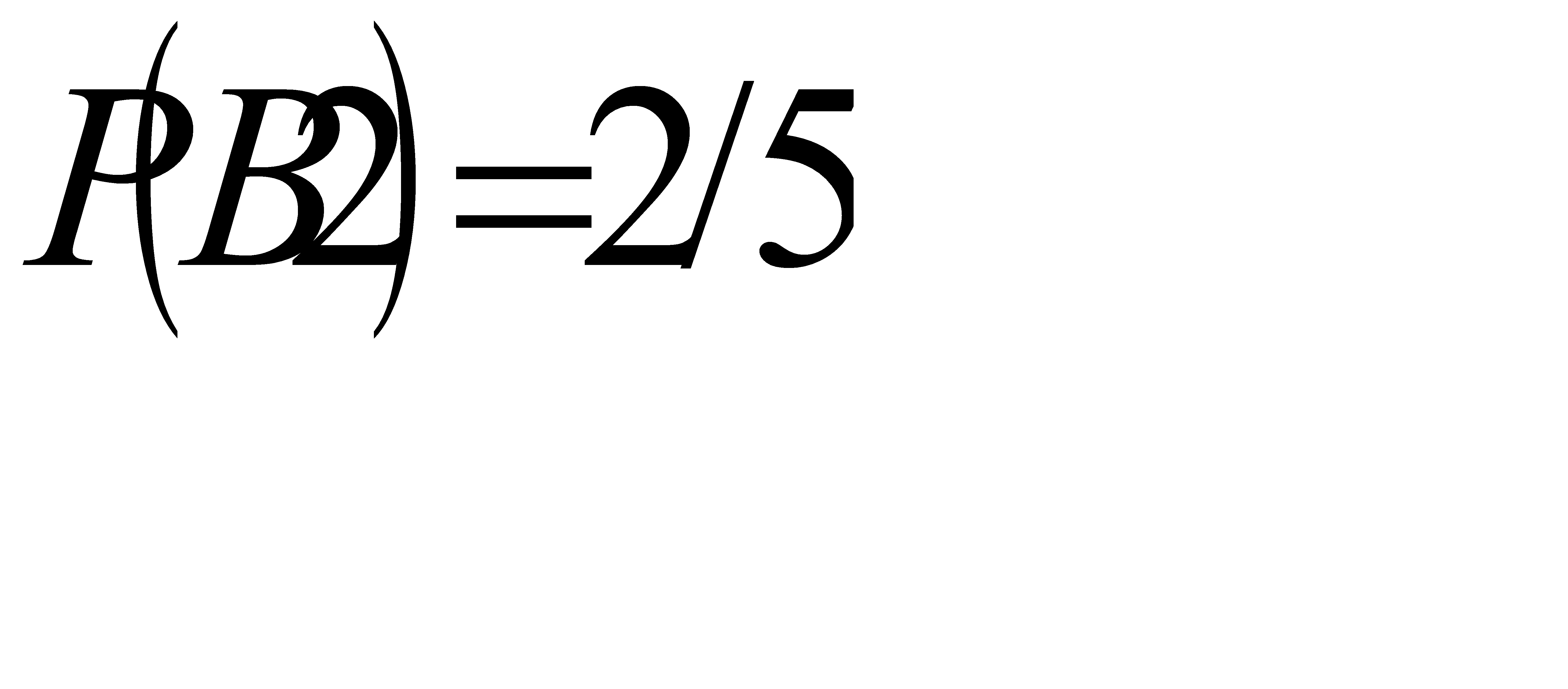 . Пользуясь формулой полной вероятности
. Пользуясь формулой полной вероятности 
 , получим:
, получим:
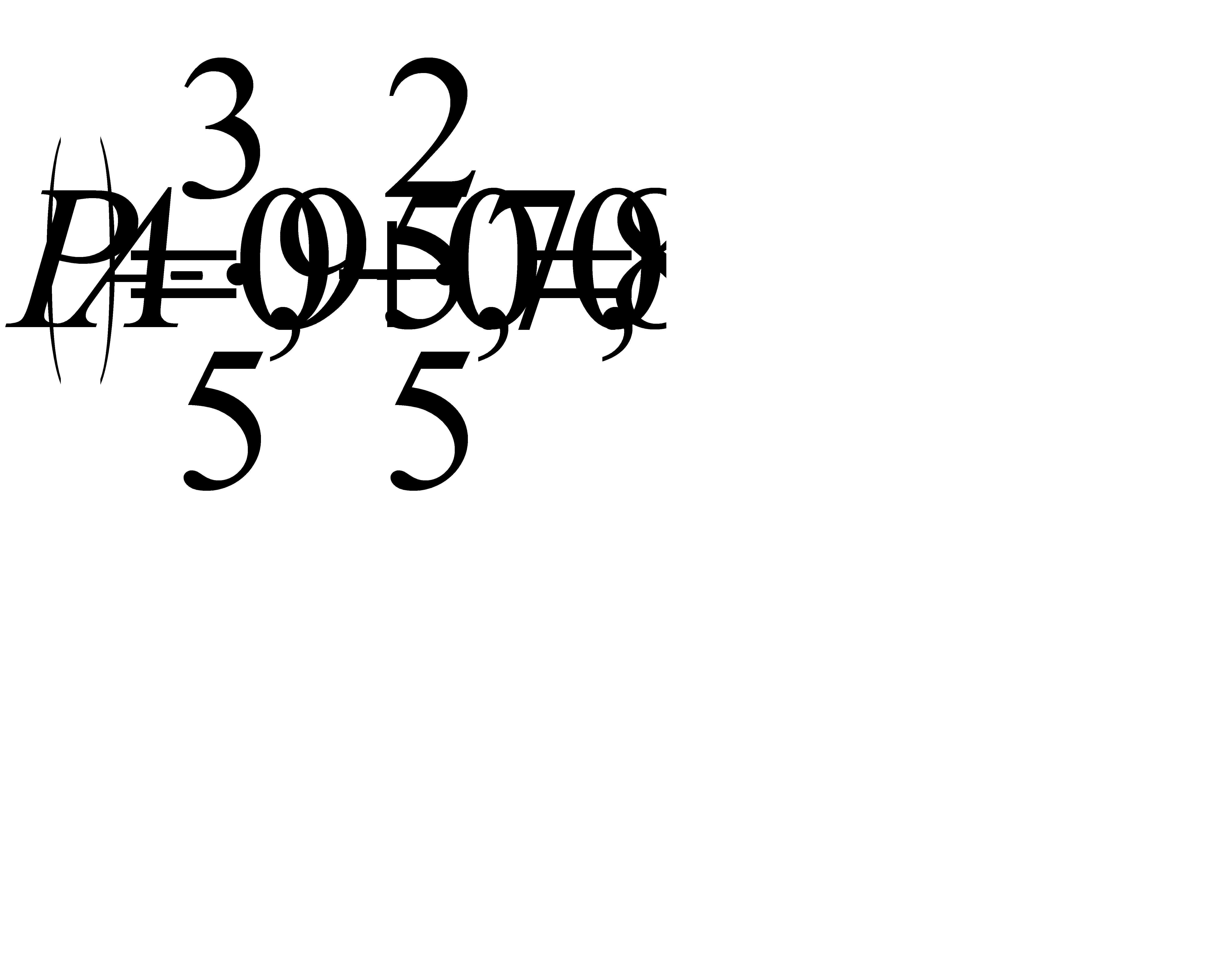 Ответ: 0, 85
Ответ: 0, 85
#93Решение: Обозначим через A событие – извлечена деталь отличного качества. Возможно три варианта гипотезы: 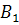 – извлечена деталь отличного качества, изготовленная заводе №1;
– извлечена деталь отличного качества, изготовленная заводе №1; 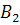 – извлечена деталь отличного качества, изготовленная заводе №2;
– извлечена деталь отличного качества, изготовленная заводе №2; 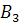 – извлечена деталь отличного качества, изготовленная заводе №3. По условию
– извлечена деталь отличного качества, изготовленная заводе №3. По условию 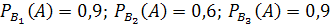 . Найдём вероятности того, что извлечённая деталь изготовлена на заводе №1, №2, №3.
. Найдём вероятности того, что извлечённая деталь изготовлена на заводе №1, №2, №3. 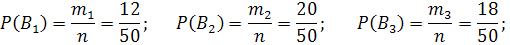
где 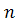 - общее число изготовленных на 3-х заводах деталей,
- общее число изготовленных на 3-х заводах деталей, 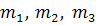 – количество деталей изготовленных, соответственно, на заводах №1, 2, 3.
– количество деталей изготовленных, соответственно, на заводах №1, 2, 3.
Искомая вероятность вероятность того, что извлеченная наудачу деталь окажется отличного качества находится по формуле полной вероятности:
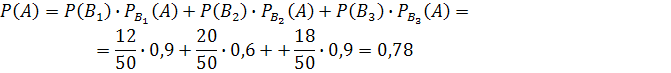
#94Обозначим через  событие – извлечён белый шар. Возможны следующие гипотезы:
событие – извлечён белый шар. Возможны следующие гипотезы: 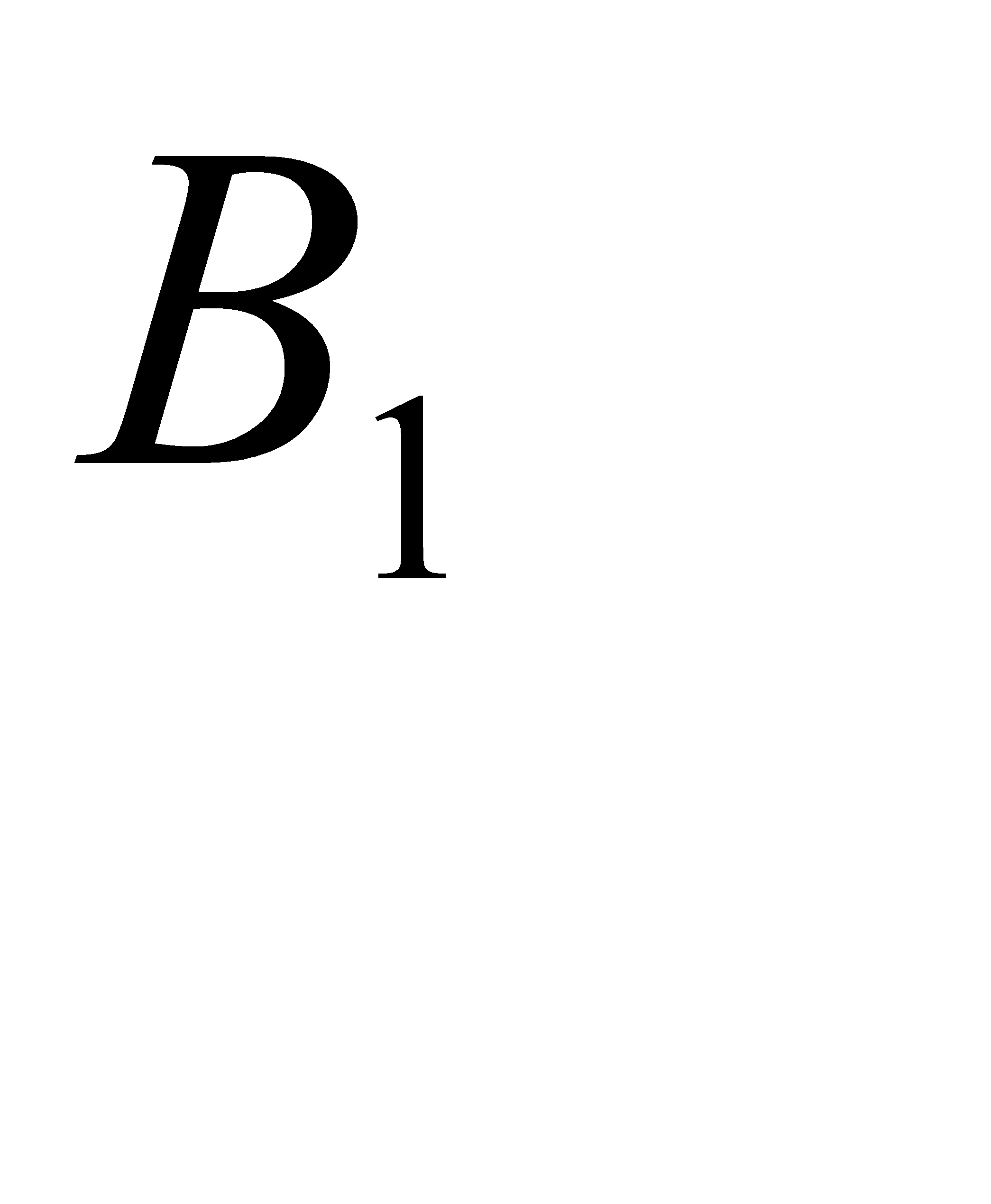 - белый шар взят из первой урны,
- белый шар взят из первой урны, 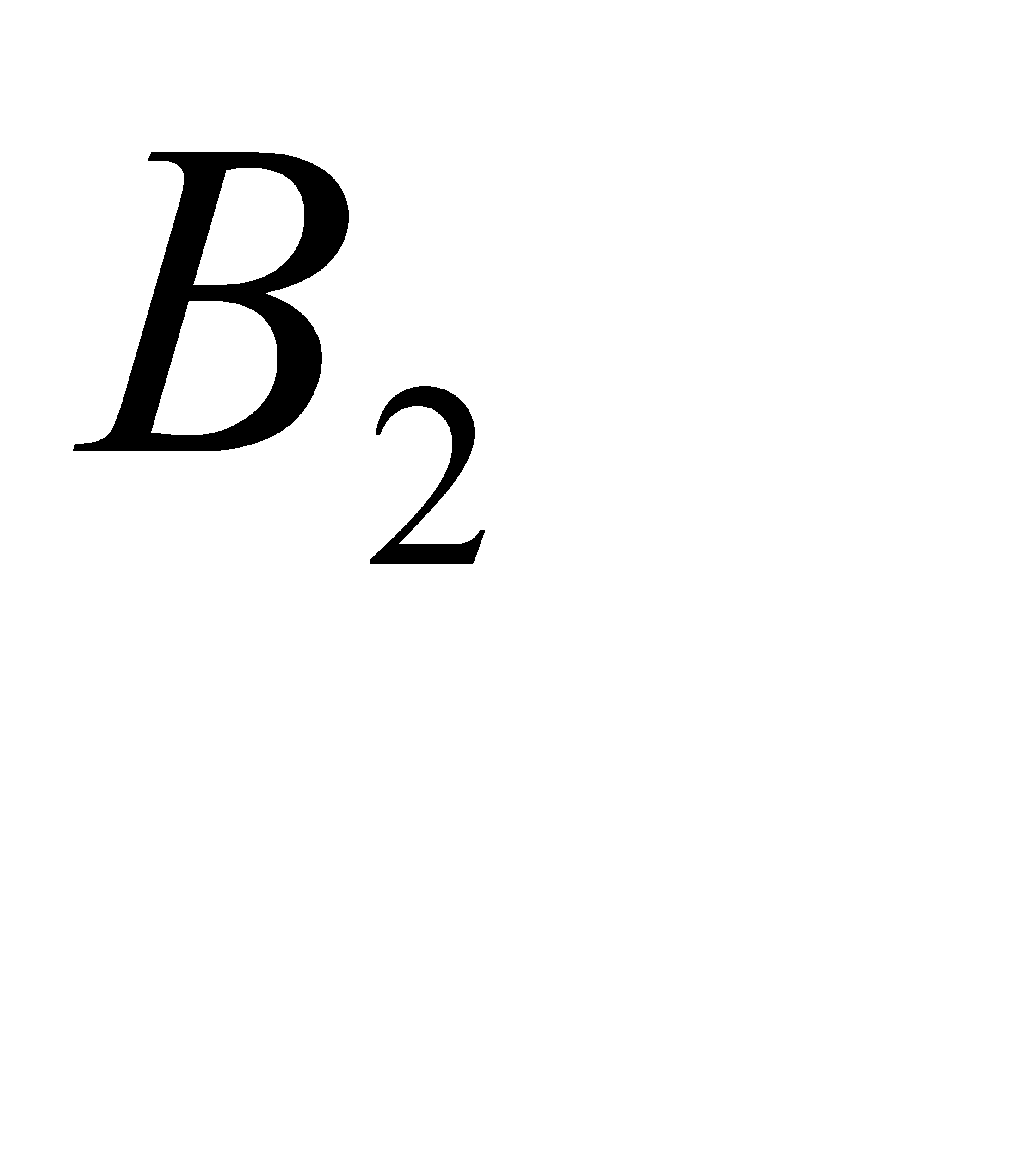 - белый шар взят из второй урны. Поскольку всего имеется две гипотезы, причём по условию они равновероятны, и сумма вероятностей гипотез равна единице(т. к. они образуют полную группу событий), то вероятность каждой из гипотез равна
- белый шар взят из второй урны. Поскольку всего имеется две гипотезы, причём по условию они равновероятны, и сумма вероятностей гипотез равна единице(т. к. они образуют полную группу событий), то вероятность каждой из гипотез равна  , т. е.
, т. е. 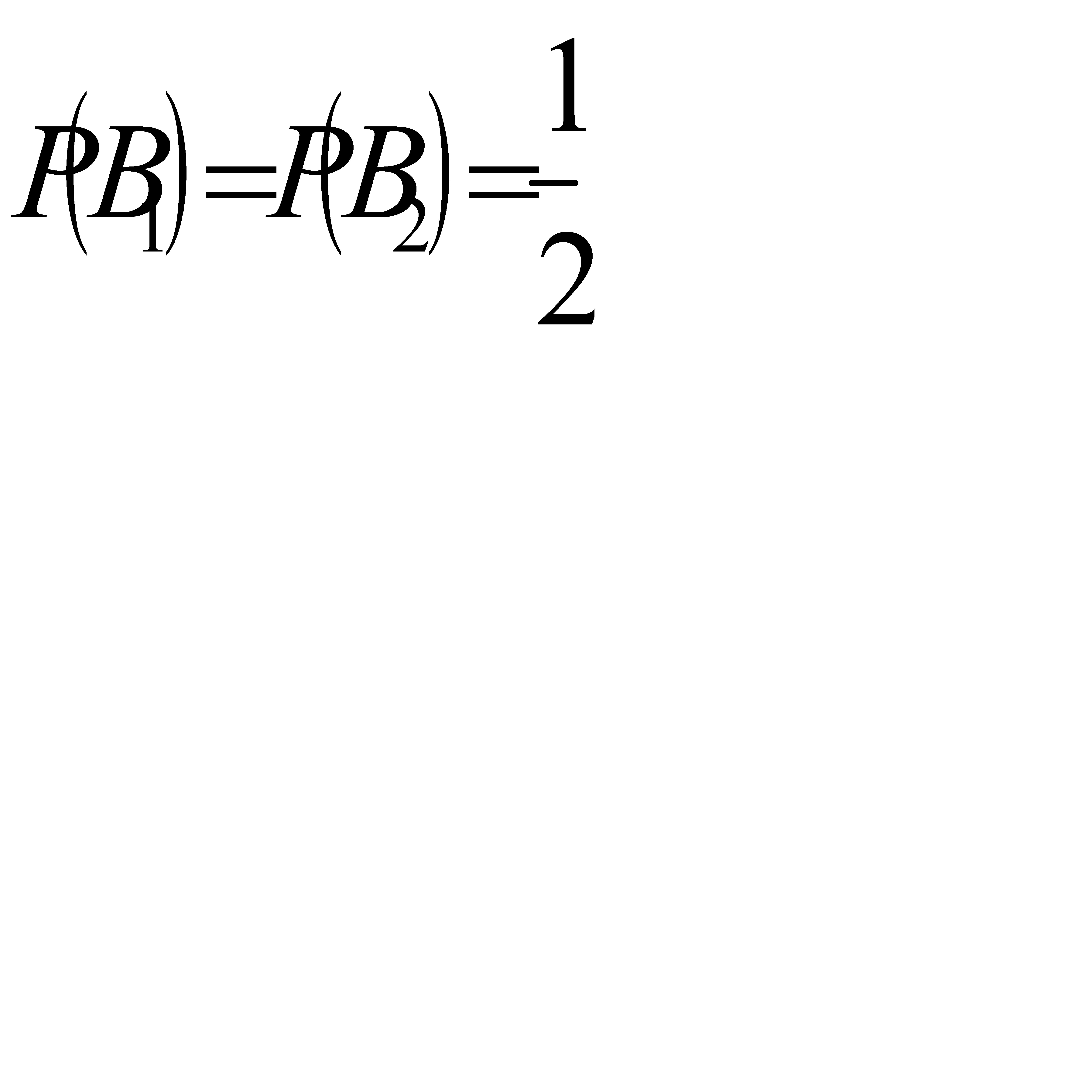 . Условная вероятность того, что белый шар будет извлечён из первой урны равна:
. Условная вероятность того, что белый шар будет извлечён из первой урны равна: 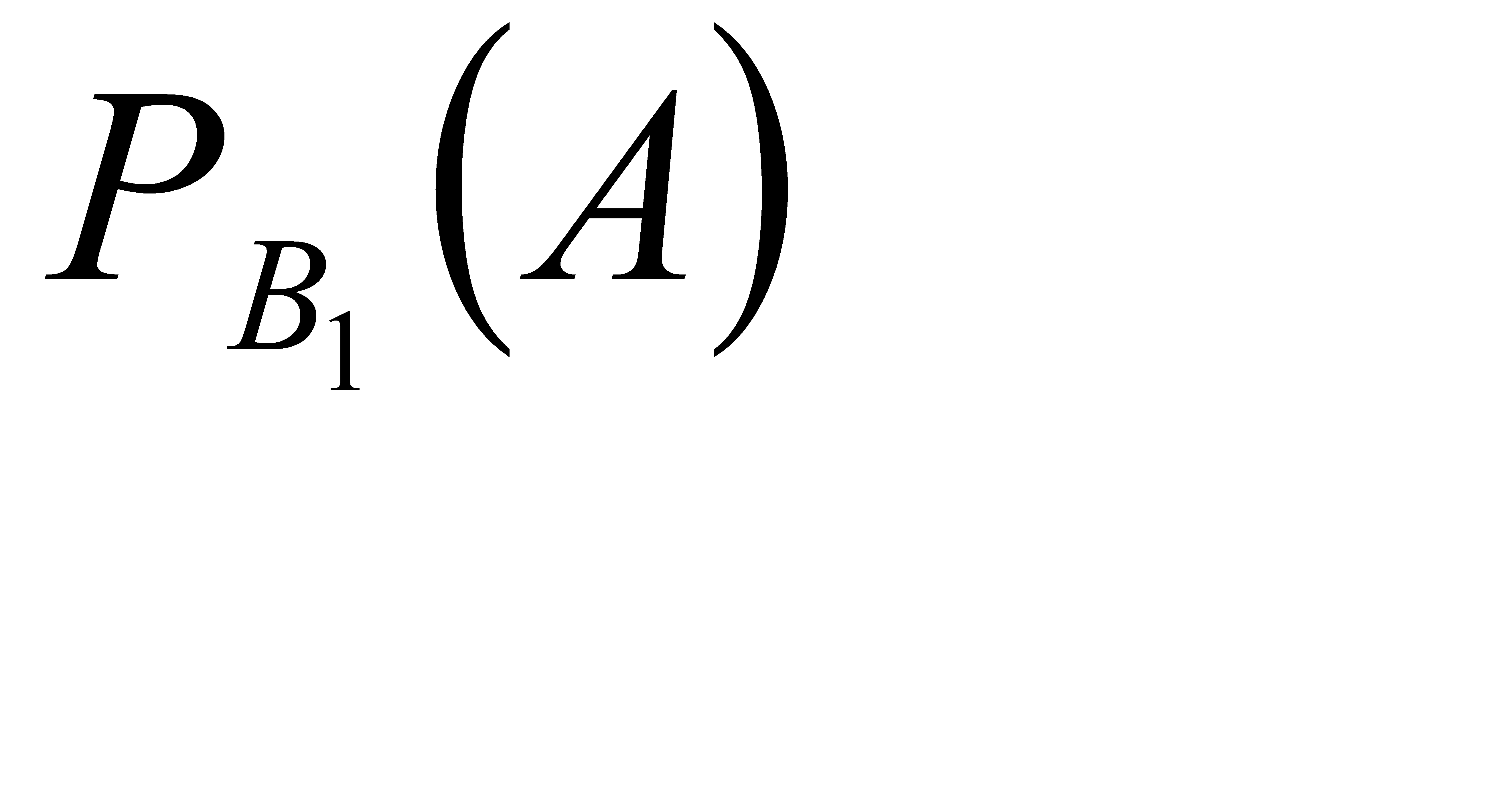 =
= 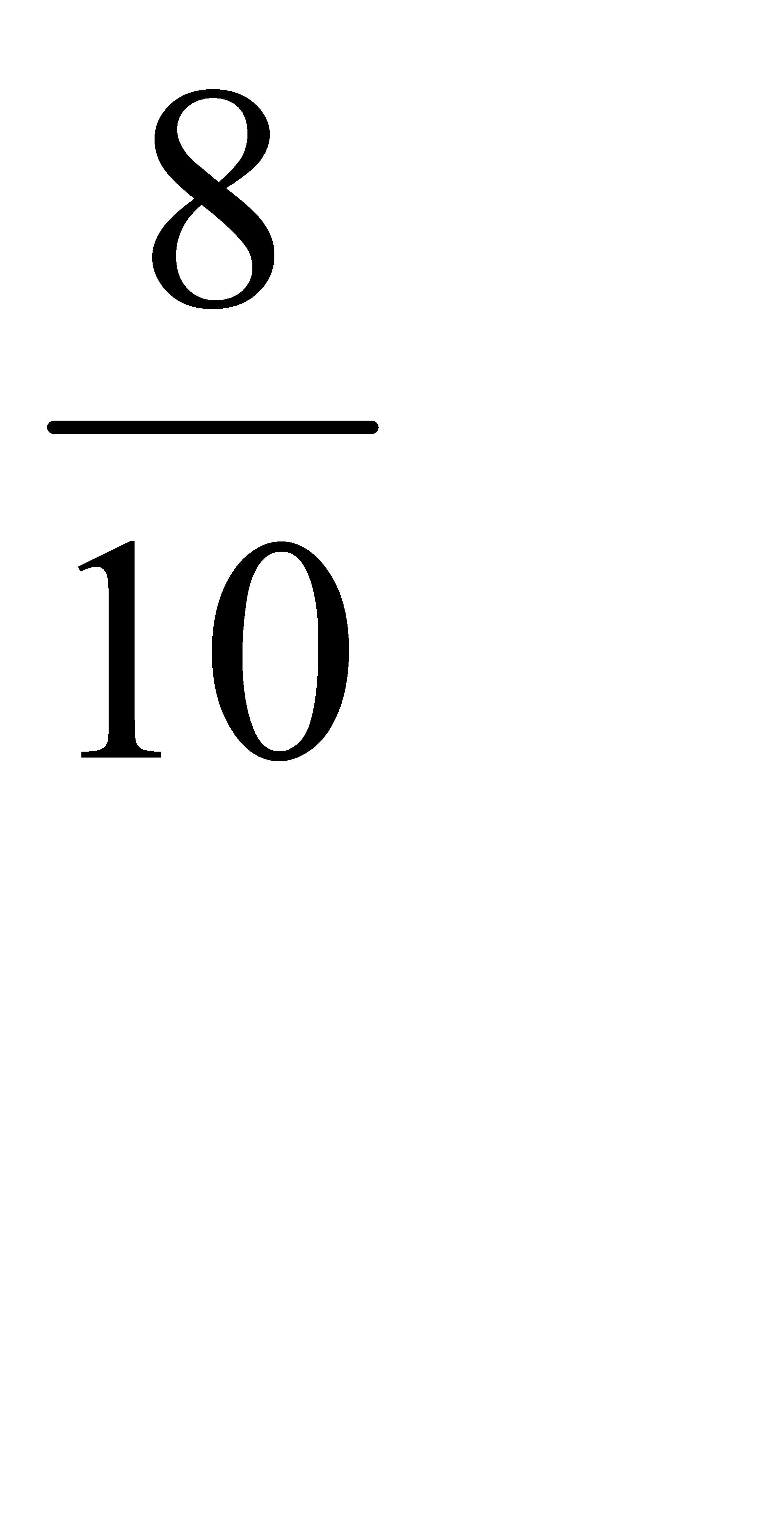 Условная вероятность того, что белый шар будет извлечён из второй урны равна:
Условная вероятность того, что белый шар будет извлечён из второй урны равна: 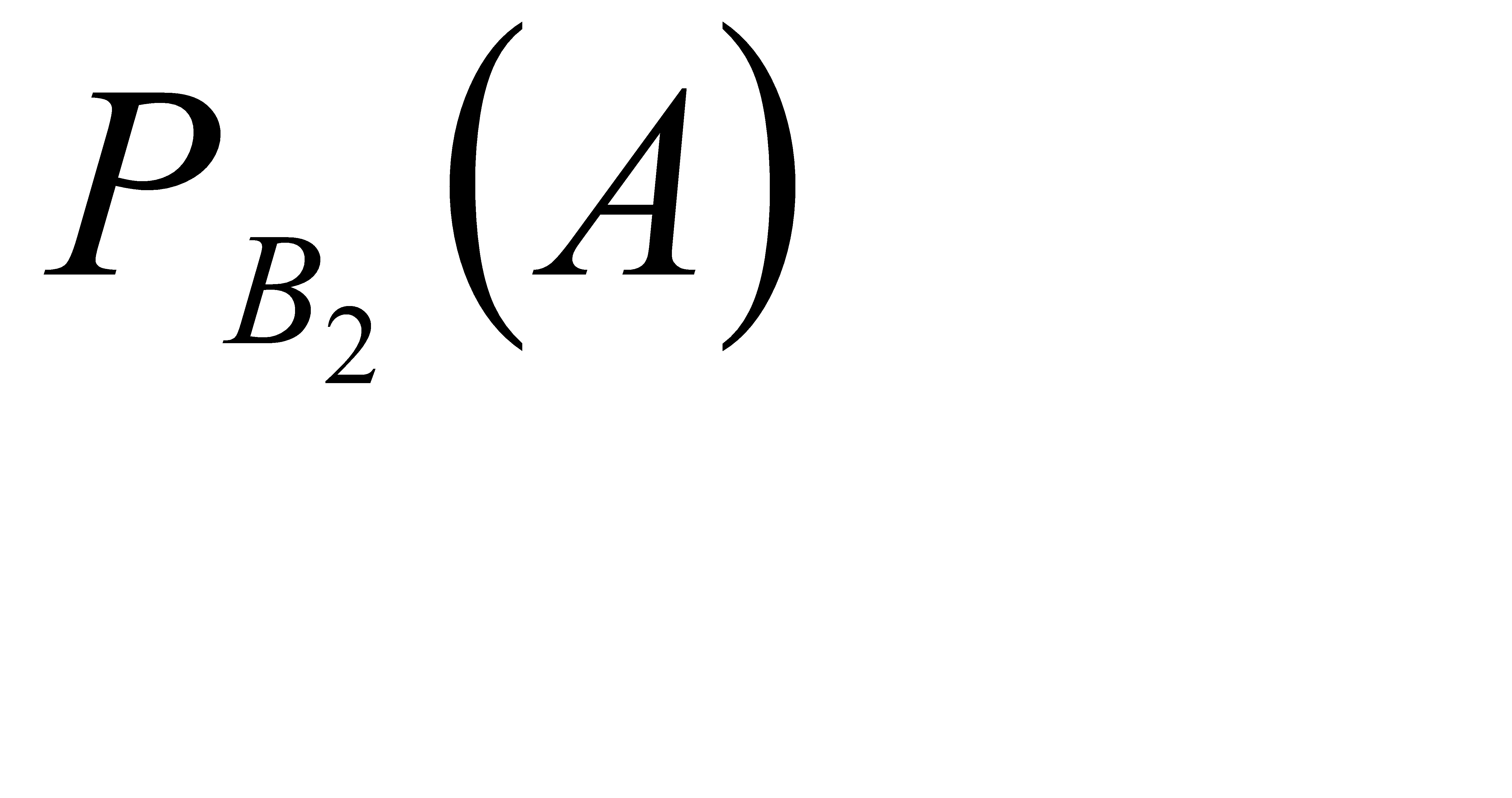 =
= 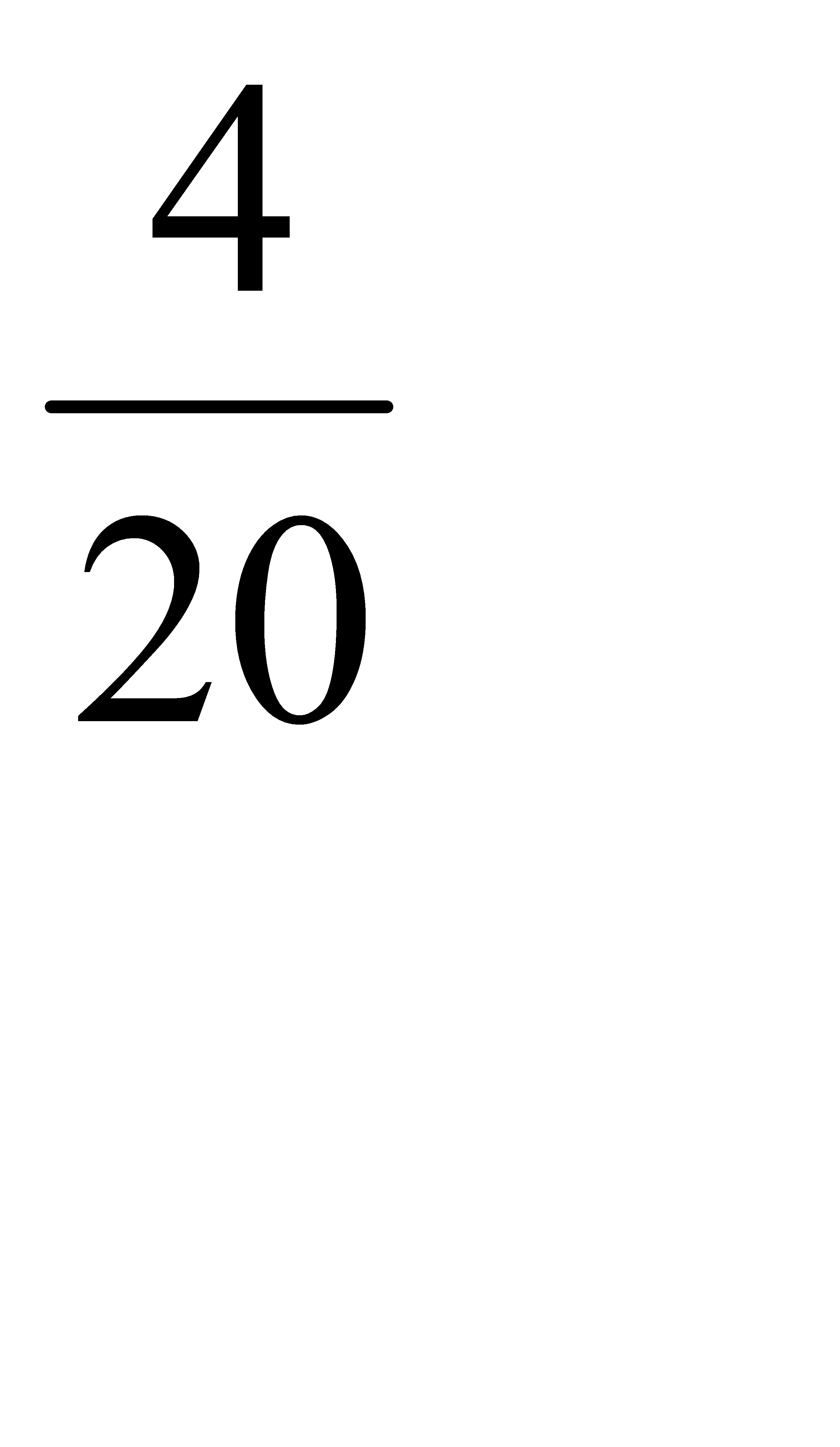
По формуле полной вероятности находим:

#95A1 – вероятность того, что из первой урны извлечен белый шар. A2 – вероятность того, что из первой урны извлечен черный шар. P(A1)=4/10 P(A2)=6/10B1 – вероятность того, что из второй урны извлечен белый шар, после того как из первой урны переложили во вторую урну белый шар. B2 – вероятность того, что из второй урны извлечен белый шар, после того как из первой урны переложили во вторую урну черный шар. P(B1)=5/11 P(B2)=4/11
C1 – вероятность того, что из второй корзины будет извлечен белый шар.
C2 – вероятность того, что из второй корзины будет извлечен черный шар.
P(C1)=P(A1)*P(B1)+P(A2)*P(B2) P(C1)=4/10*5/11+6/10*4/11=2/5
P(C2)=1-P(C1) P(C2)=1-2/5=3/5
D1 – вероятность того, что из третьей урны извлечен белый шар, после того как из второй урны переложили в втретью урну белый шар. D2 – вероятность того, что из третьей урны извлечен белый шар, после того как из второй урны переложили в втретью урну черный шар. P(D1)=5/11 P(D2)=4/11
E – вероятность того, что из третьей урны будет извлечен белый шар.
P(E)= P(D1)*P(C1)+P(D2)*P(C2) P(E)=5/11*2/5+4/11*3/5=2/5
Ответ: 2/5.
#96Решение: Пусть А – событие того, что сбой будет обнаружен, тогда из формулы полной вероятности следует, что:
PA= PB1PB1A+PB2PB2A+PB3PB3A= 0, 3*0, 8+0, 2*0, 9+0, 5*0, 9=0, 87.
#97
Обозначим через А событие – деталь отличного качества
Можно сделать два предположения 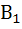 -деталь произведена первым автоматом (так как производительность первого автомата вдвое больше второго автомата, то Р(
-деталь произведена первым автоматом (так как производительность первого автомата вдвое больше второго автомата, то Р( 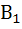 )=2/3)
)=2/3)
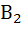 -деталь произведена вторым автоматом (Р(
-деталь произведена вторым автоматом (Р( 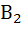 )=1/3)
)=1/3)
Условная вероятность, что она будет отличного качества, если она произведена первым автоматом 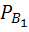 (A)=0, 6
(A)=0, 6
Условная вероятность, что она будет отличного качества, если она произведена первым автоматом 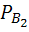 (A)=0, 84
(A)=0, 84
Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности равна
P(A)=Р( 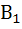 )*
)* 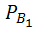 (A)+ Р(
(A)+ Р( 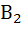 )*
)* 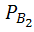 (A)=2/3*0. 6+1/3*0. 84=0. 68
(A)=2/3*0. 6+1/3*0. 84=0. 68
Вероятность того, что взятая отличная деталь произведена первым автоматом, по формуле Бейеса равна
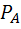 (
( 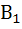 )=
)= 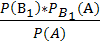 =
= 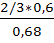 =
= 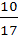
Ответ: 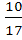
#98Решение: Обозначим событие А – стрелок поразил мишень и гипотезы: B1 – стрелок выбрал винтовку с оптическим прицелом, B2 – без оптического прицела. Тогда 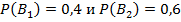 . Условные вероятности попадания из винтовки с оптическим прицелом и без:
. Условные вероятности попадания из винтовки с оптическим прицелом и без: 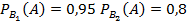 . Вычислим вероятность попадания из наудачу взятой винтовки:
. Вычислим вероятность попадания из наудачу взятой винтовки: 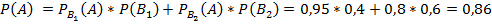
Теперь, воспользовавшись формулой Бейеса, получим ответ:
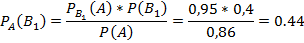
Ответ: Стрелок вероятнее всего стрелял из винтовки без оптического прицела.
#99 Обозначим через А событие—подъезд автомобиля к заправке. Можно сделать два предположения: 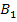 —проехал грузовой автомобиль, причем
—проехал грузовой автомобиль, причем 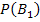 =3/5;
=3/5; 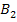 — проехал легковой автомобиль, причем
— проехал легковой автомобиль, причем 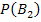 = 2/5.
= 2/5.
Условная вероятность, что проезжающий грузовой автомобиль подъедет на заправку: 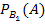 = 0, 1. Для легкового:
= 0, 1. Для легкового: 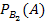 = 0, 2.
= 0, 2.
Вероятность того, что проезжающий автомобиль подъедет на заправку, по формуле полной вероятности равна Р(А) = 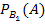
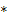
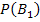 +
+ 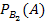
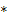
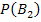 = 3/5
= 3/5 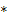 0, 1 + 2/5
0, 1 + 2/5 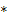 0, 2 = 0, 14
0, 2 = 0, 14
Искомая вероятность того, что подъехавший к заправке автомобиль будет грузовым, по формуле Бейеса равна 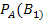 =
= 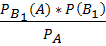 =
= 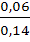 = 3/7Ответ: 3/7.
= 3/7Ответ: 3/7.
#100Обозначим через событие А – ошибку перфораторщицы. Тогда, 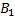 – ошибка сделана первой перфораторщицей,
– ошибка сделана первой перфораторщицей, 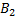 - ошибка сделана второй перфораторщицей. Причем P(
- ошибка сделана второй перфораторщицей. Причем P( 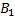 )=0, 5 и P(
)=0, 5 и P( 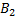 )=0, 5, т. к. обе работали одинаково.
)=0, 5, т. к. обе работали одинаково.
Условная вероятность того, что первая перфораторщица допустит ошибку, равна 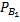 (A)=0, 05;
(A)=0, 05;
Условная вероятность того, что вторая перфораторщица допустит ошибку, равна 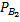 (A)=0, 1.
(A)=0, 1.
Вероятность того, что наудачу взятая перфокарта, окажется с ошибкой равна, по формуле полной вероятности равна:
P(A)= P( 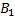 )*
)* 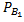 (A)+ P(
(A)+ P( 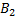 )*
)* 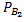 (A)=0, 5*0, 05+0, 5*0, 1=
(A)=0, 5*0, 05+0, 5*0, 1=  . Искомая вероятность того, что взятая перфокарта произведена первой перфораторщицей, по формуле Бейеса равна:
. Искомая вероятность того, что взятая перфокарта произведена первой перфораторщицей, по формуле Бейеса равна: 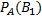 =
= 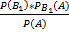 =
= 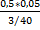 =
=  .
.
#101 Больные поступают в больницу в разном процентном соотношении. Р(k)= 0. 7, P(L)=0. 3, P(M)= 0. 2, где K, L, M – заболевания, а Р(Х)- вероятность поступления с данным заболеванием. Тогда Pk(A)=0. 7, Pl(A)=0. 8, Pm(A)=0. 9 это вероятность полного излечения от данного заболевания. Чтобы найти вероятность что Больной, поступивший в больницу, был выписан здоровым надо найти: P(A)= Pk(a)*P(k) + Pl(a)*P(l) + Pm(a)*P(m) = 0. 7*0. 5 + 0. 8*0. 3 + 0. 9*0. 2 = 0. 77
А вероятность что больной страдал именно заболеванием К равно: Pa(K) = (Pk(a)*P(k))/P(A)= (0. 5*0. 7)/0. 77 = 5/11
#102 Обозначим через А – изделие признана стандартной. 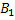 - вероятность того, что изделие попало к первому товароведу.
- вероятность того, что изделие попало к первому товароведу. 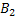 - ко второму. P(
- ко второму. P( 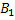 ) = 0, 55, P(
) = 0, 55, P( 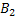 ) = 0, 45.
) = 0, 45.
Условная вероятность того что изделие будет признано стандартным первым товароведом равна 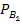 (A) = 0, 9, вторым -
(A) = 0, 9, вторым - 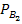 (A) = 0, 98.
(A) = 0, 98.
Вероятность того, что изделие будет признано стандартным по формуле полной вероятности равна
P(A)= P( 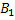 )
) 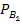 (A) + P(
(A) + P( 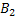 )
) 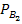 (A) = 0, 55 * 0, 9 + 0, 45 * 0, 98 = 0, 936
(A) = 0, 55 * 0, 9 + 0, 45 * 0, 98 = 0, 936
Искомая вероятность того, что изделие проверил второй товаровед, по формуле Бейеса равна
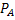 (
( 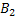 )= P(
)= P( 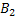 ) *
) * 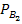 (A) / P(A)= 0, 45*0, 98 / 0, 936 = 0, 47.
(A) / P(A)= 0, 45*0, 98 / 0, 936 = 0, 47.
#103: По формуле Бейеса: i=1n∑ РА(Вi)= i=1n∑ Р(Вi)* РВi(А)/Р(А)=Р(А)/Р(А)=1 что и требовалось доказать.
#104Так как события 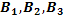 образуют полную группу, и
образуют полную группу, и 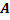 появится при условии появления лишь одного из них, то верно
появится при условии появления лишь одного из них, то верно 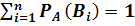 . Так как имеем
. Так как имеем 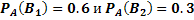 , то:
, то: 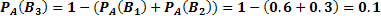
#105Решение:
Обозначим через А событие – в каждом из двух испытаний была извлечена стандартная деталь. Можно предположить, что B1 – детали извлекались из первой партии; B2 – детали извлекались из второй партии; В3 – детали извлекались из третей партии. Детали извлекались на удачу, поэтому вероятности предположений одинаковы: P(B1) = P(B2) = P(B3) = 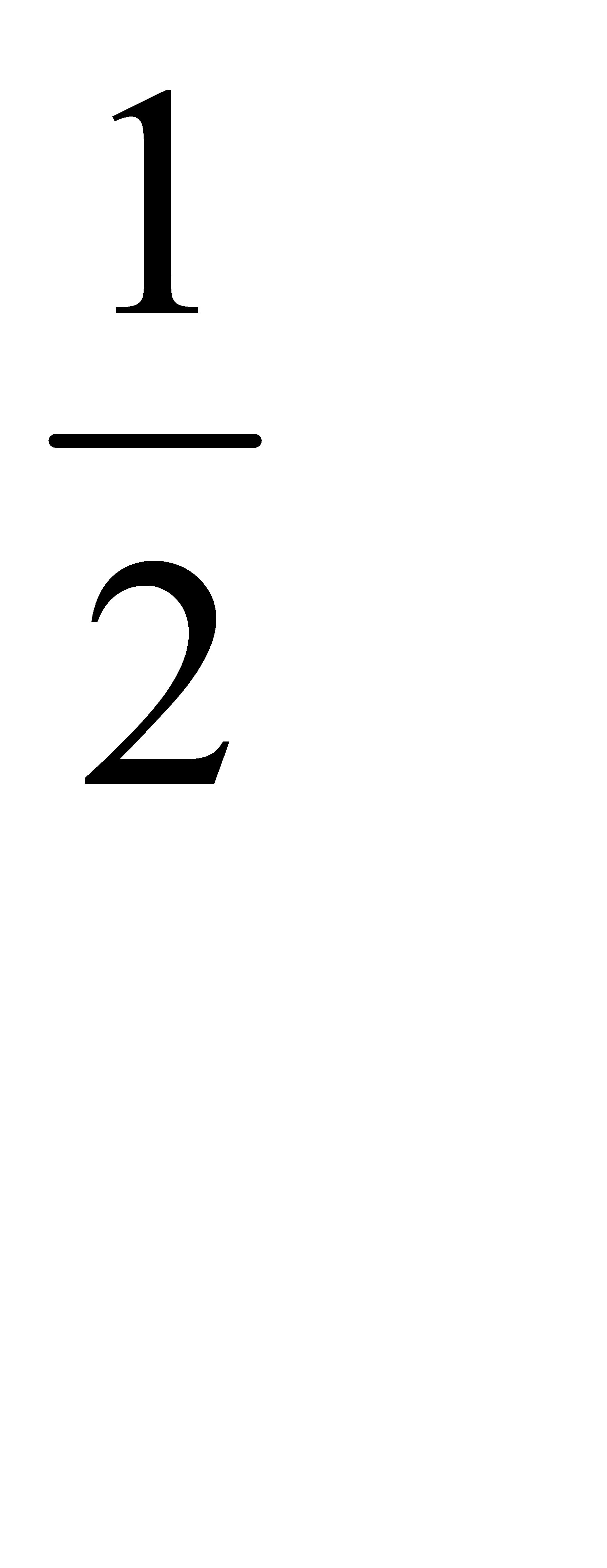
Вероятность того, что из первой партии будут последовательно извлечены две стандартные детали; поэтому 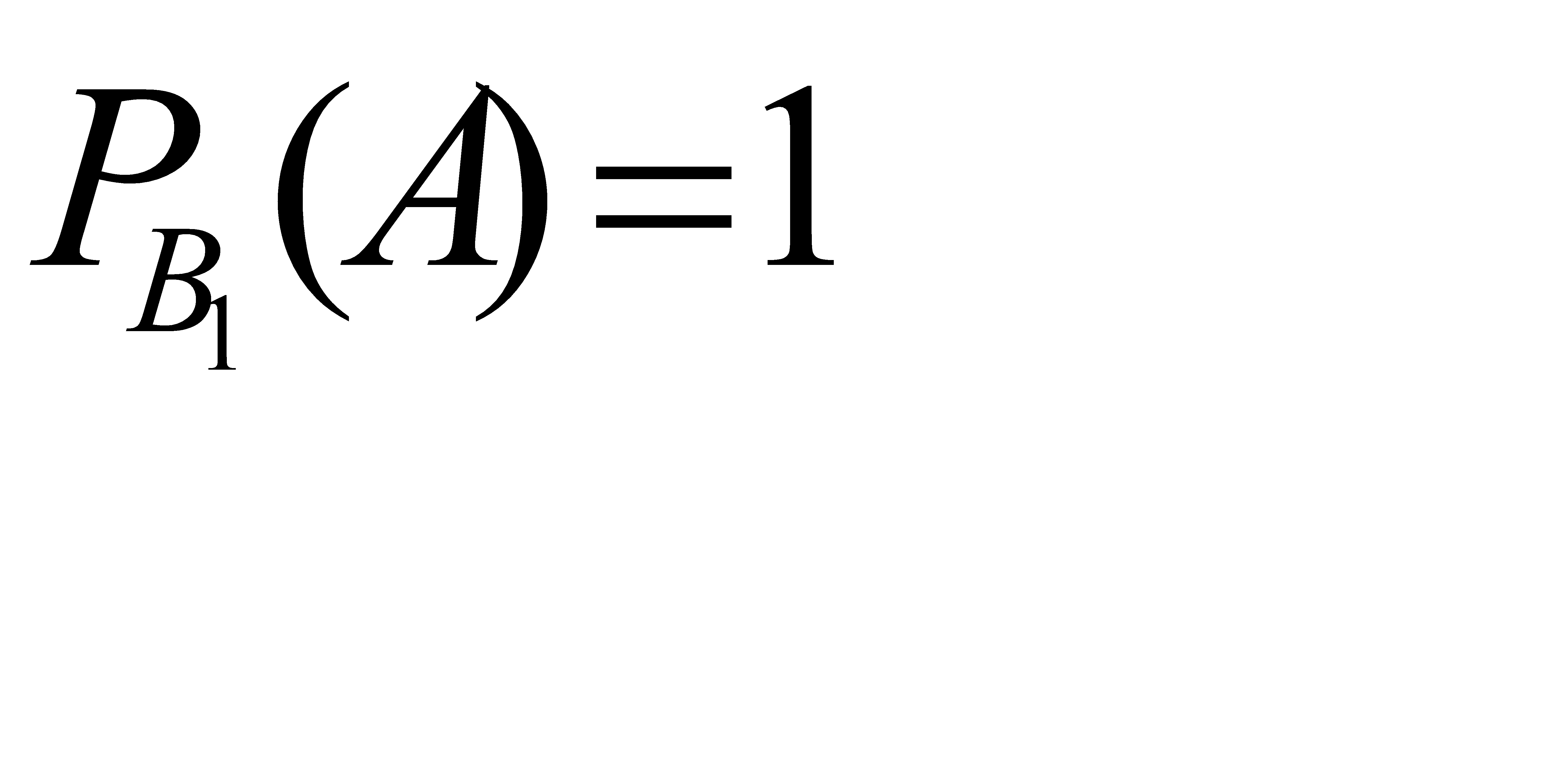 Условная вероятность
Условная вероятность 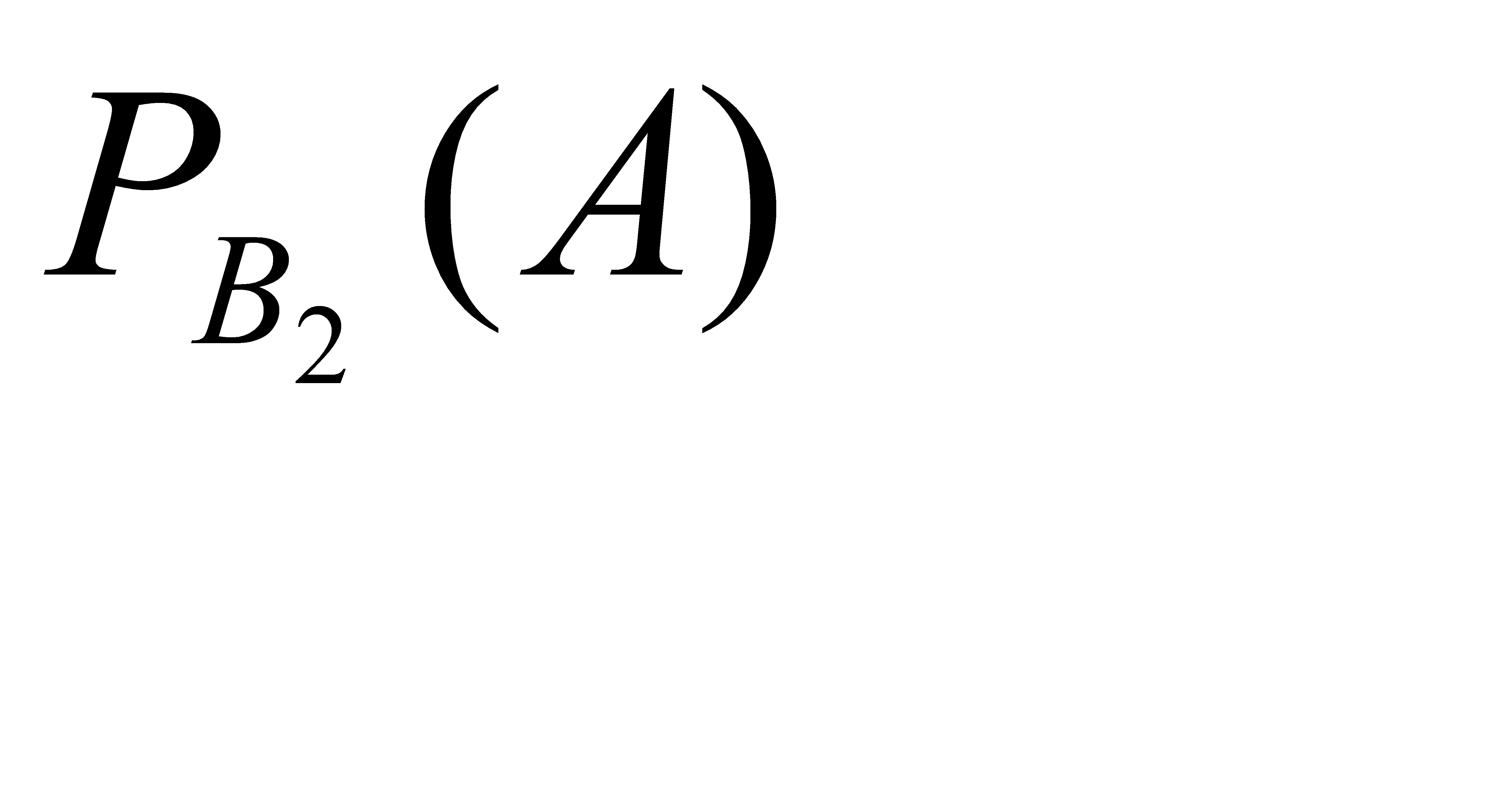 т. е вероятность того, что из второй партии будут извлечены две стандартные детали:
т. е вероятность того, что из второй партии будут извлечены две стандартные детали: 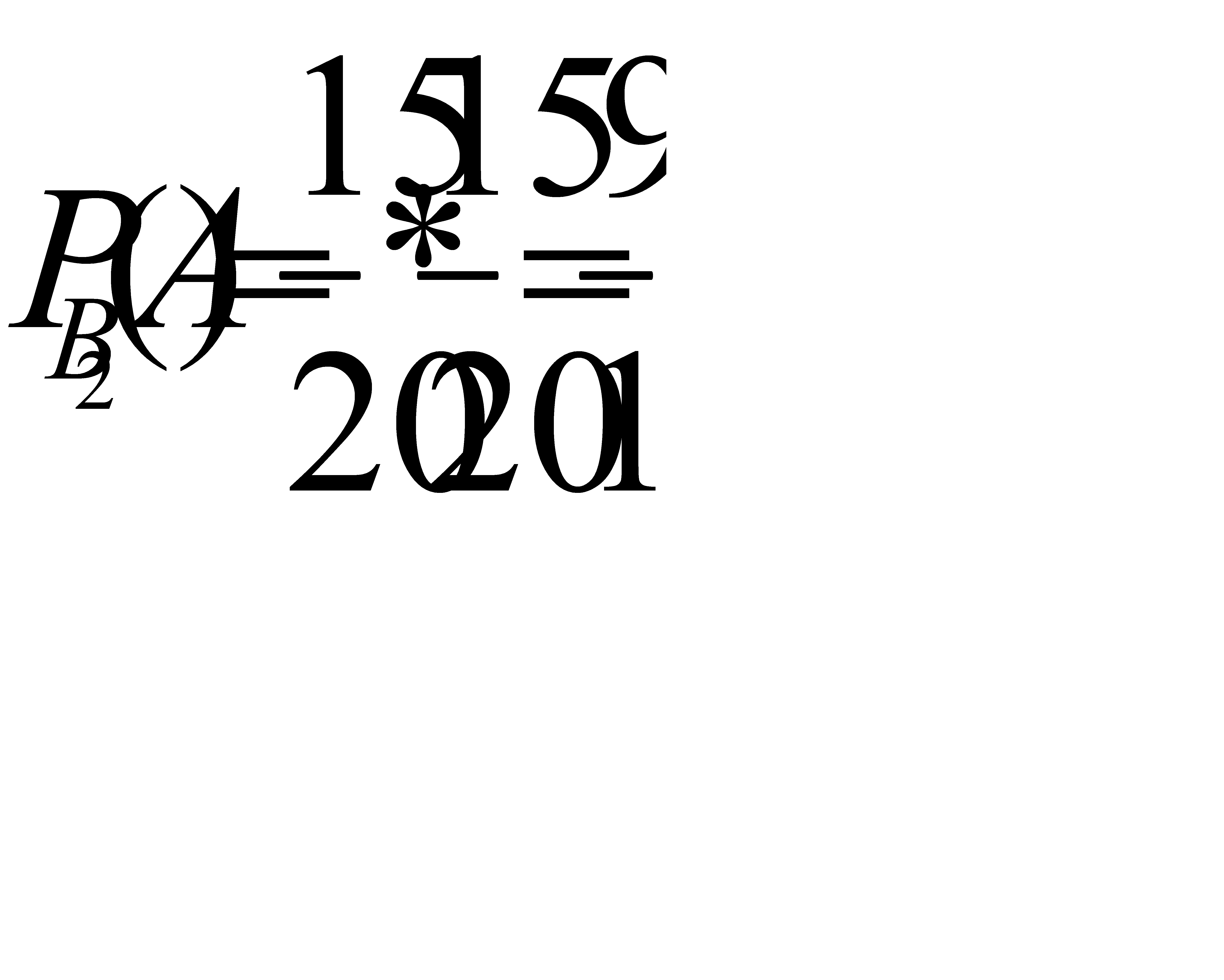 Найдем условную вероятность
Найдем условную вероятность 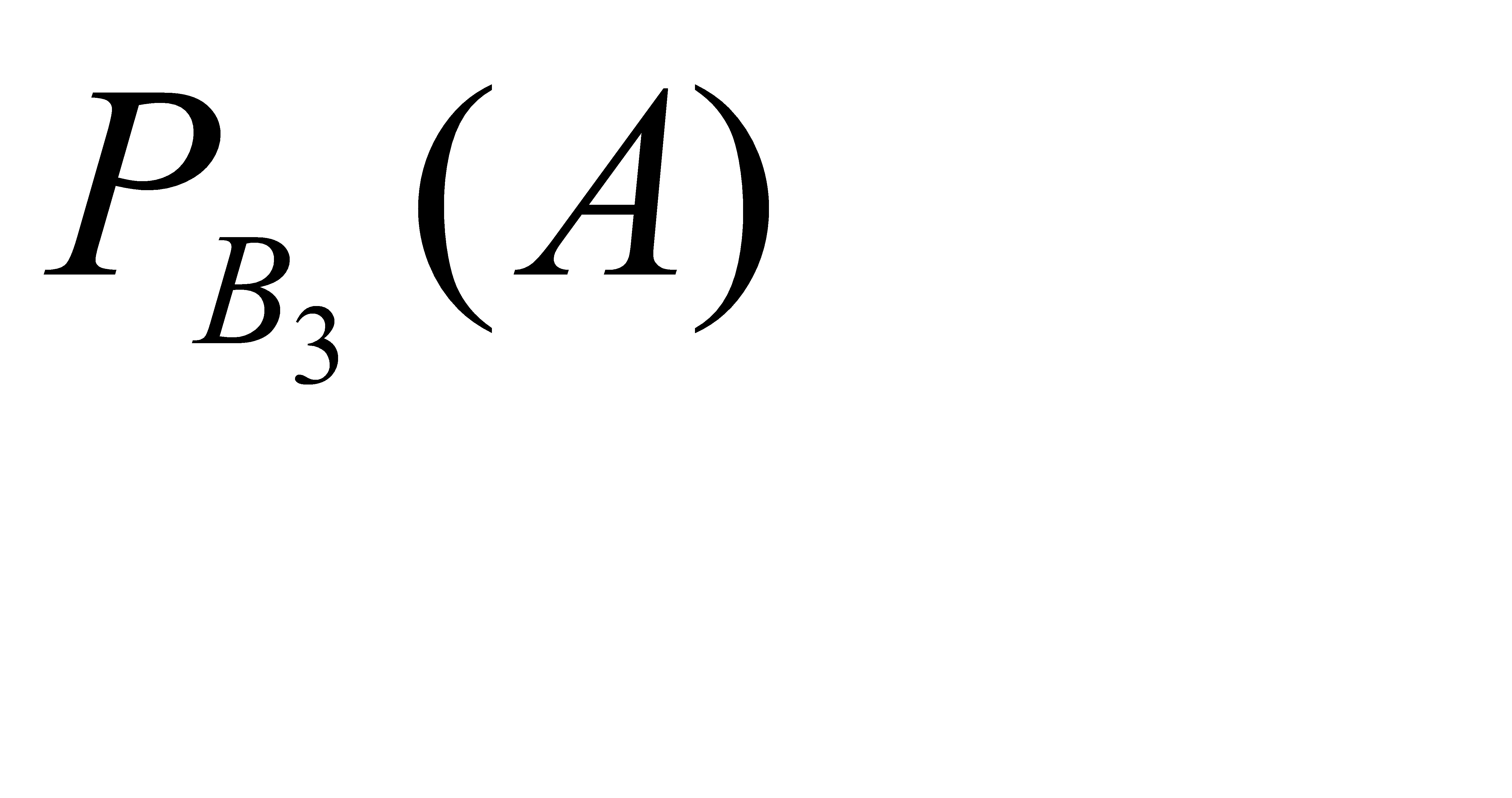 т. е вероятность того, что из третей партии будут последовательно извлечены две стандартные детали:
т. е вероятность того, что из третей партии будут последовательно извлечены две стандартные детали: 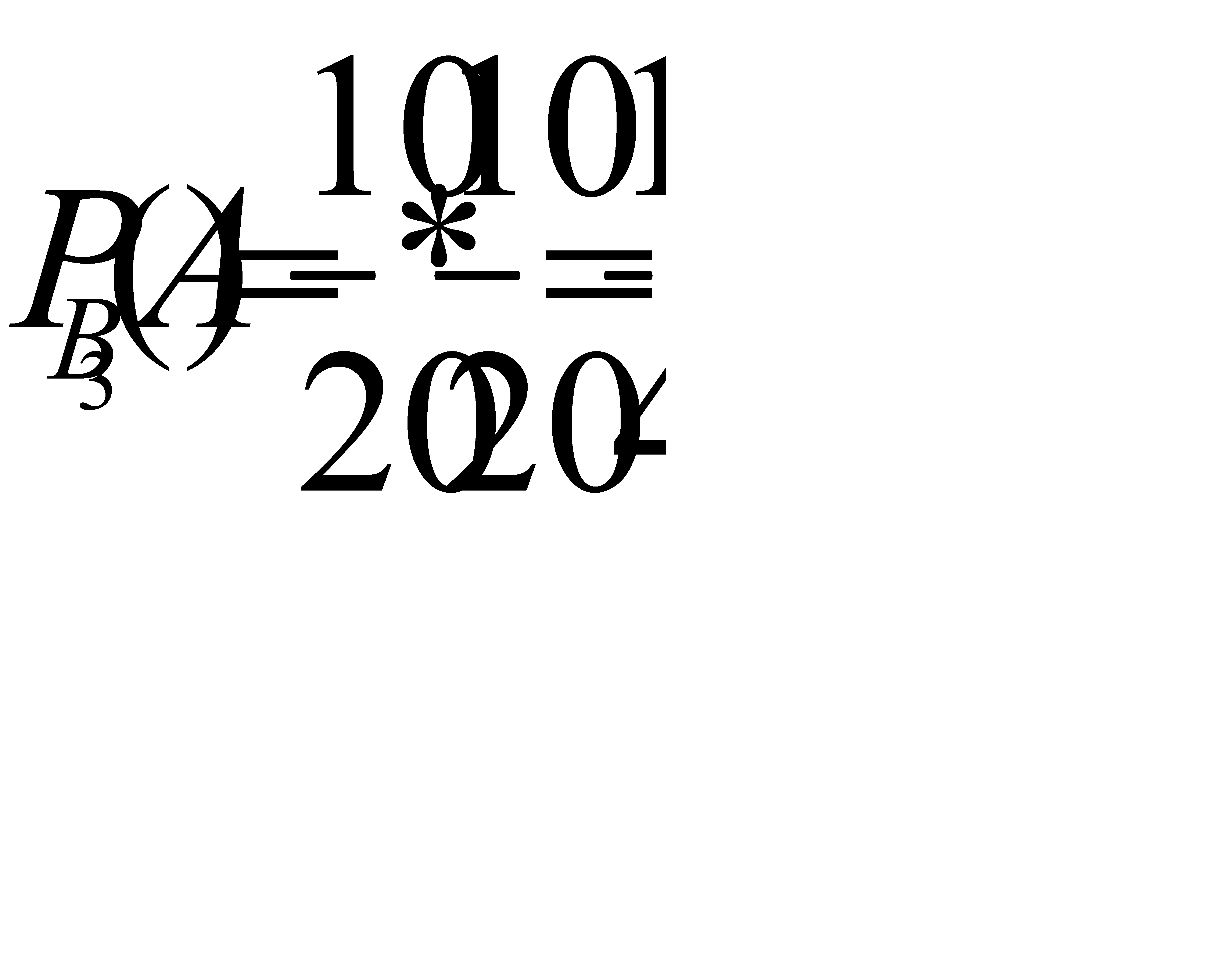
Искомая вероятность того, что обе извлеченные детали стандартные взяты из третей партии, по формуле Бейеса равна
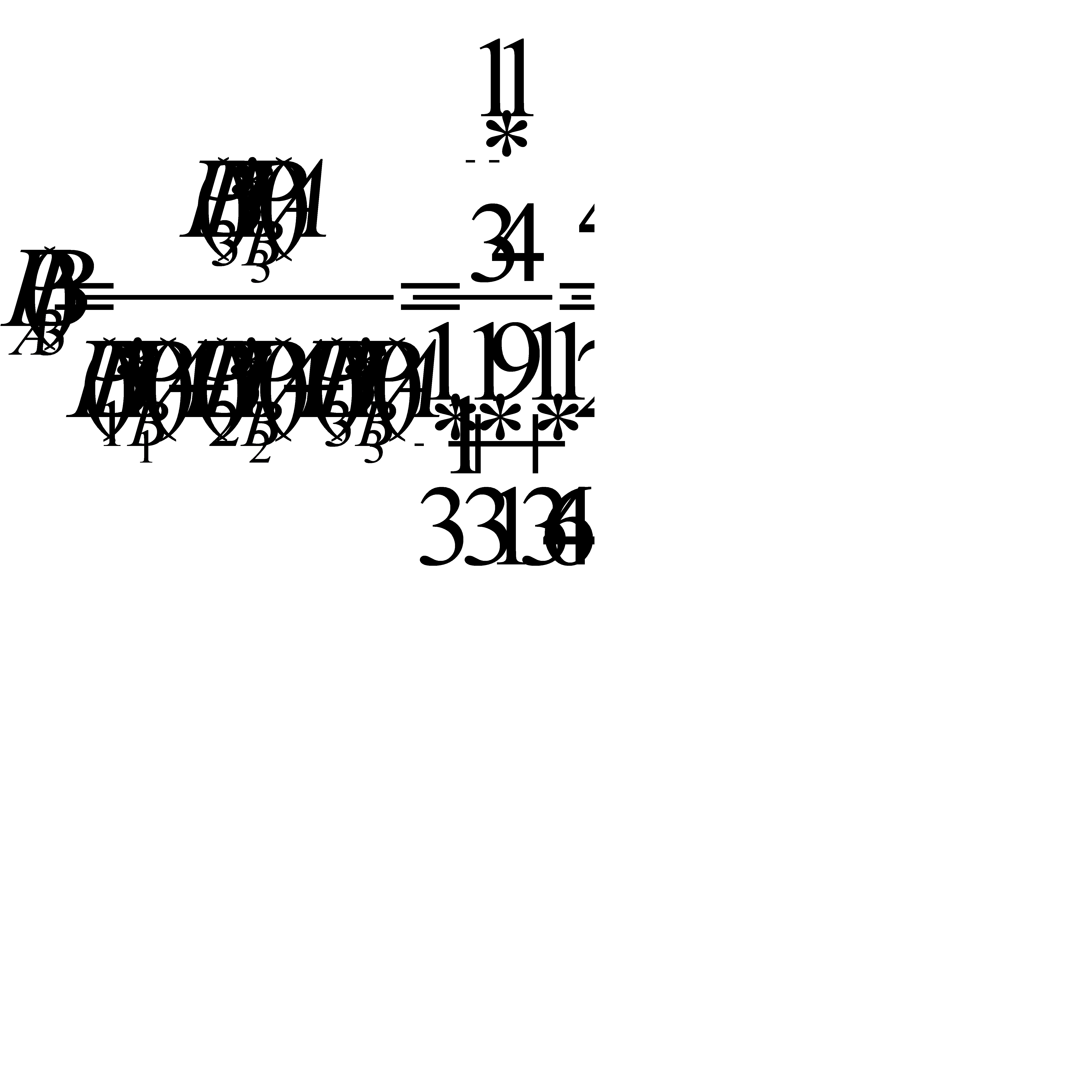 Ответ:
Ответ: 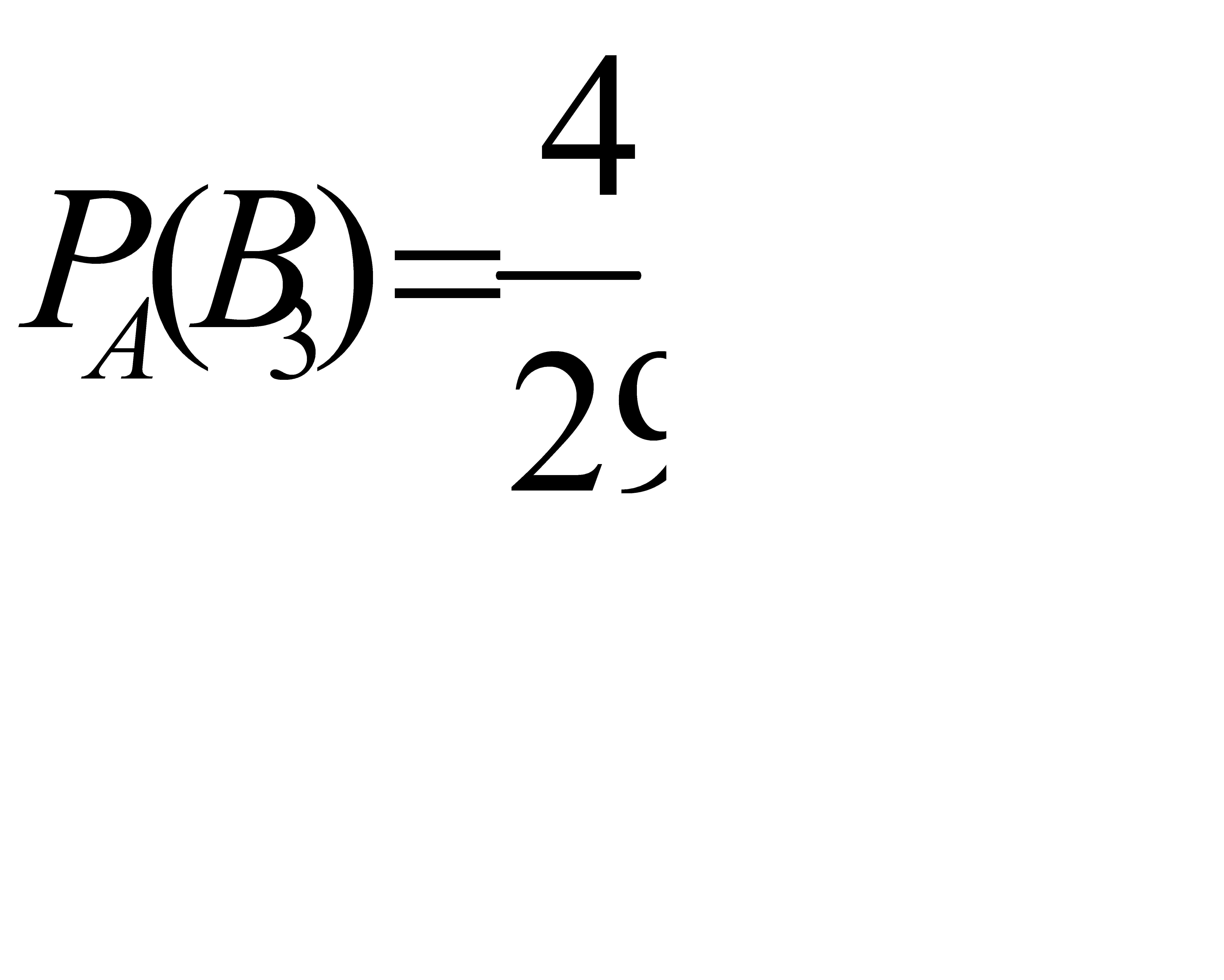
#106Обозначим через A событие- два орудия попали в цель. Сделаем два предположения:  - орудие не попало в цель.
- орудие не попало в цель.
По условию 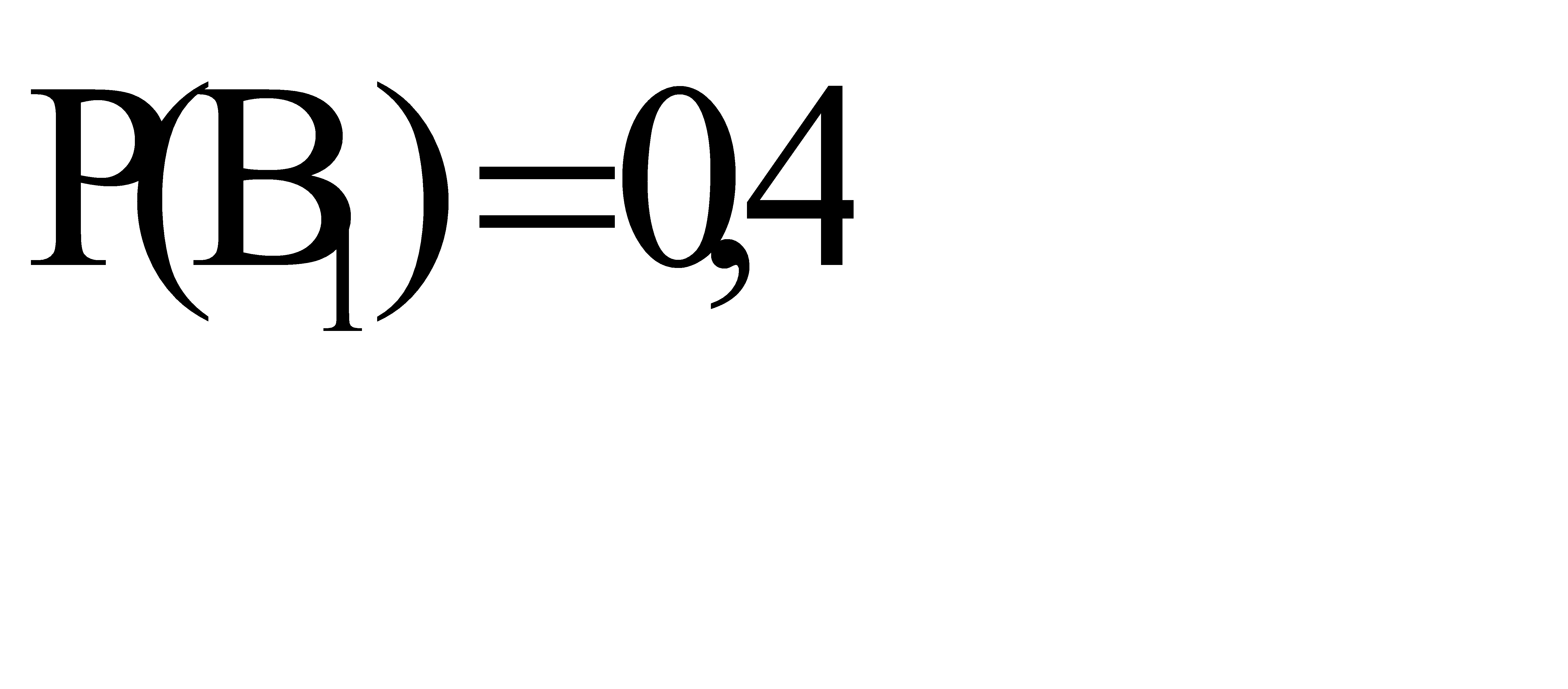 , следовательно
, следовательно 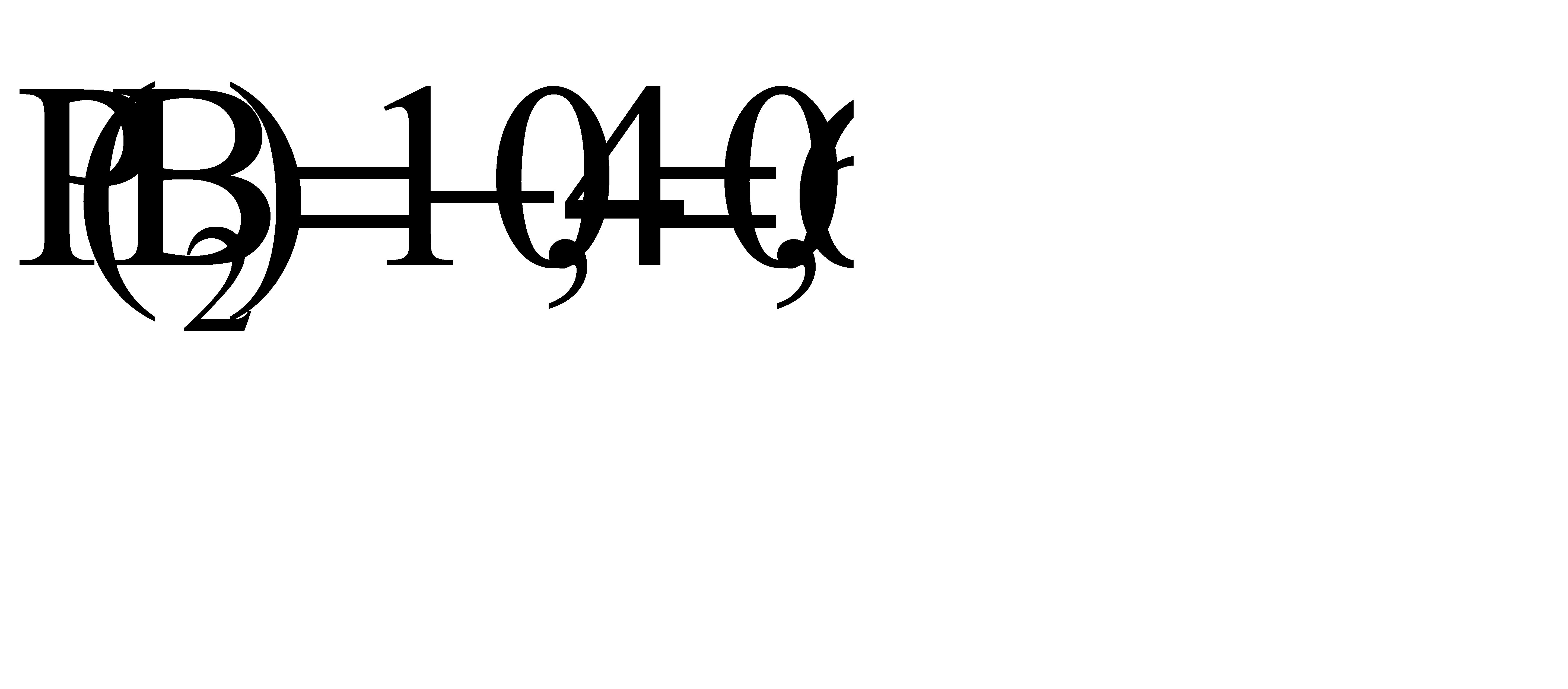
Найдем условную вероятность  , т. е. вероятность того, что в цель попало 2 снаряда, причем один из них послан первым орудием и, следовательно, второй - либо вторым орудием, либо третьим. Эти два события несовместны, поэтому применима теорема сложения:
, т. е. вероятность того, что в цель попало 2 снаряда, причем один из них послан первым орудием и, следовательно, второй - либо вторым орудием, либо третьим. Эти два события несовместны, поэтому применима теорема сложения:
 . Найдем условную вероятность
. Найдем условную вероятность  , т. е. вероятность того, что в цель попало два снаряда, причем первое орудие дало промах. Другими словами найдем вероятность того, что второе и третье орудие попали в цель. Эти два события независимы, поэтому применима теорема умножения:
, т. е. вероятность того, что в цель попало два снаряда, причем первое орудие дало промах. Другими словами найдем вероятность того, что второе и третье орудие попали в цель. Эти два события независимы, поэтому применима теорема умножения:  Искомая вероятность того, что первое орудие дало попадание, по формуле Бейеса равна:
Искомая вероятность того, что первое орудие дало попадание, по формуле Бейеса равна:  . Ответ:
. Ответ: 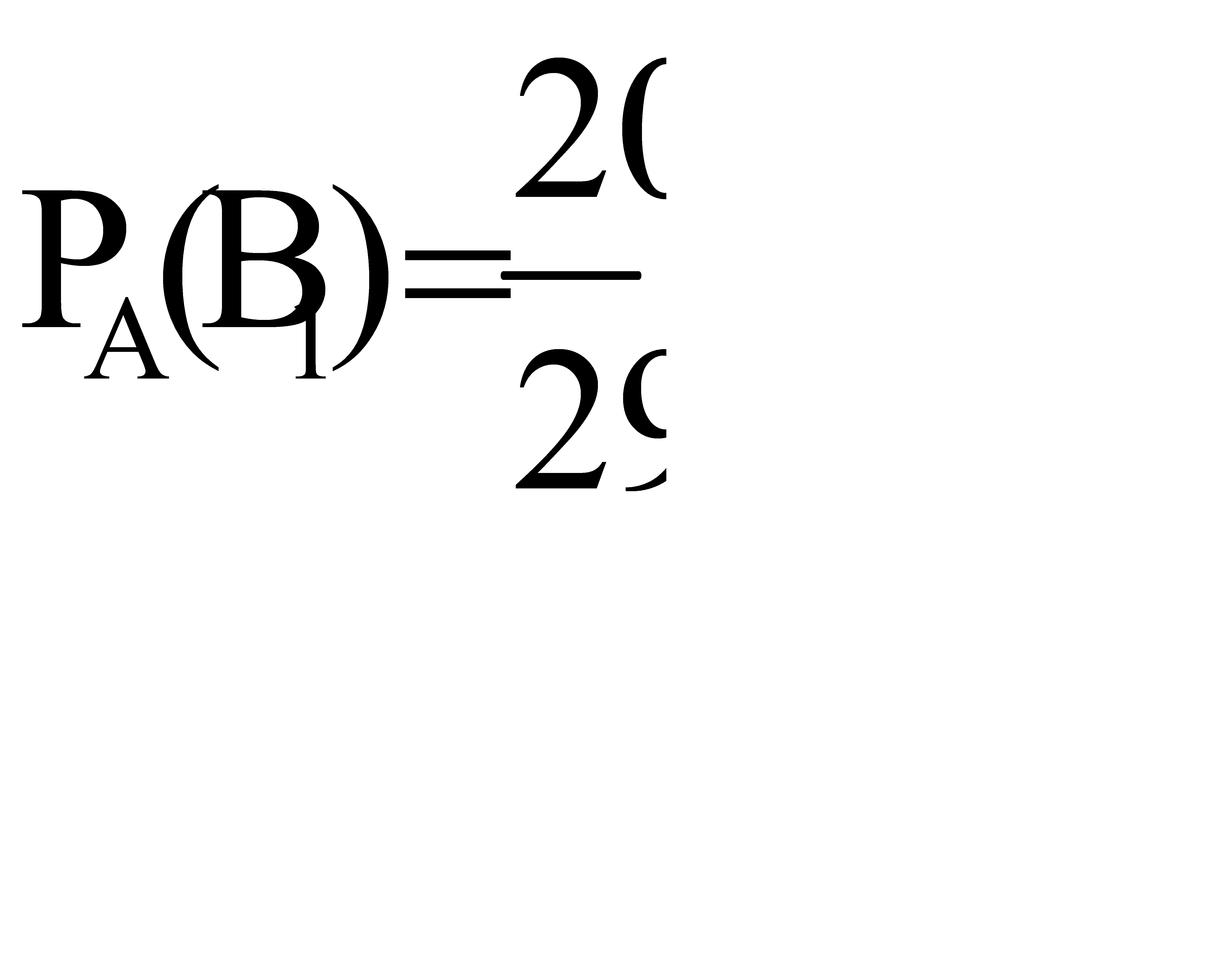
#107Решение. Обозначим через А событие – две пули поразили мишень. Сделаем два предположения (гипотезы): В1 – третий стрелок поразил мишень; В2 – третий стрелок не попал в мишень.
По условию, Р(В1) = 0, 4; следовательно (событие В2 противоположно событию В1), Р(В2) = 1 – 0, 4 = 0, 6.
Найдем условную вероятность РВ1(А), т. е. вероятность того, что мишень поразили две пули, причем одна из них принадлежит третьему стрелку и, следовательно, вторая – либо первому стрелку (при этом второй не попал), либо второму стрелку (при этом первый не попал). Эти два события несовместны, поэтому применима теорема сложения:
РВ1(А) = p1∙ q2 + p2∙ q1 = 0, 6∙ 0, 5 + 0, 5∙ 0, 4 = 0, 5.
Найдем условную вероятность РВ2(А), т. е. вероятность того, что мишень поразили две пули, причем третий стрелок промахнулся. Другими словами, найдем вероятность того, что первый и второй стрелки поразили мишень. Эти два события независимы, поэтому применима теорема умножения: РВ2(А) = p1∙ p2 = 0, 6∙ 0, 5 = 0, 3.
Искомая вероятность того, что третий стрелок поразил мишень, по формуле Бейеса равна
РА(В1) = Р(В1)∙ РВ1(А)/[ Р(В1)∙ РВ1(А) + Р(В2)∙ РВ2(А)] = 0, 4∙ 0, 5/( 0, 4∙ 0, 5 + 0, 6∙ 0, 3 ) = 10/19. Ответ: 10/19.
#108 Обозначим через А событие – отказали два элемента. Можно сделать следующие предположения (гипотезы):
В1 - отказали первый и второй элементы, а третий элемент исправен, причем (поскольку элементы работают независимо, применима теорема умножения)Р(В1) = p1∙ p2∙ q3 = 0, 2∙ 0, 4∙ 0, 7 = 0, 056; В2 - отказали первый и третий элементы, а второй элемент исправен, причемР(В2) = p1∙ p3∙ q2 = 0, 2∙ 0, 3∙ 0, 6 = 0, 036; В3 - отказали второй и третий элементы, а первый - исправен, причемР(В3) = p2∙ p3∙ q1 = 0, 4∙ 0, 3∙ 0, 8 = 0, 096; В4 - отказал только один элемент; В5 - отказали все три элемента; В6 - ни один из элементов не отказал. Вероятности последних трех гипотез не вычислены, так как при этих гипотезах событие А (отказали два элемента) невозможно и значит условные вероятности РВ4(А), РВ5(А) и РВ6(А) равны нулю, следовательно, равны нулю и произведения Р(В4)∙ РВ4(А), Р(В5)∙ РВ5(А) и Р(В6)∙ РВ6(А) при любых значениях вероятностей гипотез В4, В5 и В6.
Поскольку при гипотезах В1, В2 и В3 событие А достоверно, то соответствующие условные вероятности равны единице:
РВ1(А) = РВ2(А) = РВ3(А) = 1. По формуле полной вероятности, вероятность того, что отказали два элемента, равна
Р(А) = Р(В1)∙ РВ1(А) + Р(В2)∙ РВ2(А) + Р(В3)∙ РВ3(А) + Р(В4)∙ РВ4(А) + Р(В5)∙ РВ5(А) + Р(В6)∙ РВ6(А) = 0, 056 + 0, 036 + 0, 096 = 0, 188. По формуле Бейеса, искомая вероятность того, что отказали первый и второй элементы,
РА(В1) = Р(В1)∙ РВ1(А)/ Р(А) = 0, 056/0, 188 = 0, 3. Ответ: 0, 3.
#109 Обозначим через А событие – отказали две лампы. Можно сделать следующие предположения (гипотезы):
В1 - отказали первая и вторая лампы, а третья и четвертая лампы исправны, причем (поскольку лампы работают независимо, применима теорема умножения)Р(В1) = p1∙ p2∙ q3∙ q4 = 0, 1∙ 0, 2∙ 0, 7∙ 0, 6 = 0, 0084; В2 - отказали первая и третья лампы, а вторая и четвертая исправны, причемР(В2) = p1∙ q2∙ p3 ∙ q4 = 0, 1∙ 0, 8∙ 0, 3∙ 0, 6 = 0, 0144; В3 - отказали первая и четвертая лампы, а вторая и третья - исправны, причемР(В3) = p1∙ q2∙ q3∙ p4 = 0, 1∙ 0, 8∙ 0, 7∙ 0, 4 = 0, 0224; В4 - отказали вторая и третья лампы, а первая и четвертая - исправны, причемР(В4) = q1∙ p2∙ p3∙ q4 = 0, 9∙ 0, 2∙ 0, 3∙ 0, 6 = 0, 0324;
В5 - отказали вторая и четвертая лампы, а первая и третья - исправны, причемР(В5) = q1∙ p2∙ q3∙ p4 = 0, 9∙ 0, 2∙ 0, 7∙ 0, 4 = 0, 0504;
В6 - отказали третья и четвертая лампы, а первая и вторая - исправны, причемР(В6) = q1∙ q2∙ p3∙ p4 = 0, 9∙ 0, 8∙ 0, 3∙ 0, 4 = 0, 0864;
В7 – отказала только одна лампа; В8 - отказали три лампы; В9 - отказали все четыре лампы и В10 – все лампы остались исправны. Вероятности последних четырех гипотез не вычислены, так как при этих гипотезах событие А (отказали две лампы) невозможно и значит условные вероятности РВ7(А), РВ8(А), РВ9(А) и РВ10(А) равны нулю, следовательно, равны нулю и произведения Р(В7)∙ РВ7(А), Р(В8)∙ РВ8(А), Р(В9)∙ РВ9(А) и Р(В10)∙ РВ10(А) при любых значениях вероятностей гипотез В7, В8, В9 и В10.
Поскольку при гипотезах В1 – В6 событие А достоверно, то соответствующие условные вероятности равны единице:
РВ1(А) = РВ2(А) = РВ3(А) = РВ4(А) = РВ5(А) = РВ6(А) = 1.
По формуле полной вероятности, вероятность того, что отказали две лампы, равна
Р(А) = Р(В1)∙ РВ1(А) + Р(В2)∙ РВ2(А) + Р(В3)∙ РВ3(А) + Р(В4)∙ РВ4(А) + Р(В5)∙ РВ5(А) + Р(В6)∙ РВ6(А) + Р(В7)∙ РВ7(А) + Р(В8)∙ РВ8(А) + Р(В9)∙ РВ9(А) + Р(В10)∙ РВ10(А) = 0, 0084 + 0, 0144 + 0, 0224 + 0, 0324 + 0, 0504 + 0, 0864 = 0, 2144.
По формуле Бейеса, искомая вероятность того, что отказали первая и вторая лампы, равнаРА(В1) = Р(В1)∙ РВ1(А)/ Р(А) = 0, 0084/0, 2144 ~ 0, 039. Ответ: 0, 039.
#110Играют равносильные шахматисты, поэтому вероятность выигрыша p=1/2; следовательно, вероятность проигрыша q также равна 1/2. Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли. Найдем вероятность того, что две партии из четырех будут выиграны: 
найдем вероятность того, что выиграны три партии из шести:  Так как P4(2)> P6(3), то вероятнее выиграть две партии из четырех, чем три из шести.
Так как P4(2)> P6(3), то вероятнее выиграть две партии из четырех, чем три из шести.
#111Играют равносильные шахматисты, поэтому вероятность выигрыша 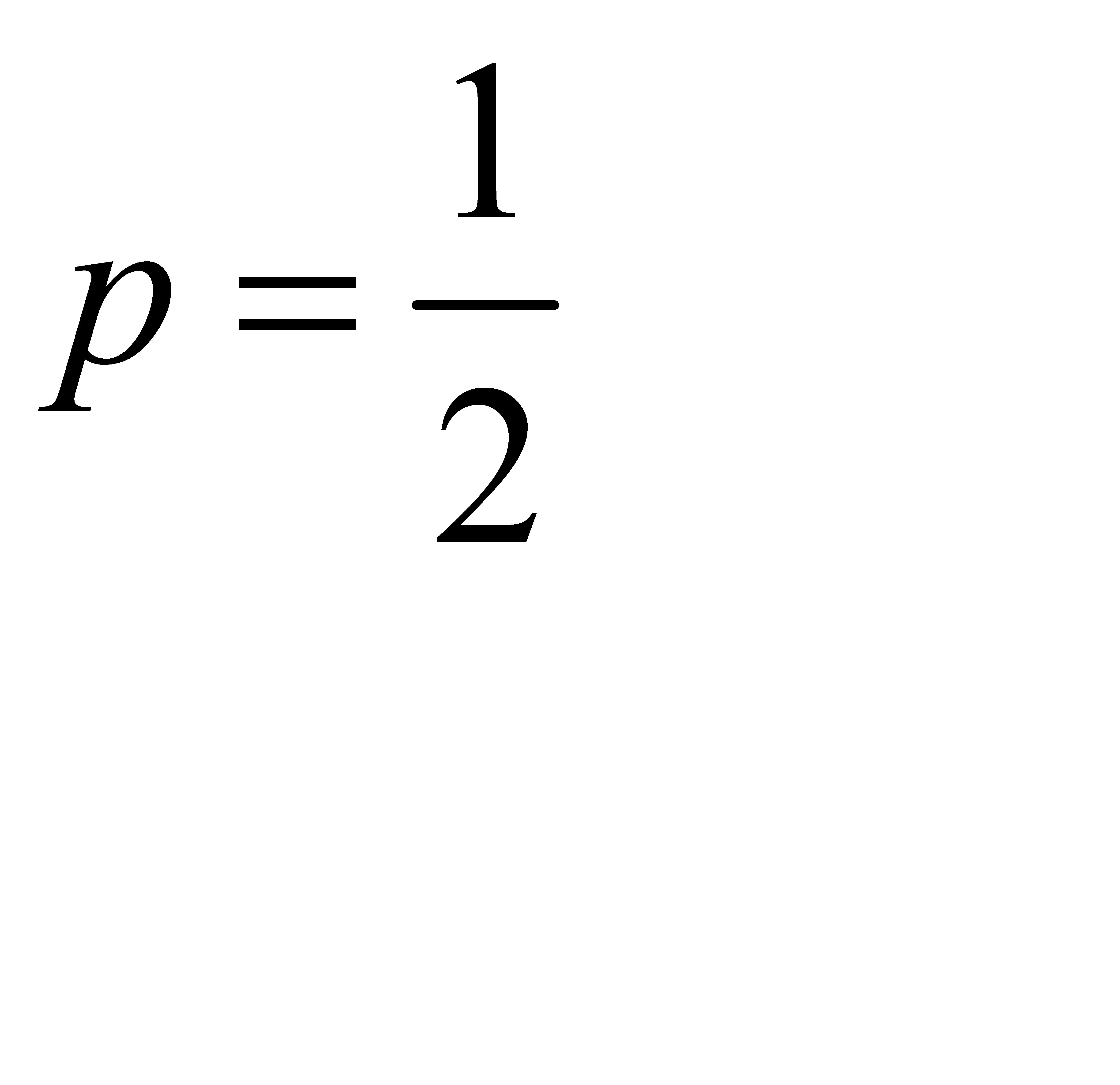 ; следовательно, вероятность проигрыша
; следовательно, вероятность проигрыша 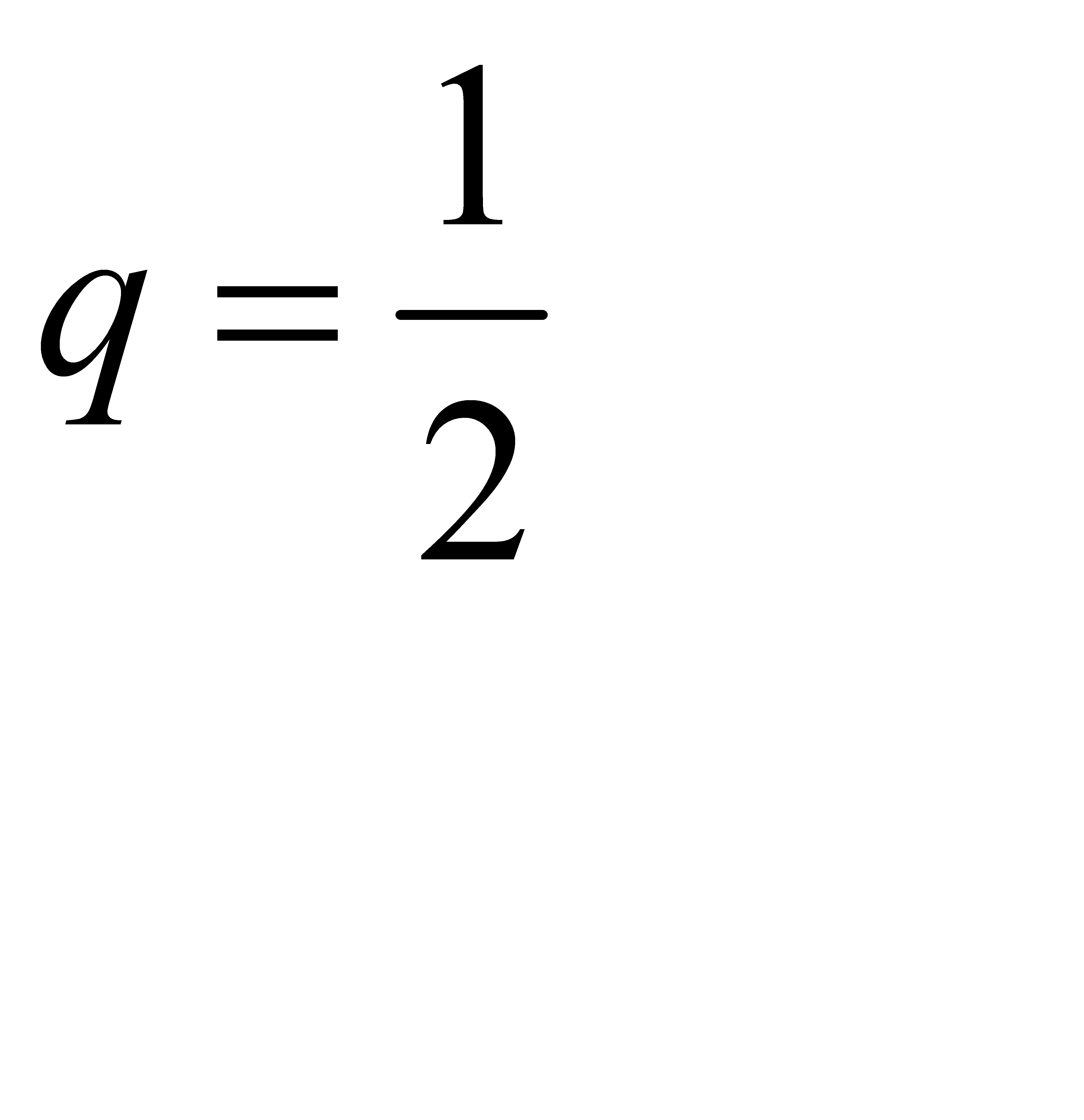 . Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выигранв партии, то применима формула Бернулли. А) Найдем вероятность того, что две партии из четырех будут выиграны:
. Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выигранв партии, то применима формула Бернулли. А) Найдем вероятность того, что две партии из четырех будут выиграны: 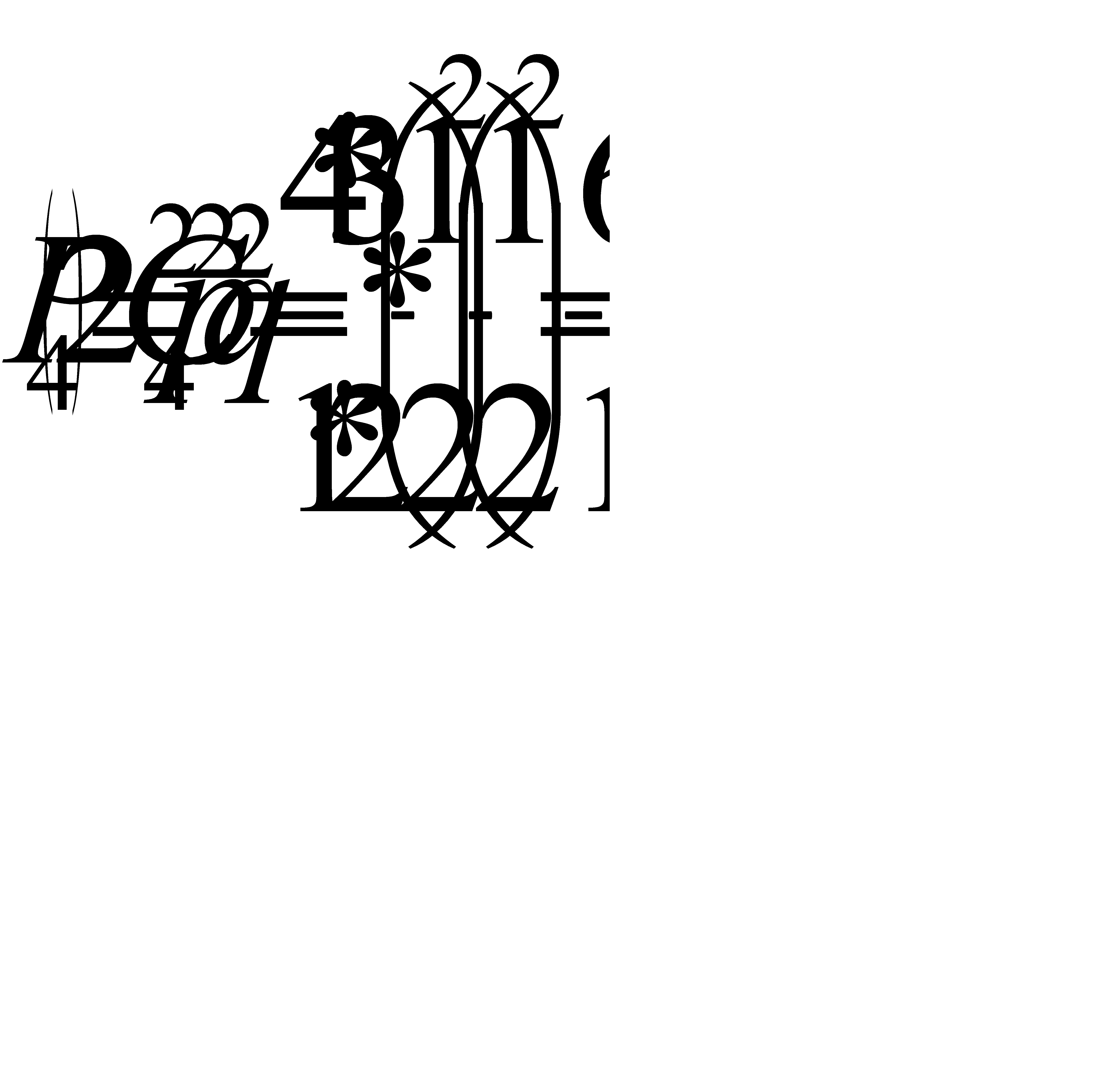 Найдем вероятность того, что одна партия из двух будет выиграна:
Найдем вероятность того, что одна партия из двух будет выиграна:  Б) Найдем вероятность выиграть не менее двух партий из четырех:
Б) Найдем вероятность выиграть не менее двух партий из четырех:  Найдем вероятность выиграть не менее трех партий из пяти:
Найдем вероятность выиграть не менее трех партий из пяти: 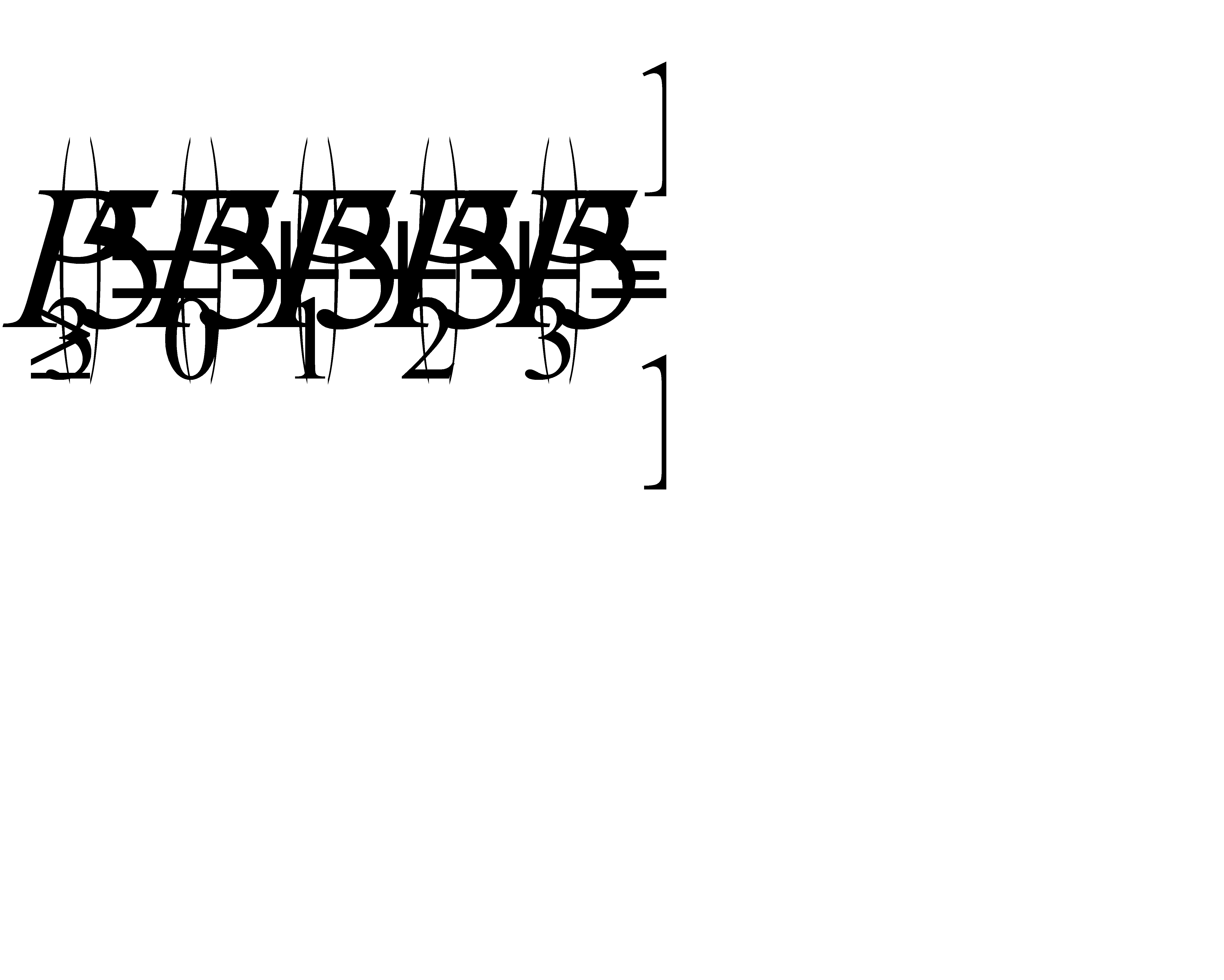
#112При бросании монеты вероятность выпадения герба и решки, равновероятны, поэтому вероятность выпадения герба равна 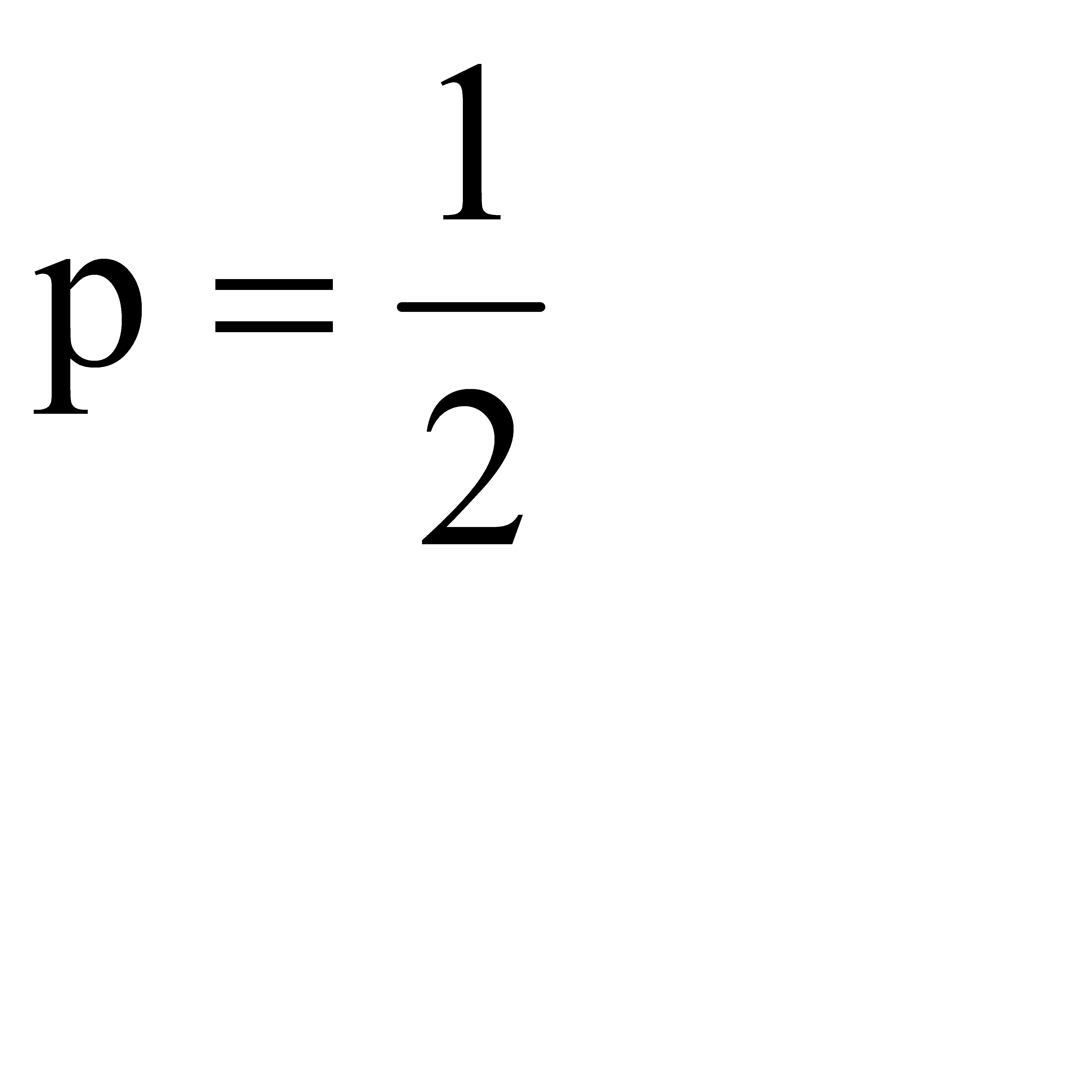 ; следовательно вероятность выпадения решки
; следовательно вероятность выпадения решки 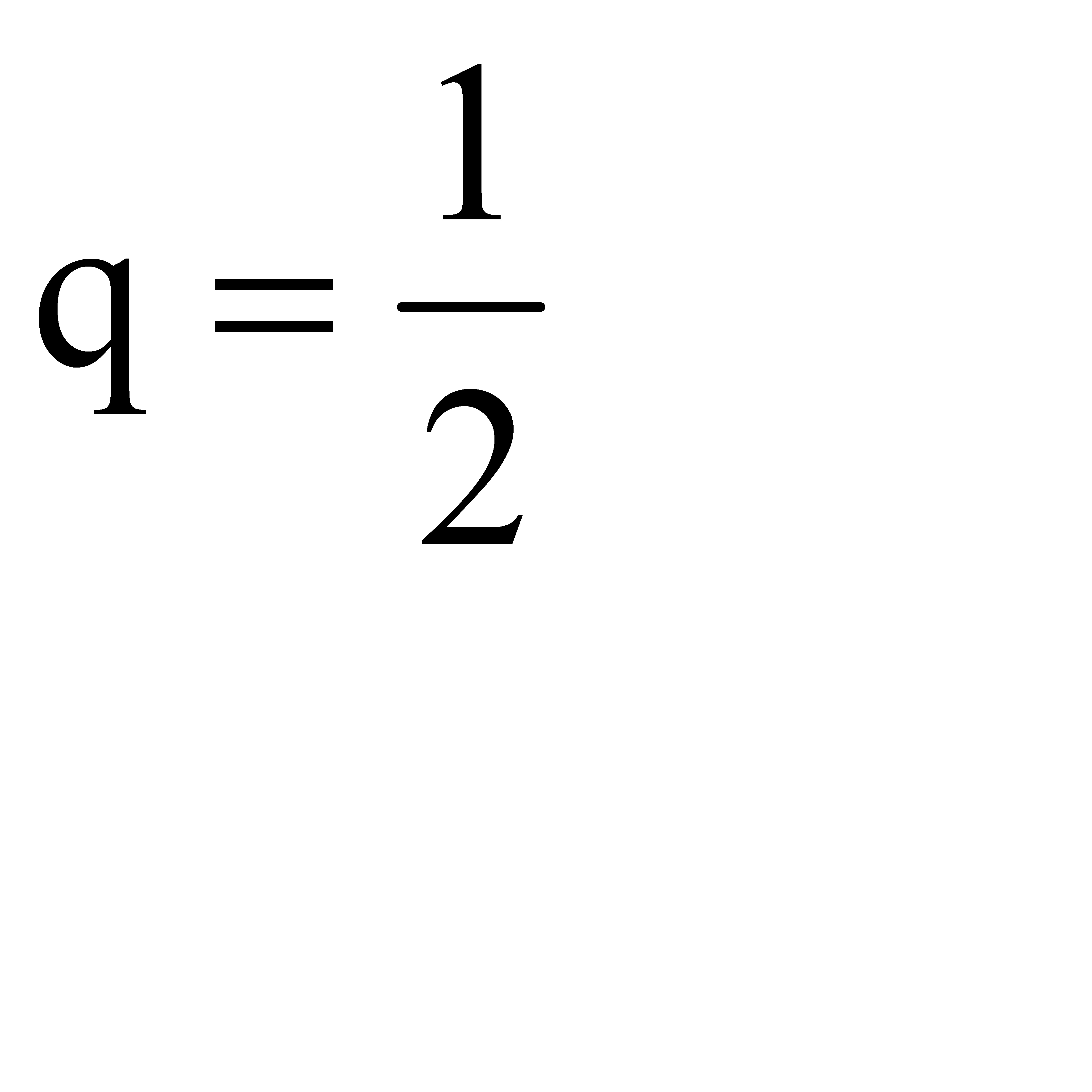 ; Так как при бросании вероятность постоянна, то применима формула Бернулли. А) Найдем вероятность того, что герб выпадет менее двух раз:
; Так как при бросании вероятность постоянна, то применима формула Бернулли. А) Найдем вероятность того, что герб выпадет менее двух раз:  ;
;
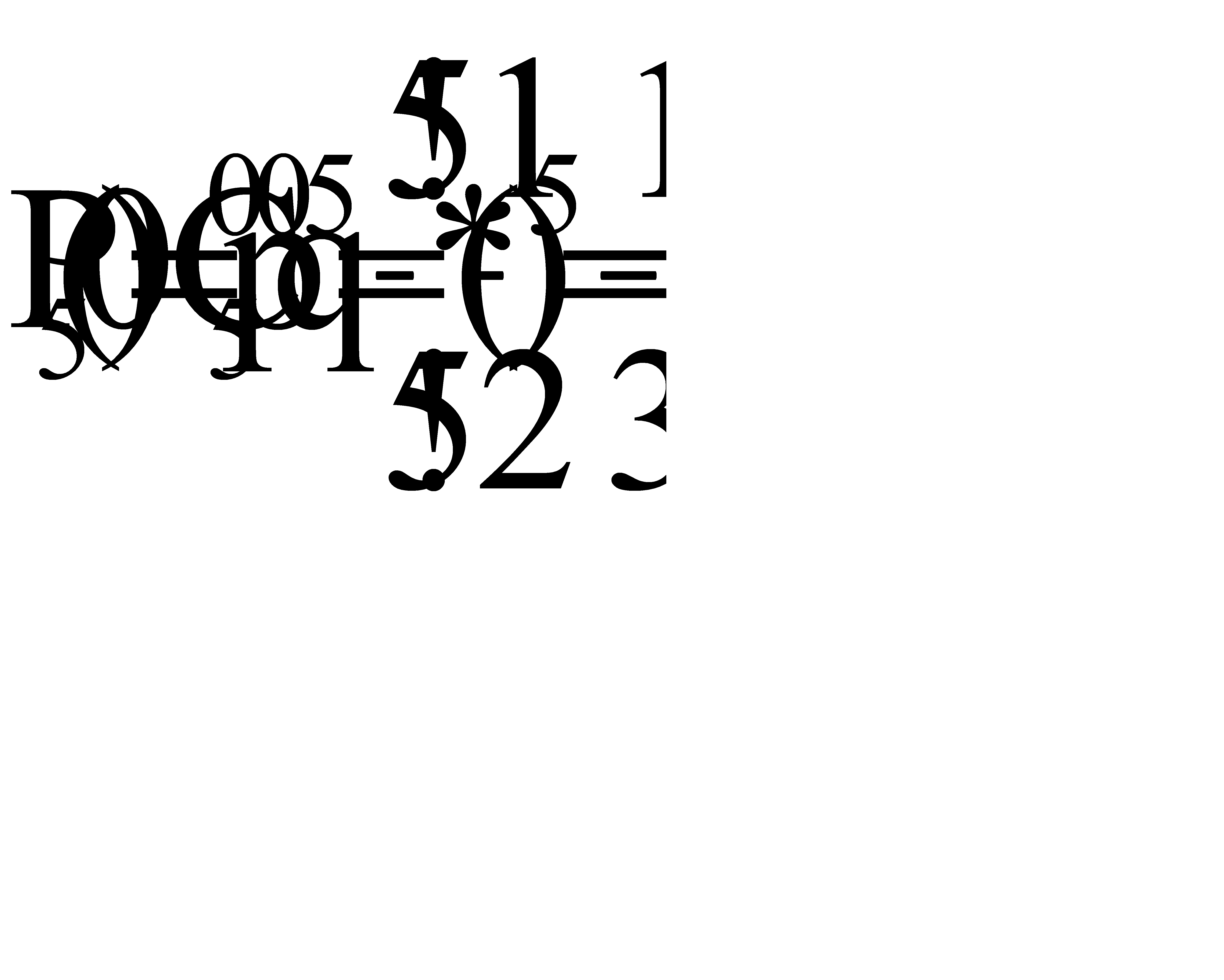 .
. 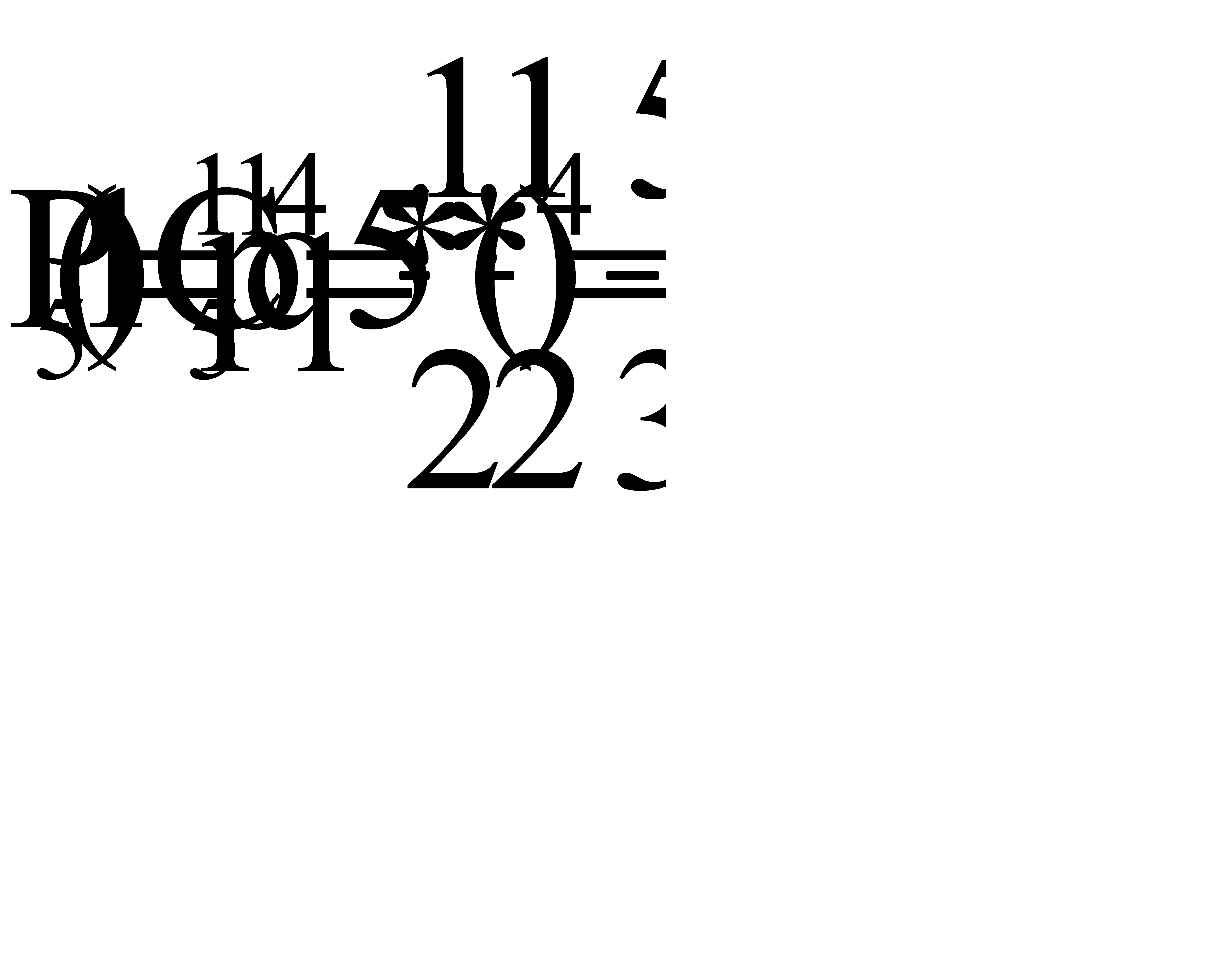
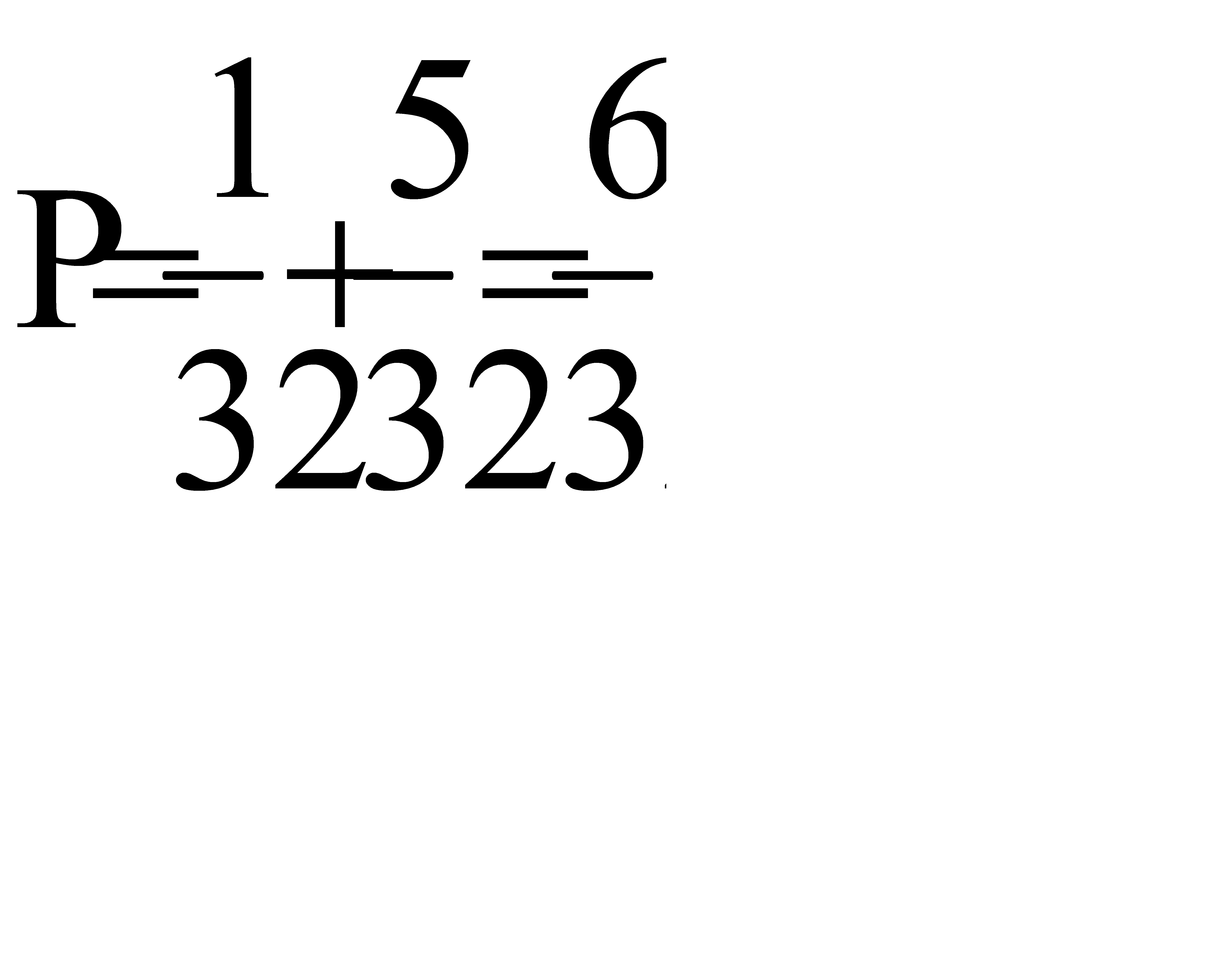 .
.
Б) Найдем вероятность того, что герб выпадет не менее двух раз:  ;
;
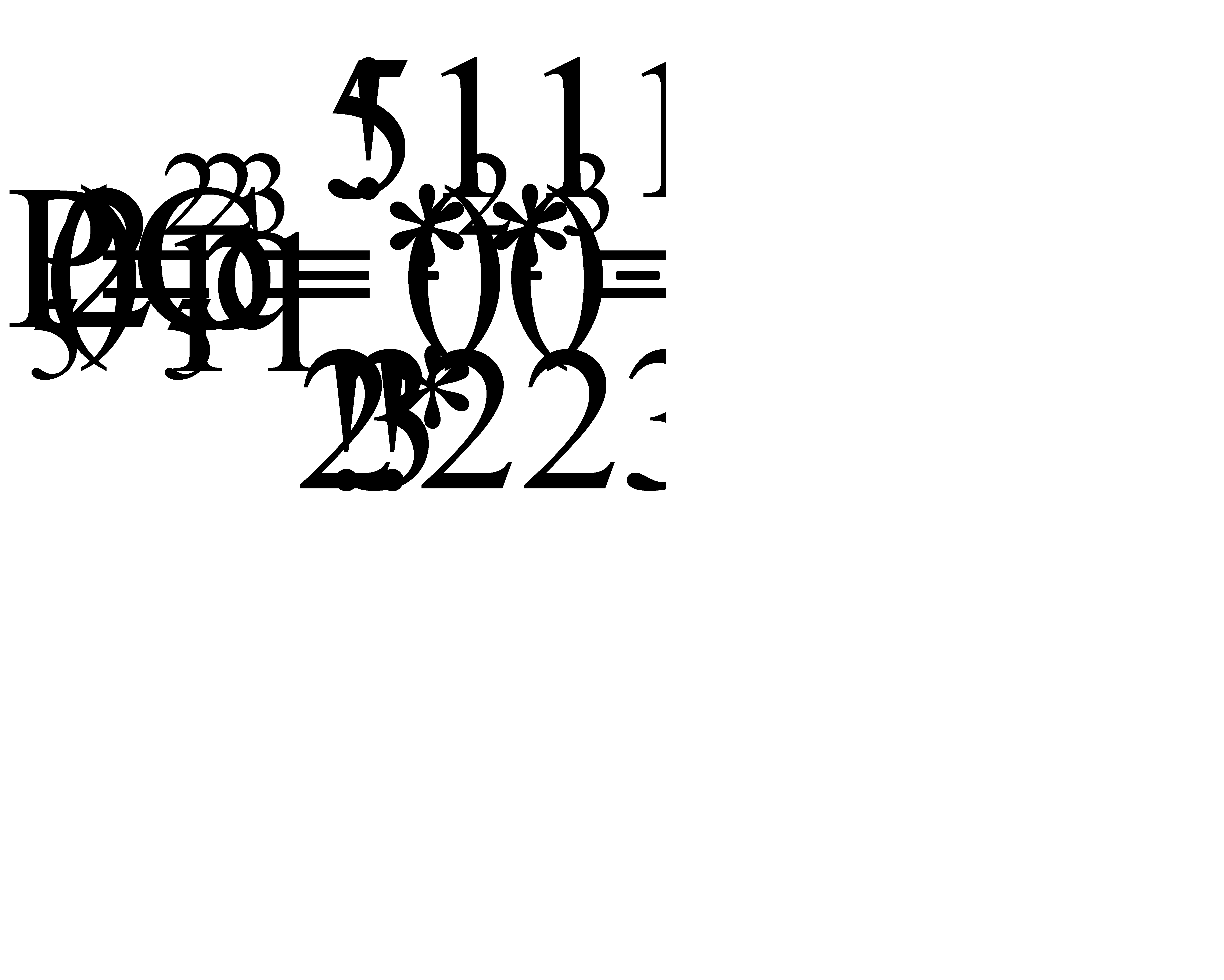 ,
, 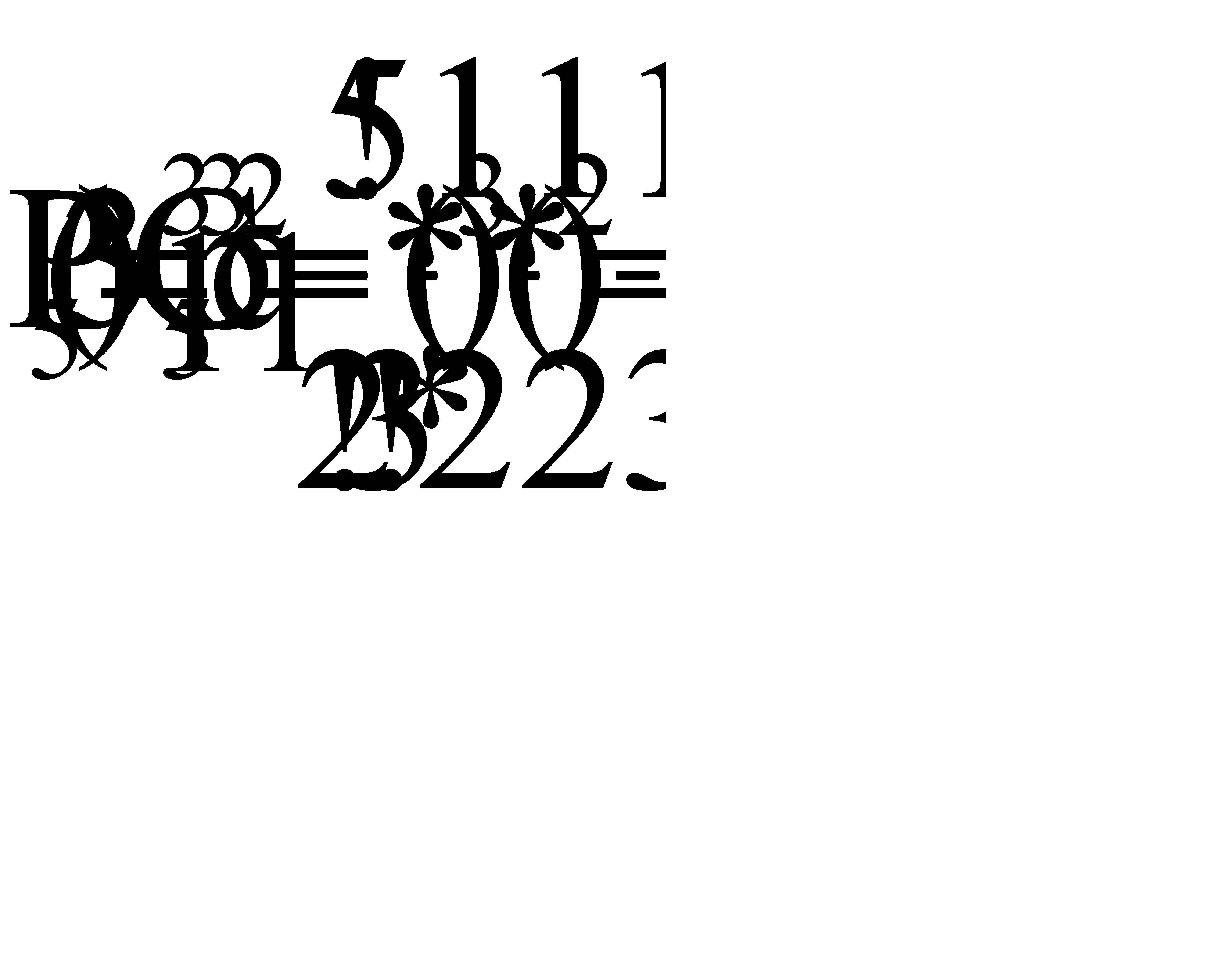
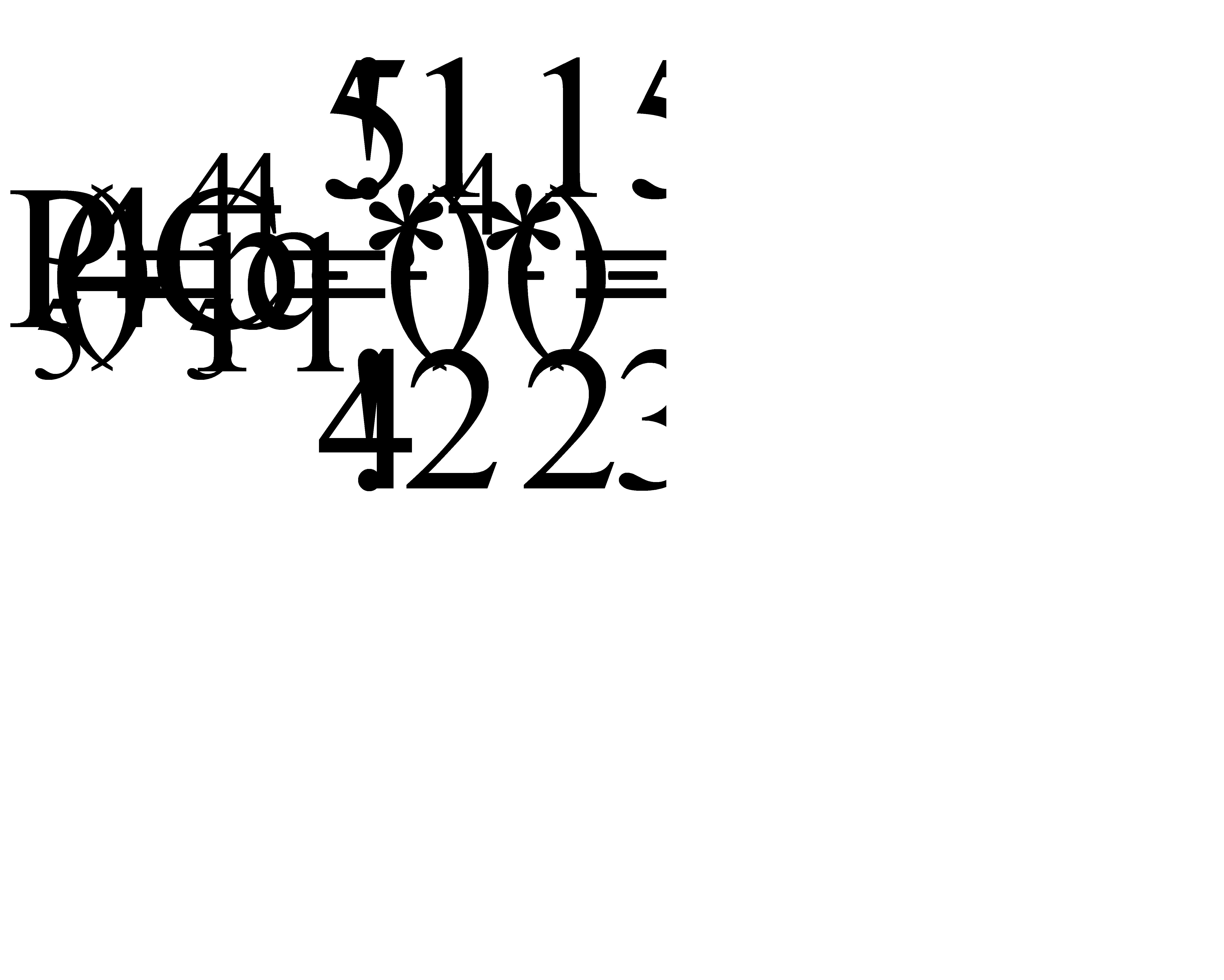 ,
, 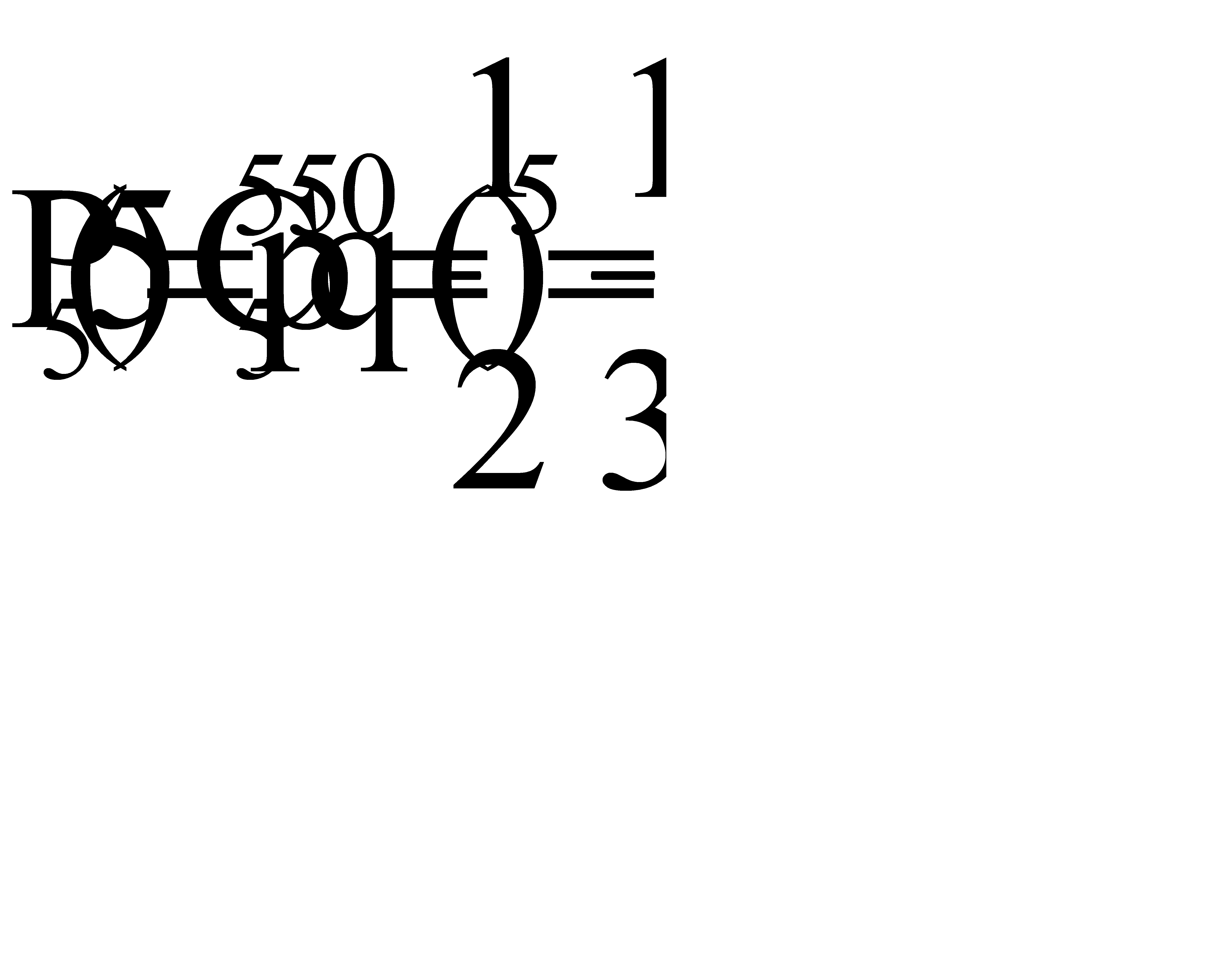 ,
, 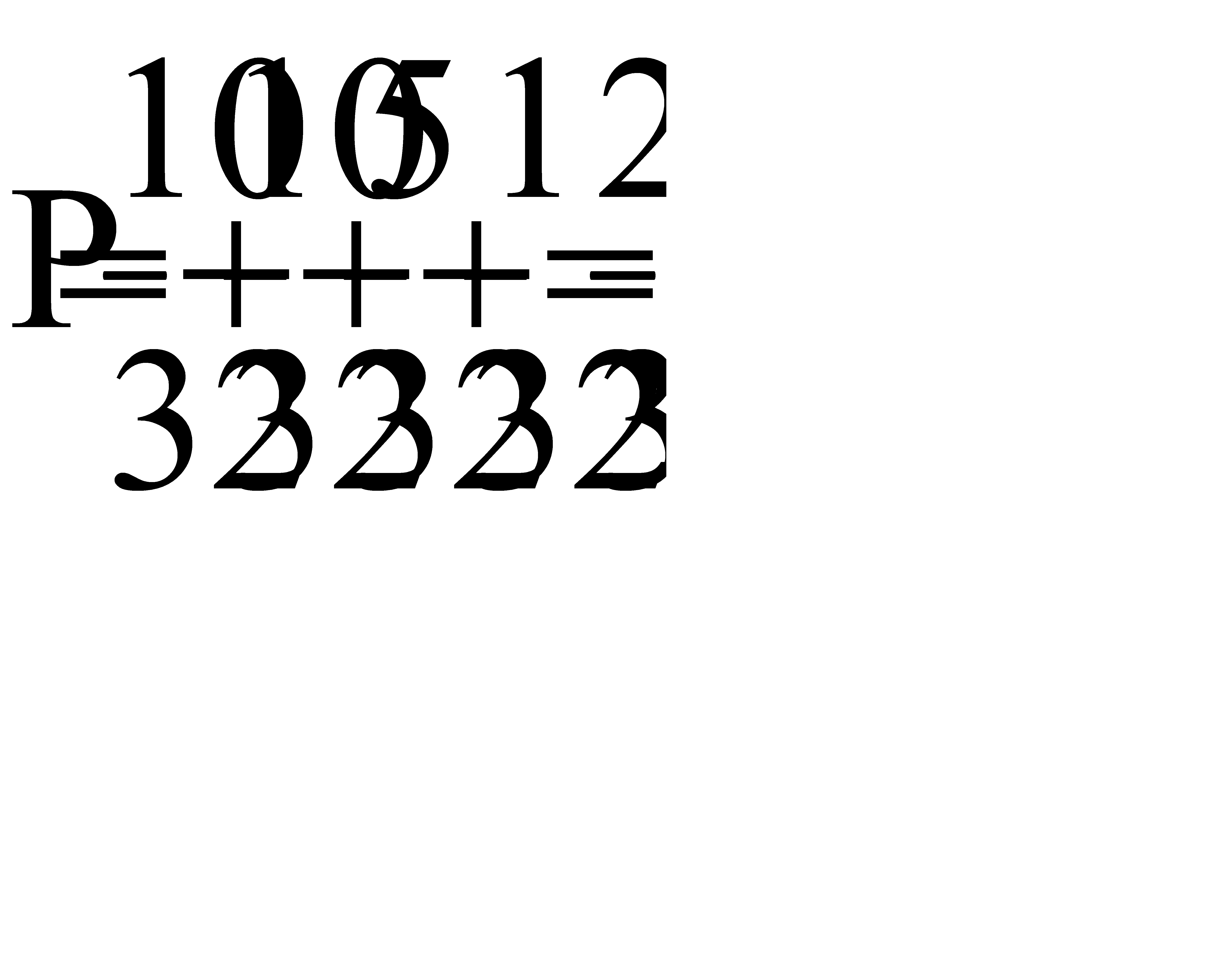
Ответ: a) 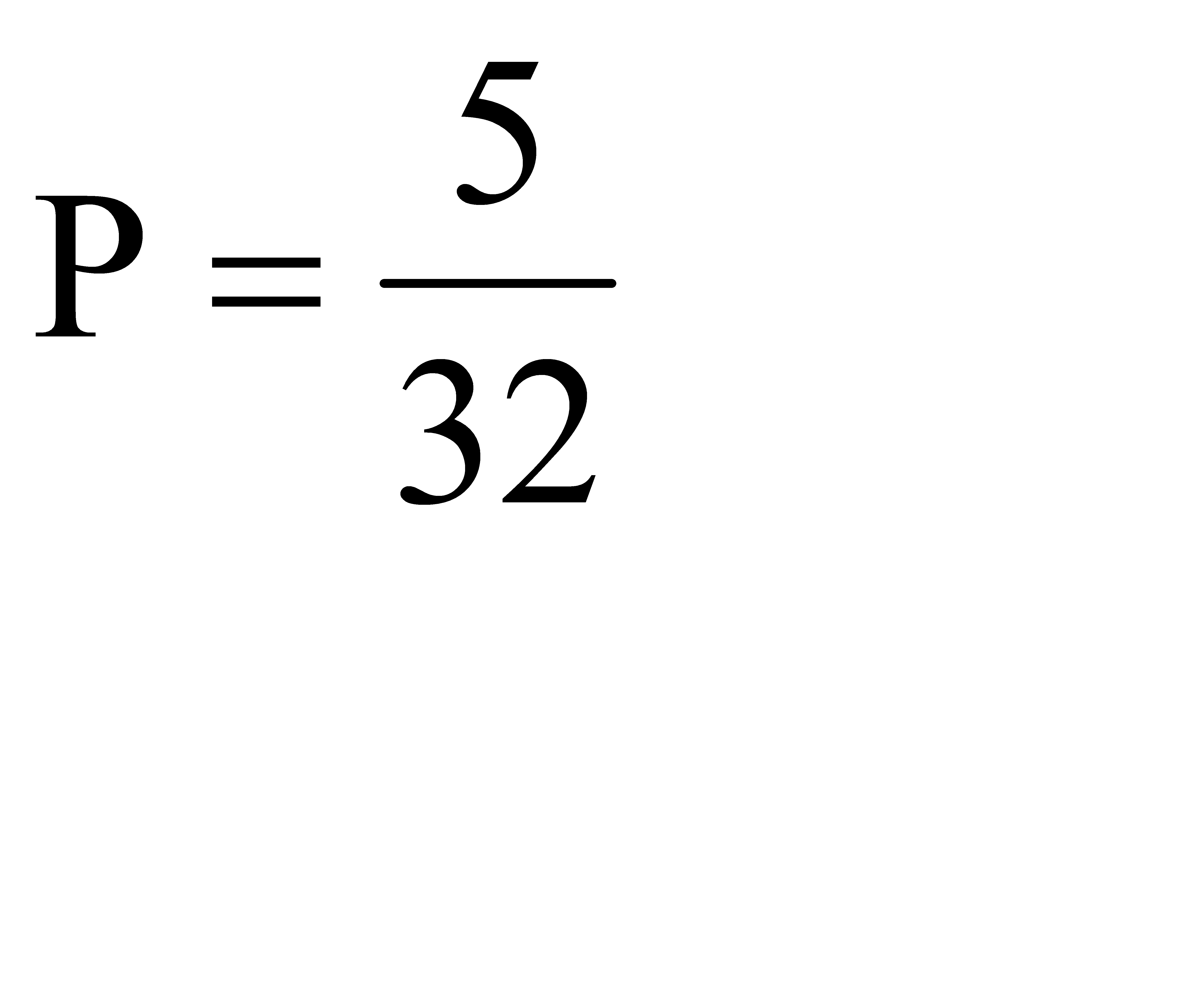 ; б)
; б) 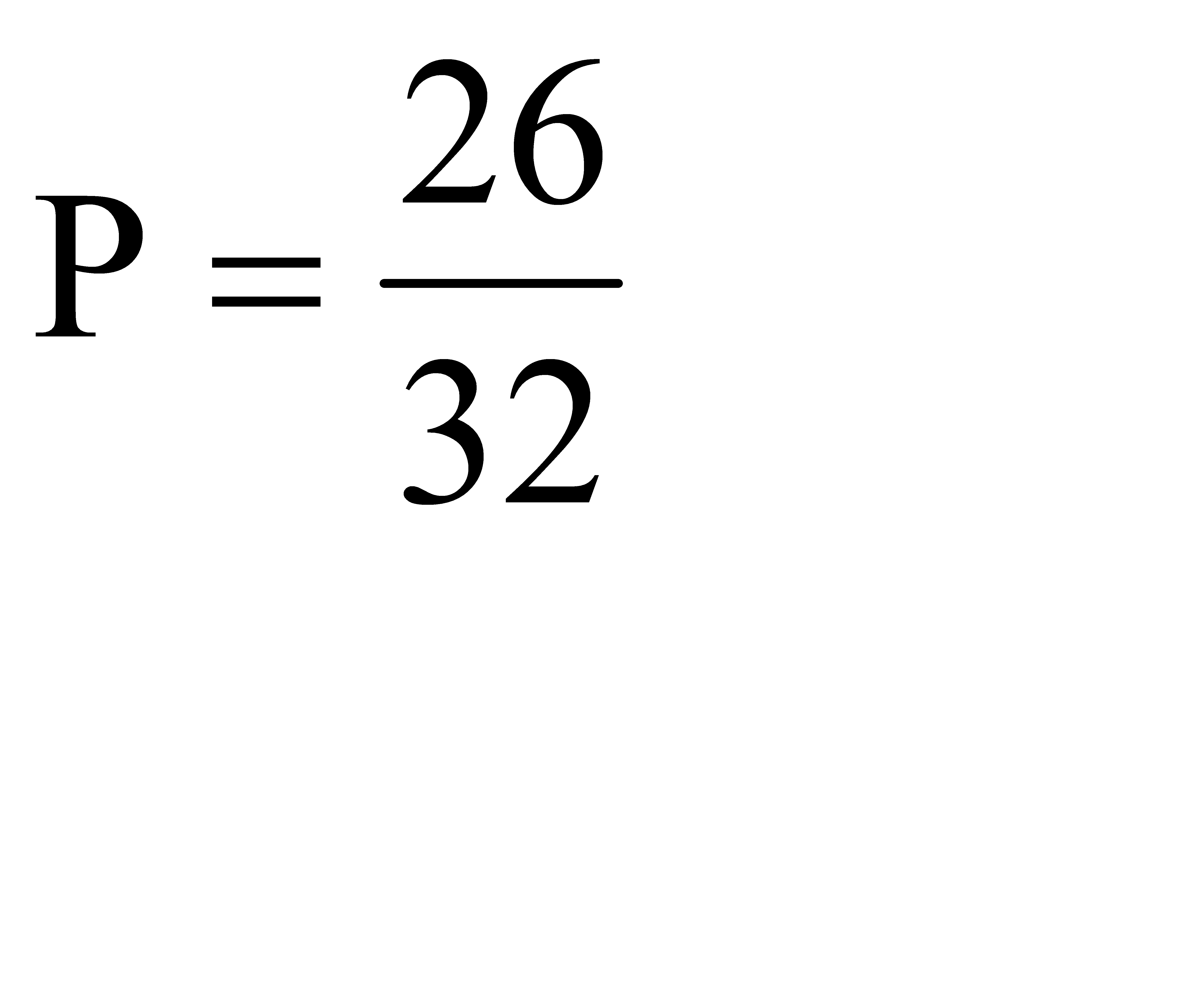
#113а)Так как вероятность появления события А во всех испытаниях одинакова и все испытания независимы, то применяем формулу Бернулли. Так как вероятность появления события А в одном испытании равна 0, 4, т. е. р = 0, 4, то вероятность не появления события А в одном испытании равна q = 1- 0, 4 = 0, 6.
Найдём вероятность того, что событие А появится ровно 3 раза в четырёх независимых испытаниях и найдём вероятность того, что событие А появится ровно 4 раза в четырёх независимых испытаниях и просуммируем их: 
б) Так как вероятность появления события А во всех испытаниях одинакова и все испытания независимы, то применяем формулу Бернулли. р = 0, 8 q = 0, 2Найдём вероятности того, что событие А появится ровно 4 раза и 5 раз в пяти нез-хисы-х и просумм: 
Ответ: а) 0, 1792, б) 0, 73728
#114 По условию 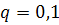 , следовательно вероятность стабильной работы каждого элемента
, следовательно вероятность стабильной работы каждого элемента 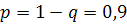 . Так как безразлично какой из элементов откажет и вероятности отказа всех элементов равны, применима формула Бернулли. а) Найдём вероятность того, что будут работать все 3 элемента
. Так как безразлично какой из элементов откажет и вероятности отказа всех элементов равны, применима формула Бернулли. а) Найдём вероятность того, что будут работать все 3 элемента 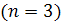 :
: 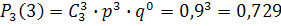 б) Найдём вероятность того, что устройство будет работать при одном дополнительном элементе на протяжении времени t.
б) Найдём вероятность того, что устройство будет работать при одном дополнительном элементе на протяжении времени t. 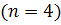 :
: 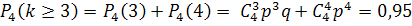
в) Найдём вероятность того, что устройство будет работать при двух дополнительных элементах на протяжении времени t. 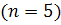 :
: 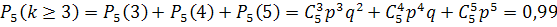
#115 По условию 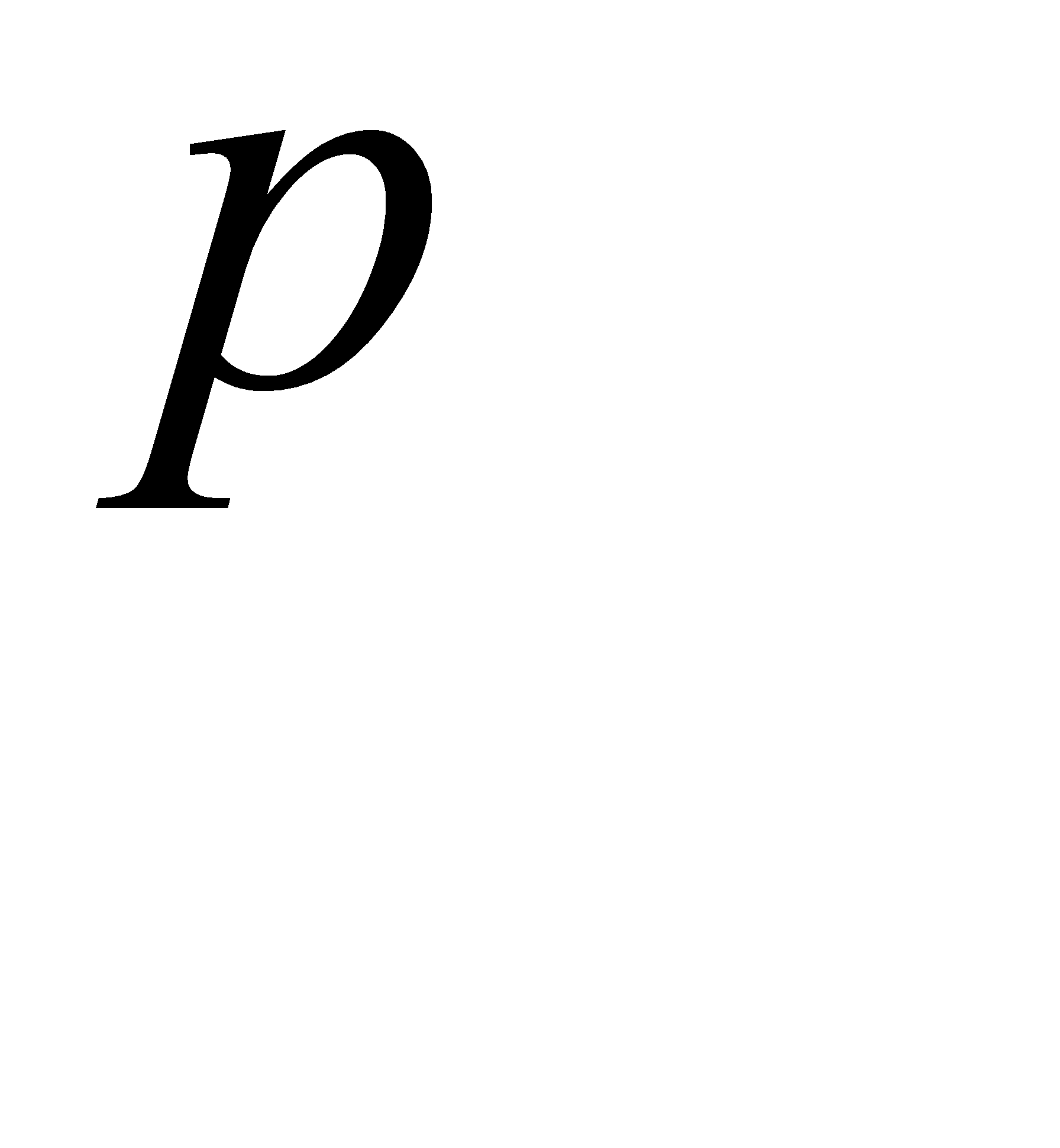 =0. 51 следовательно вероятность
=0. 51 следовательно вероятность 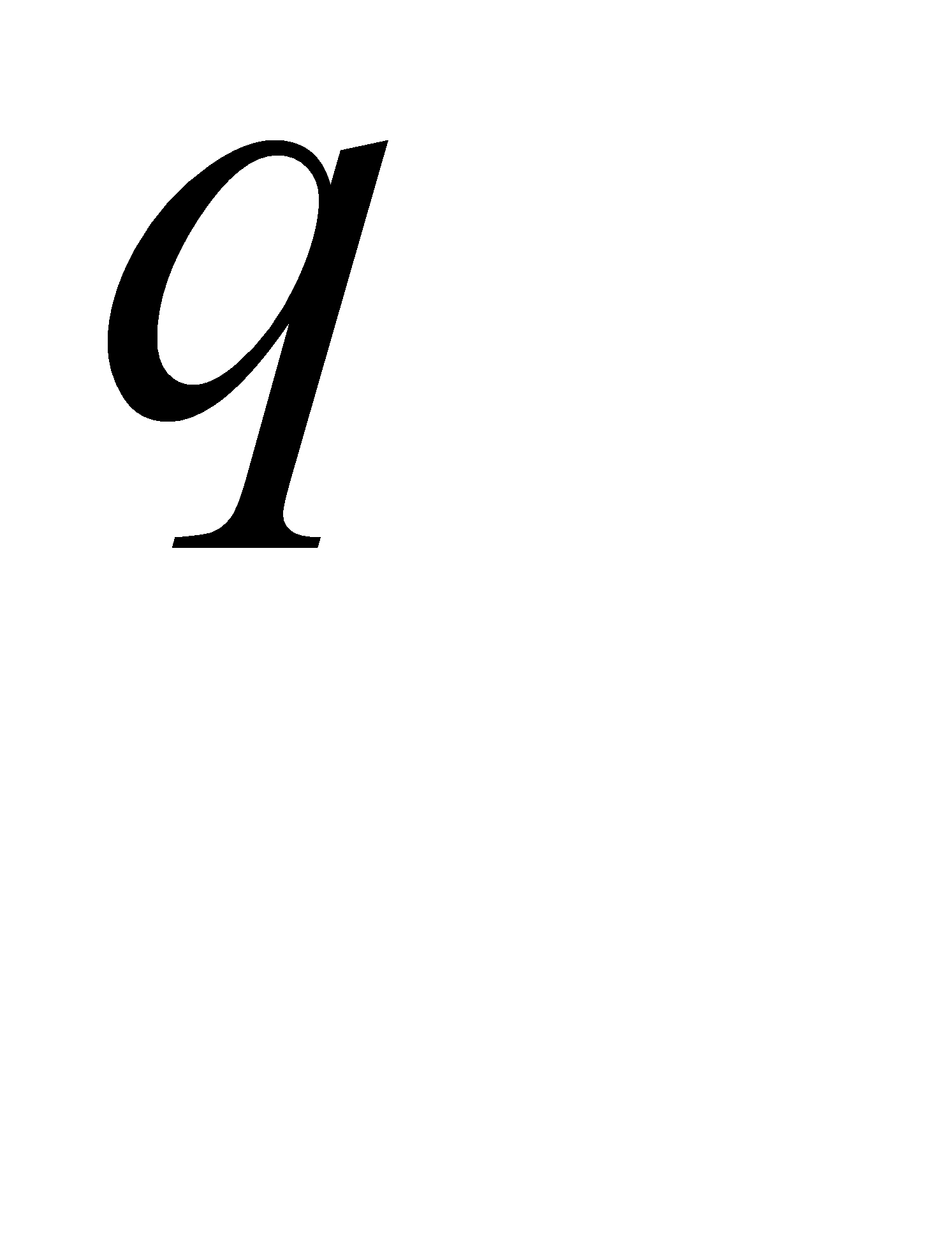 = 0. 49 и применима формула Бернулли.
= 0. 49 и применима формула Бернулли.
а) Найдём вероятность того, что в семье 2 мальчика:  0. 62
0. 62
б) Найдём вероятность того, что в семье не более двух мальчиков: 
в) Найдём вероятность того, что в семье более двух мальчиков:

г) найдём вероятность того, что в семье не менее двух и не более трёх мальчиков: 
#117Решение: т. к. p = xa - вероятность того, что точка будет находиться на расстоянии меньшем чем x, следовательно, q = 1 – p=1- xa= a-xa. По формуле Бернулли имеем: Pnk= Cnkpkqn-k. P52= C52xa2a-xa3.
#118Решение: вероятность того, что точка попадет в нужный отрезок равна р=1/4. q=3/4 искомая вероятность равна Р= С82 С62 С42 С22*(1/4)8.
#119 По условию, n=243; k=70; p=0, 25; q=0, 75. Т. к. n=243 – достаточно большое число, воспользуемся локальной теоремой Лапласа: 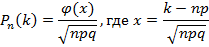
Найдем значение x: 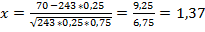 . По таблице найдем
. По таблице найдем 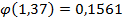
Тогда искомая вероятность 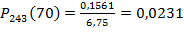 Ответ:
Ответ: 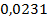 .
.
#120 По условию, n=2400; k=1400; p=0, 6; q=0, 4. Так как n=2400 – достаточно большое число, воспользуемся локальной теоремой Лапласа: 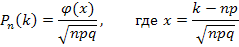 . Найдем значение x:
. Найдем значение x: 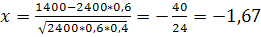 .
.
Так как 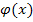 четная функция, то
четная функция, то 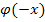 =
= 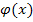 . По таблице найдем
. По таблице найдем 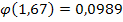
Тогда искомая вероятность 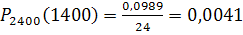 Ответ: 0, 0041.
Ответ: 0, 0041.
#121Так как n велико, воспользуемся локальной теоремой Лапласа: 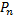 (k)=
(k)= 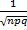 φ (x).
φ (x).
Вычислим x: X= 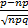 =
= 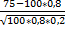 =-1, 25. Функция φ (x) четная, поэтому φ (-1, 25)= φ (1, 25)=0, 1826.
=-1, 25. Функция φ (x) четная, поэтому φ (-1, 25)= φ (1, 25)=0, 1826.
Искомая вероятность 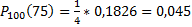 .
.
#122P(k)= 1/√ (npq)*Вычислим х: х_р—пр_ 1400—24000, 6 _ 40, Vnpq ~ У 2400 -0, 6 0, 4 " ~ 24 ~ Функция ф(^)=—^=е~лг*/'2—четная, поэтому ф(—1, 67)=ф( 1, 67). По таблице приложения 1 найдем ф( 1, 67) = 0, 0989.
Искомая вероятность Я24оо A400) = 1/24-0, 0989=0, 0041.
#123n=2N, k=N, p=0, 5, q=0, 5. Для нахождения вероятности выпадения «герба» ровно N раз воспользуемся локальной теоремой Лапласа: 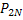 (N)=φ (x)* 1/
(N)=φ (x)* 1/ 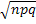 ; φ (x)=
; φ (x)= 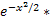 1/
1/ 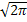 ; x=(k-pn)/
; x=(k-pn)/ 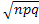 ; x=0; φ (x)≈ 0, 3989;
; x=0; φ (x)≈ 0, 3989; 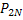 N)≈ 0. 5641/
N)≈ 0. 5641/ 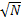 Монета брошена 2N раз. Найти вероятность того, что «герб» выпадет на 2m раз больше, чем
Монета брошена 2N раз. Найти вероятность того, что «герб» выпадет на 2m раз больше, чем
#124Т. к. исход каждого испытания не зависит от предыдущих исходов и возможных исходов два («герб» или надпись), то вероятность выпадения «герба» в каждом испытании равна 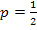 . Всего проведено n=2N испытаний, а «герб» выпал на 2m раза больше, чем надпись, значит обозначим количество выпадений «герба» за t, получим уравнение:
. Всего проведено n=2N испытаний, а «герб» выпал на 2m раза больше, чем надпись, значит обозначим количество выпадений «герба» за t, получим уравнение: 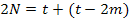 . Очевидно, что количество исходов, в которых выпал «герб», равно
. Очевидно, что количество исходов, в которых выпал «герб», равно 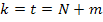 .
.
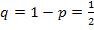 По локальной теореме Лапласа вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p, событие наступит ровно k раз, равна:
По локальной теореме Лапласа вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p, событие наступит ровно k раз, равна: 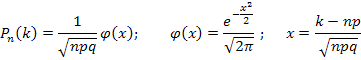
Подставим значения: 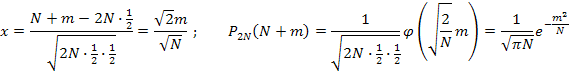
#125 воспользуемся интегральной теоремой Лапласа: 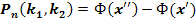 , где
, где 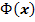 – функция Лапласа,
– функция Лапласа, 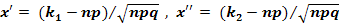 a) По условию,
a) По условию, 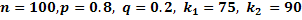 . Вычислим
. Вычислим 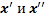 :
:
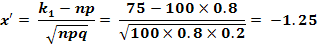
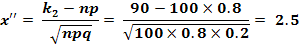
Учитывая, что функция Лапласа нечетна, т. е. 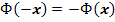 , получим:
, получим:
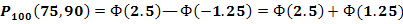 .
.
По таблице приложения 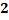 найдем:
найдем:
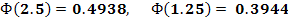 .
.
Искомая вероятность:
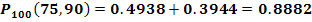
б) Требование, чтобы событие появилось не менее 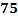 раз, означает, что число появления событий может быть равно
раз, означает, что число появления событий может быть равно 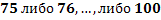 . Таким образом в рассматриваемом случае следует принять
. Таким образом в рассматриваемом случае следует принять 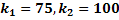 . Тогда:
. Тогда:
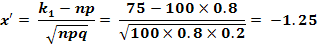
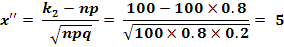
По таблице приложения 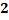 найдем:
найдем:
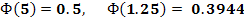 .
.
Искомая вероятность:
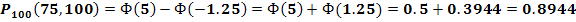
в) События – « 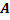 появилось не менее
появилось не менее 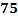 раз» и «
раз» и « 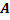 появилось не более
появилось не более 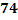 раз» противоположны, поэтому сумма вероятностей этих событий равна единице. Следовательно, искомая вероятность:
раз» противоположны, поэтому сумма вероятностей этих событий равна единице. Следовательно, искомая вероятность:
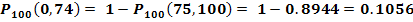
#126Вероятность появления события в каждом из 2100 испытаний равна 0, 7. Найти вероятность того что событие появится не менее 1470 и не более 1500 раз. Решение: Воспользуемся интегральной теоремой Лапласа: 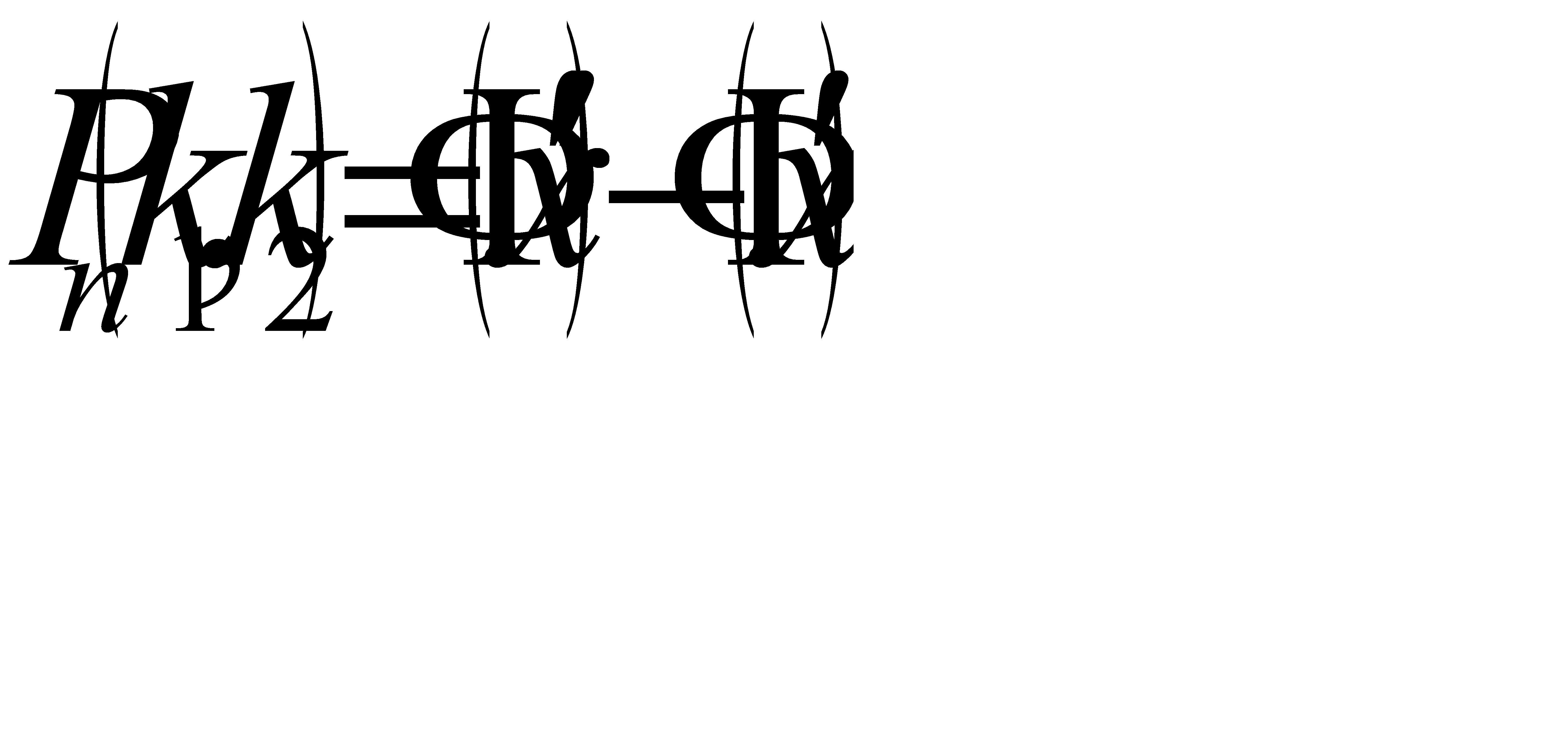 , где Ф(х)- функция Лапласа,
, где Ф(х)- функция Лапласа, 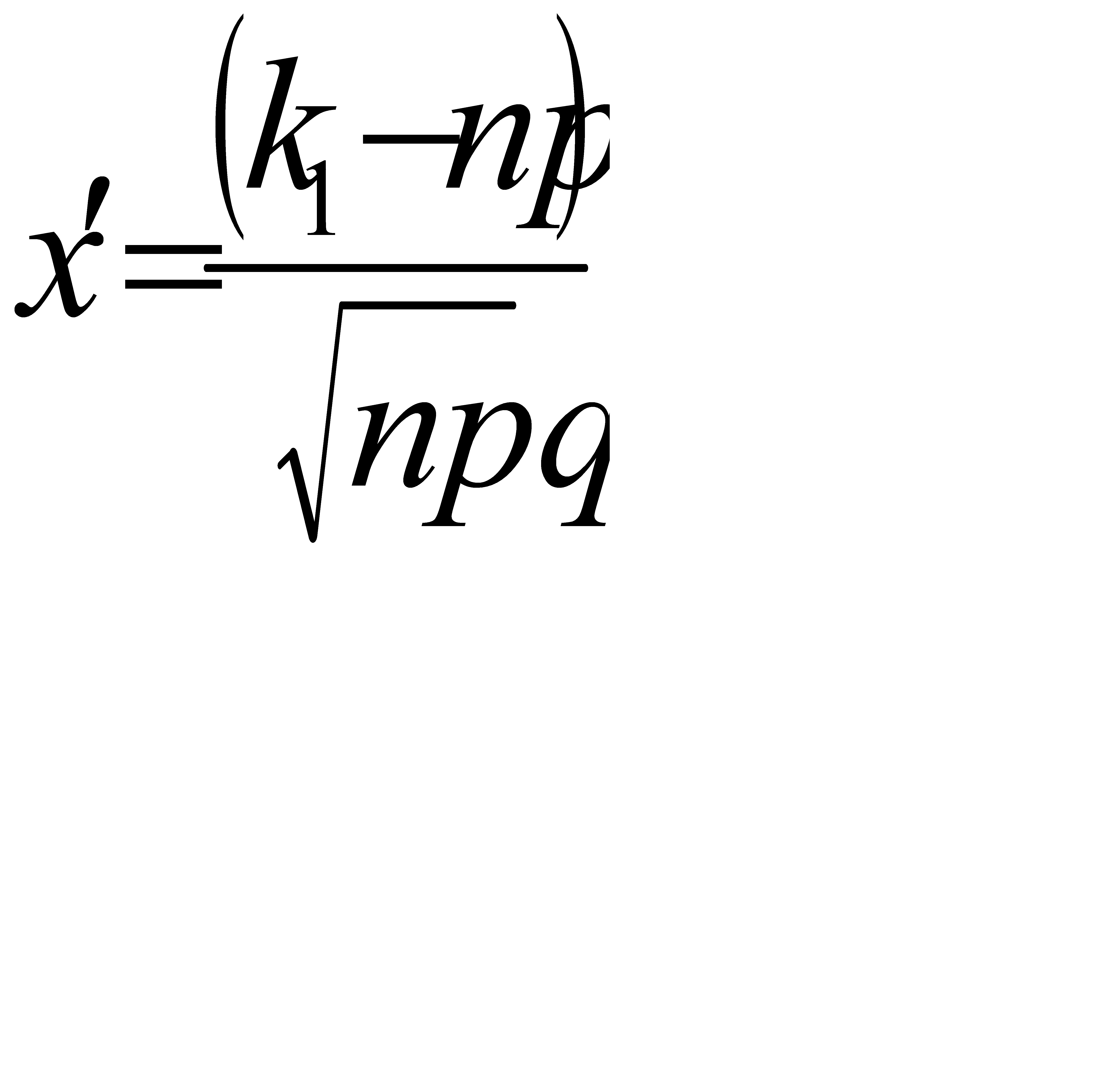 ,
, 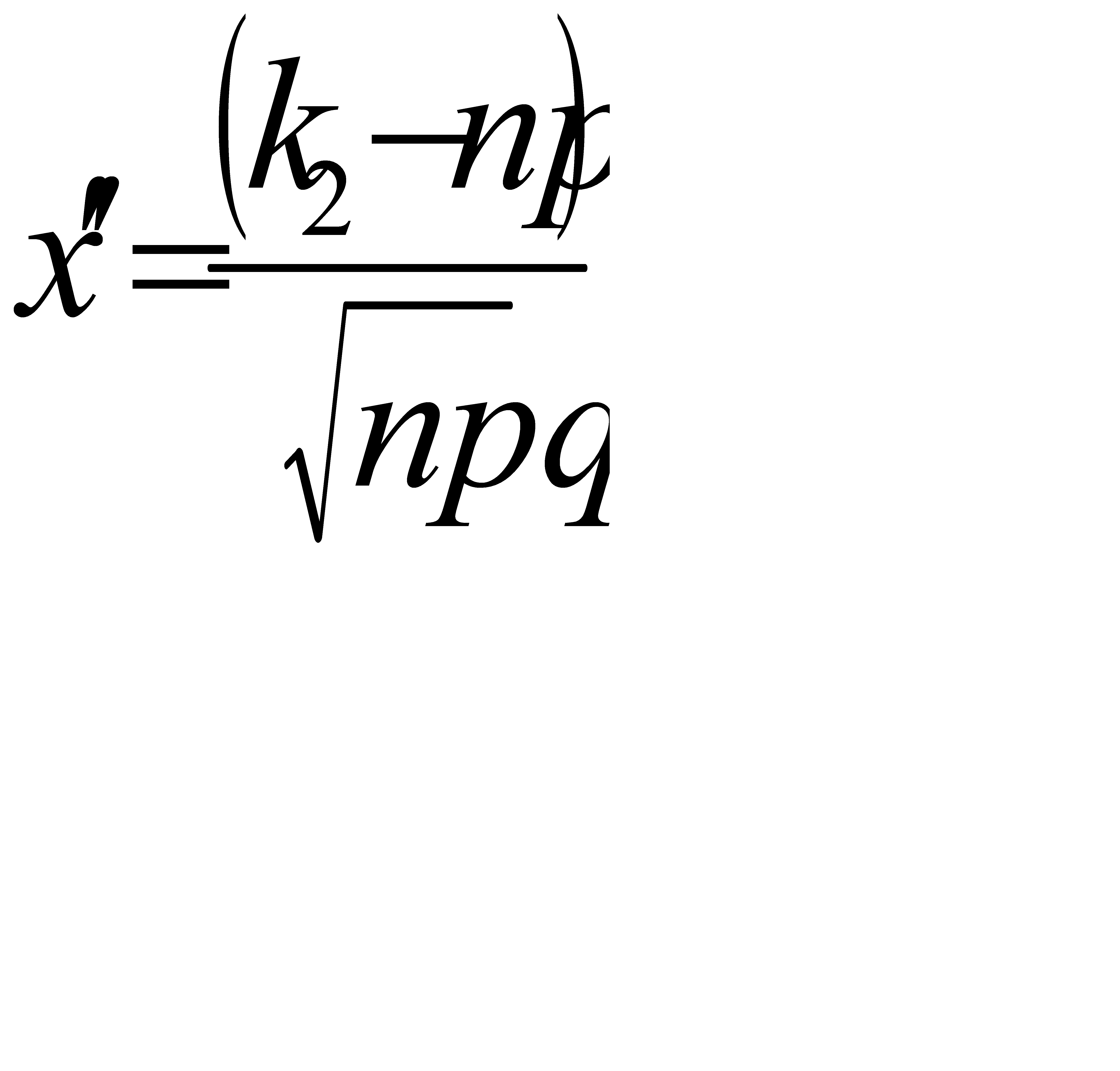
По условию, n= 2100; p=0, 7; q=0, 3; k1= 1470; k2= 1500; Тогда 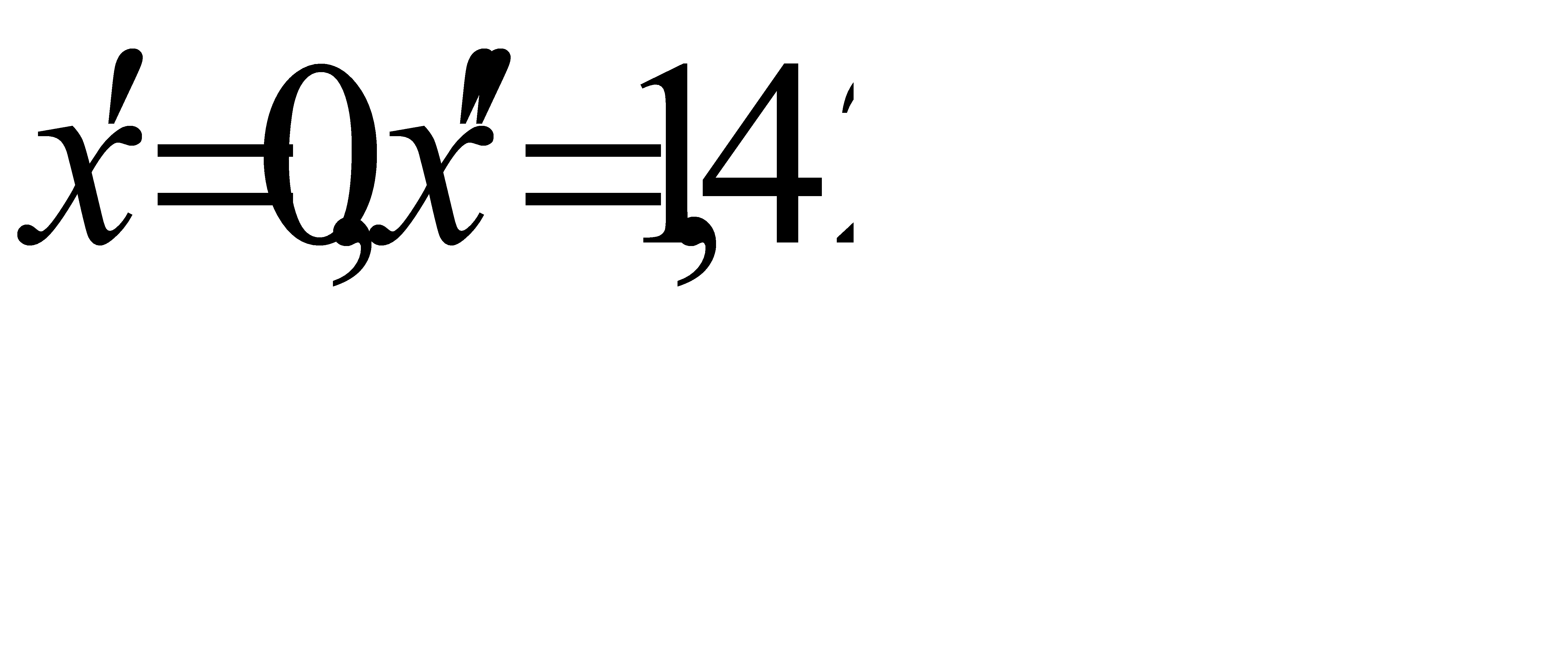 ; По таблице значений функции Лапласа:
; По таблице значений функции Лапласа:
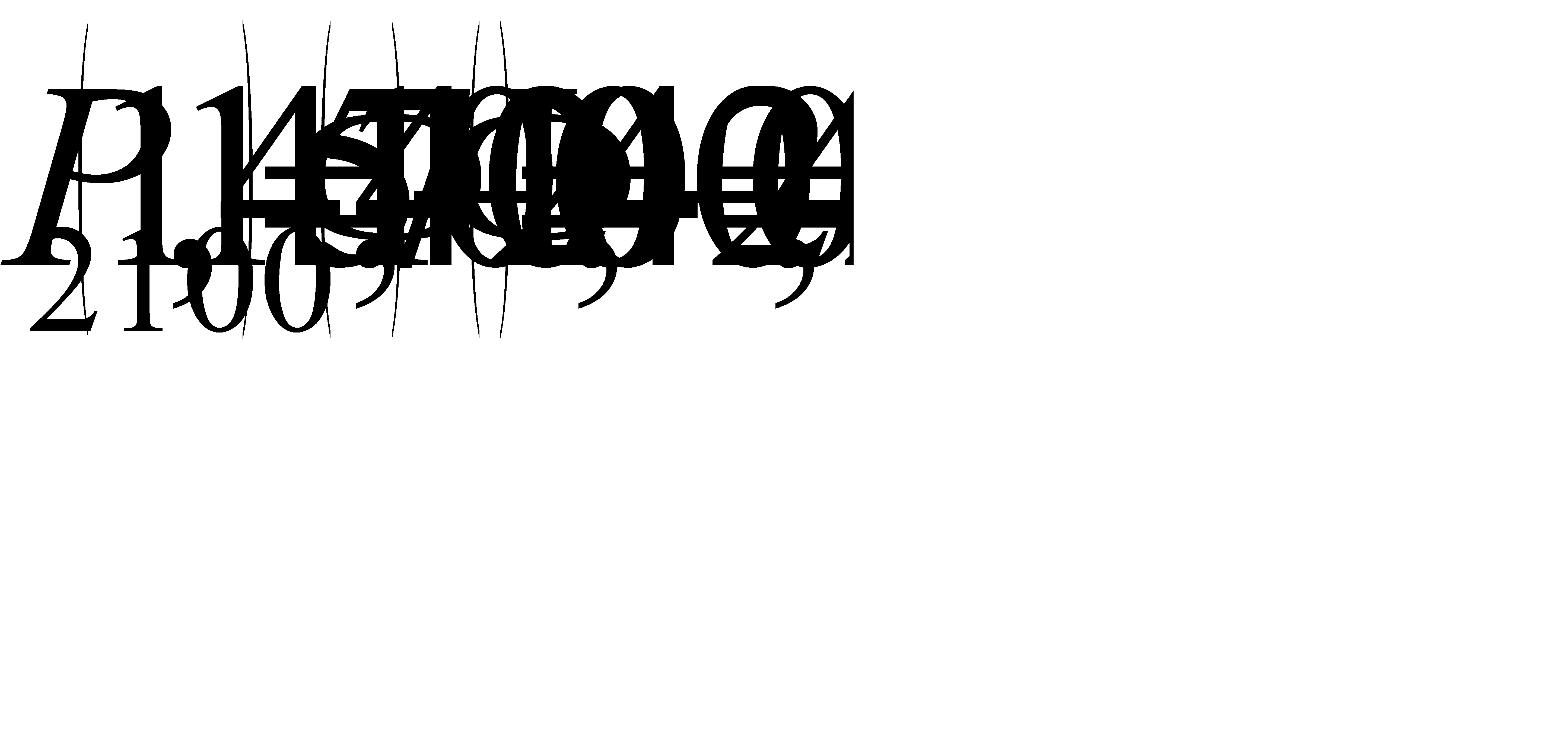
#127 воспользуемся интегральной теоремой Лапласа: 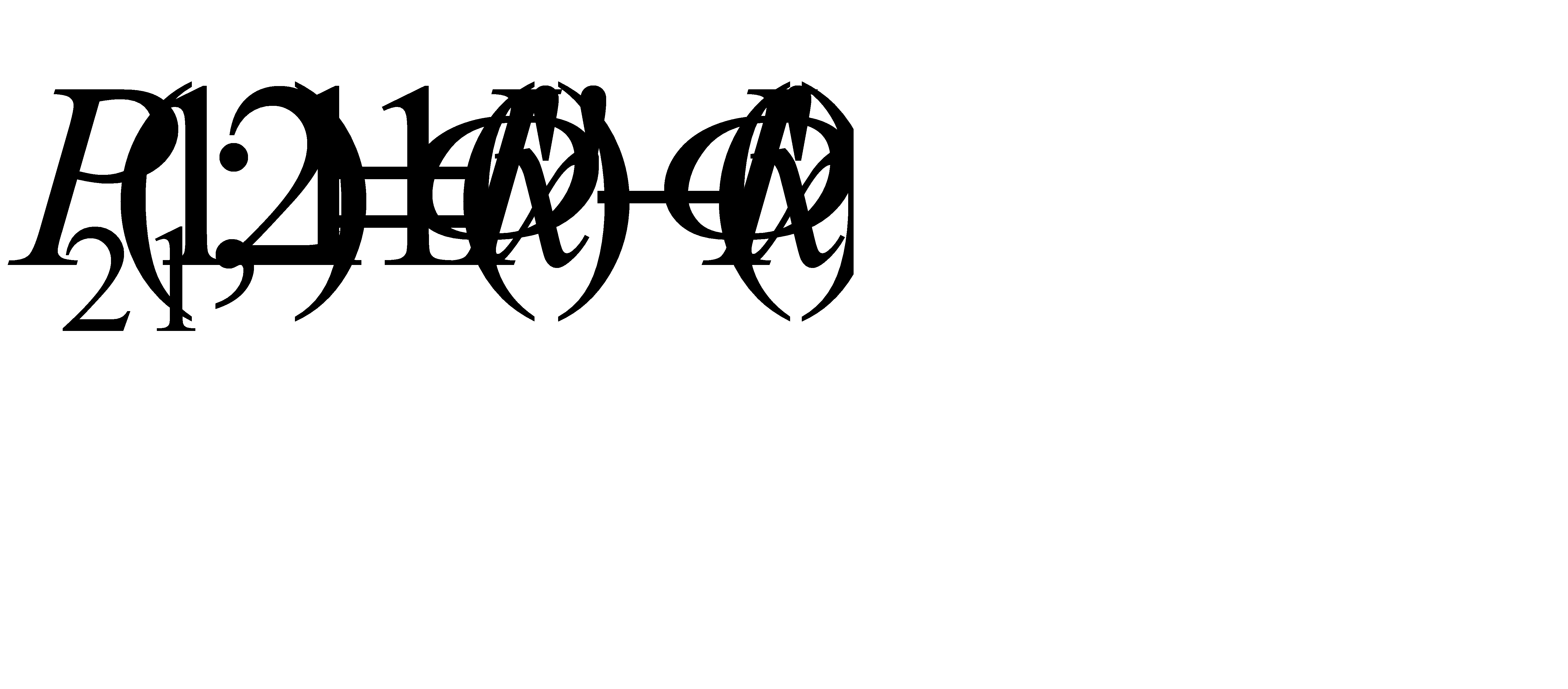 где
где 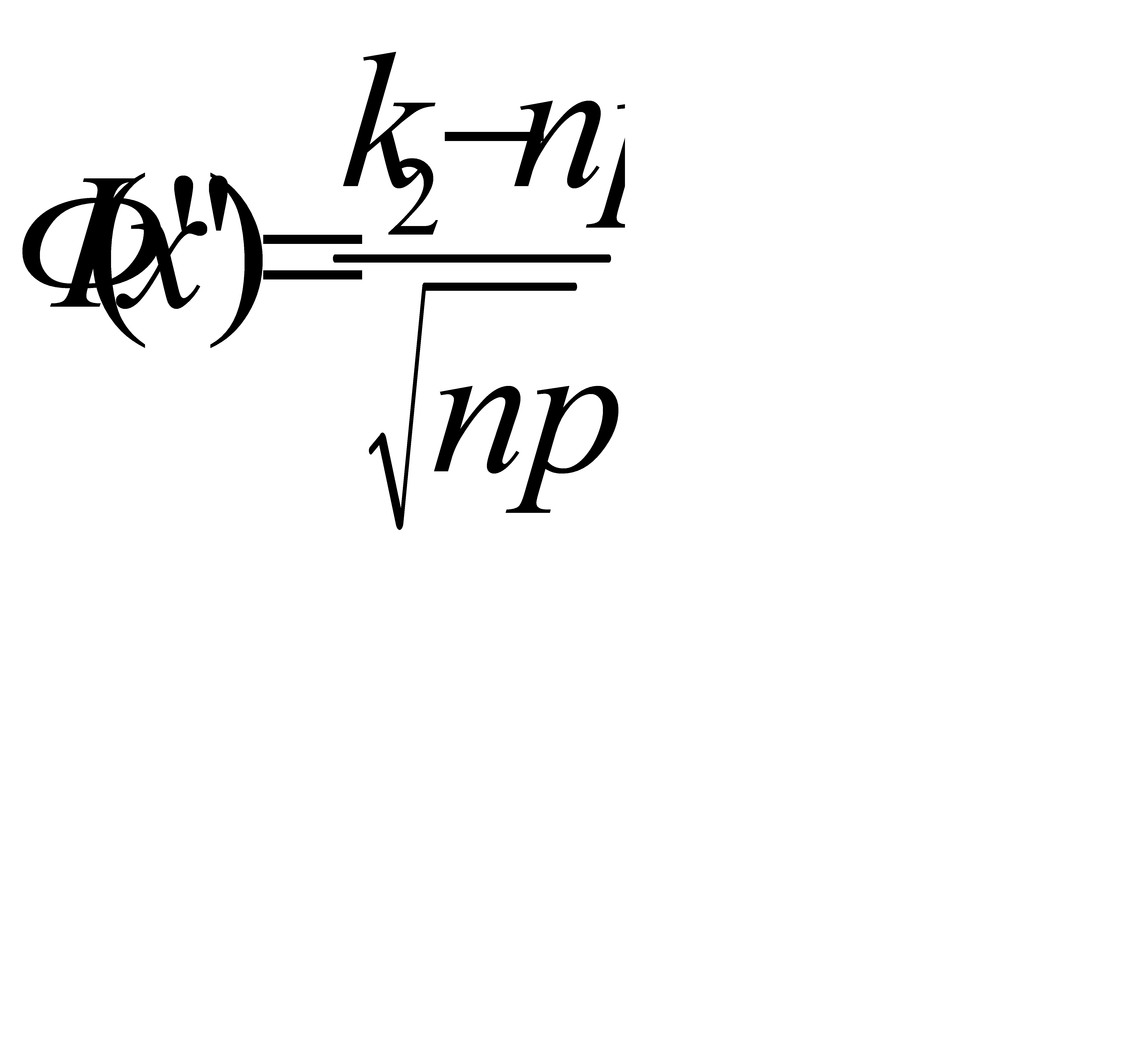 и
и 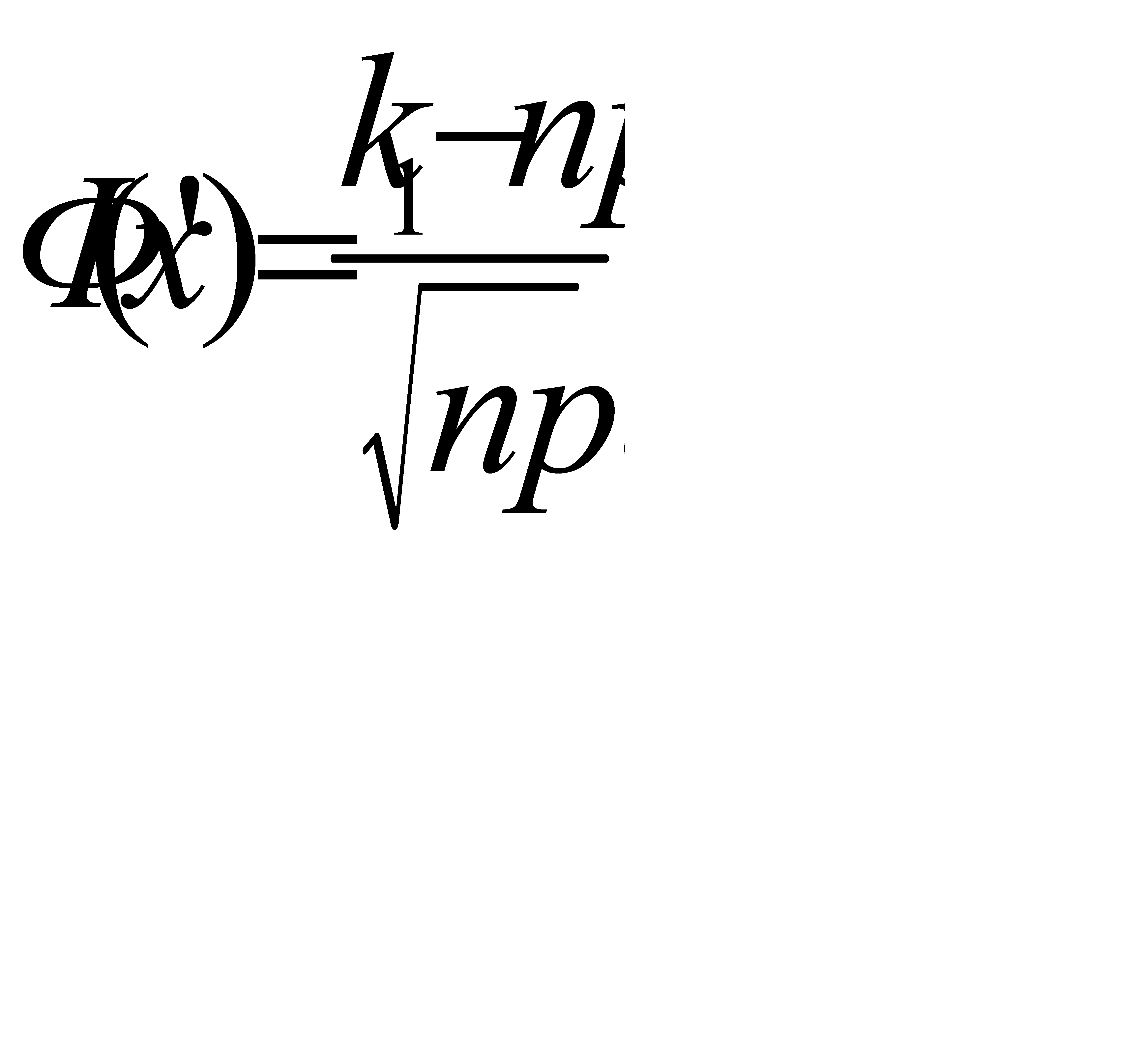 ,
, 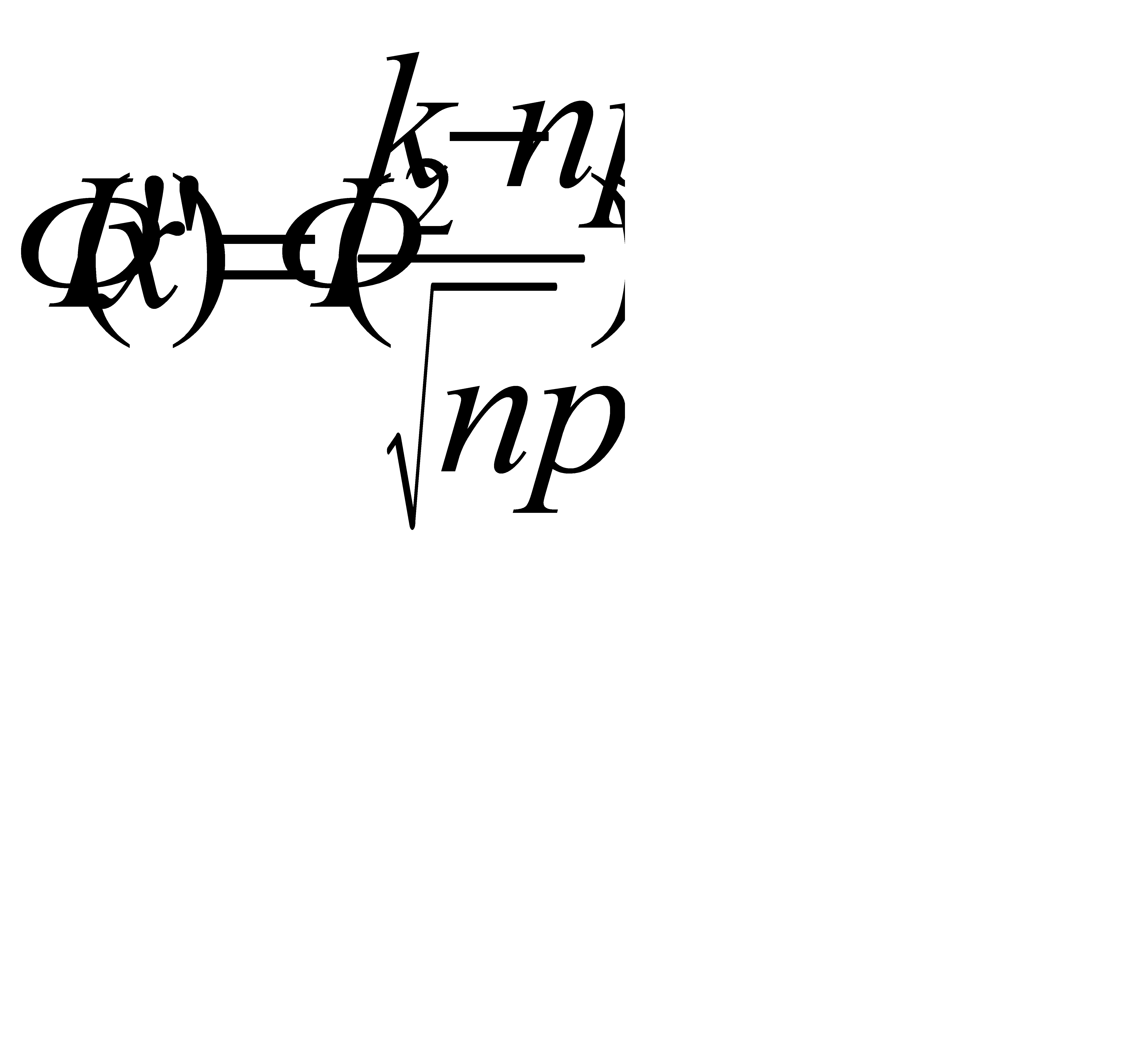 =
=  (21-14, 3/2, 1)=
(21-14, 3/2, 1)=  (3)=0, 4986;,
(3)=0, 4986;, 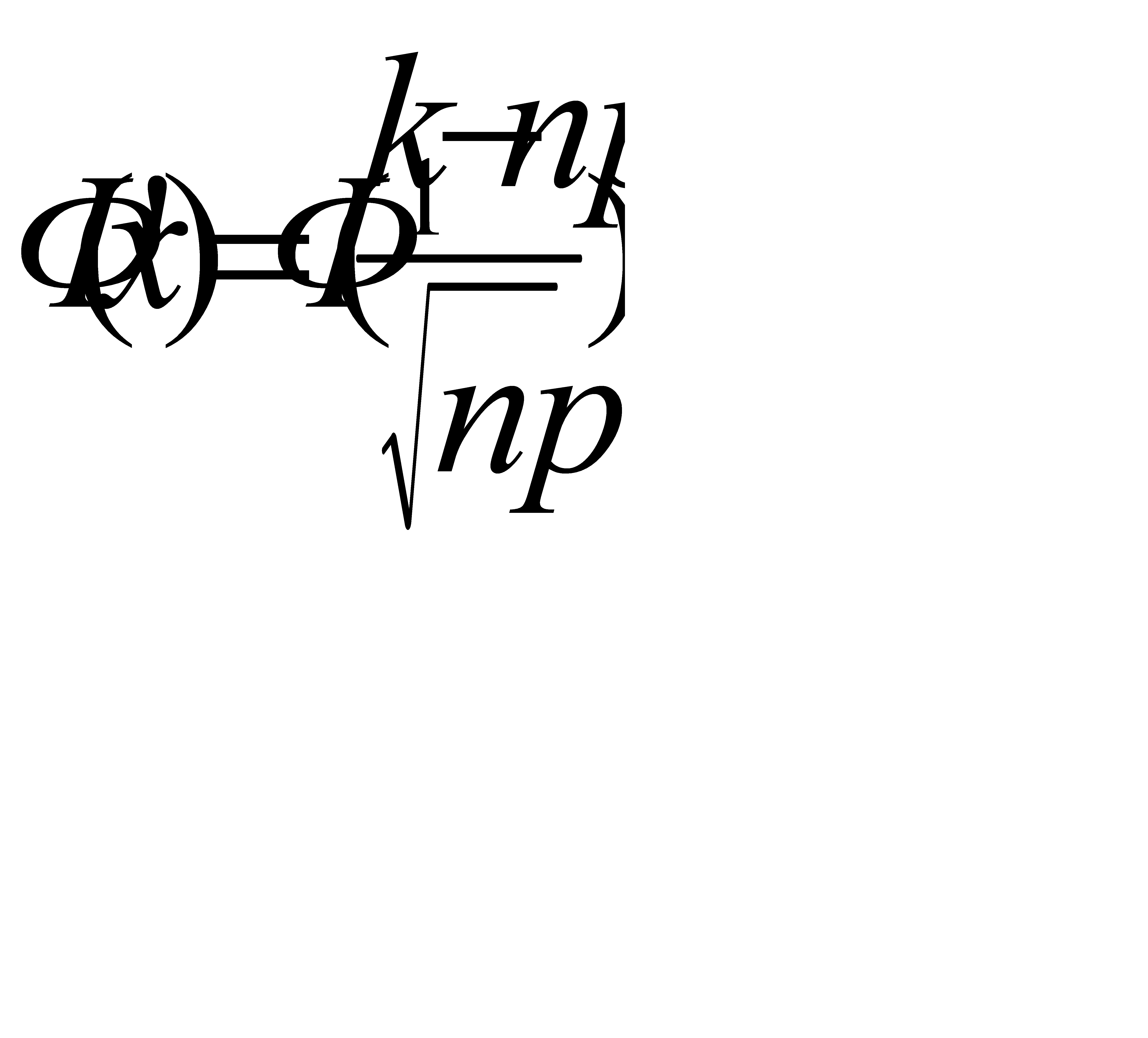 =
=  (11-14, 3/2, 1)=
(11-14, 3/2, 1)=  (-1, 7)=0, 4532Так как функция Лапласа нечетная то получим следующее равенство:
(-1, 7)=0, 4532Так как функция Лапласа нечетная то получим следующее равенство: 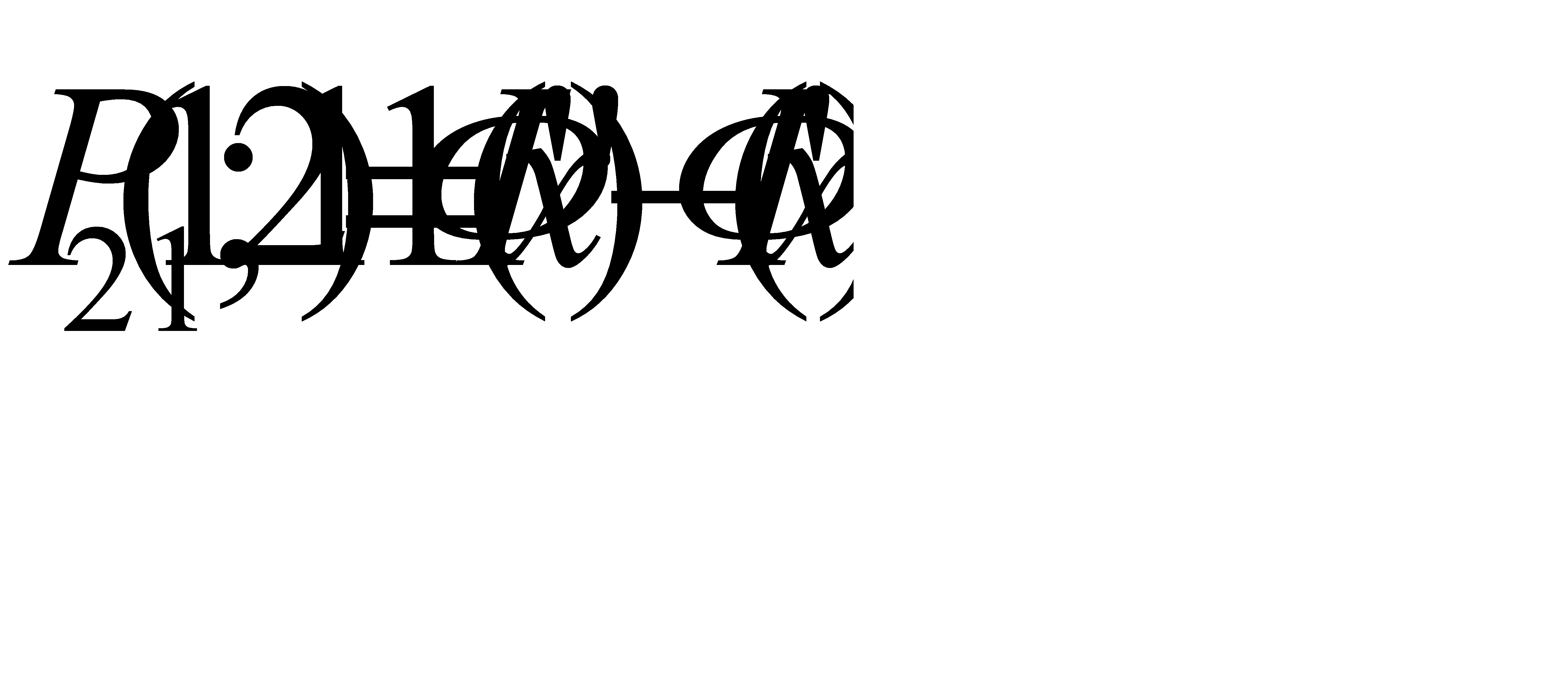 =
= 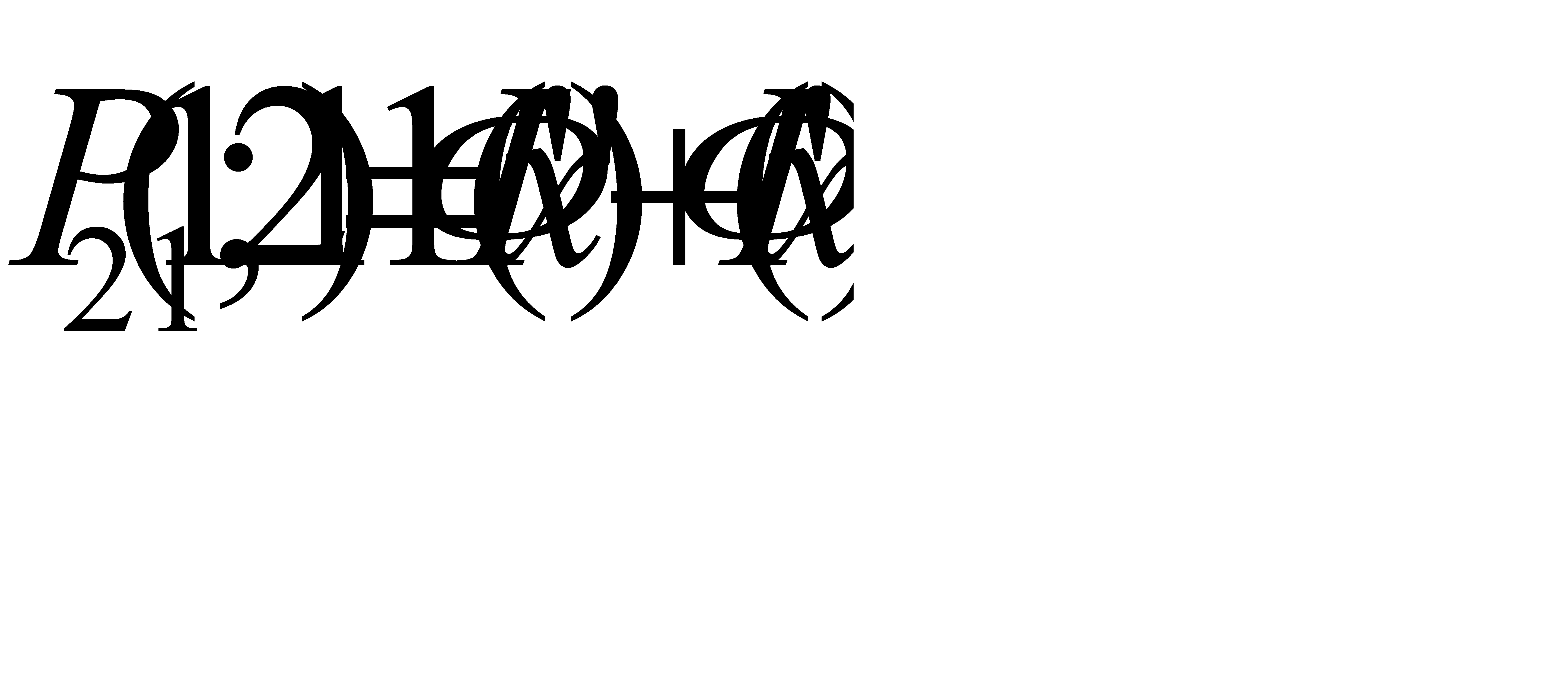 =0, 4986+0, 4532=0, 9518Ответ: 0, 9518
=0, 4986+0, 4532=0, 9518Ответ: 0, 9518
#128Воспользуемся интегральной теоремой Лапласа: 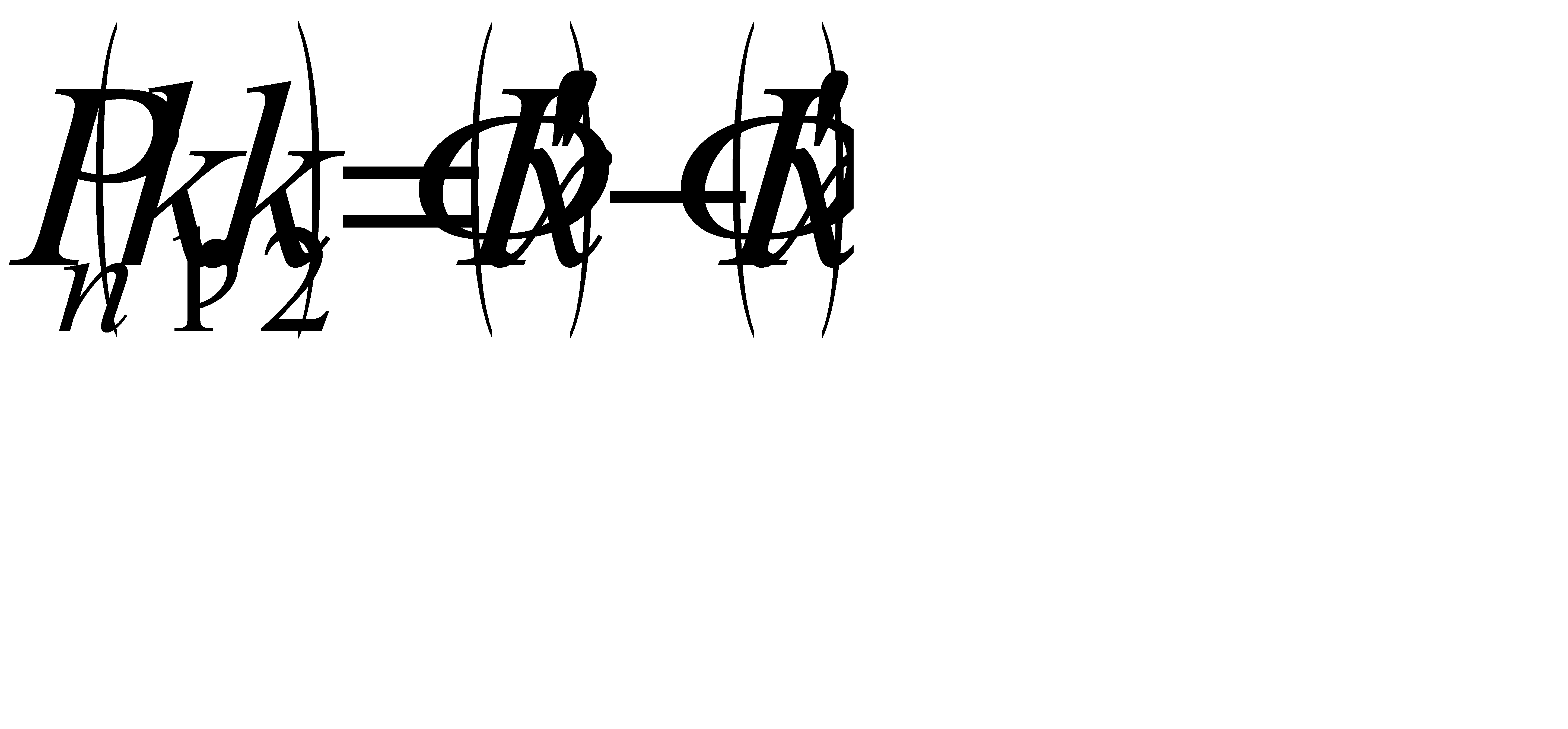 , где Ф(х) – функция Лапласа,
, где Ф(х) – функция Лапласа,
 ,
, 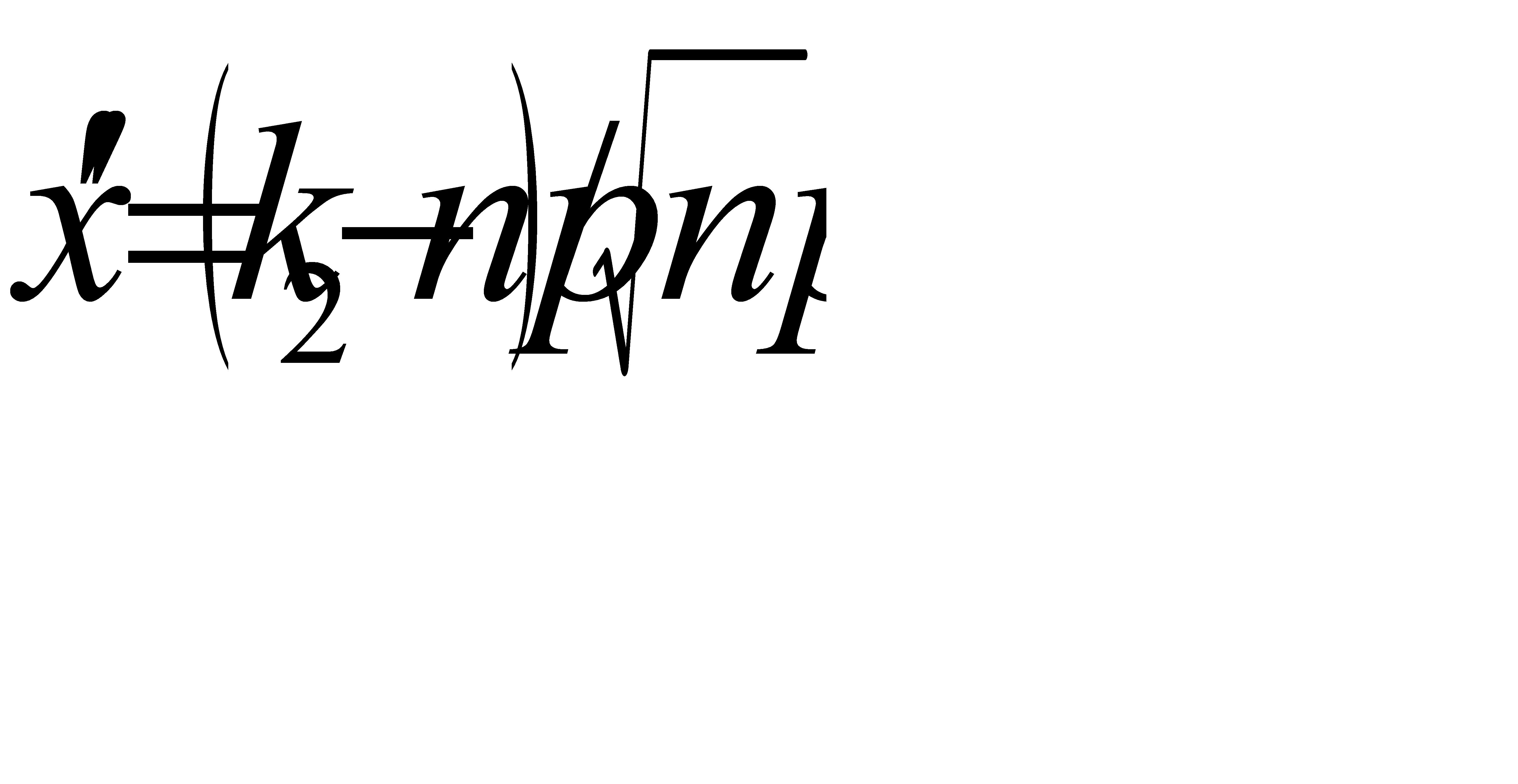 , По условию задачи n=N; p=0, 5; q=0, 5,
, По условию задачи n=N; p=0, 5; q=0, 5, 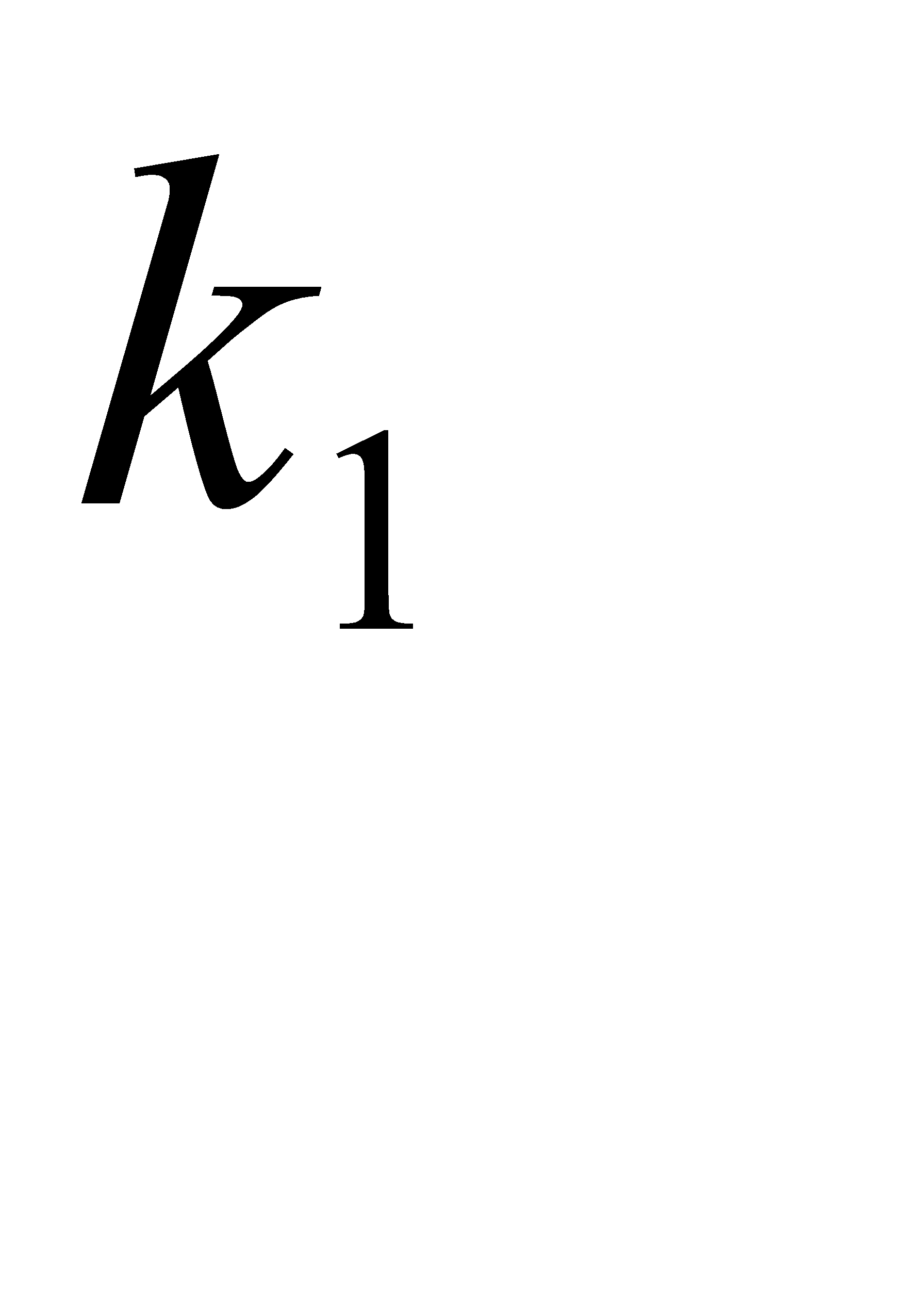 =
= 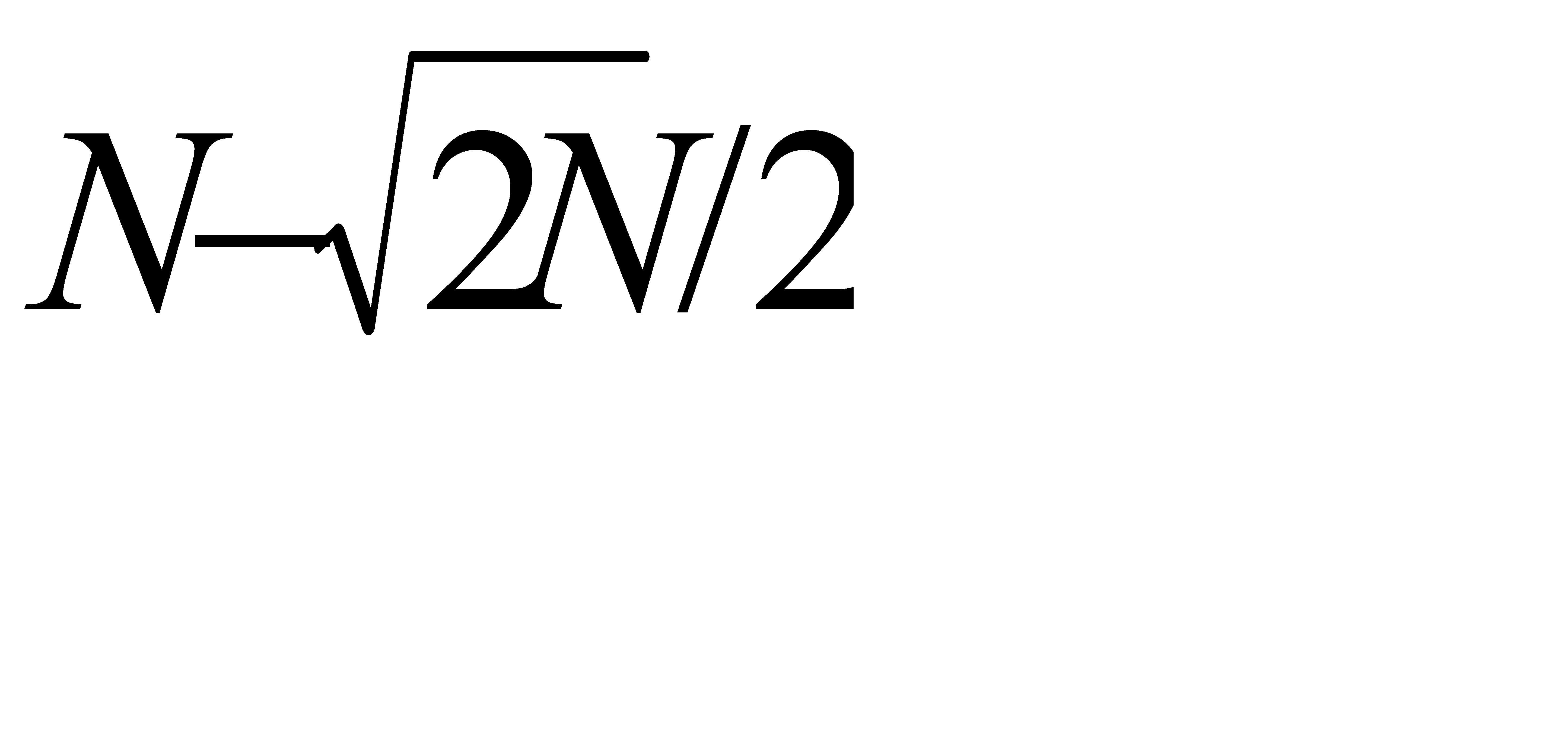 ;
; 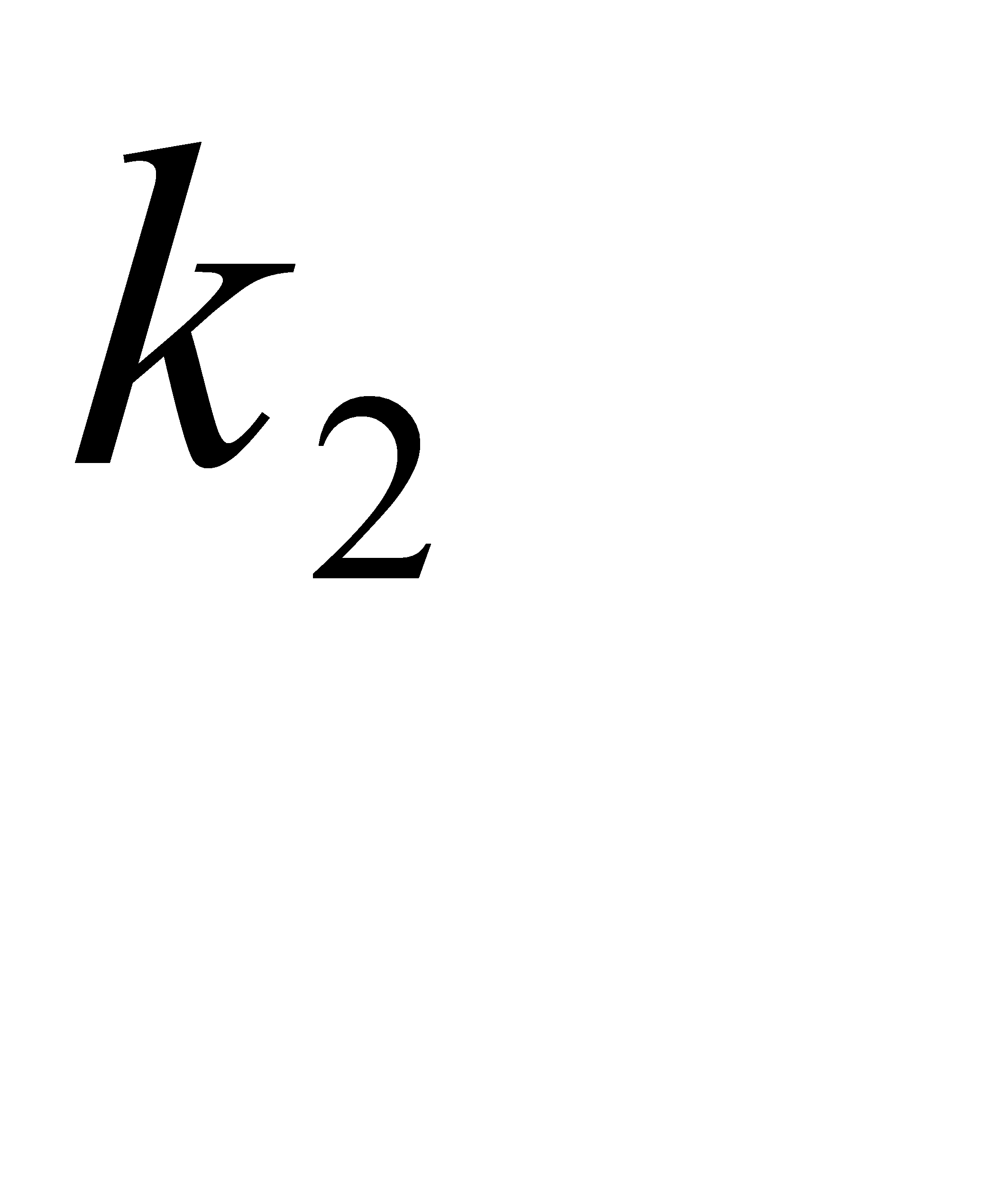 =
= 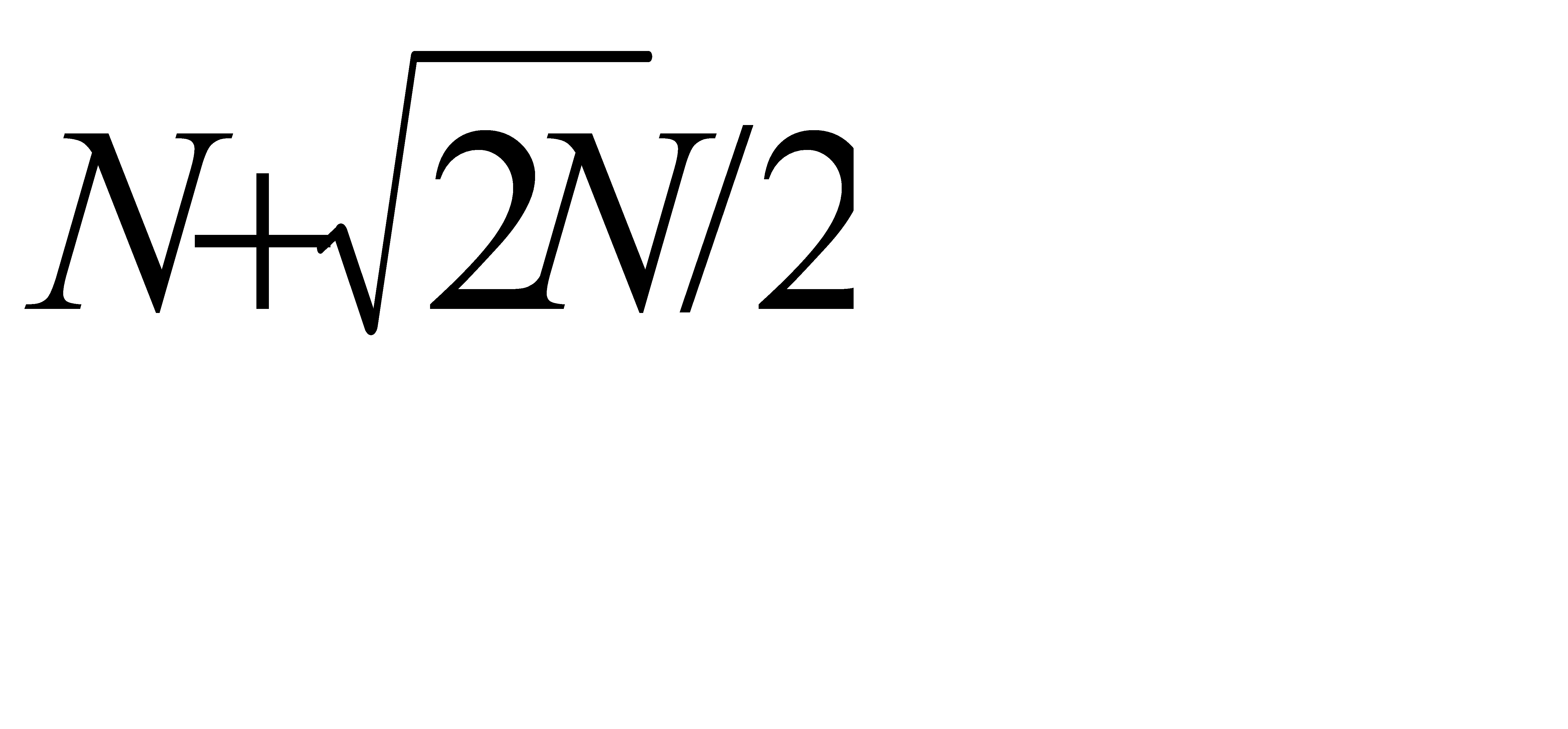 . Вычислим
. Вычислим 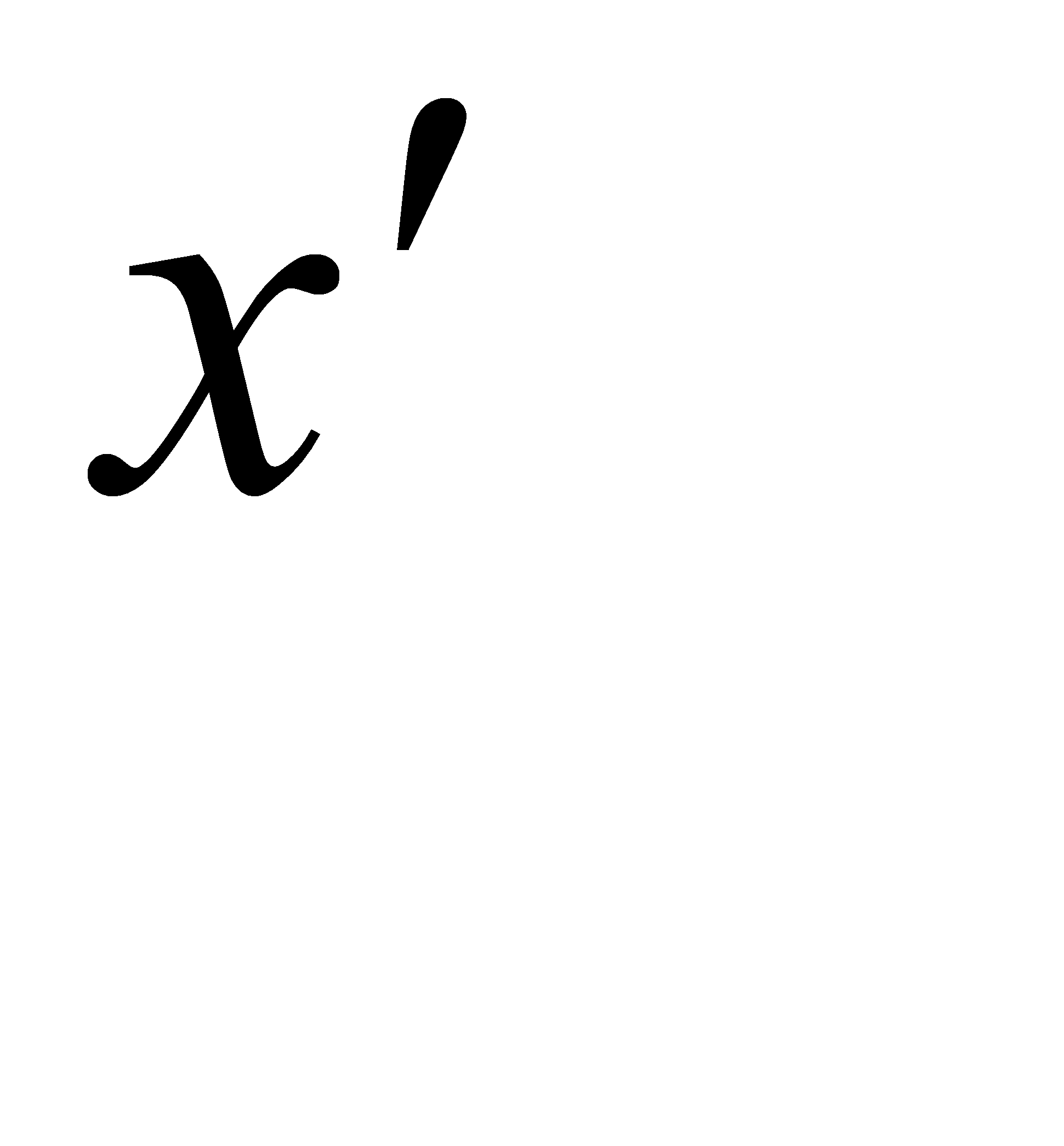 и
и 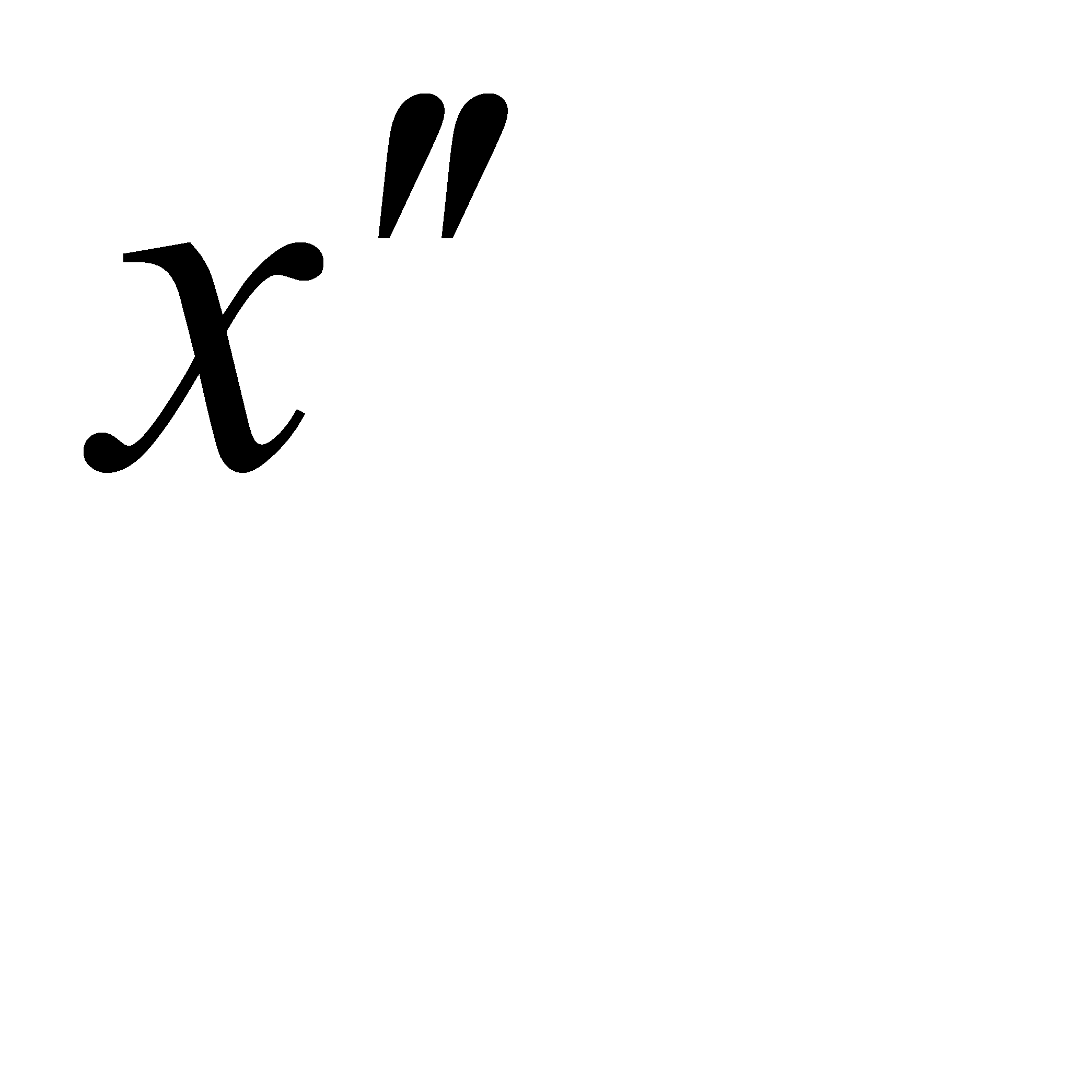 :
: 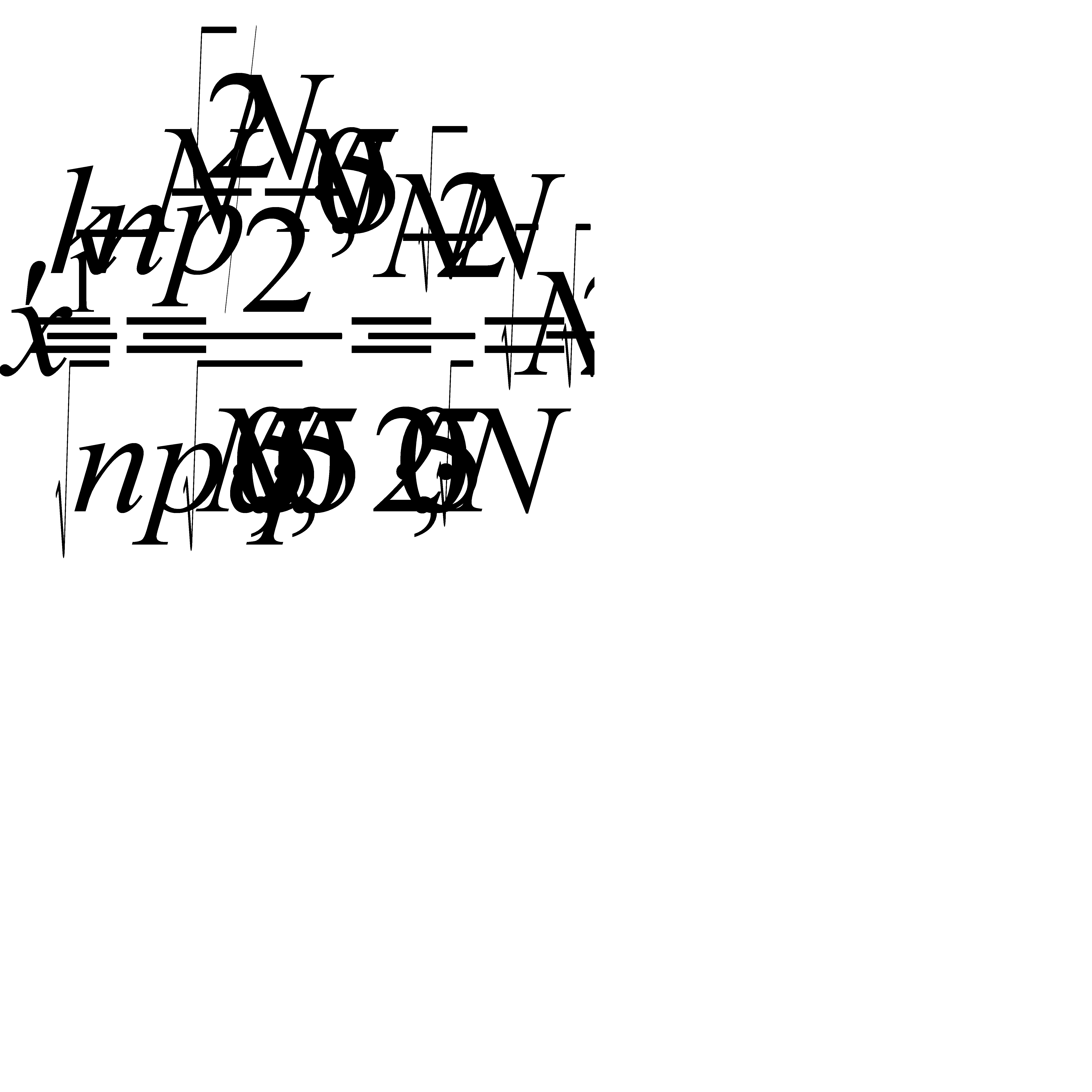 ,
, 
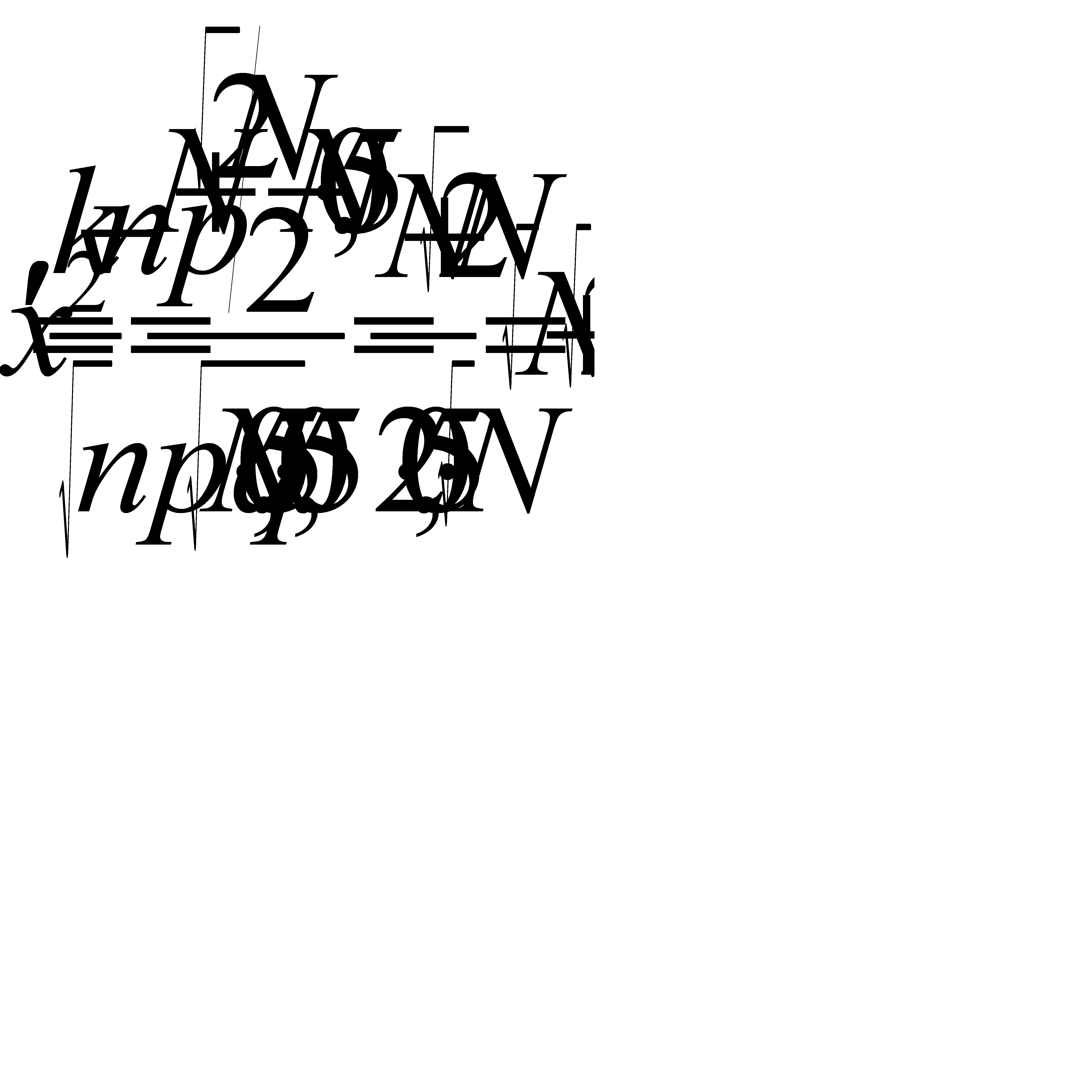
Итак, получаем: 
#129 По условию: 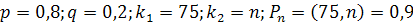
Воспользуемся интегральной теоремой Лапласа: 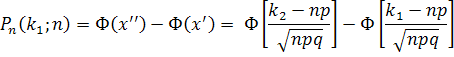
Подставляя данные задачи в формулу, получим 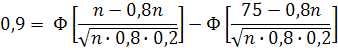
Или 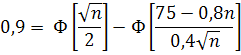
Очевидно, число испытаний 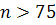 , поэтому
, поэтому 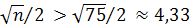 Поскольку функция Лапласа — возрастающая и
Поскольку функция Лапласа — возрастающая и 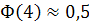 , то можно положить
, то можно положить 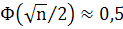 . Следовательно,
. Следовательно, 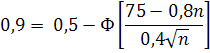
Таким образом, 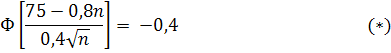
По таблице приложения 2 найдем 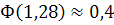 . Отсюда и из соотношения (*), учитывая, что функция Лапласа нечетная, получим
. Отсюда и из соотношения (*), учитывая, что функция Лапласа нечетная, получим 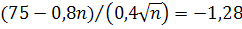 Решив это уравнение, как квадратное относительно
Решив это уравнение, как квадратное относительно 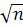 получим
получим 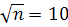 . Следовательно, искомое число испытаний
. Следовательно, искомое число испытаний 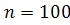 .
.
#131По условию, 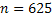 ;
; 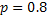 ;
; 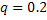 ;
; 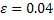 . Требуется найти вероятность
. Требуется найти вероятность 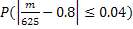 . Воспользуемся формулой
. Воспользуемся формулой 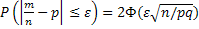 имеем=
имеем= 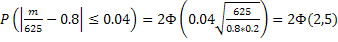 .
.
По таблице приложения 2 найдем 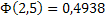 . Следовательно,
. Следовательно, 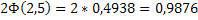 . Итак, искомая вероятность приближенно равна 0, 9876.
. Итак, искомая вероятность приближенно равна 0, 9876.
#132 По условию: n = 900; p = 0, 5; q = 0, 5; ε = 0, 02; Требуется найти вероятность: Pm900- 0, 5≤ 0, 02. Воспользуемся формулой: Pmn- p≤ ε =2ϕ ε npqИмеем: Pm900- 0, 5≤ 0, 02 =2ϕ 0, 029000, 5*0, 5= 2ϕ 1, 2= 0, 7698.
#133По условию, n=10000, p=0, 75, q=0, 25, ε =0, 01Требуется найти вероятность P(|m/10000-0, 75|≤ 0, 01)
Воспользуемся формулой P(|m/n-p|≤ ε )=2Ф(ε * 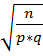 )Получаем P(|m/10000-0, 8|≤ 0, 01)=2Ф(0, 01*
)Получаем P(|m/10000-0, 8|≤ 0, 01)=2Ф(0, 01* 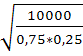 )=2Ф(4/
)=2Ф(4/ 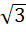 )((4/
)((4/ 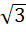 )≈ 2, 31)Ф(4/
)≈ 2, 31)Ф(4/ 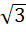 )=0, 4895
)=0, 4895
Следовательно, 2Ф=2*0, 4895=0, 979, ответ: 0, 979
#134n=4040; k=2048; p=0, 5 Воспользуемся формулой P(|mn-p| ≤ ε ) = 2Ф( ε npq ).
ε = |20484040 – 0, 5|= 0, 507 – 0, 5= 0, 007x= 0, 007 *40400, 5*0, 5 = 0, 89Ф(0, 89) = 0, 31332Ф(0, 89) = 0, 6296
#135По условию, р = 0, 5; q = 0, 5; 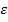 =0, 02; Р (| m/n-0, 5| ≤ 0, 02) = 0, 7698. Воспользуемся формулой Р(|m/n - p| ≤
=0, 02; Р (| m/n-0, 5| ≤ 0, 02) = 0, 7698. Воспользуемся формулой Р(|m/n - p| ≤ 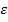 ) = 2Ф (
) = 2Ф ( 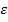
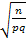 )В силу условия 2Ф (
)В силу условия 2Ф ( 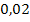
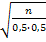 ) = 0, 7698или Ф(0, 04
) = 0, 7698или Ф(0, 04 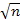 )=0, 3849. По таблице приложения 2 найдем Ф( 1, 2) = 0, 3849. Следовательно, 0, 04
)=0, 3849. По таблице приложения 2 найдем Ф( 1, 2) = 0, 3849. Следовательно, 0, 04 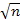 = 1, 2 или
= 1, 2 или 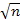 = 30, Таким образом, искомое число испытаний n =900.
= 30, Таким образом, искомое число испытаний n =900.
#136 воспользуемся формулой Р(|m/n - p| ≤ 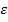 ) = 2Ф (
) = 2Ф ( 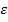
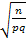 )По условию, р=1/6, q = 5/6,
)По условию, р=1/6, q = 5/6, 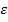 = 0, 01. Вероятность осуществления неравенства, противоположного заданному, т. е. неравенства | m/n- 1/6|
= 0, 01. Вероятность осуществления неравенства, противоположного заданному, т. е. неравенства | m/n- 1/6| 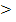 0, 01, равна1- 2Ф (
0, 01, равна1- 2Ф ( 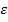
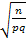 )
)
Согласно условию должно иметь место неравенство 2Ф ( 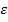
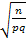 )≥ 1- 2Ф (
)≥ 1- 2Ф ( 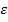
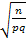 ), или 4Ф (
), или 4Ф ( 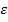
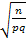 )≥ 1, отсюда Ф (
)≥ 1, отсюда Ф ( 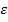
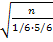 )≥ 0, 25. По таблице приложения 2 найдем Ф(0, 67) =0, 2486; Ф(0, 68) = 0, 2517.
)≥ 0, 25. По таблице приложения 2 найдем Ф(0, 67) =0, 2486; Ф(0, 68) = 0, 2517.
Выполнив линейную интерполяцию, получим Ф (0, 6745) =0, 25. Учитывая соотношение (*) и принимая во внимание, что функция Ф (*)— возрастающая, имеем 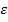
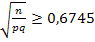 или 0, 01
или 0, 01 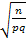 )≥ 0, 6745, Отсюда искомое число бросаний монеты n≥ 632.
)≥ 0, 6745, Отсюда искомое число бросаний монеты n≥ 632.
#137По условию, р = 0, 2; q = 0, 8; 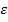 =0, 04; Воспользуемся формулой Р(|m/n - p| ≤
=0, 04; Воспользуемся формулой Р(|m/n - p| ≤ 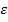 ) = 2Ф (
) = 2Ф ( 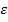
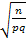 )
)
Получим Р(|m/n – 0, 2| ≤ 0, 04 ) = 2Ф (0, 04 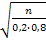 )2Ф (0, 04
)2Ф (0, 04 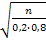 )=0, 99 или Ф(0, 1
)=0, 99 или Ф(0, 1 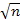 )=0, 495. По таблице приложения 2 найдем Ф(2, 56) =0, 4948; Ф(2, 58) = 0, 4951
)=0, 495. По таблице приложения 2 найдем Ф(2, 56) =0, 4948; Ф(2, 58) = 0, 4951
Выполнив линейную интерполяцию, получим Ф (2, 573) =0, 495.
Следовательно 0, 01 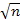 =2, 573Отсюда n=661
=2, 573Отсюда n=661
#138 По условию p=1/5; q=4/5; ξ =0, 01; P=0, 95; n=?. Воспользуемся формулой P( |m/n – p| ≤ ξ )= 2Φ (ξ 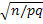 )
)
Из условия P=0. 95=2Φ (ξ 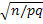 ), отсюда Φ =0, 475, 0, 475=Φ (x)= Φ (ξ
), отсюда Φ =0, 475, 0, 475=Φ (x)= Φ (ξ 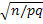 ), Φ =0, 475 соответствует значение x=1, 95 ( из Приложения 2), тогдаx=1. 95= ξ
), Φ =0, 475 соответствует значение x=1, 95 ( из Приложения 2), тогдаx=1. 95= ξ 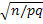 =0, 01 *
=0, 01 * 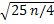 =0, 025
=0, 025 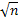 n=6147в) если число пр—целое, то наивероятнейшее число ko = np.
n=6147в) если число пр—целое, то наивероятнейшее число ko = np.
#139Решение: По условию, n=400, p=0, 8, q=0, 2. Следовательно, 
По таблице приложения 2 найдём 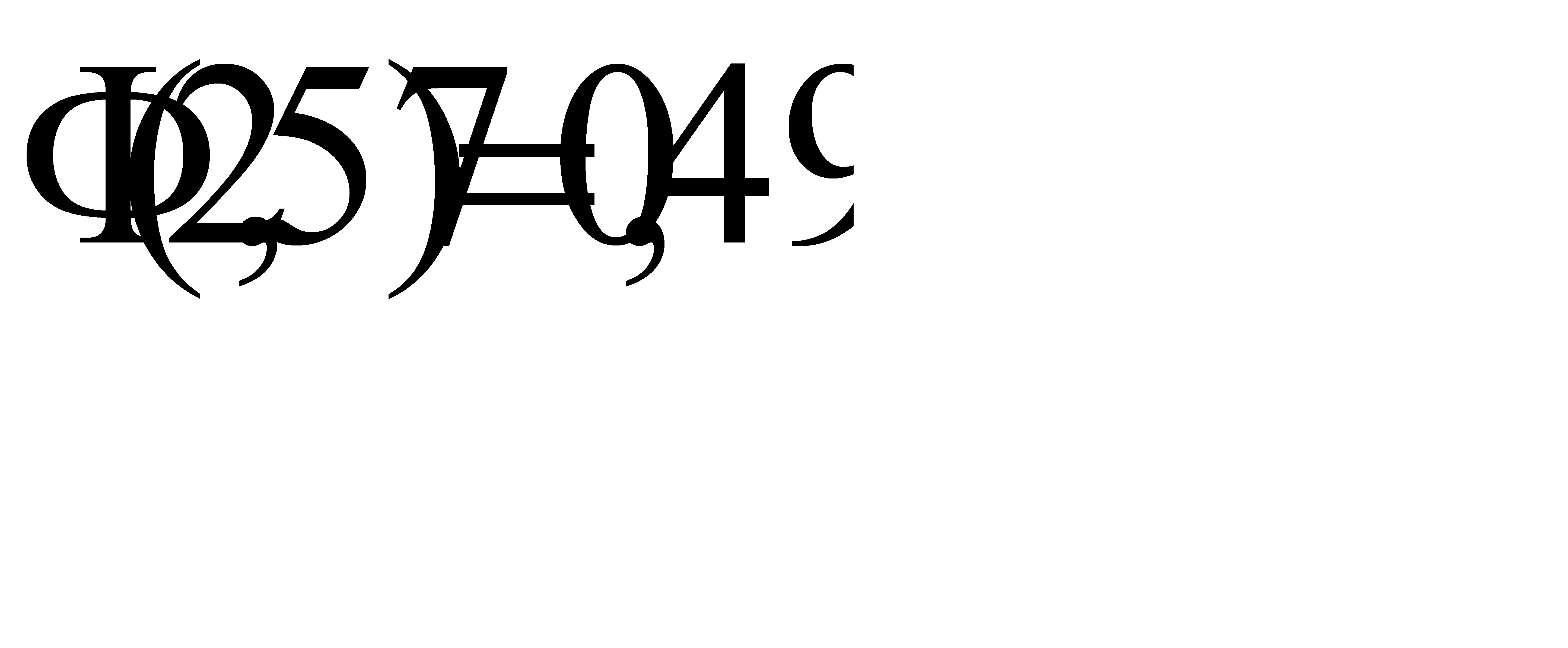 , значит
, значит 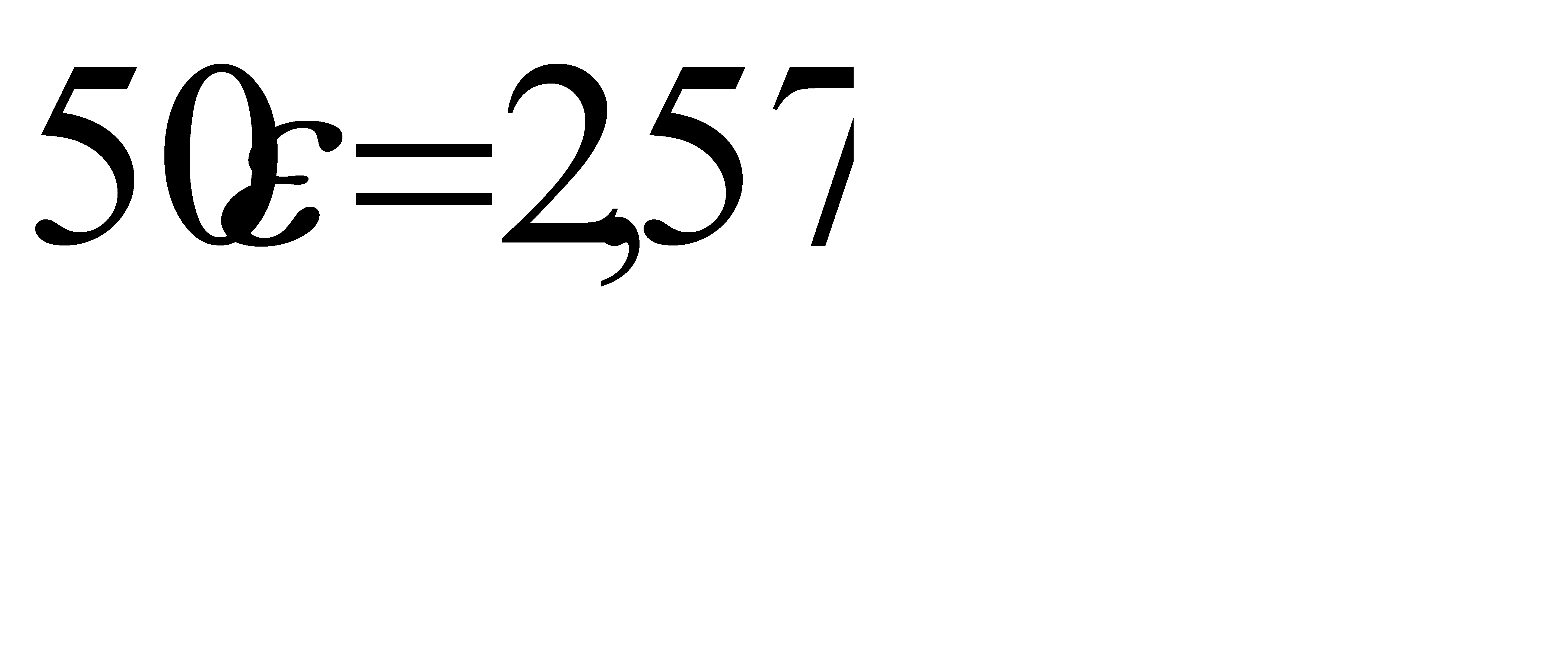 ,
, 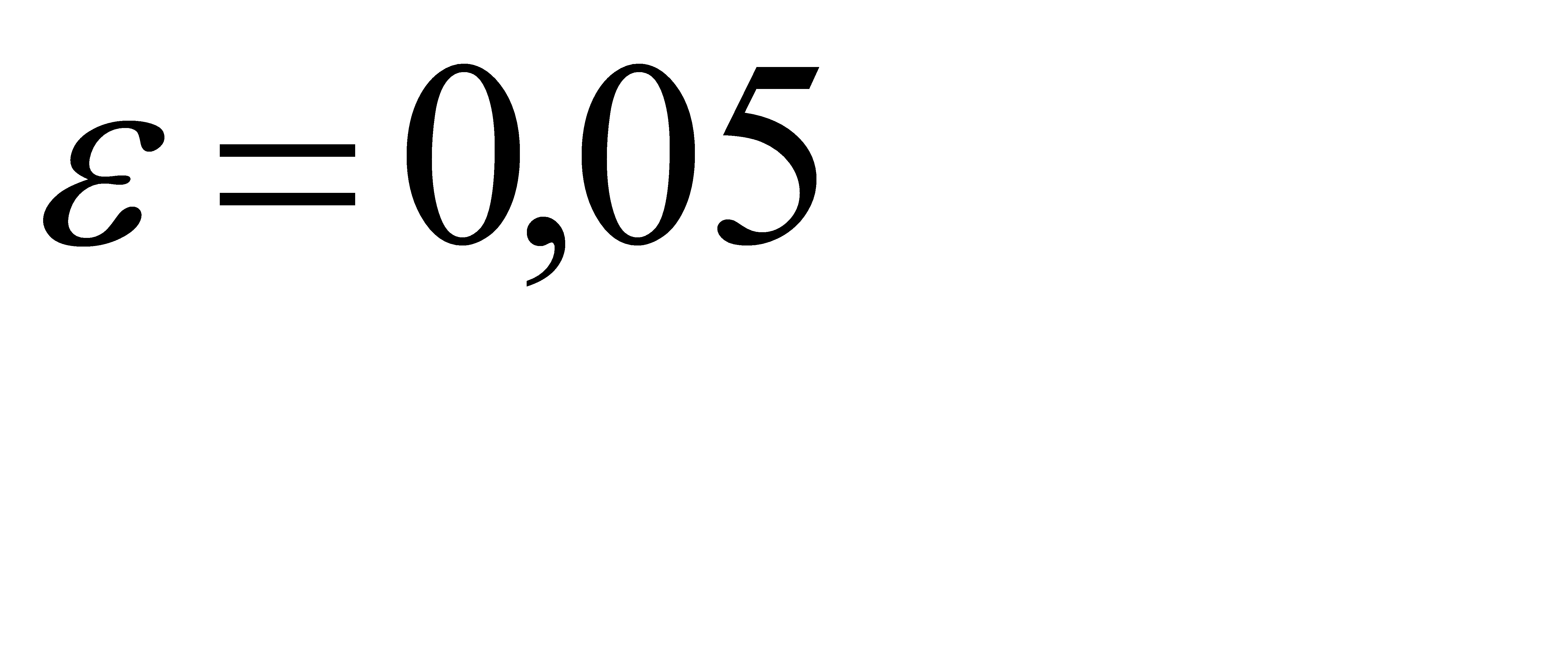 Ответ:
Ответ: 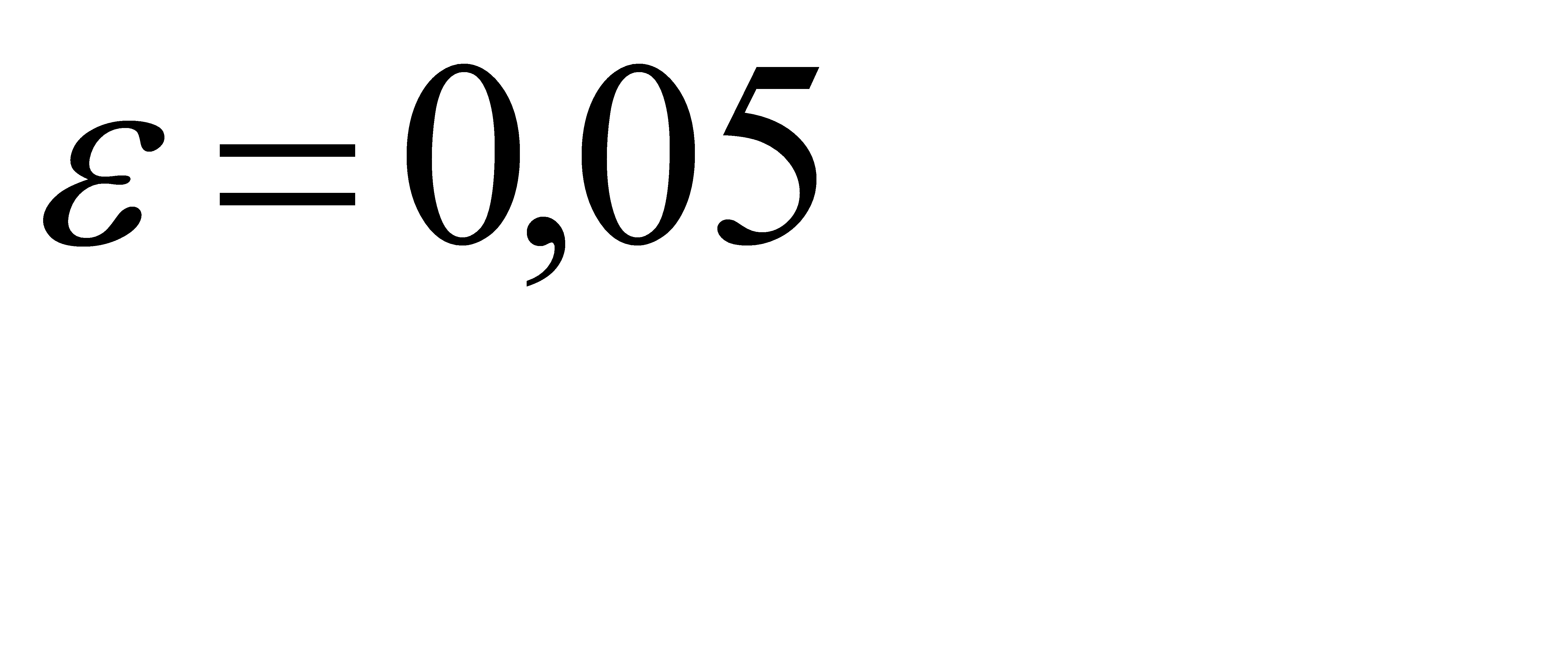
#140По условию, 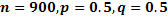 . Следовательно,
. Следовательно, 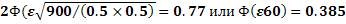
По таблице приложения 2 найдем 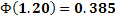 , значит
, значит 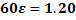 . Отсюда искомое число
. Отсюда искомое число 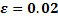 .
.
#141По условию, n = 10 000, p = 0, 75, q = 0, 25. Следовательно,
2Ф (ε 10 000/(0, 75*0, 25)) = 0, 98 или Ф (231*ε ) = 0, 49. Т. к. Ф(2, 34) = 0, 49, значит 231*ε = 2, 34. искомое число ε = 0, 01.
#142Решение: По условию, n=900, p=0, 9, q=0, 1. Следовательно, 
По таблице приложения 2 найдём 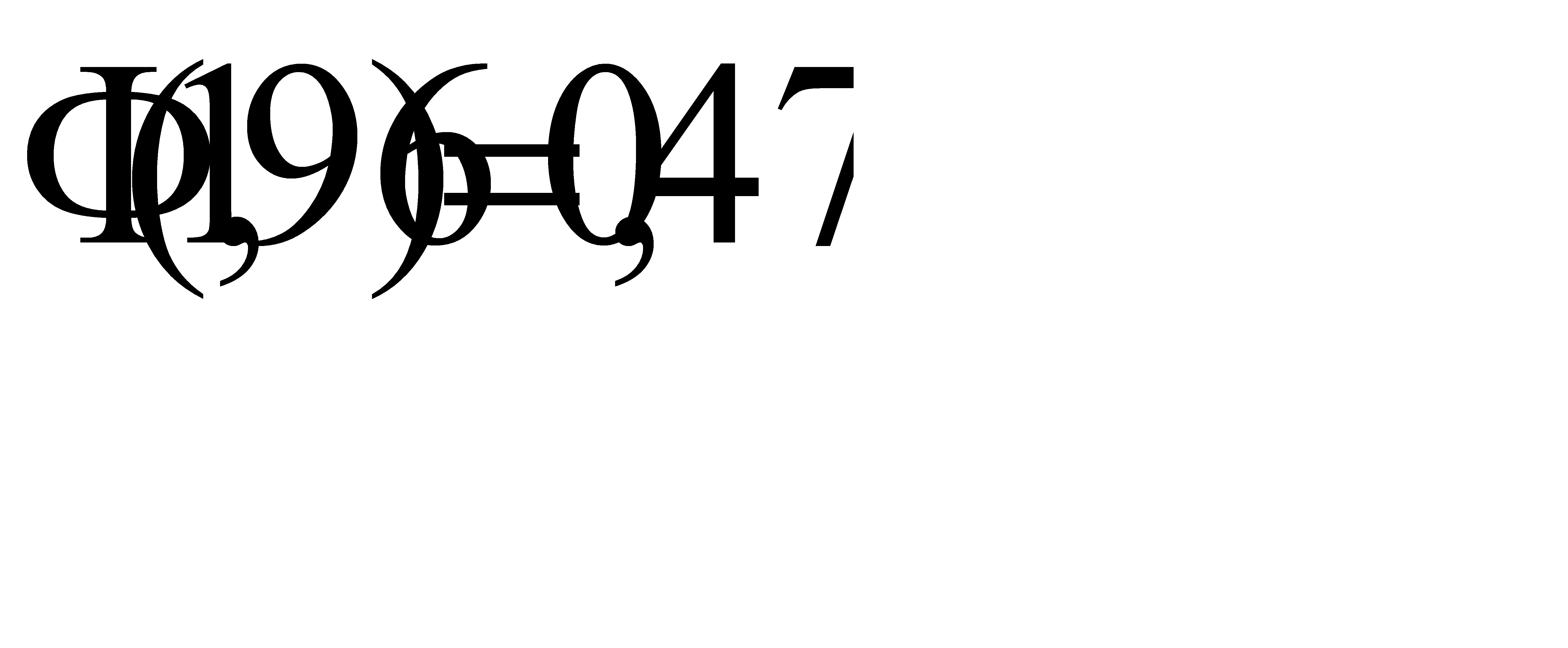 , значит
, значит 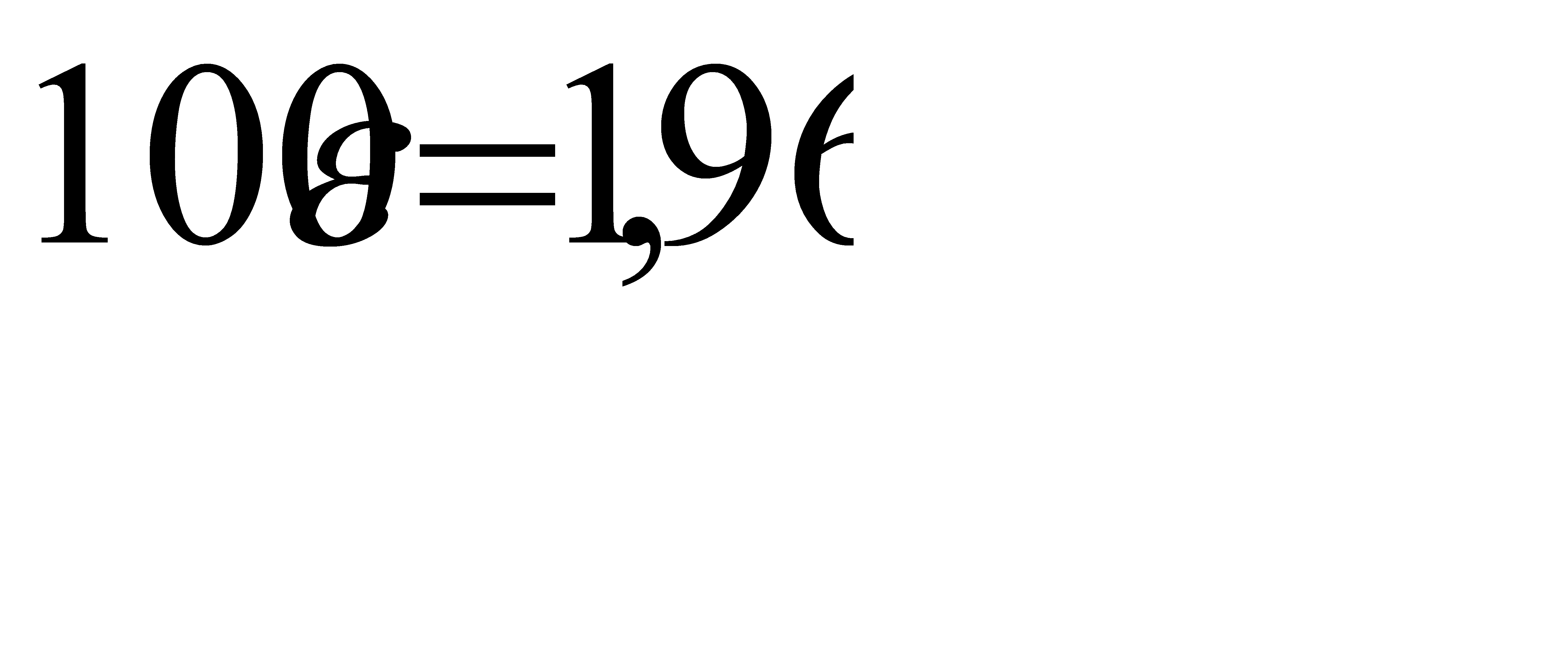 . Отсюда
. Отсюда 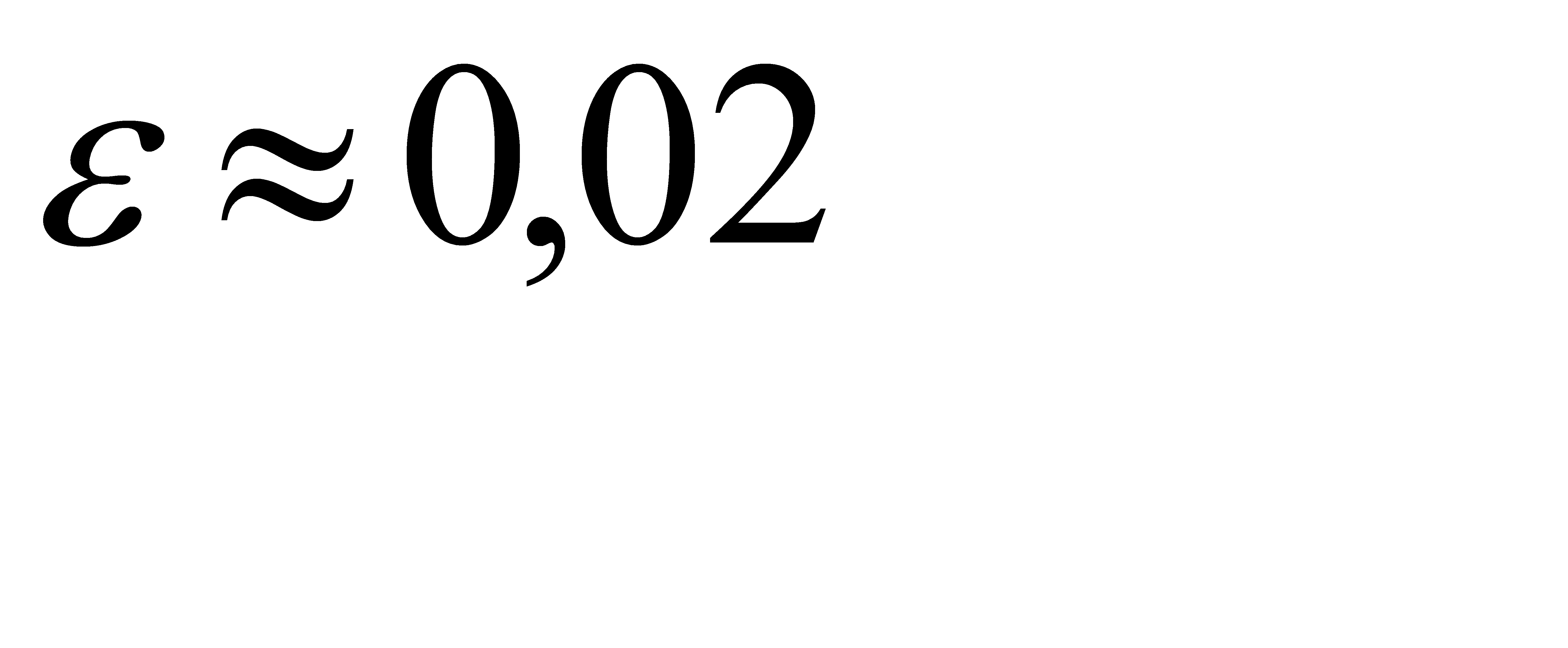 .
.
Таким образом, с вероятностью 0, 95 отклонение относительной частоты стандартных деталей от вероятности 0, 9 удовлетворяет неравенству 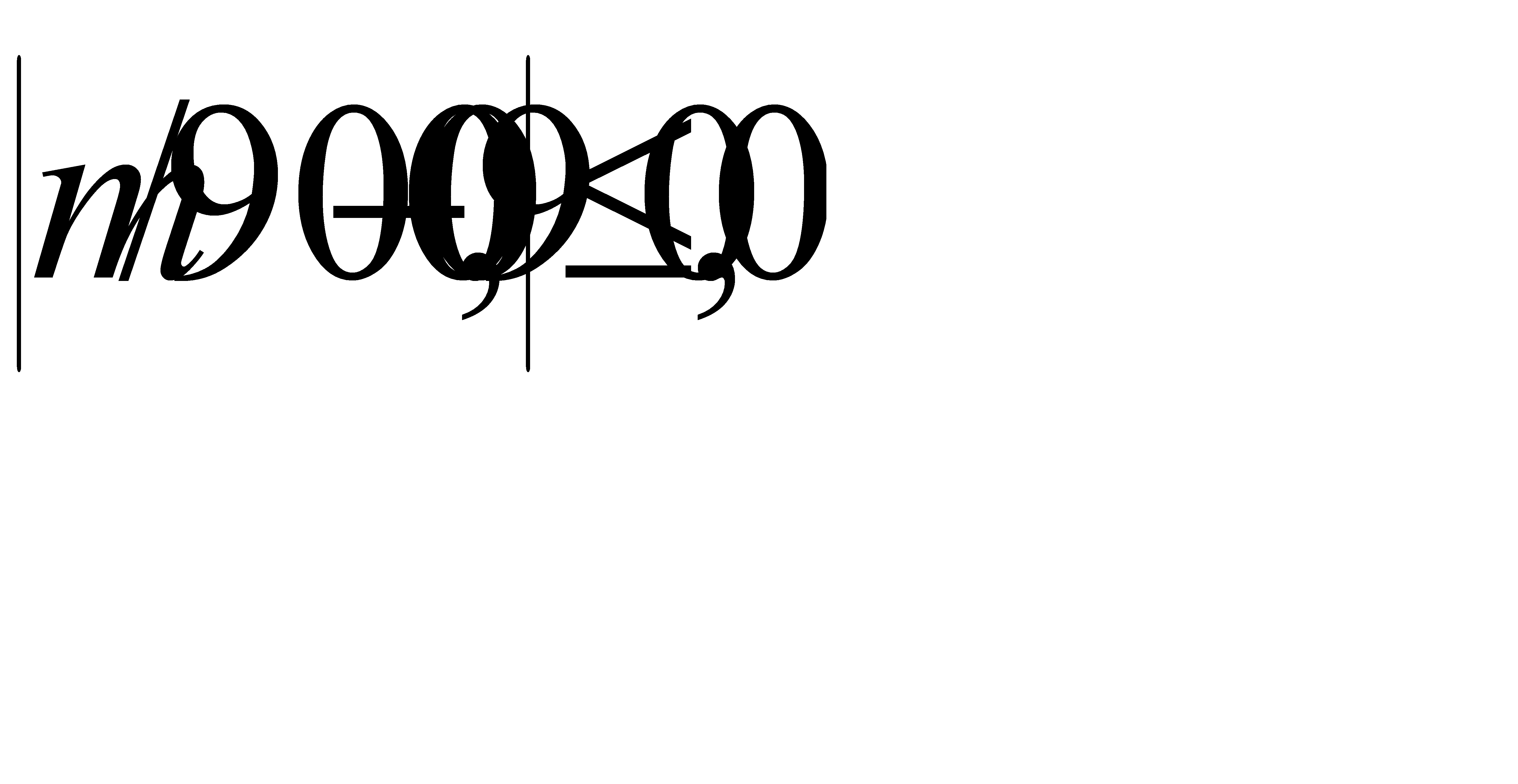 ,
, 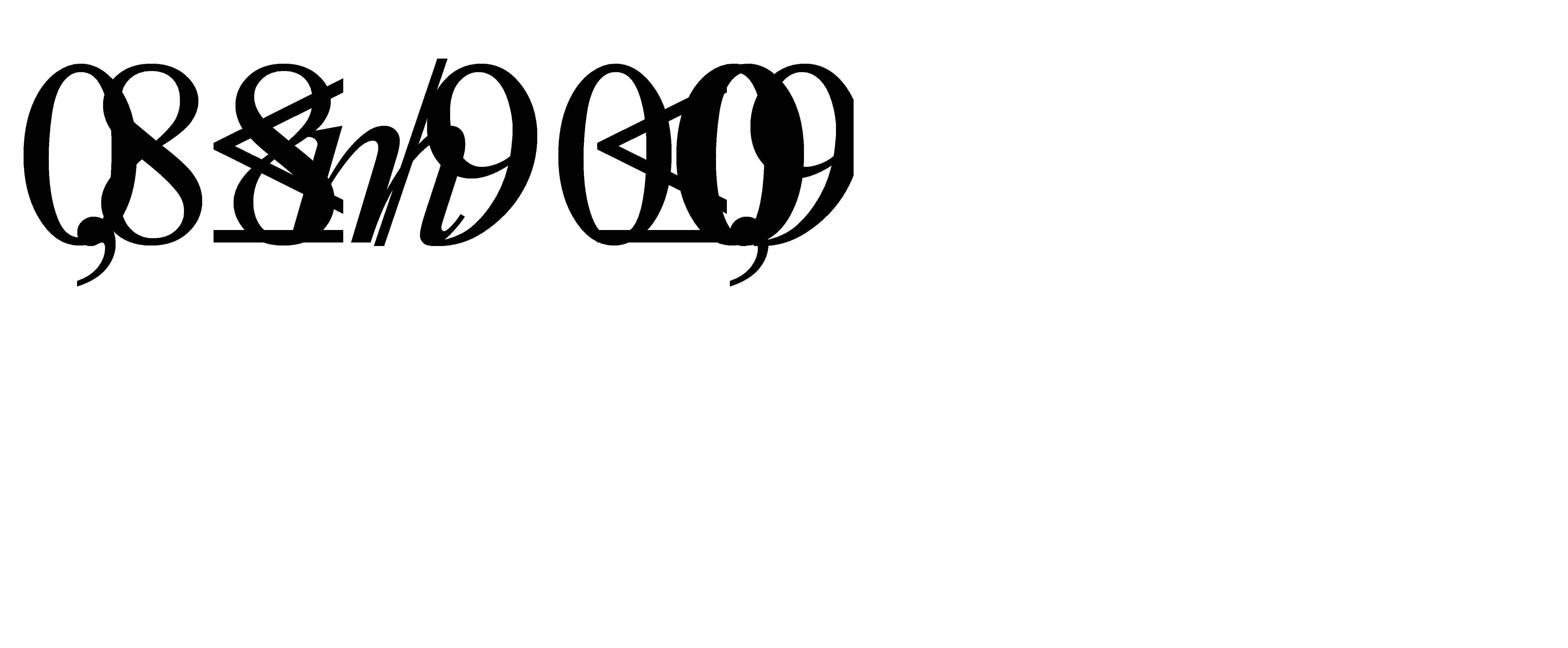
Отсюда искомое число m стандартных деталей среди 900 проверенных с вероятностью 0, 95 заключено в следующих границах 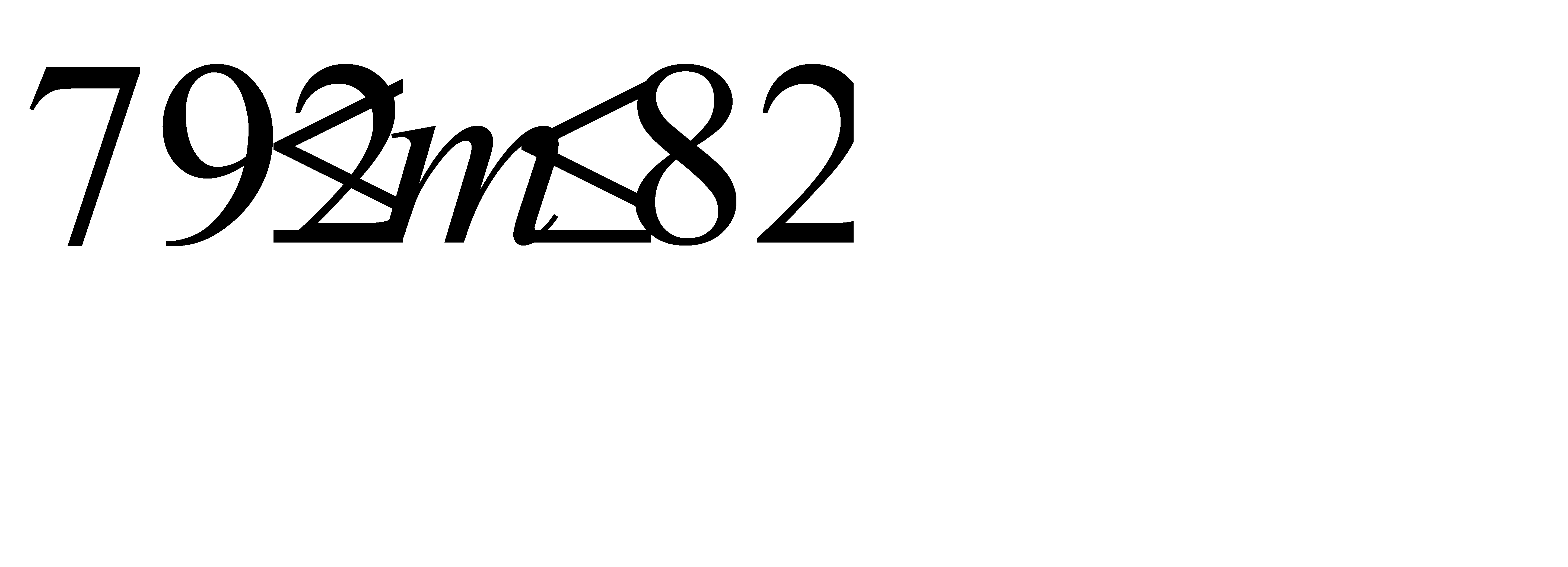 . Ответ:
. Ответ:  .
.
#143Решение: По условию, n=475, p=0, 05, q=0, 95. Следовательно, 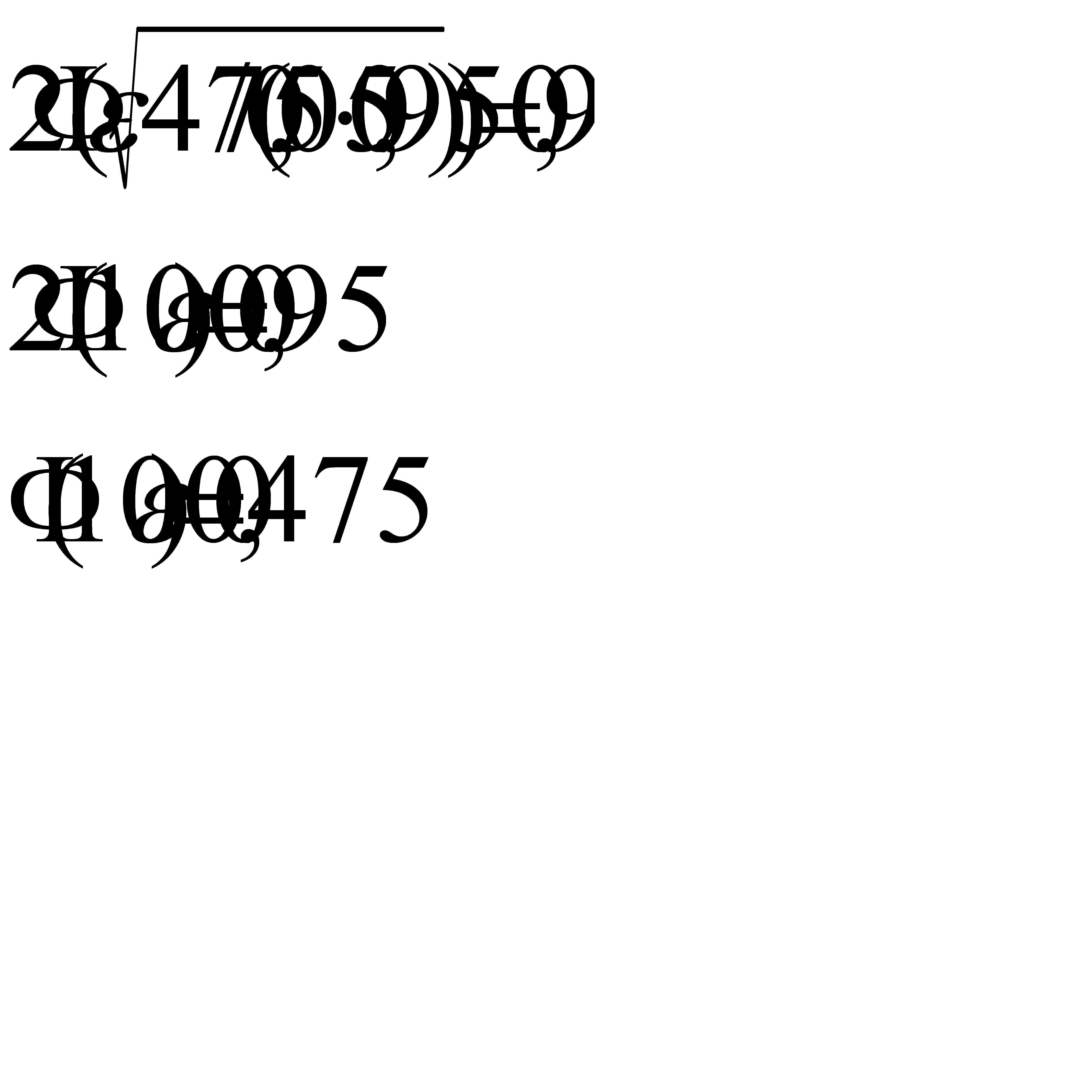
По таблице приложения 2 найдём 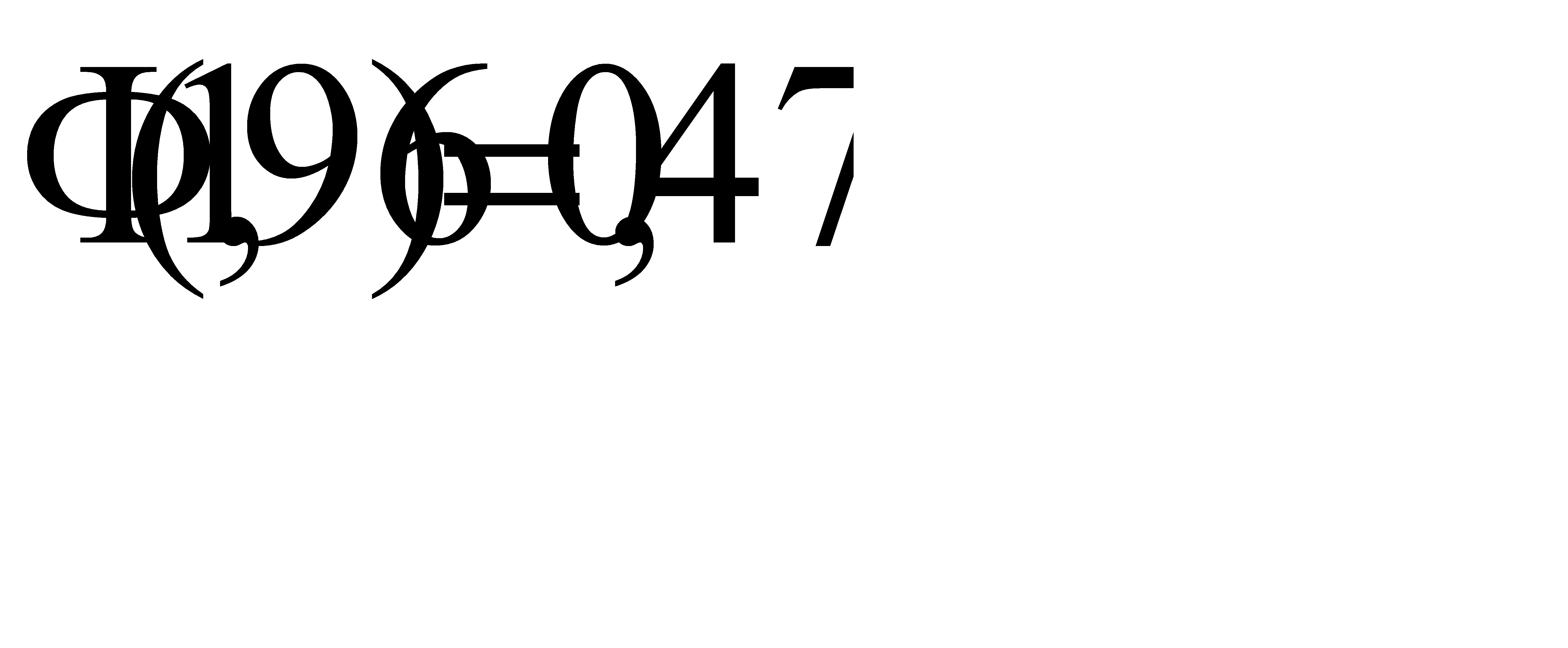 , значит
, значит 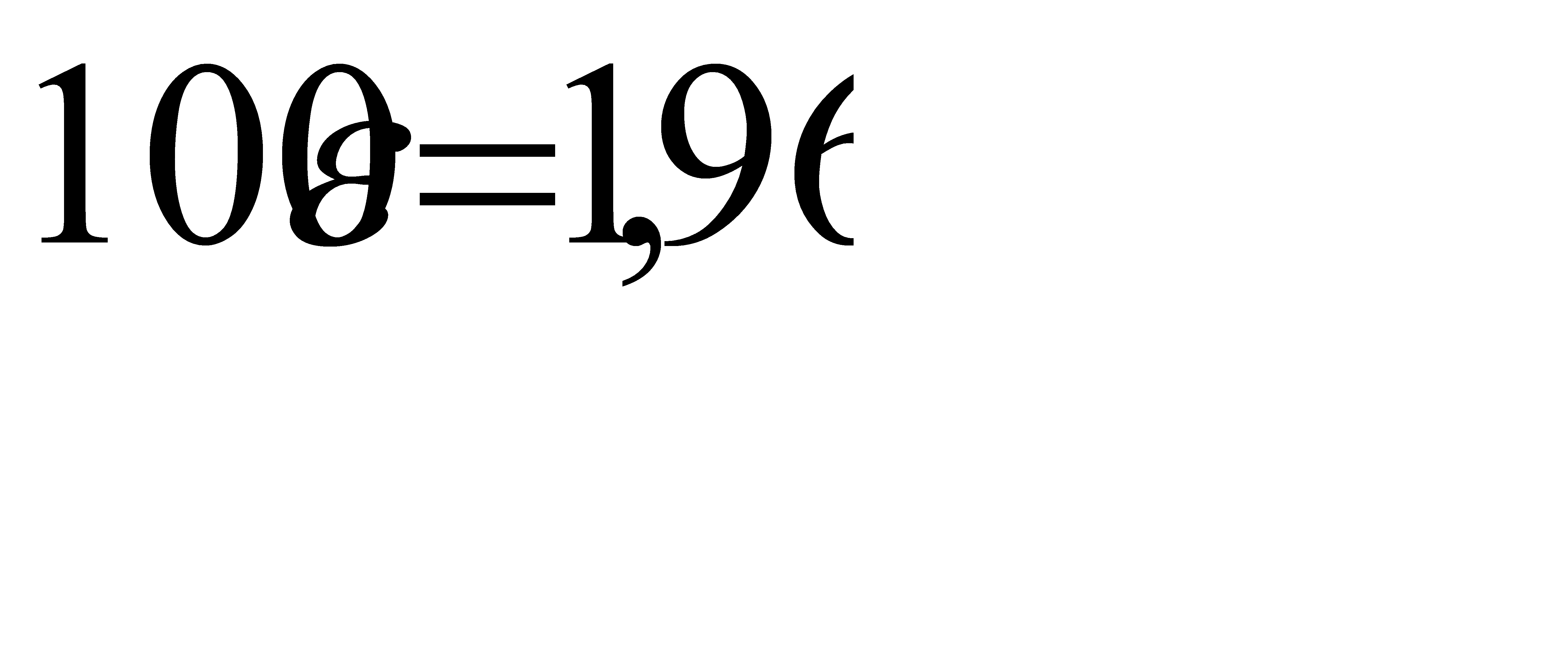 . Отсюда
. Отсюда 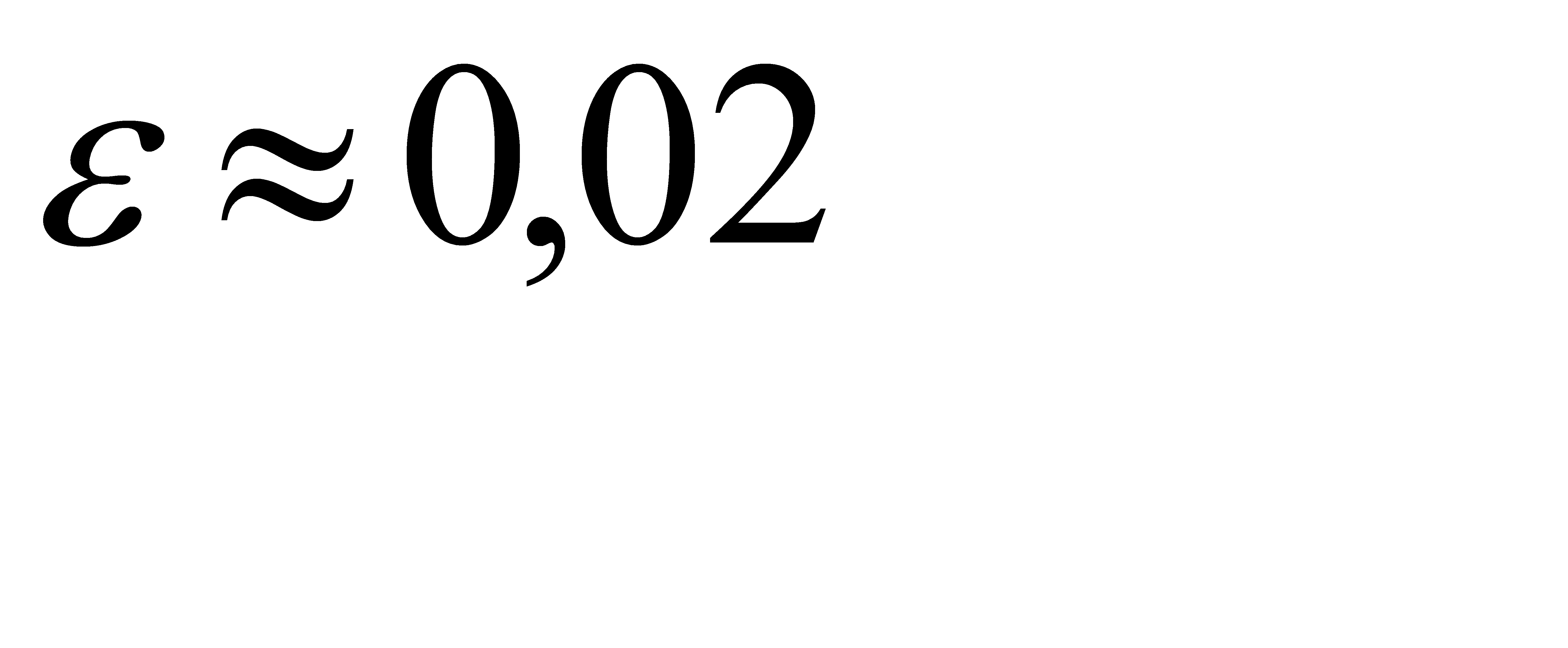 .
.
Таким образом, с вероятностью 0, 95 отклонение относительной частоты бракованных изделий от вероятности 0, 05 удовлетворяет неравенству 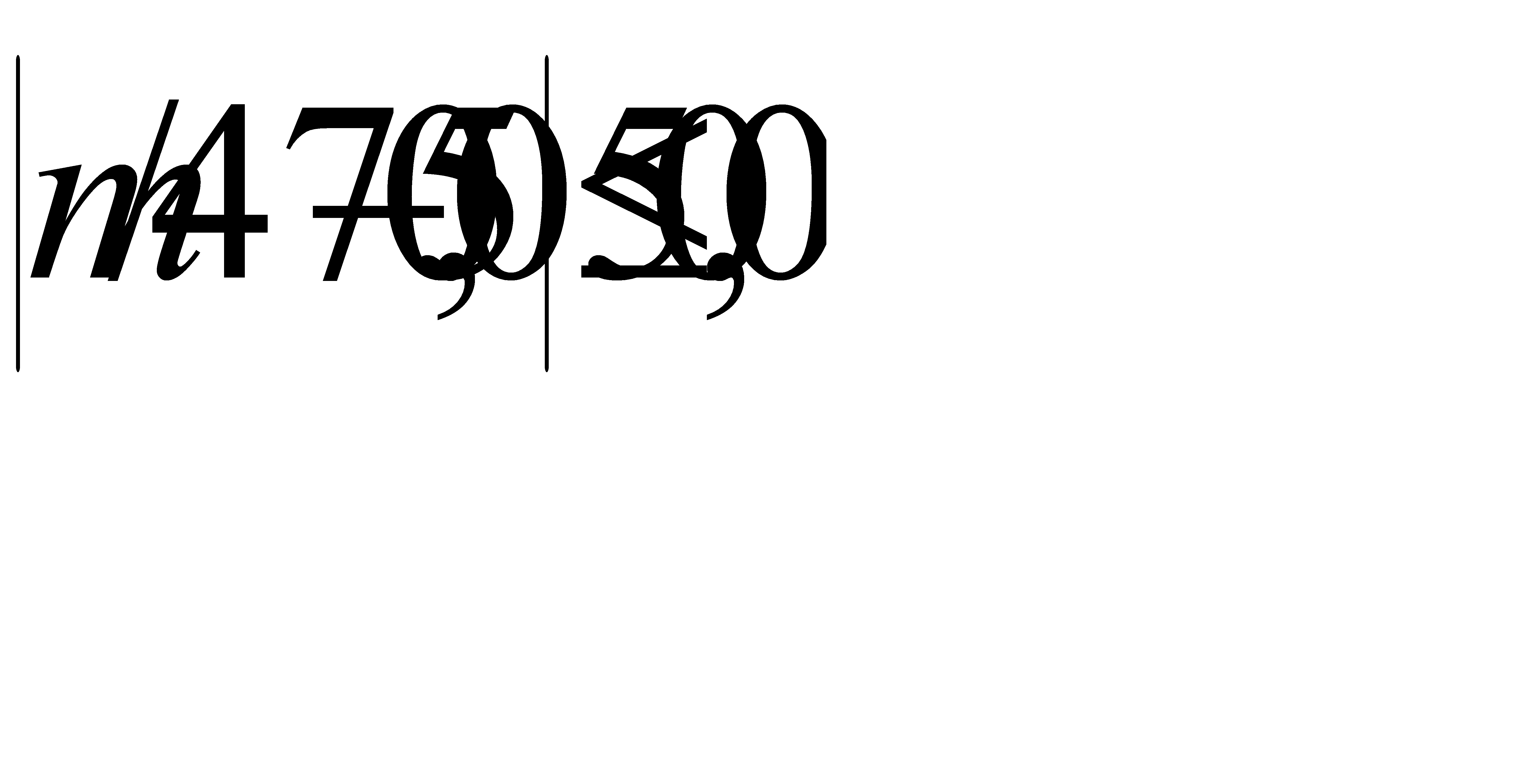

Отсюда искомое число m бракованных изделий среди 475 проверенных с вероятностью 0, 95 заключено в следующих границах 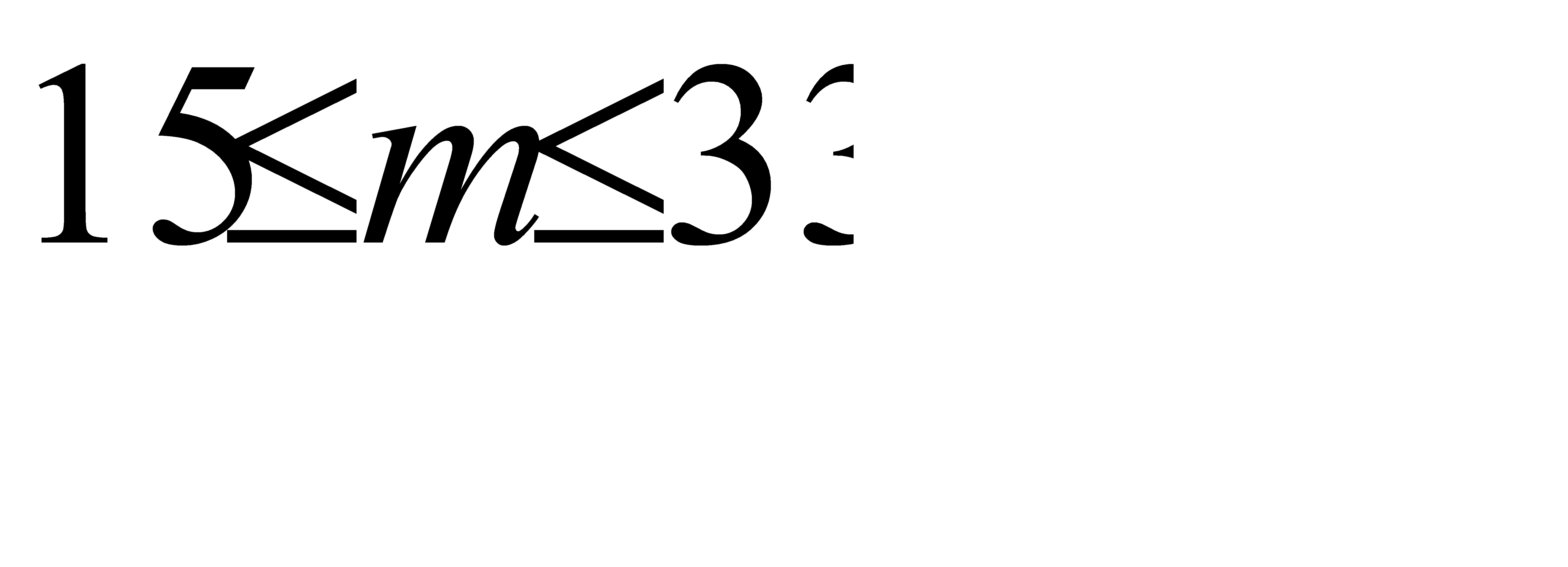 . Ответ:
. Ответ: 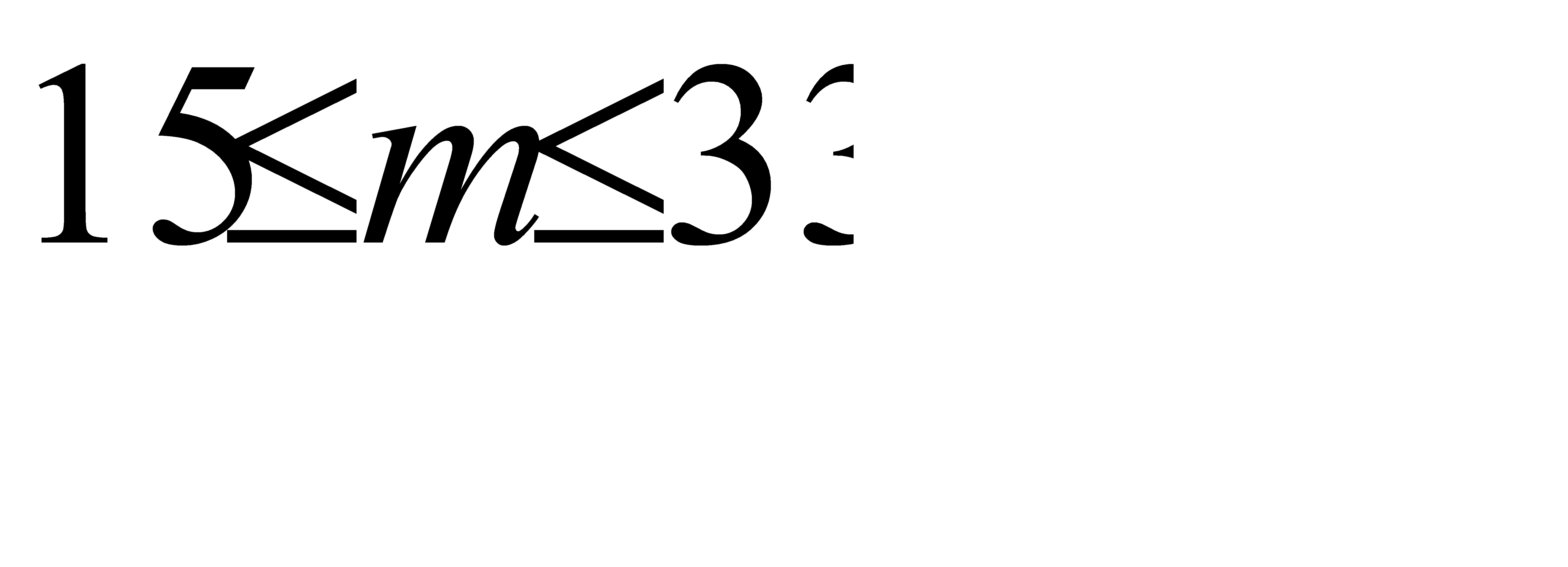 .
.
#144 По условию, n=80, p=1/6, q=5/6. Следовательно, 
По таблице приложения 2 найдём 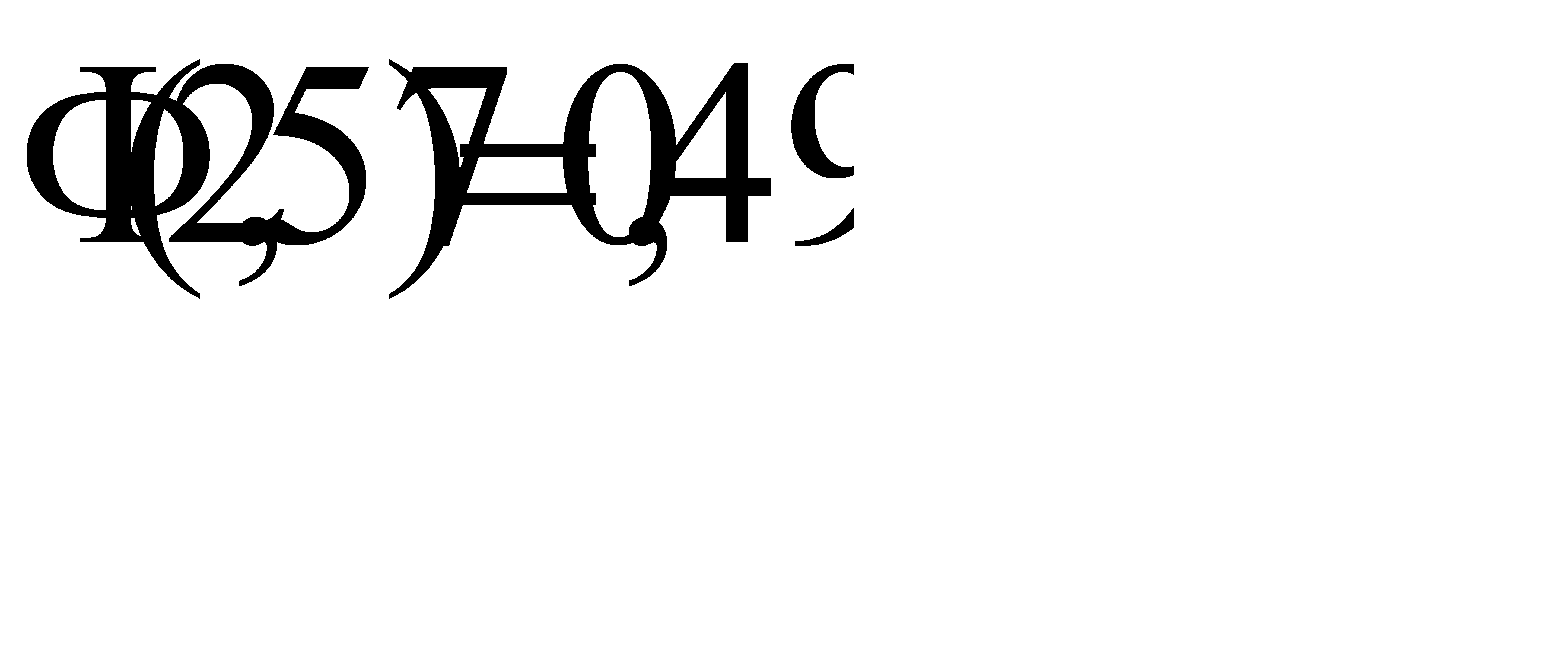 , значит
, значит 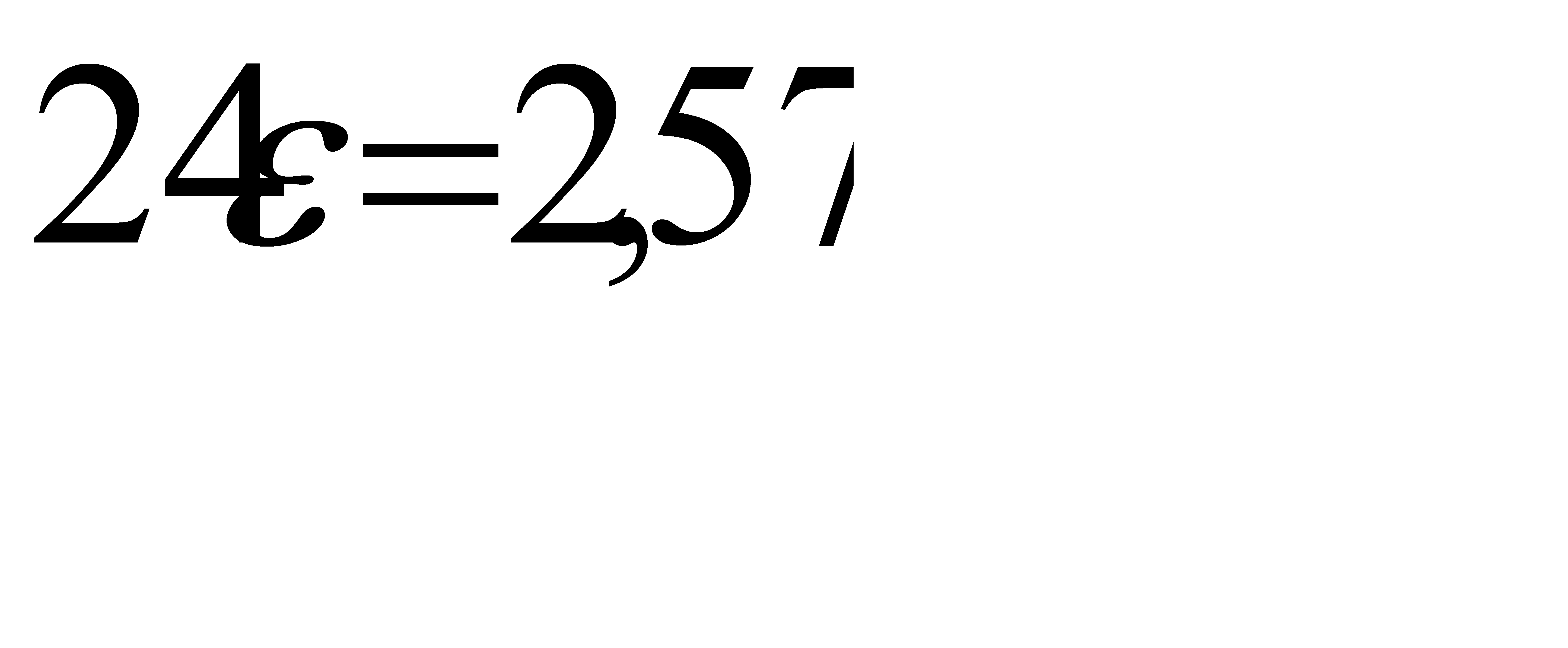 . Отсюда
. Отсюда 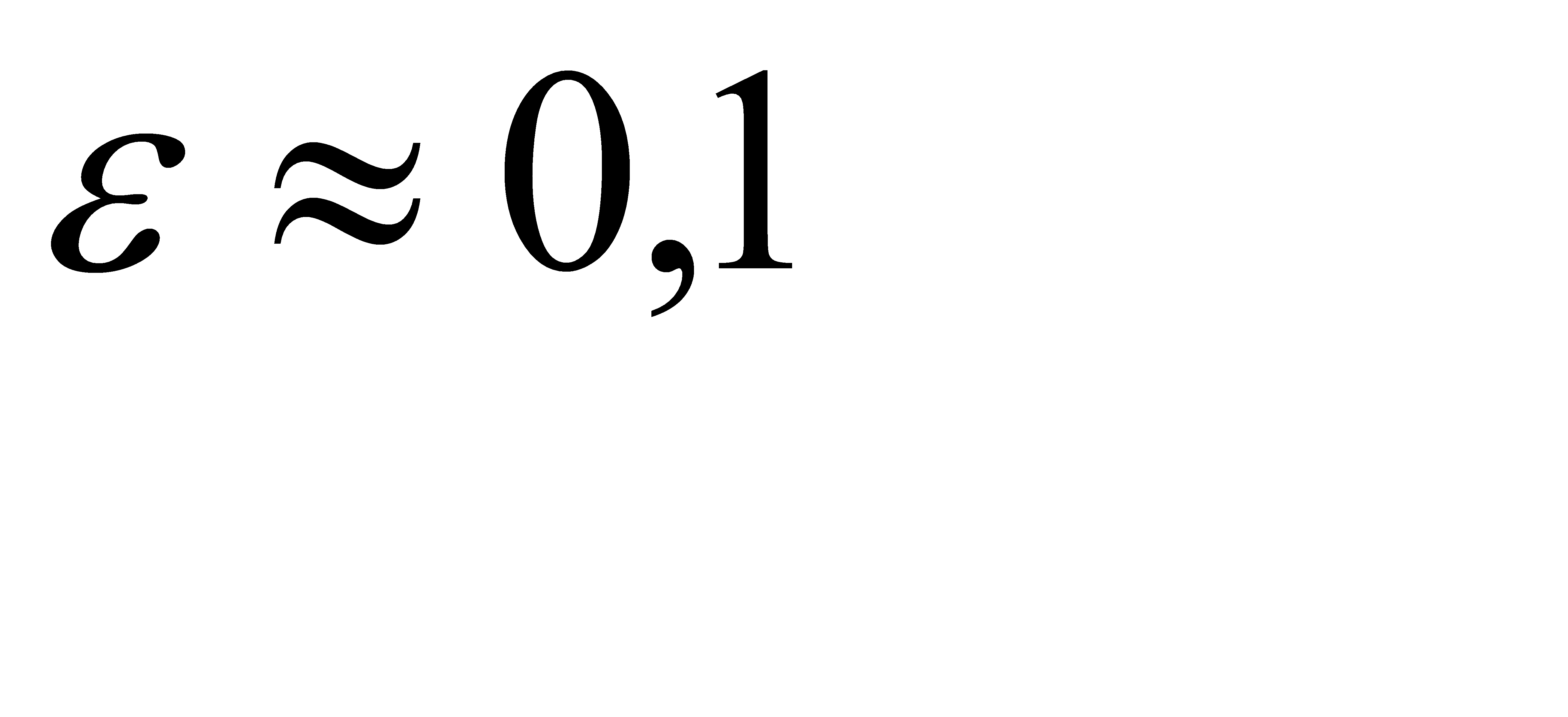 .
.
Таким образом, с вероятностью 0, 99 отклонение относительной частоты выпадения шестёрки от вероятности 1/6 удовлетворяет неравенству 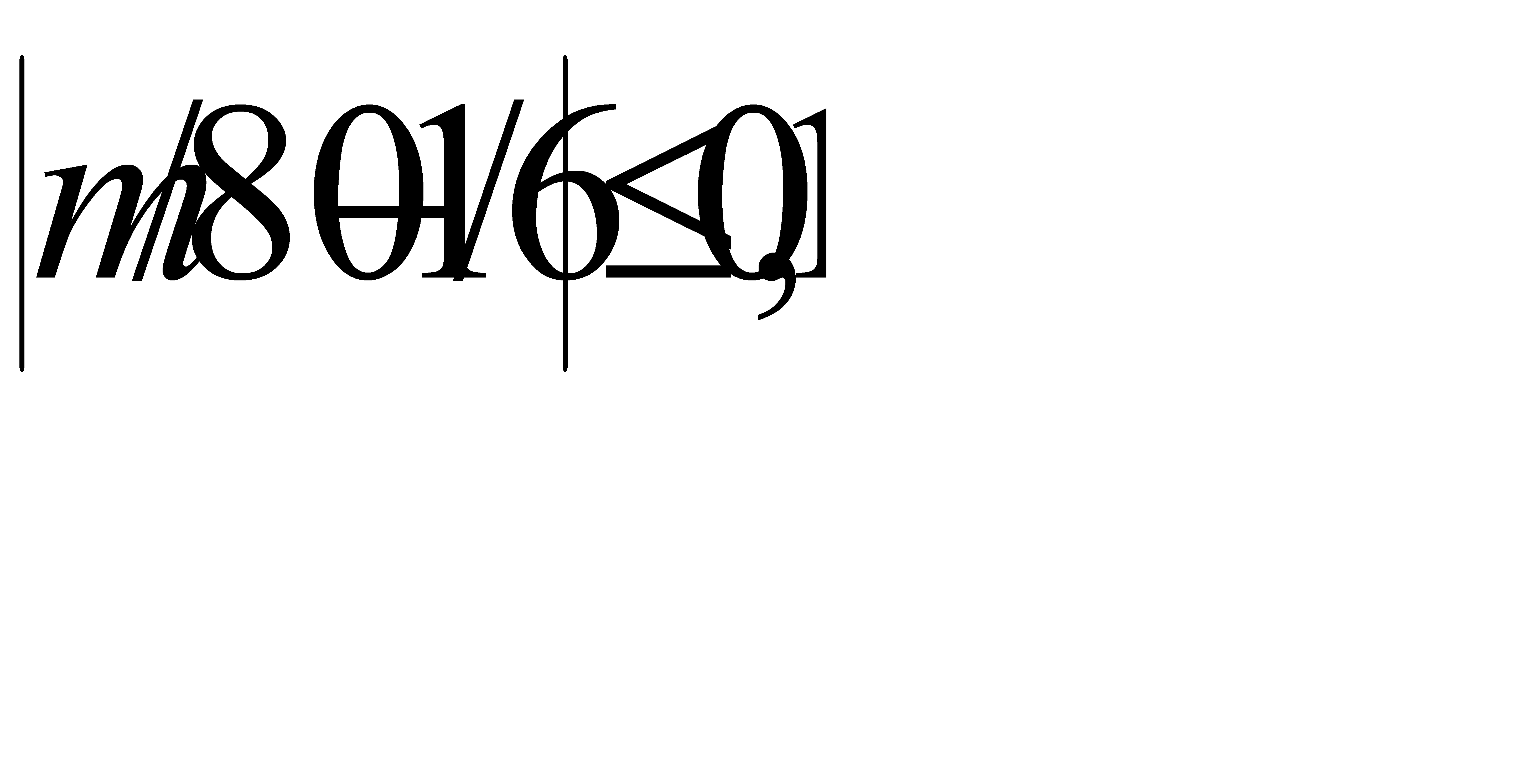
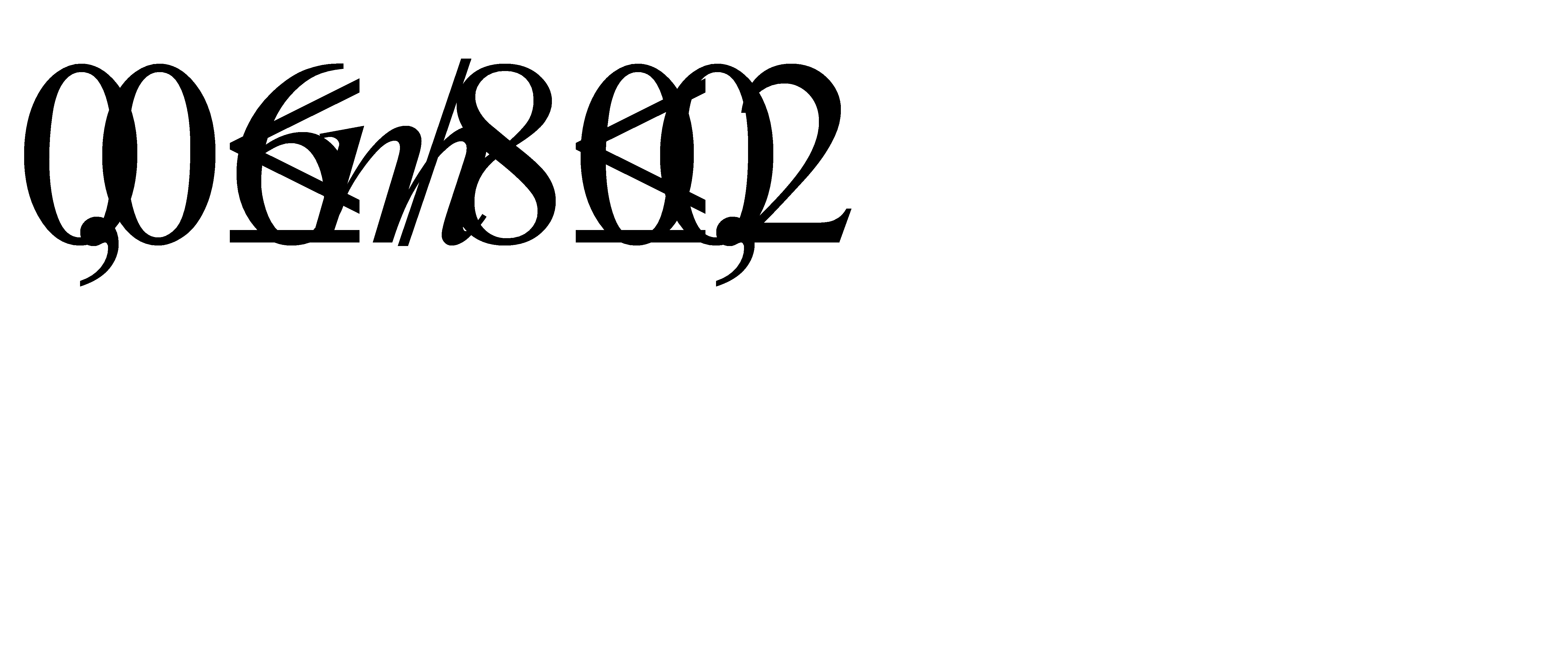 , Отсюда искомое число m испытаний среди 80 с вероятностью 0, 99 заключено в следующих границах
, Отсюда искомое число m испытаний среди 80 с вероятностью 0, 99 заключено в следующих границах 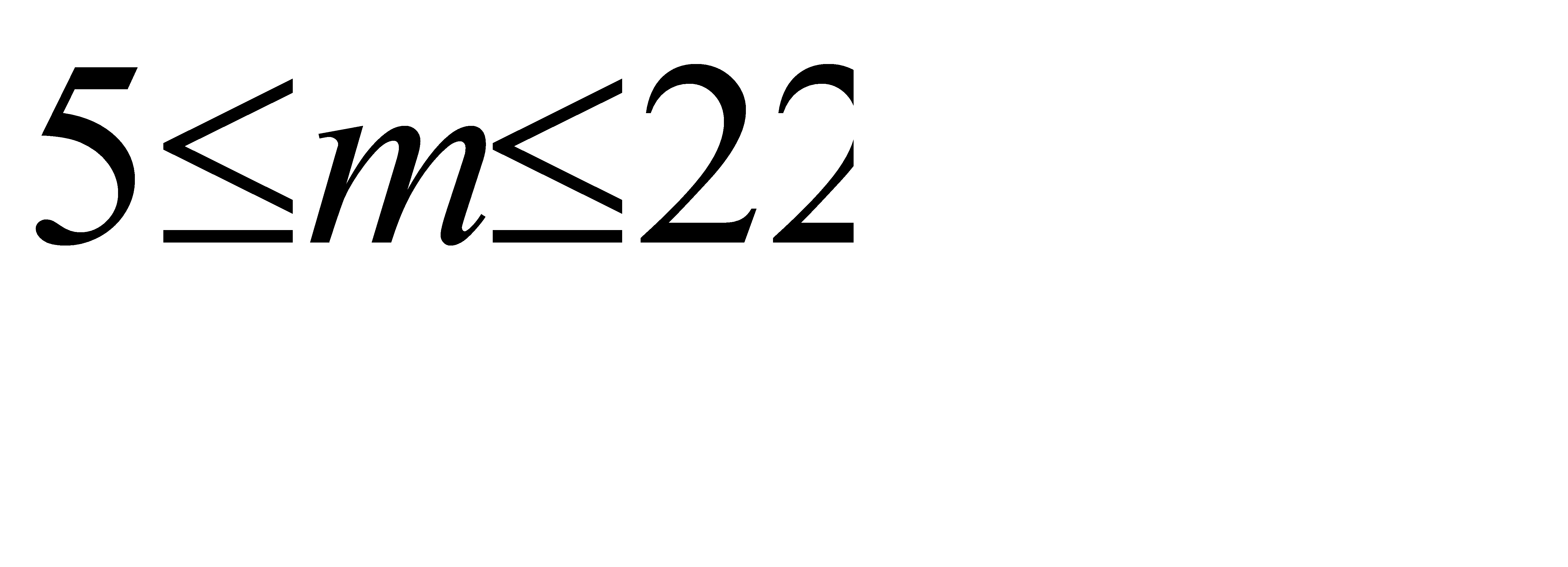 . Ответ:
. Ответ: 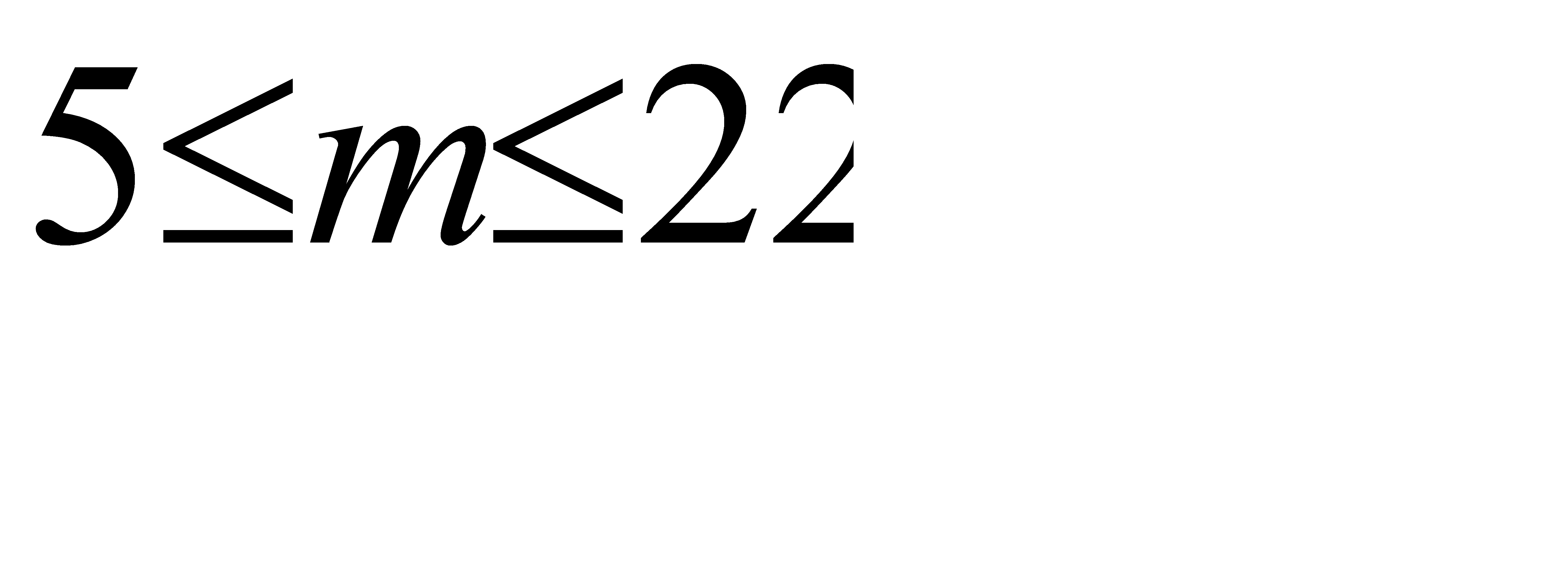 .
.
#145Решение: По условию, 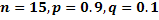 . Найдем наивероятнейшее число
. Найдем наивероятнейшее число 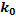 из двойного неравенства:
из двойного неравенства:
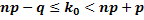 Подставив данные задачи, получим:
Подставив данные задачи, получим:
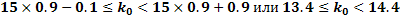
Так как 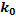 – целое число и поскольку между числами
– целое число и поскольку между числами 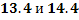 заключено одно целое число, а именно
заключено одно целое число, а именно 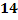 , то искомое наивероятнейшее число
, то искомое наивероятнейшее число 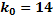
#146 По условию n=10; p=0, 75; q=1-p=0, 25. Найдем наивероятнейшее число деталей из неравенства: np-q ≤ k0 < np+p
Подставив значение получим: 10*0, 75-0, 25 ≤ k0 < 10*0, 75+0, 757, 25 ≤ k0 < 8, 25
Только одно целое число удовлетворяет неравенству. Это число 8. K0=8
#147По условию, n=24; p=0, 6; q=0, 4. Найдем наивероятнейшее число годных к продаже образцов товаров из двойного неравенства 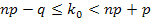 . Подставляя данные задачи,
. Подставляя данные задачи, 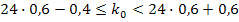 , или
, или 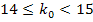 . Так как
. Так как 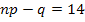 – целое число, то и наивероятнейших чисел два:
– целое число, то и наивероятнейших чисел два: 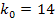 и
и 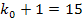 .
.
#148По условию, n=19; p=0, 9; q=0, 1. Найдем наивероятнейшее число правильно набитых перфокарт из двойного неравенства np-q< =k0< np+p. Подставляя данные задачи, получим
19*0, 9-0, 1< = k0< 19*0, 9+0, 1 или 17< = k0< 17, 2. Так как np-q=17 – целое число, то наивероятнейшее число k0=17.
#149
Решение: Известно, что если произведение числа испытаний n на вероятность р появления события в одном испытании есть целое число, то наивероятнейшее число 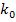 = np.
= np.
В рассматриваемой задаче число испытаний n равно числу сыгранных партий 2N; вероятность появления события равна вероятности выигрыша в одной партии, т. е. р = 1/2 (так как по условию противники равносильны).
Поскольку произведение np = 2N 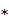 1/2 = N — целое число, то искомое наивероятнейшее число
1/2 = N — целое число, то искомое наивероятнейшее число 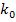 выигранных партий равно N. Ответ: N.
выигранных партий равно N. Ответ: N.
#150 Промахи стрелков есть независимые события, поэтому применима теорема умножения вероятностей независимых событий. Вероятность того, что оба стрелка при одном залпе промахнуться, p=0, 2*0, 4=0, 08.
Поскольку произведение np=25*0, 08=2-целое число, то наивероятнейшее число залпов, при которых не буде ни одного попадания, k0=np=2 ответ: 2.
#151Попадания стрелков есть независимые события, поэтому применима теорема умножения вероятностей независимых событий. Вероятность того, что оба стрелка при одном залпе попадут р=0, 8*0, 6=0, 48, nр=15*0, 48=7, 2, 6, 68< =k0< 7, 68
Наивероятнейшее число залпов, при которых оба стрелка попадут в мишень равно 7.
#152 По условию k0=2; p=0, 4; q=0, 6. Воспользуемся двойным неравенством: np-q≤ k0< np+p.
Подставляя данные задачи, получим систему неравенств для определения неизвестного числа:
0, 4n-0, 6≤ 25; 0, 4n+0, 4> 25. Из первого неравенства системы найдем: n≤ 25, 60, 4=64; Из второго неравенства системы имеем: n> 24, 60, 4=61, 5; Итак, искомое число испытаний должно удовлетворять двойному неравенству: 62≤ n≤ 64.
#153По условию 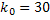 ;
; 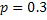 ;
; 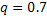 . Воспользуемся двойным неравенством
. Воспользуемся двойным неравенством 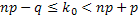
Подставляя данные задачи, получим систему неравенств для определения неизвестного числа:
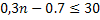 ,
, 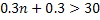 . Из первого неравенства системы найдем
. Из первого неравенства системы найдем 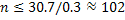 . Из второго неравенства системы найдем
. Из второго неравенства системы найдем 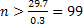 . Итак, искомое число испытаний должно удовлетворить двойному неравенству
. Итак, искомое число испытаний должно удовлетворить двойному неравенству 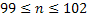 .
.
#155По условию, n=49, k0=30. Воспользуемся двойным неравенством  . Подставляя данные задачи, получим систему неравенств для определения неизвестной вероятности p:
. Подставляя данные задачи, получим систему неравенств для определения неизвестной вероятности p:
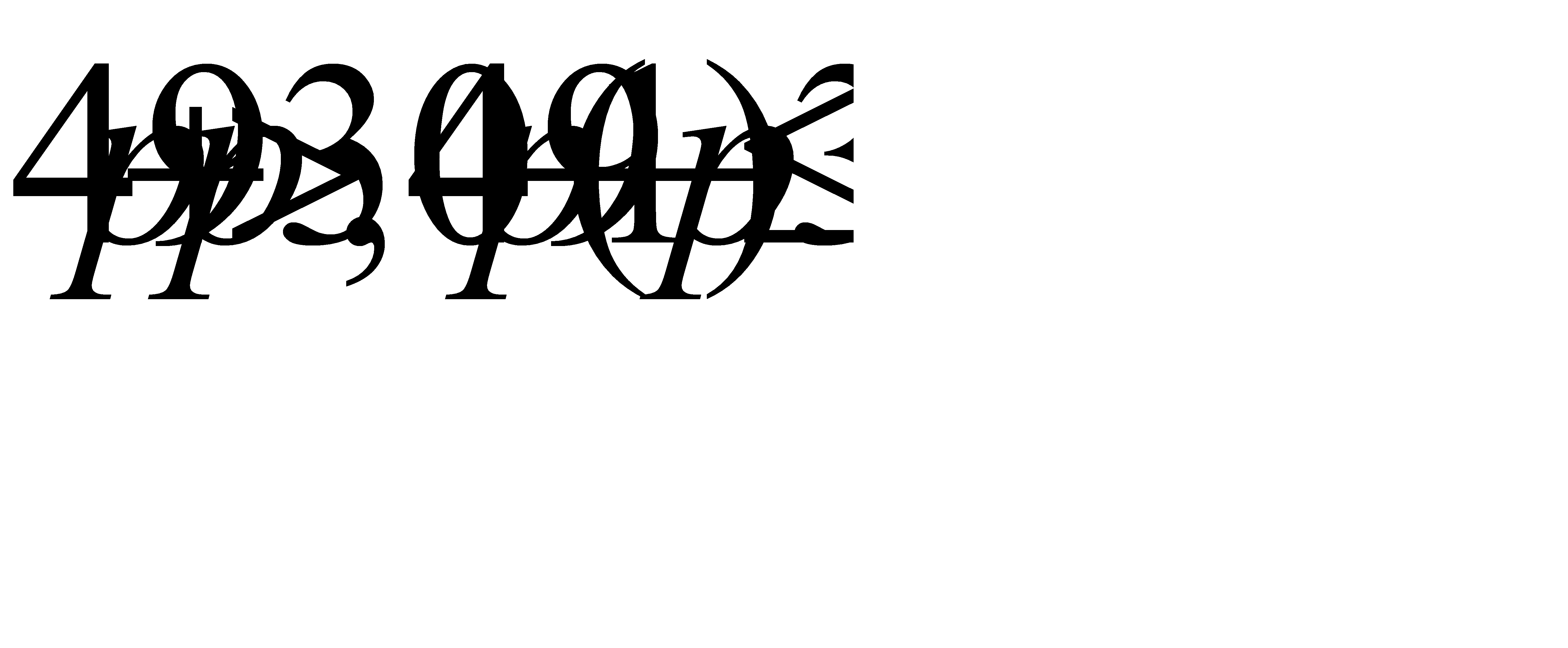 Из первого неравенства системы найдем p> 0, 6. Из второго неравенства системы найдем
Из первого неравенства системы найдем p> 0, 6. Из второго неравенства системы найдем 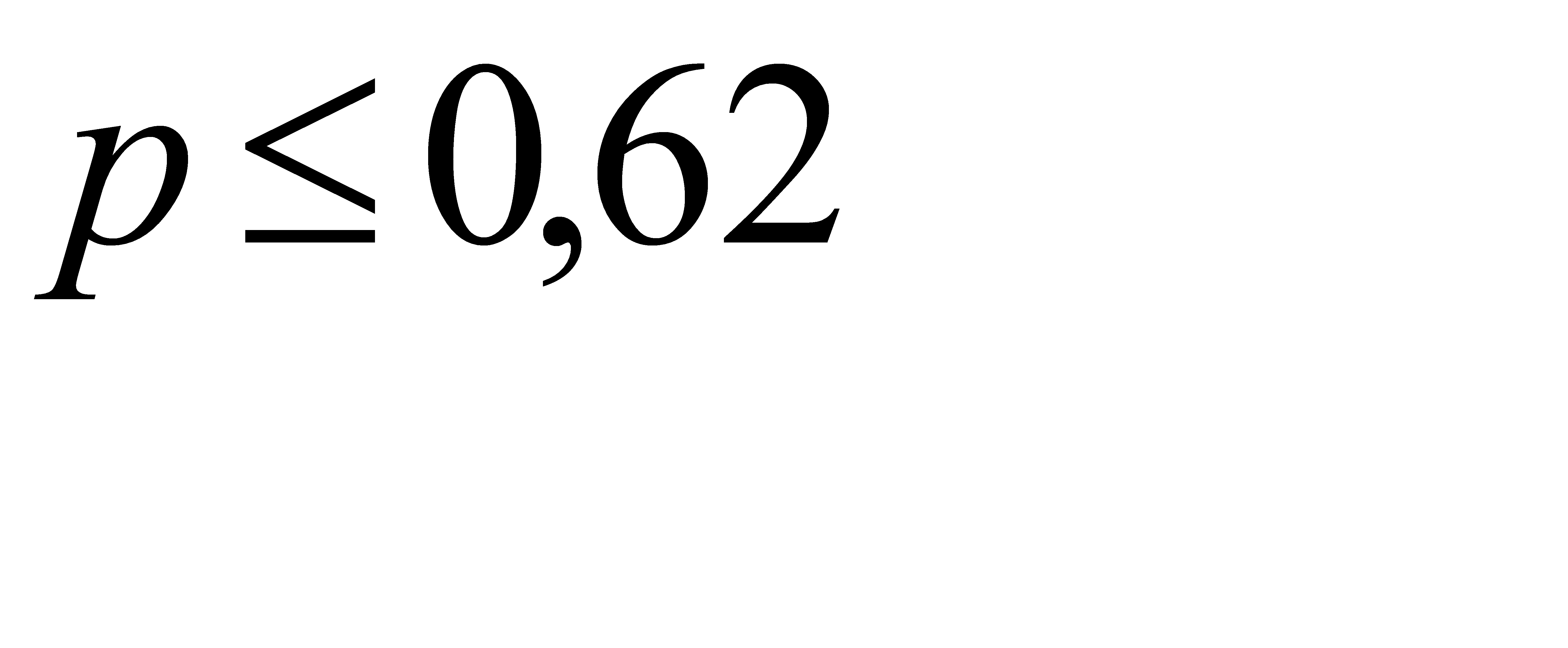 .
.
#156По условию n = 39, 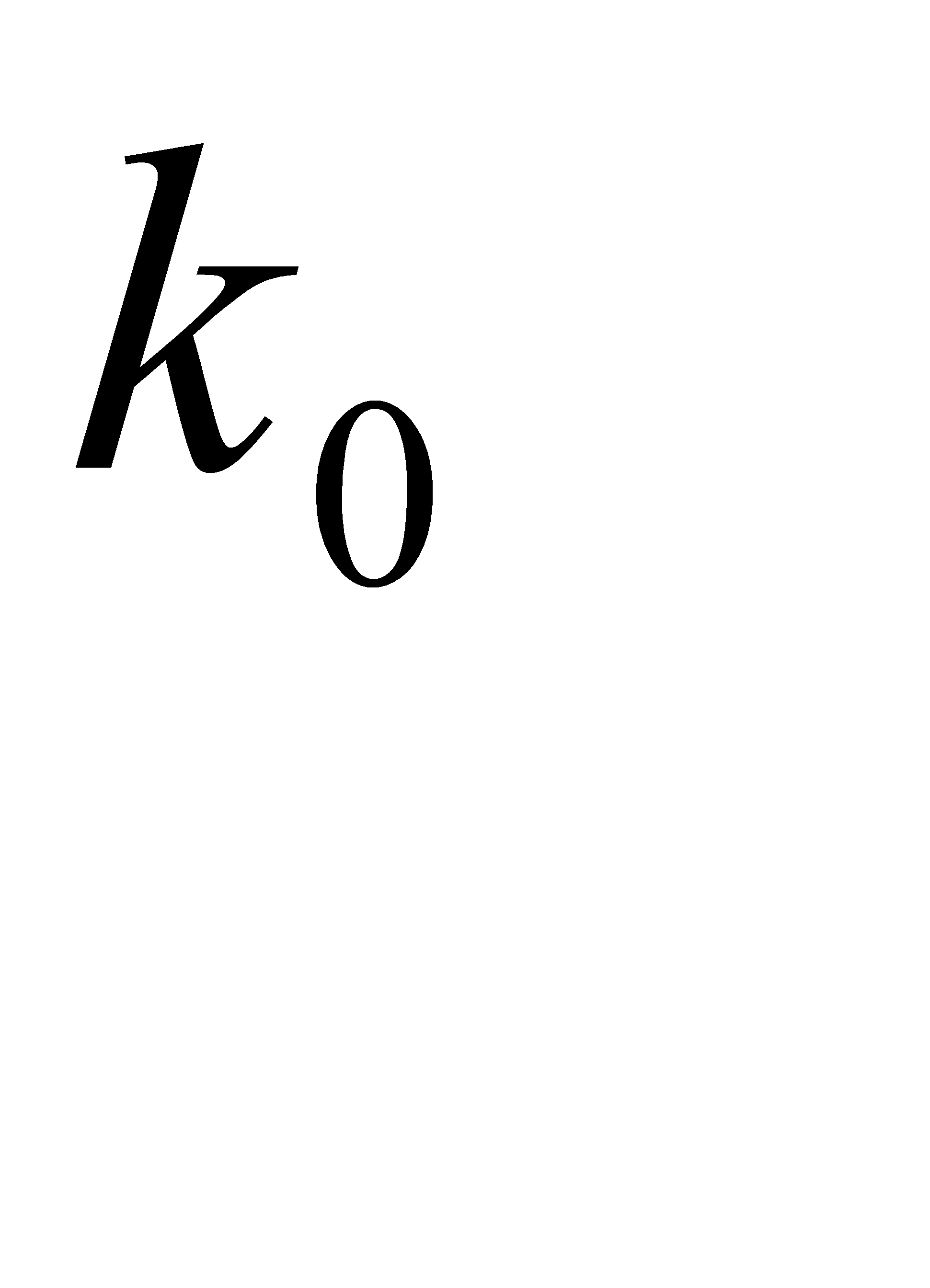 =25. Воспользуемся двойным неравенством
=25. Воспользуемся двойным неравенством  . Подставляя данные задачи, получим систему неравенств для определения неизвестной вероятности р:
. Подставляя данные задачи, получим систему неравенств для определения неизвестной вероятности р: 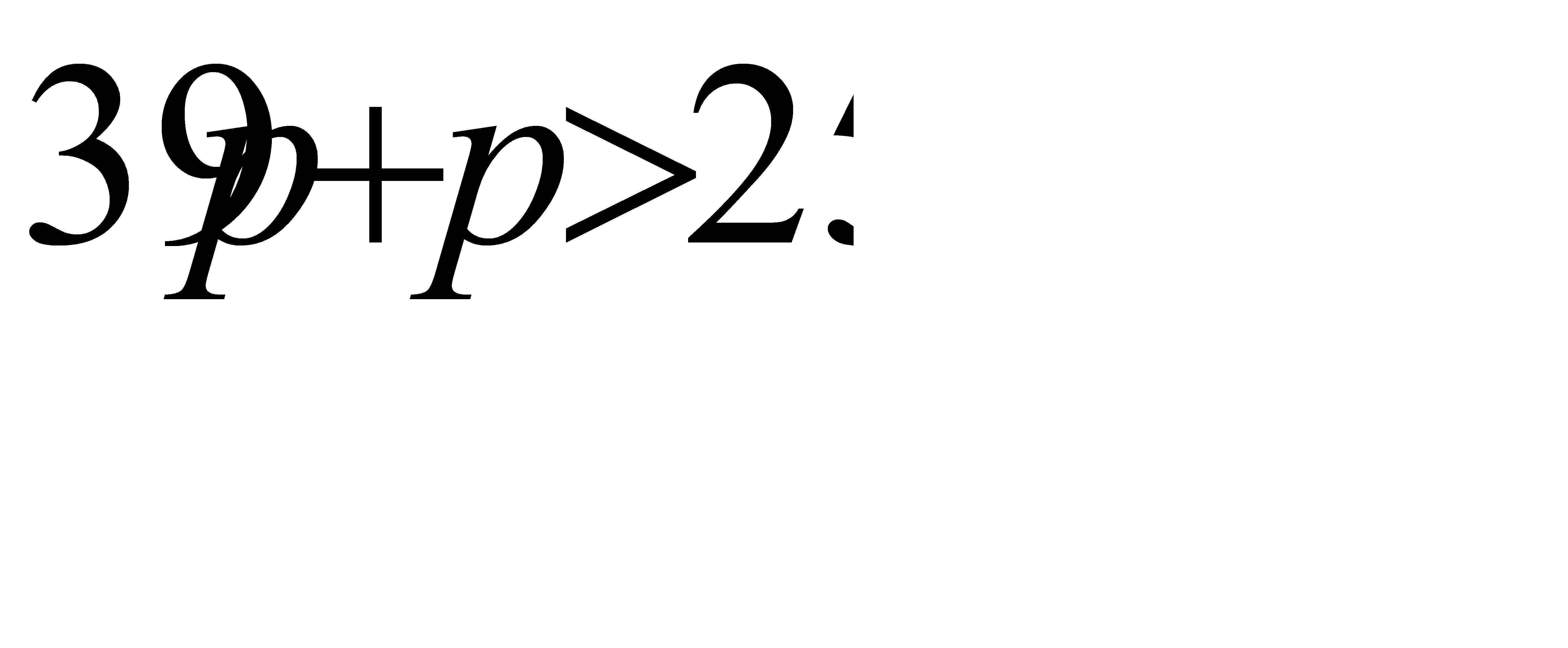 ,
, 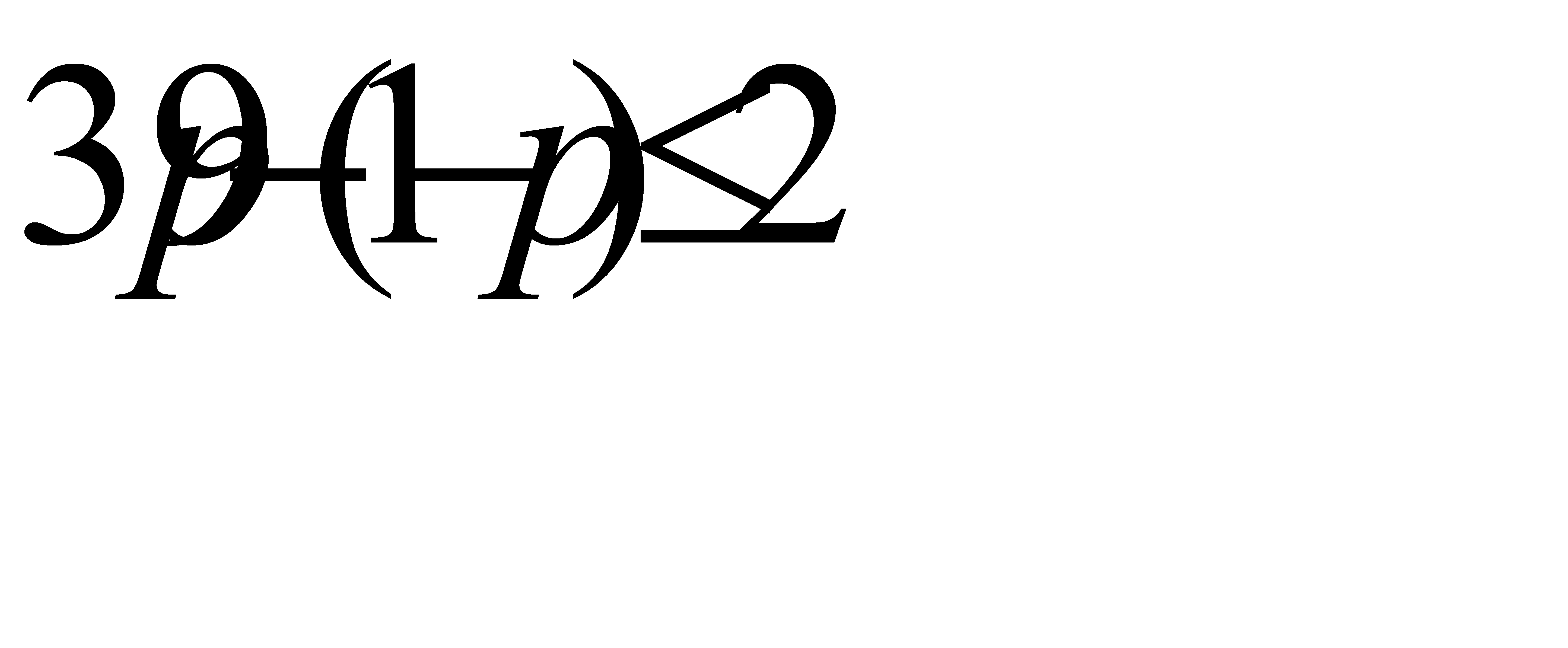
Из первого неравенства системы найдём p> 0, 625, из второго неравенства системы найдём 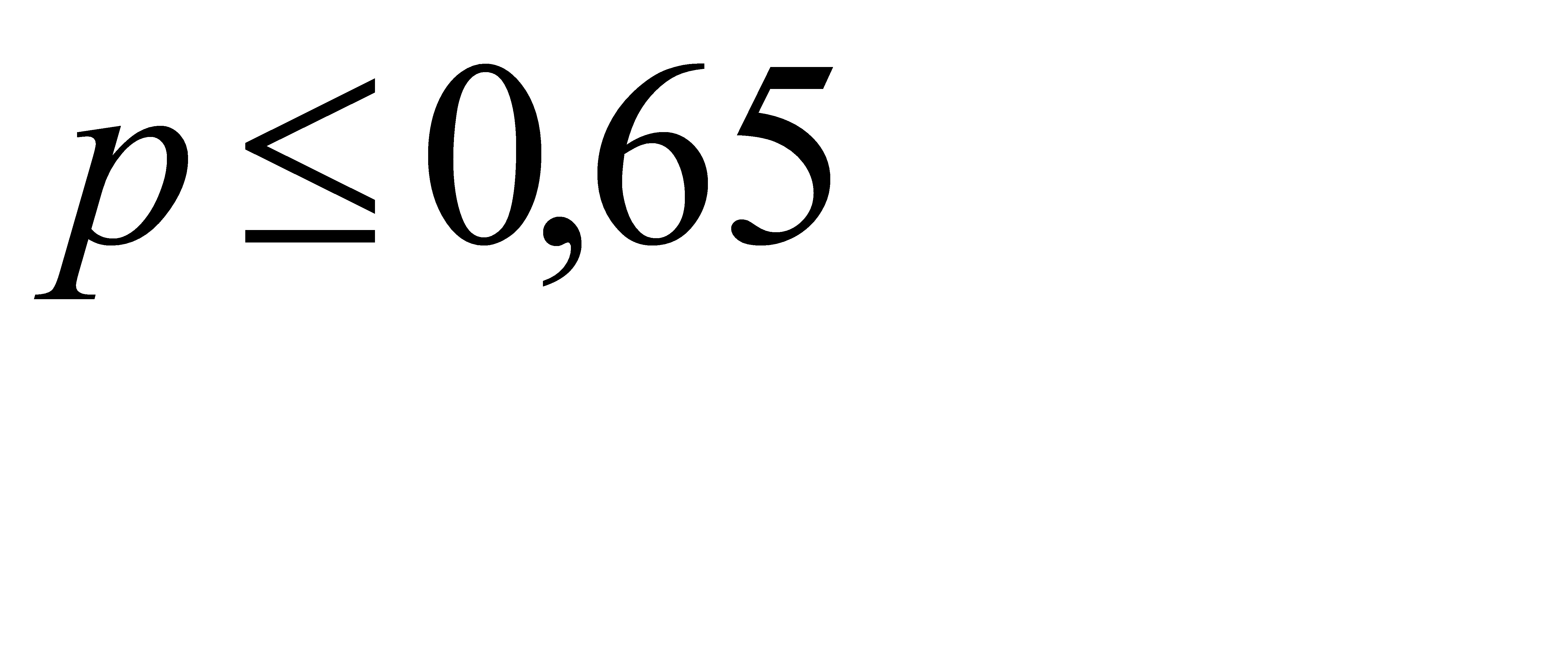 .
.
Итак, искомая вероятность должна удовлетворять двойному неравенству 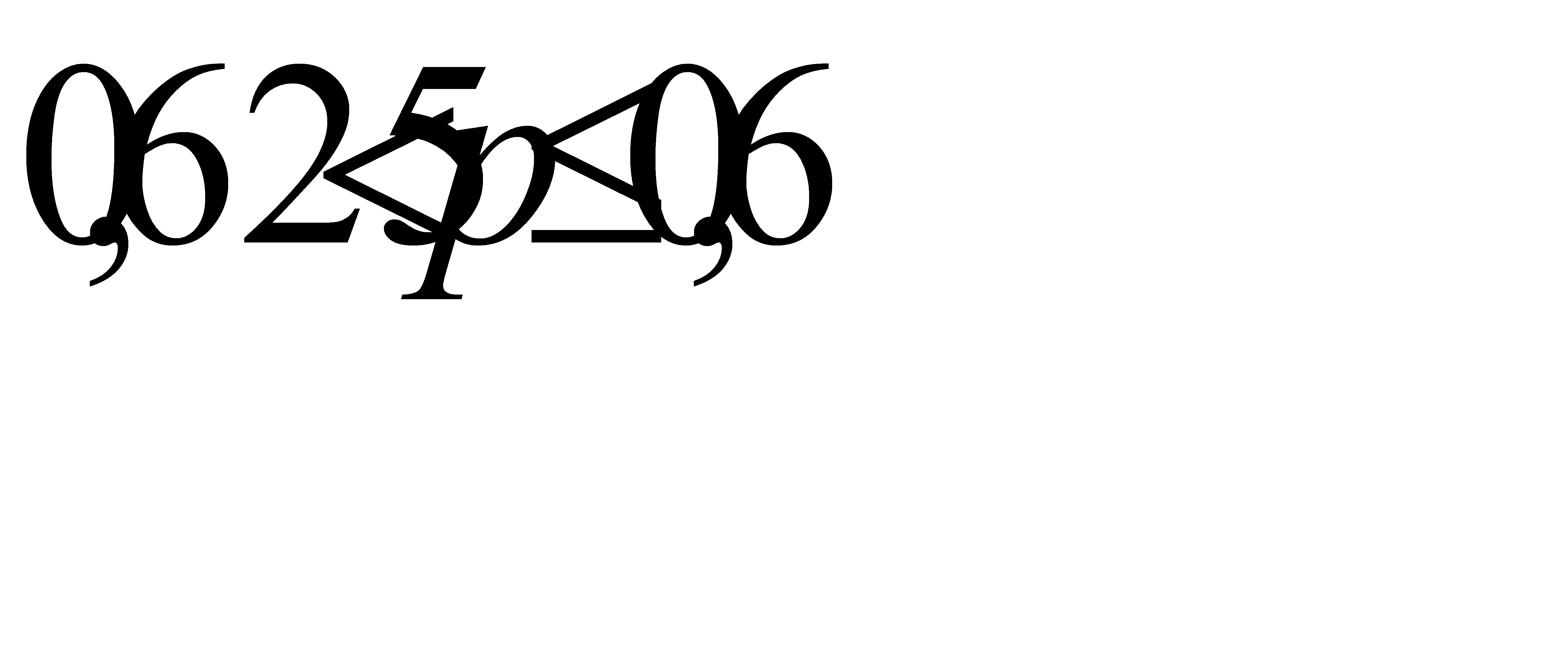 . Ответ:
. Ответ: 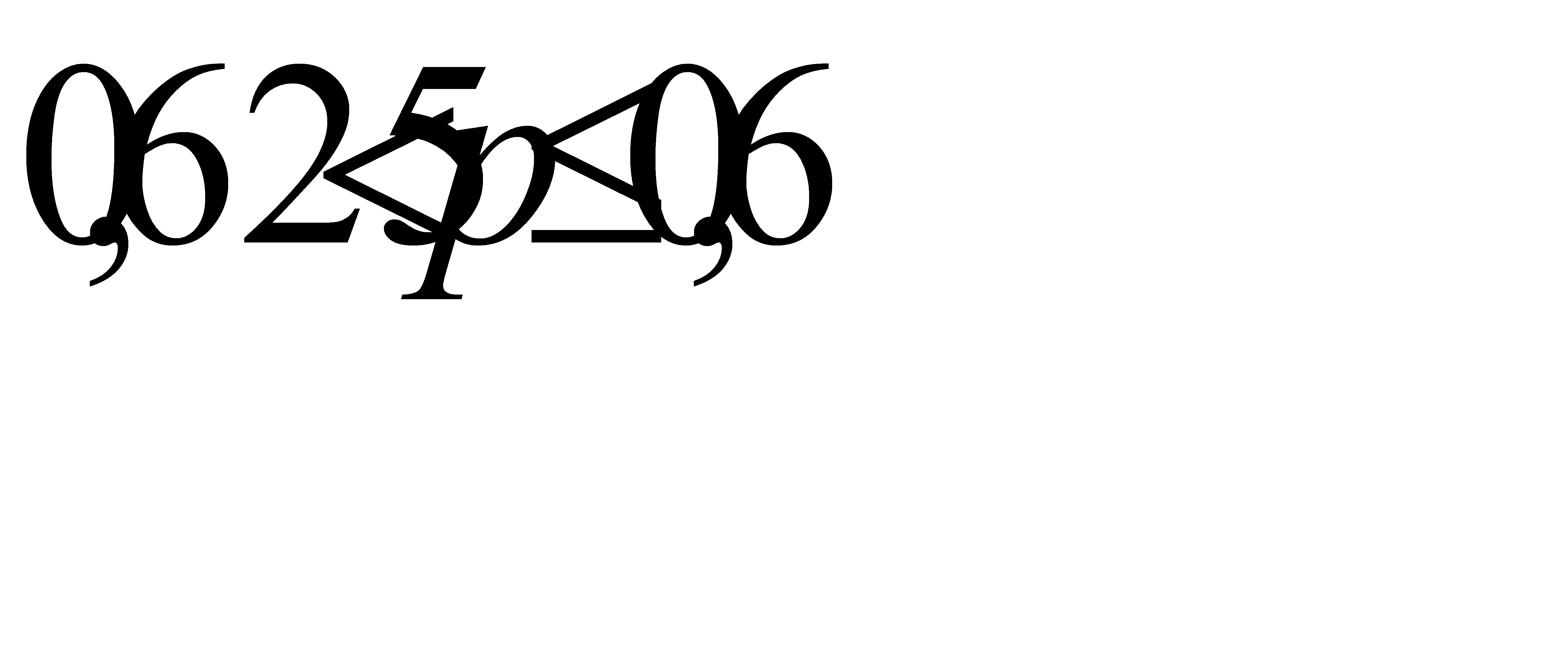
#157По условию, n=6; р=0, 3; q=0, 7. а) Найдем наивероятнейшее число попаданий по формуле
np—q 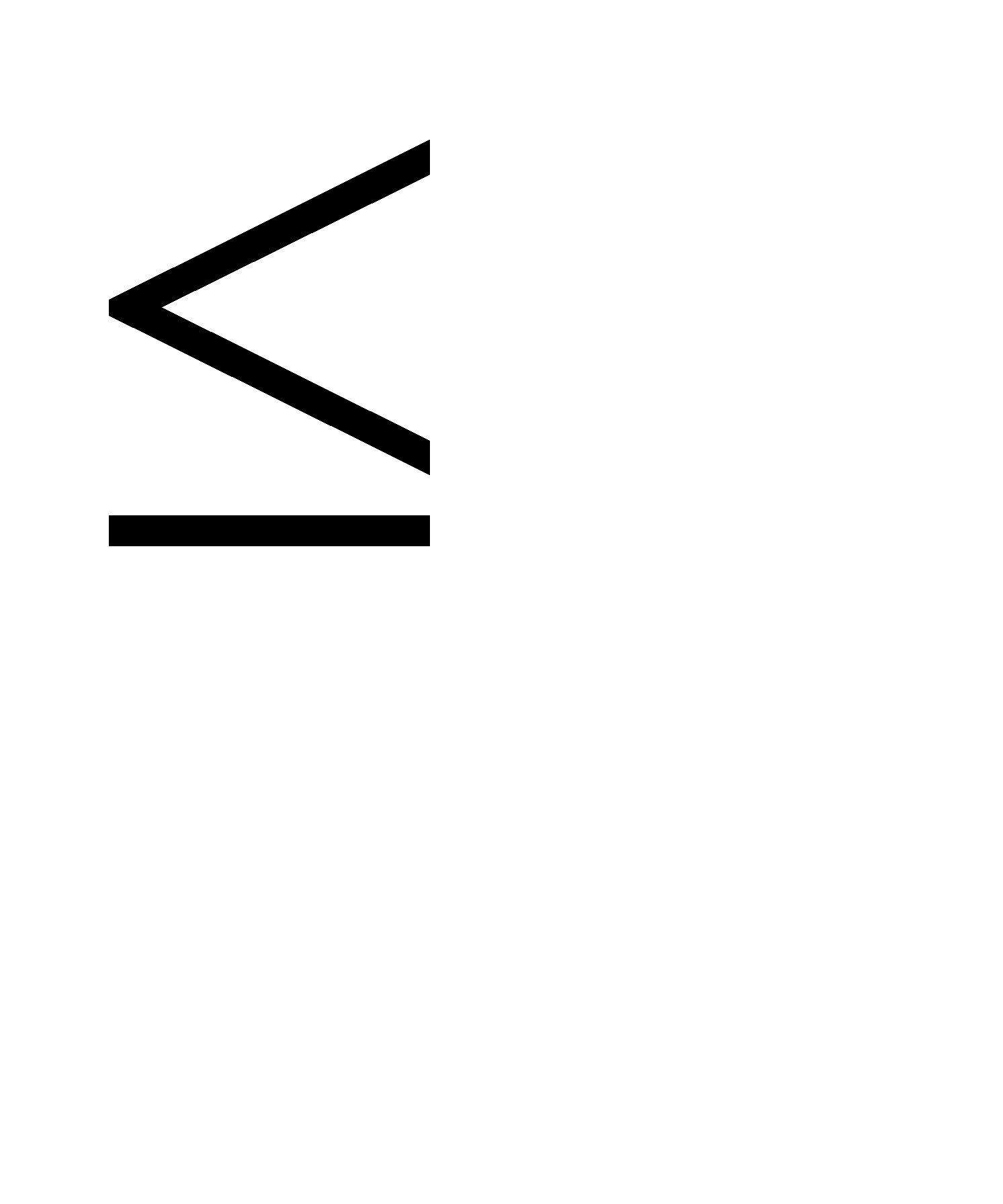 k
k 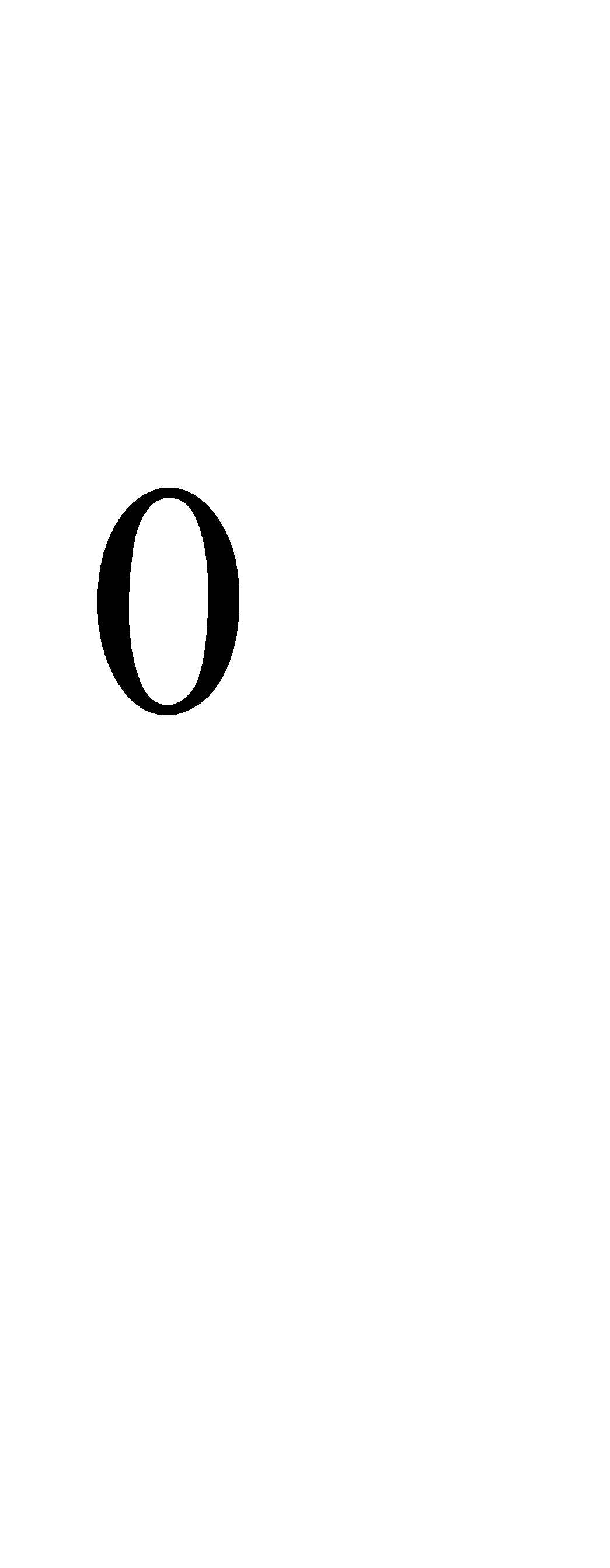 < nр + р. Подставив данные задачи, получим 6*0, 3—0, 7
< nр + р. Подставив данные задачи, получим 6*0, 3—0, 7  k
k 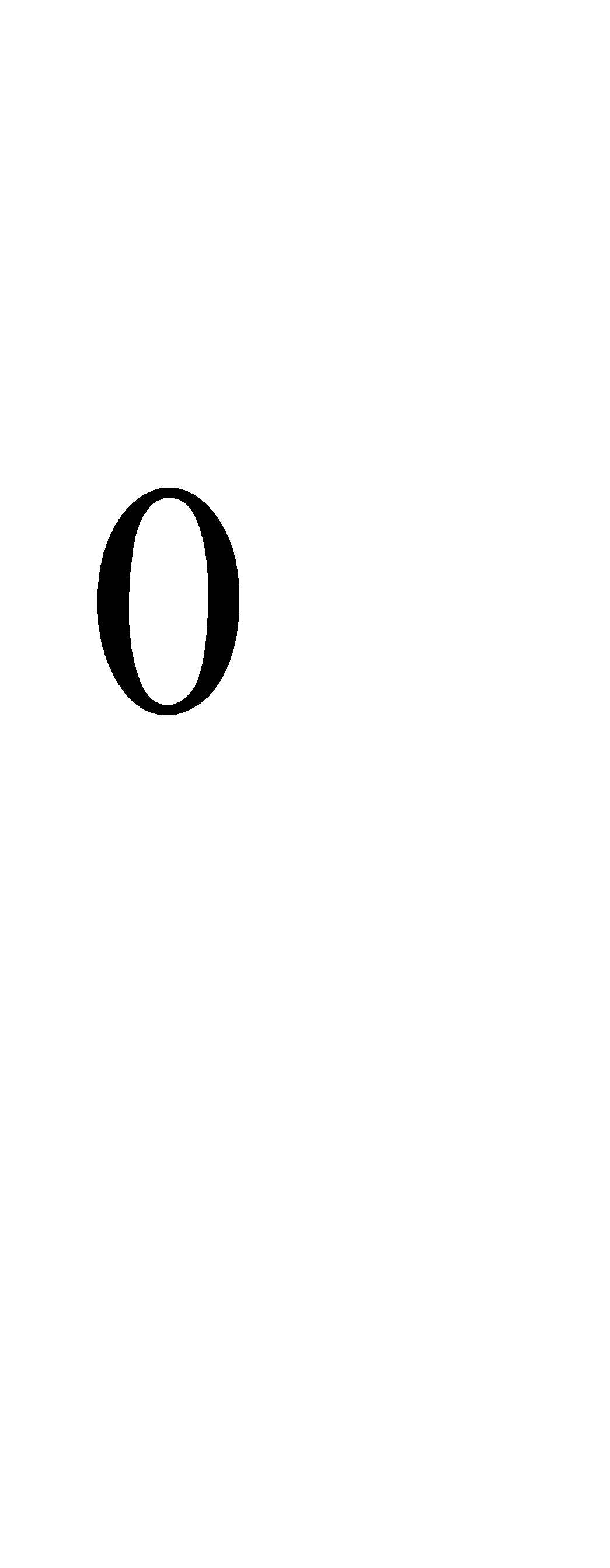 < 6*0, 3 + 0, 3 или 1, 1< k
< 6*0, 3 + 0, 3 или 1, 1< k 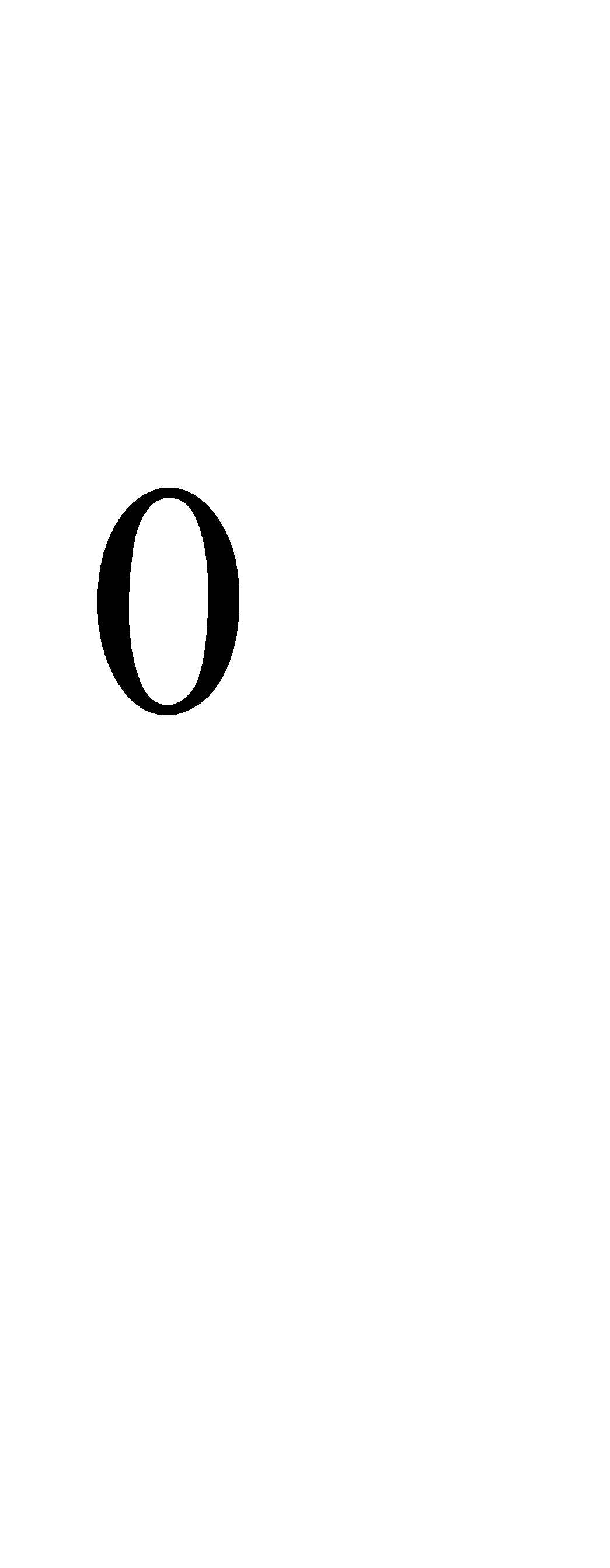 < 2, 1. Отсюда k
< 2, 1. Отсюда k 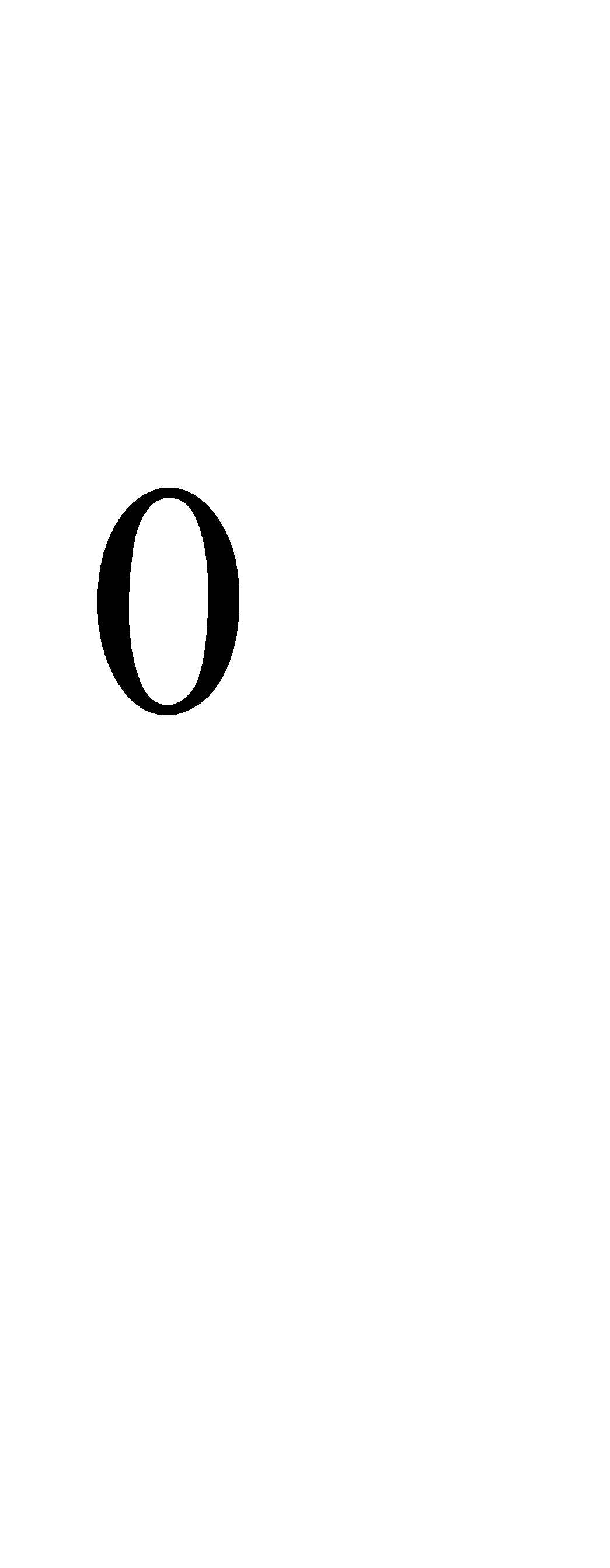 =2.
=2.
б) Найдем вероятность наивероятнеишего числа попаданий по формуле Бернулли 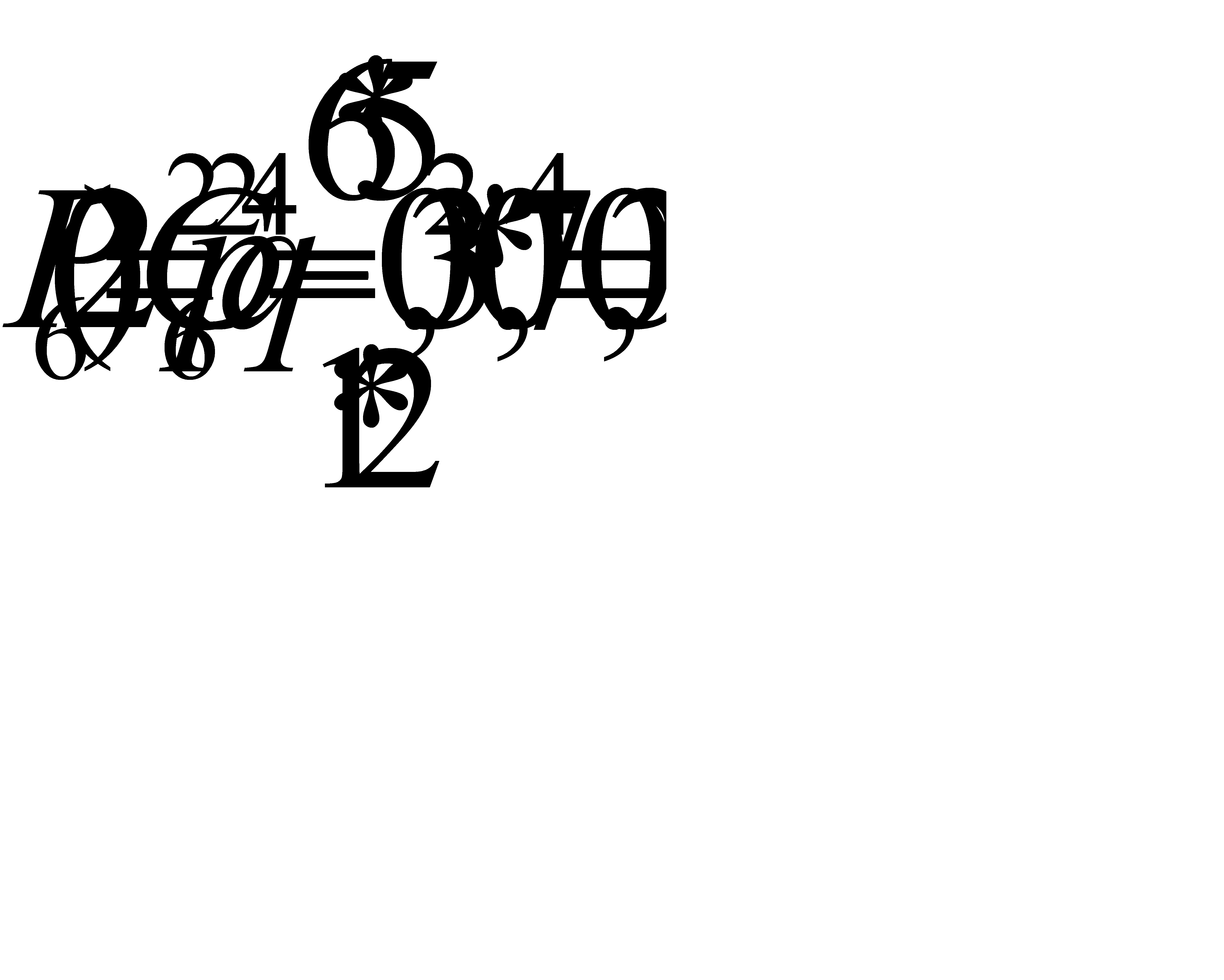
в) Найдем вероятность того, что объект будет разрушен. По условию, для этого достаточно, чтобы было или 2, или 3, или 4, или 5, или 6 попаданий. Эти события несовместны, поэтому вероятность разрушения объекта равна сумме вероятностей этих событий:

Однако проще сначала найти вероятность Q противоположного события (ни одного попадания или одно попадание):

Искомая вероятность того, что объект будет разрушен, P=l—Q=l—0, 42=0, 58. Ответ: а)2, б)0, 324, в)0, 58
#158По условию, n= 5; p= 0, 2; q= 0, 8; а) Найдем наивероятнейшее число отказов по формуле  . Подставив данные задачи, получим:
. Подставив данные задачи, получим: 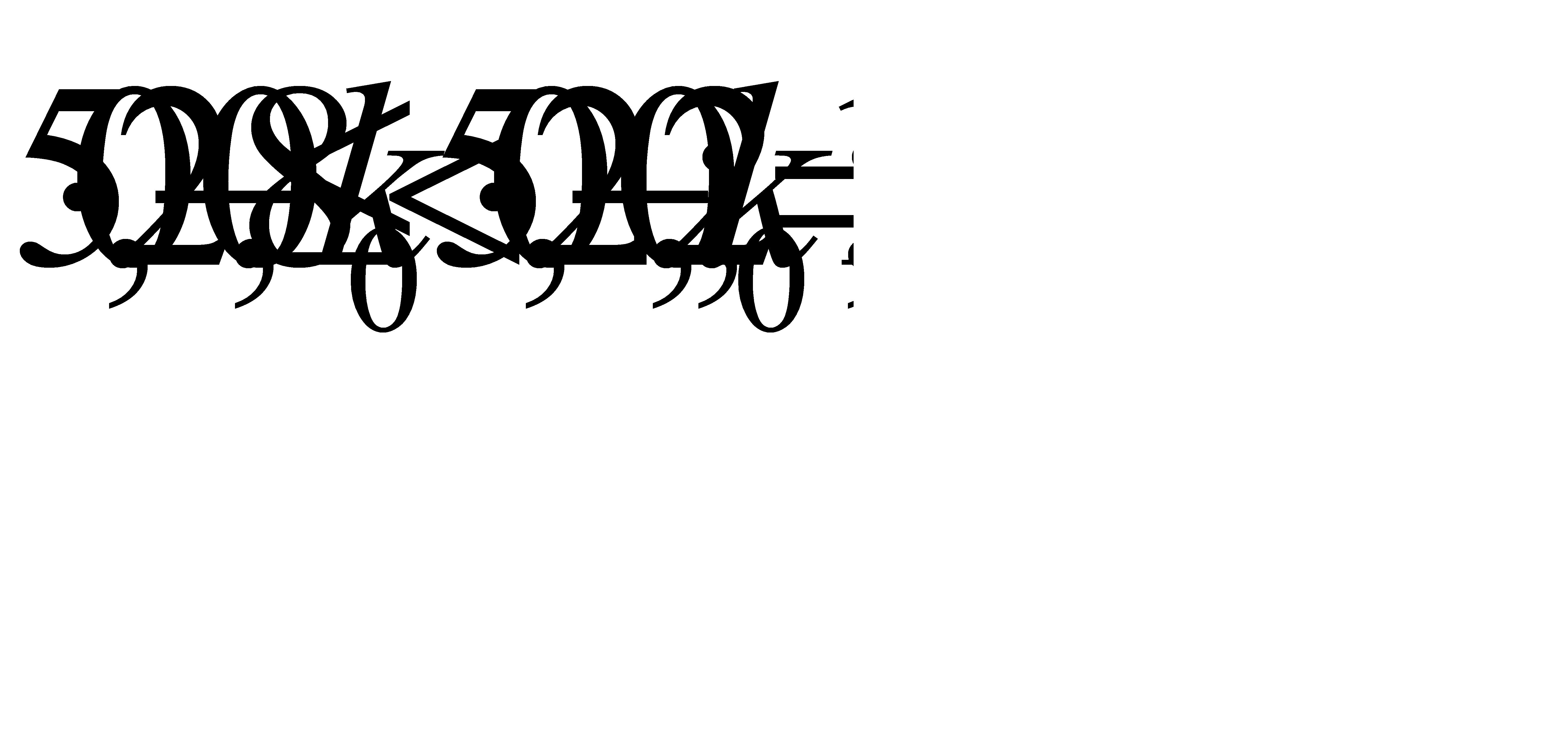 .
.
б) Найдем вероятность наивероятнейшего числа отказов по формуле Бернулли 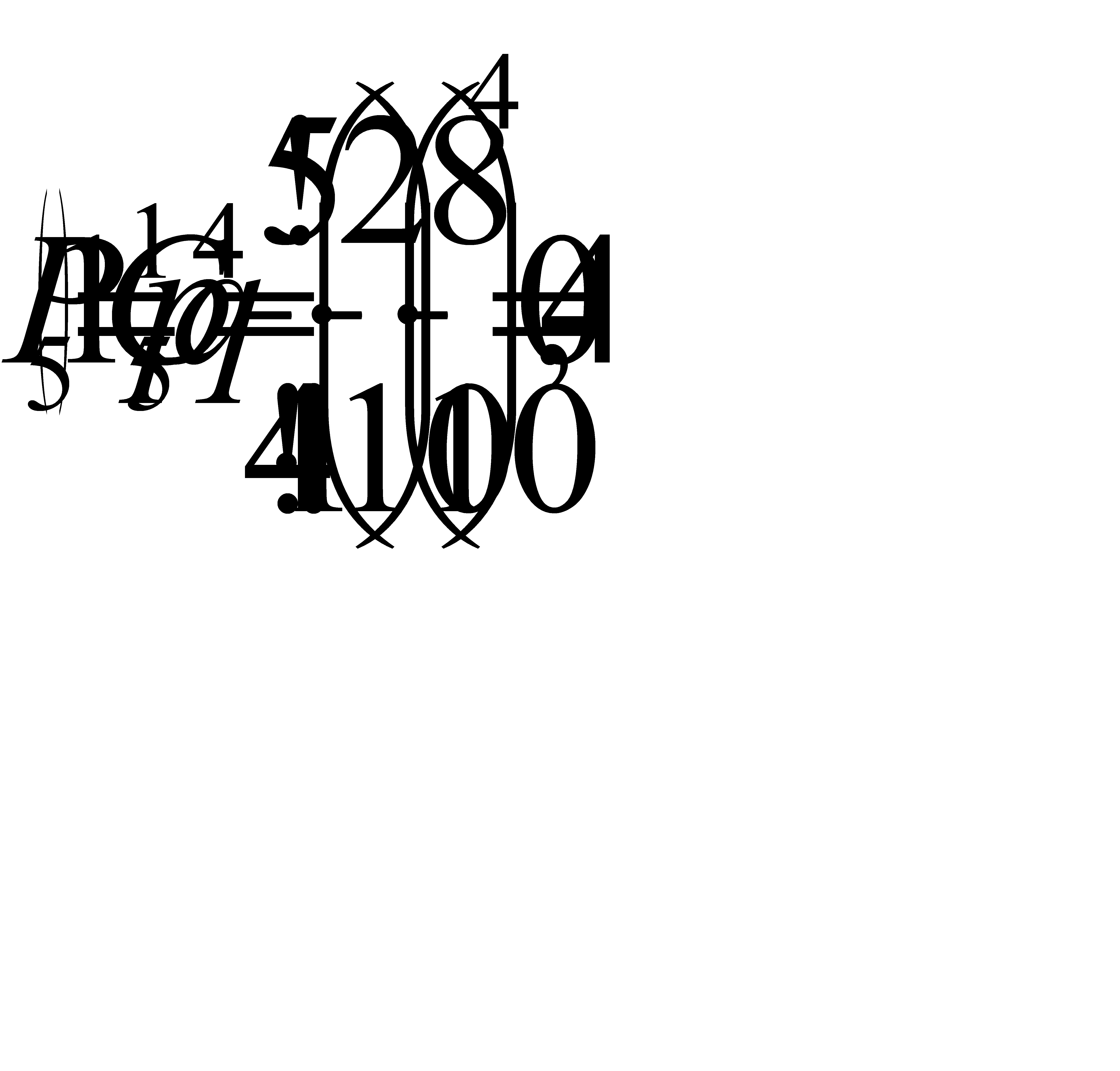
в) Найдем вероятность отказа прибора. Для того чтобы прибор был разрушен по условию задачи достаточно чтобы отказали 4 или 5 элементов.

#159 Вероятности безотказной работы элементов соответственно равны:
р1 = 0, 7, р2 = 0, 8, р3 = 0, 9, поэтому вероятности того, что элементы откажут, q1 = 0, 3; q2 = 0, 2; q3=0, 1.
Составим производящую функцию: φ 3(z) = (p1∙ z + q1) (p2∙ z + q2) (p3∙ z + q3) = (0, 7z + 0, 3)(0, 8z + 0, 2)(0, 9z + 0, 1) = 0, 504z3 + 0, 398z2 + 0, 092z + 0, 006.
а) Вероятность того, что три элемента будут работать безотказно, равна коэффициенту при z3: Р3(3) = 0, 504.
б) Вероятность того, что два элемента будут работать безотказно, равна коэффициенту при z2: Р3(2) = 0, 398.
в) Вероятность того, что один элемент будет работать безотказно, равна коэффициенту при z1: Р3(1) = 0, 092.
г) Вероятность того, что ни один из элементов не будет работать безотказно, равна свободному члену: Р3(0) = 0, 006.
Контроль: 0, 504 + 0, 398 + 0, 092 + 0, 006 = 1.
#161Вероятности попаданий соответственно равны ;
;
, поэтому вероятности того, орудия промахнутся,
;
. составим производящую функцию:
а) Вероятность того, что все три орудия попадут в цель равна коэффициенту при :
.
б) Вероятность того, что два орудия попадут в цель равна коэффициенту при :
.
в) Вероятность того, только одно орудие попадет в цель равна коэффициенту при :
.
г) Вероятность того, что ни одно орудие не попадет в цель равна свободному члену: .
д) Вероятность того, что хотя бы одно орудие попадет в цель равна: .
#162 Вероятности того, что элементы откажут равны
, поэтому вероятности безотказной работы,
. Составим производящую функцию:
а) Вероятность того, что все четыре элемента откажут равна коэффициенту при :
.
б) Вероятность того, что три элемента откажут равна коэффициенту при :
.
в) Вероятность того, два элемента откажут равна коэффициенту при :
.
г) Вероятность того, только один элемент откажет равна коэффициенту при :
г) Вероятность того, что ни один элемент не откажет равна свободному члену: .
д) Вероятность того, что не более двух элементов откажет равна: .
#163 Из условия задачи следует, что необходимо попадание хотя бы четырех орудий. То есть либо трех из одной + одно из другой.. составим производящую функцию для первой батареи:
а) Вероятность того, что все три орудия попадут в цель равна коэффициенту при :
.
б) Вероятность того, что два орудия попадут в цель равна коэффициенту при :
.
Вероятность того, что в цель попадет как минимум 2 снаряда равна:
Составим производящую функцию для второй батареи:
а) Вероятность того, что все три орудия попадут в цель равна коэффициенту при :
.
б) Вероятность того, что два орудия попадут в цель равна коэффициенту при :
.
Вероятность того, что в цель попадет как минимум 2 снаряда равна:
Таким образом вероятность уничтожения цели равна
#164Дискретная случайная величина Х задана законом распределения:
Х 1 3 6 8
Р 0, 2 0, 1 0, 4 0, 3
Построить многоугольник распределения.
Решение:
Построим прямоугольную систему координат, причем по оси абсцисс будем откладывать возможные значения xi, а по оси ординат- соответствующие вероятность pi. Построим точки 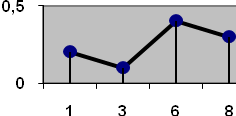
Полученный многоугольник и есть искомый многоугольник распределения.
#165 Дискретная случайная величина X задана законом распределения:
а) X 2 4 5 6 ) X 10 15 20
р 0, 3 0, 1 0, 2 0, 4 р 0, 1 0, 7 0, 2
Построить многоугольник распределения.
Решение. Построим прямоугольную систему координат, при-
причем по оси абсцисс будем откладывать возможные значения х; а по
оси ординат — соответствующие вероятности р.
Построим точки: а)А(2; 0, 3), В(4; 0, l), С(5; 0, 2) и D(6; 0, 4). Соединив эти точки
отрезками прямых, получим искомый многоугольник распределения.
б)А(10; 0, 1), В(15; 0, 7), С(20; 0, 2). Соединив эти точки
отрезками прямых, получим искомый многоугольник распределения.
#166 дискретная случайная величина Х (число отказавших элементов в одном опыте) имеет следующие возможные значения: 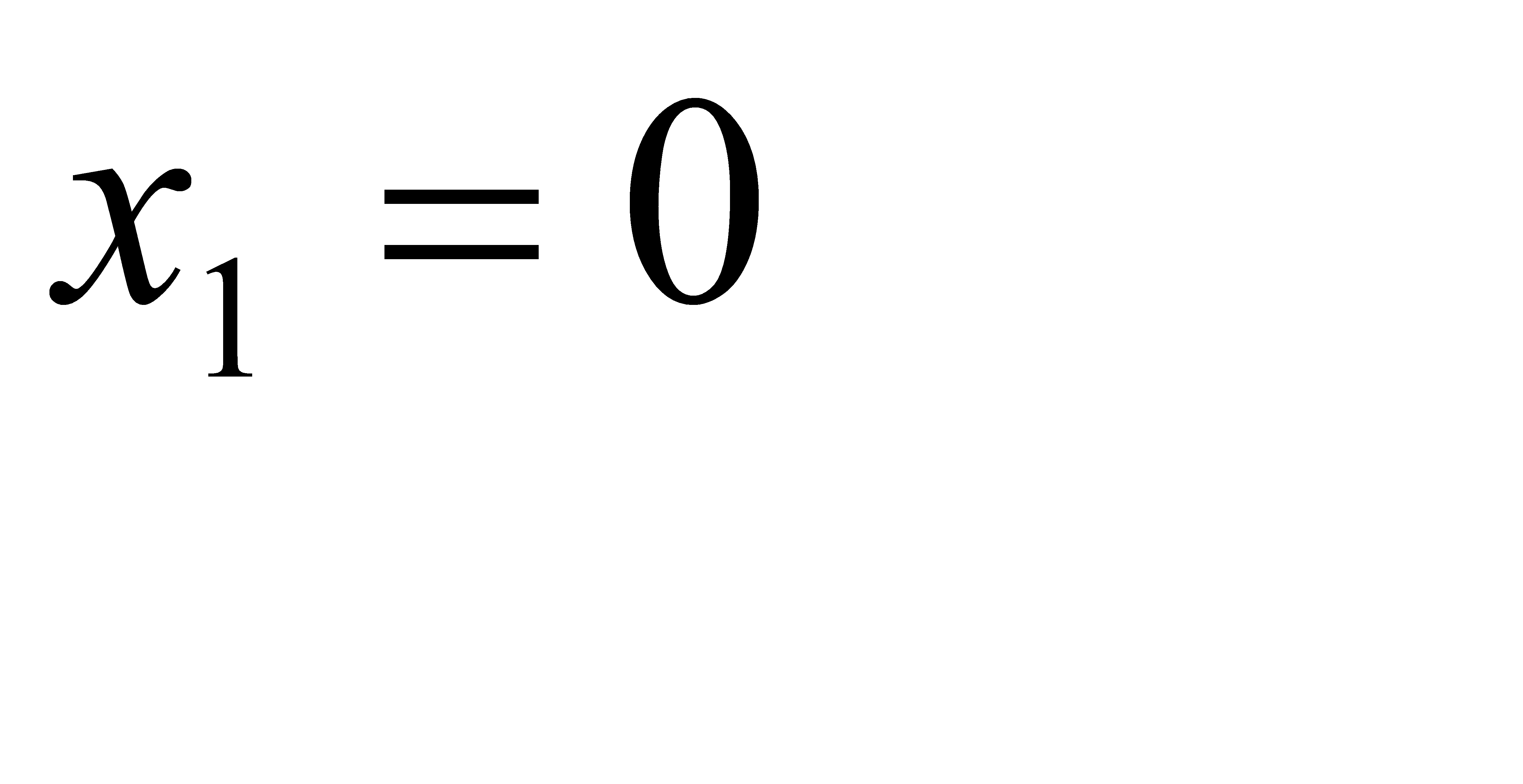 (ни один из элементов устройства не отказал),
(ни один из элементов устройства не отказал), 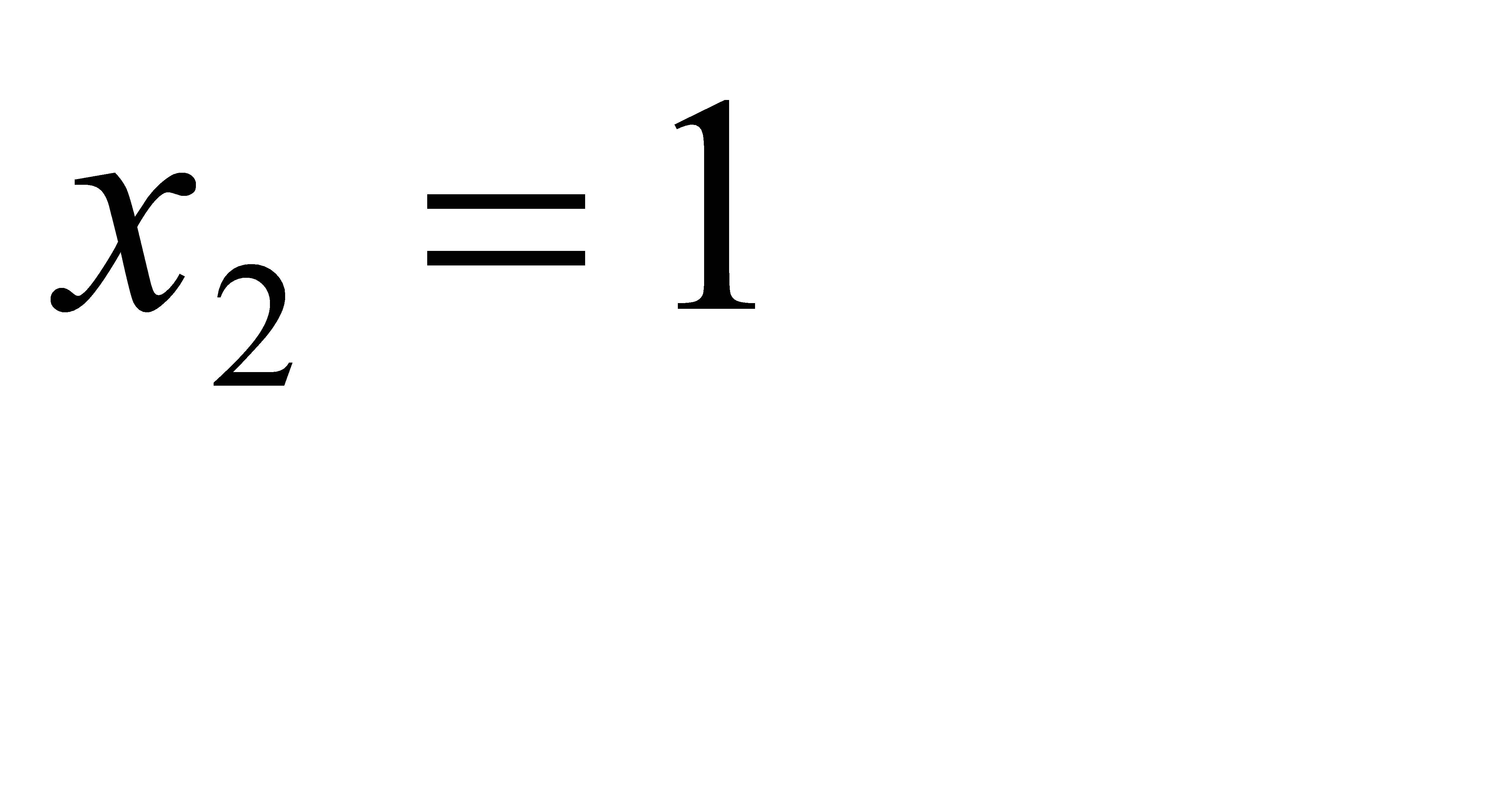 (отказал один элемент),
(отказал один элемент), 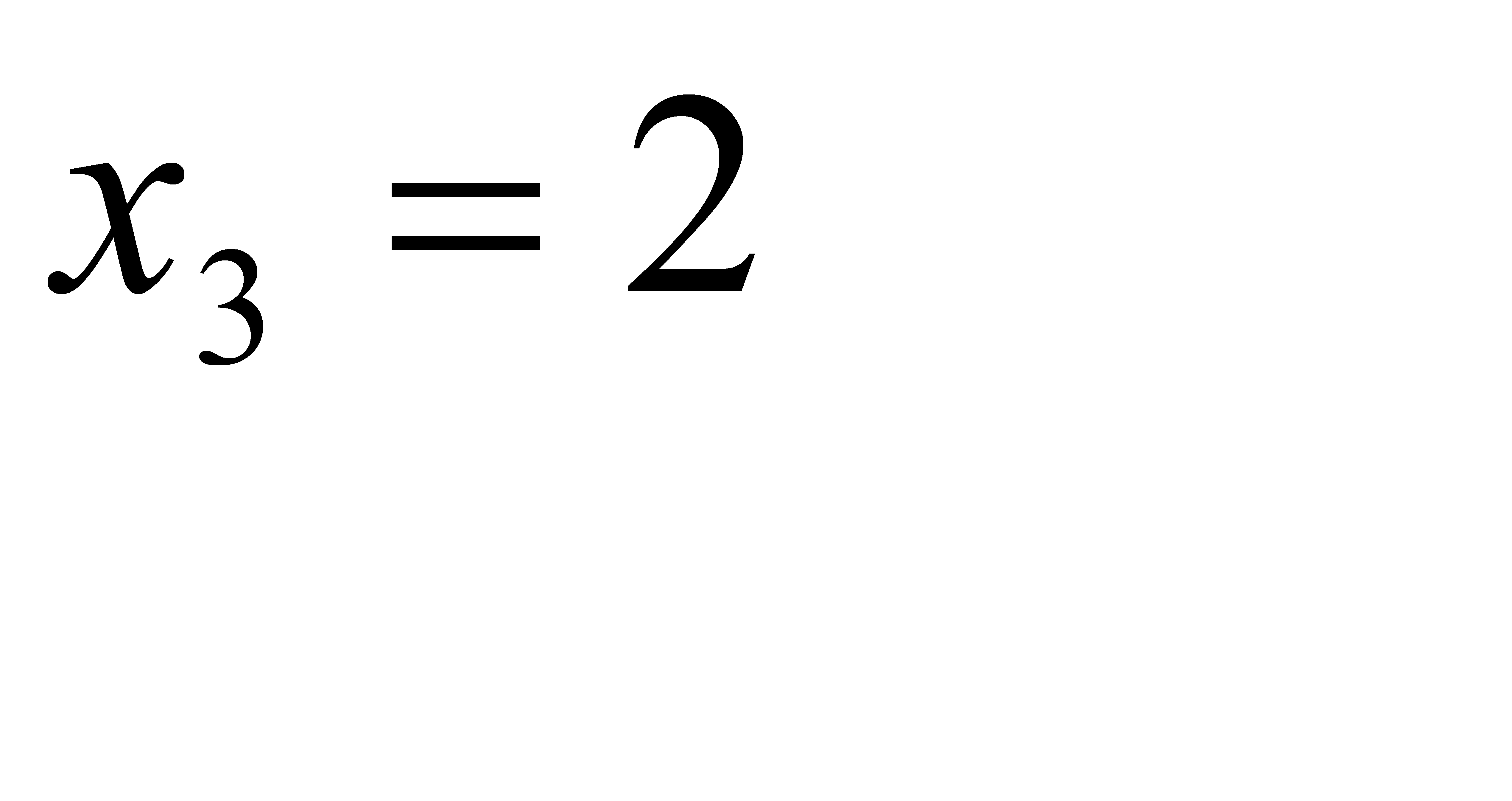 (отказали 2 элемента) и
(отказали 2 элемента) и 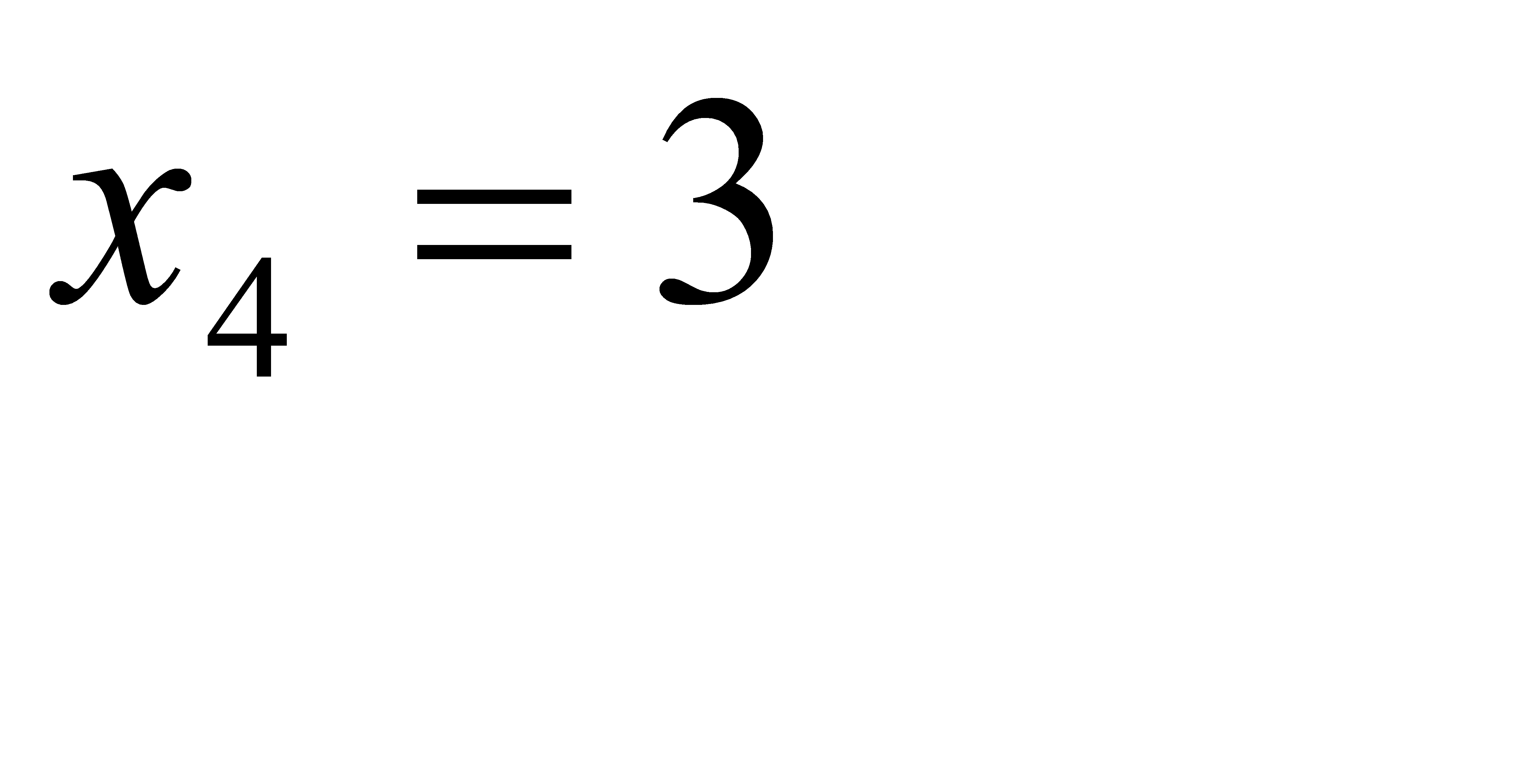 (отказали 3 элемента). Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что по условию n = 3, p = 0, 1 (следовательно q = 0, 9), получим:
(отказали 3 элемента). Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что по условию n = 3, p = 0, 1 (следовательно q = 0, 9), получим: 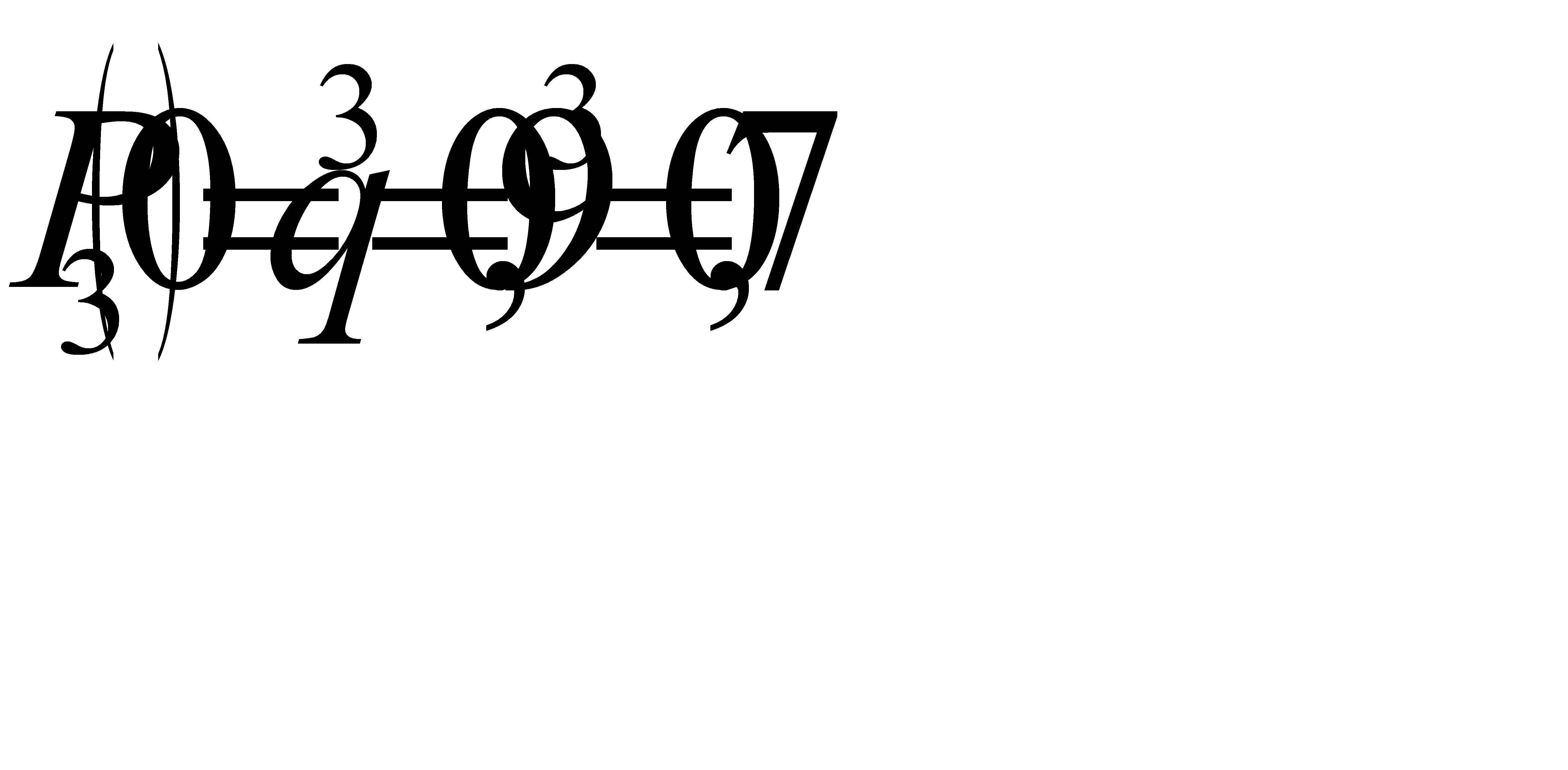 ;
; 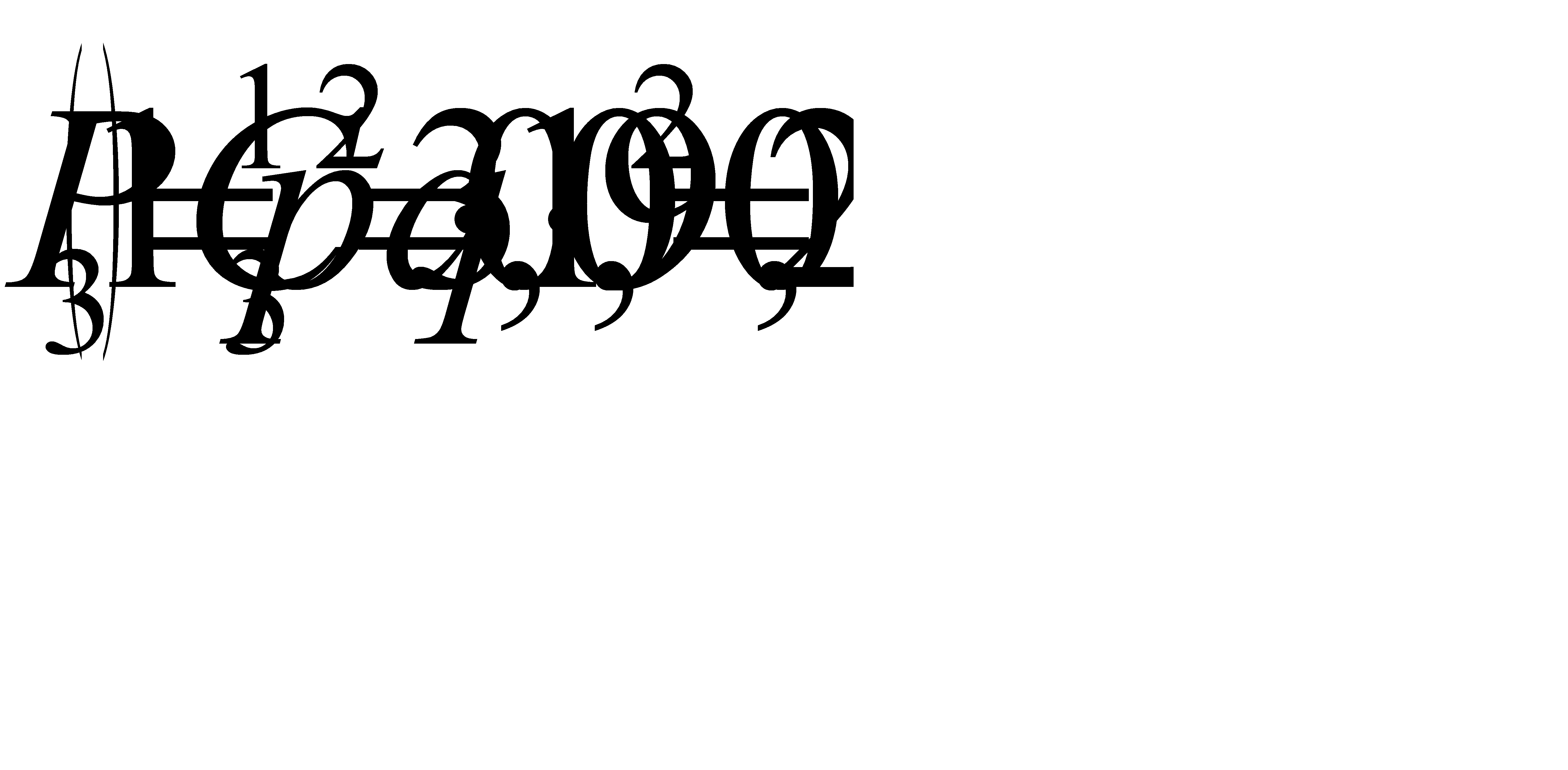 ;
;
 ;
; 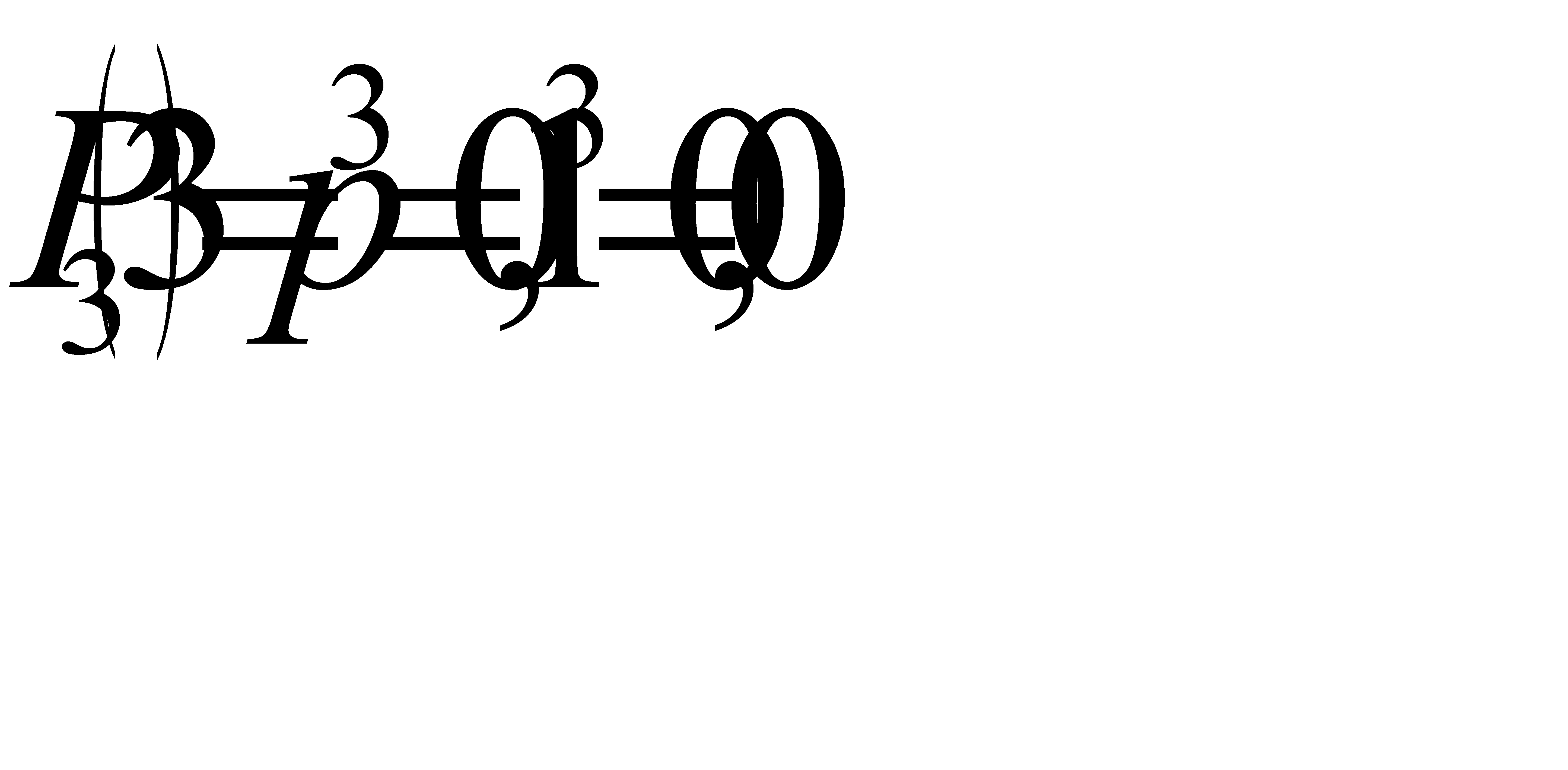 .
.
Проверим:  .
.
Напишем искомый биномиальный закон распределения Х:
X 0 1 2 3
p 0, 729 0, 243 0, 027 0, 001
#167дискретная случайная величина 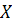 (число нестандартных деталей среди 4 отобранных) имеет следующие возможные значения:
(число нестандартных деталей среди 4 отобранных) имеет следующие возможные значения: 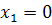 (отобрали только стандартные детали),
(отобрали только стандартные детали), 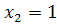 (отобрали одну нестандартную и три стандартных),
(отобрали одну нестандартную и три стандартных), 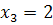 (отобрали две нестандартных и две стандартных),
(отобрали две нестандартных и две стандартных), 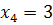 (отобрали три нестандартных и одну стандартную),
(отобрали три нестандартных и одну стандартную), 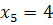 (отобрали только нестандартные). Вероятность отобрать из партии нестандартную деталь
(отобрали только нестандартные). Вероятность отобрать из партии нестандартную деталь 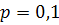 . По условию
. По условию 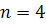 . Найдём
. Найдём 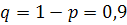 . Получим:
. Получим:
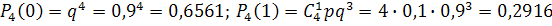
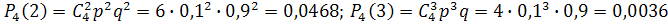
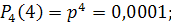
| Возможные значения | |||||
| Вероятности | 0, 6561 | 0, 2916 | 0, 0486 | 0, 0036 | 0. 0001 |
Напишем искомый биномиальный закон 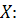
Построим многоугольник распределения дискретной случайной величины 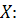

#168Написать биноминальный закон распределения дискретной случайной величины X –числа появлений «герба» при двух бросаниях монеты.
РЕШ-Е: Дискретная случайная величина 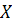 (число появлений «герба» при двух бросаниях монеты) имеет следующие возможные значения: («герб» ни разу не выпал), («герб» выпал только при одном броске), («герб» выпадал при каждом броске).
(число появлений «герба» при двух бросаниях монеты) имеет следующие возможные значения: («герб» ни разу не выпал), («герб» выпал только при одном броске), («герб» выпадал при каждом броске).
Очевидно что искомый биномиальный закон будет выглядеть следующим образом:
| Возможные значения | |||
| Вероятности | 1/4 | 1/2 | 1/4 |
#169
Всего вариантов выпадений: 6*6=36.
Четных 3 грани на каждом кубике => 3*3=9 – четное число очков на каждой игральной кости.
p=9/36=1/4 – вероятность выпадения четного числа очков на каждой игральной кости.
q=1-p=3/4Pn(k)=Cnk*pk*qn-k
Pn(0)=9/16 Pn(1)=6/16 Pn(0)=1/16
X 0 1 2
P 9/16 6/16 1/16
#170 Случайная величина X—число стандартных деталей среди отобранных деталей—имеет следующие возможные значения: X1=0; X2=1; X3=2; Найдем вероятности возможных значений X по Формуле: PX=k= Cnk*CN-nm-kCNm.
(N—число деталей в партии, n— число стандартных деталей в партии, m— число отобранных деталей, k— число стандартных деталей среди отобранных), находим: PX=0=C80*C22C102=145; PX=1=C81*C21C102=1645;
PX=2=C82*C20C102=2845; Составим искомый закон распределения:
| X | |||
| P | 1/45 | 16/45 | 28/45 |
Контроль: 145+1645+2845=1.
#171Случайная величина Х имеет следующие возможные значения х1=1, х2=2, х3=3.
Найдем вероятности возможных значений Х. Р(Х=1)=С41 С22 /С63=1/5, Р(Х=2)=С42 С21 /С63=3/5
Р(Х=3)=С43 С20 /С63=1/5
Составим искомый закон распределения:
Х 0 1 2 3
Р 0 1/5 3/5 1/5
#172 а) Дискретная случайная величина Х – число заданных вопросов – имеет следующие возможные значения: x1=1, x2=2, x3=3, …, xk=k, … Найдем вероятности этих возможных значений.
Величина Х примет возможное значение x1=1 (экзаменатор задаст только один вопрос), если студент не ответит на первый вопрос. Вероятность этого возможного значения равна 1-0, 9=0, 1. Таким образом, P(X=1)=0, 1.
Величина Х примет возможное значение x2=2 (экзаменатор задаст только два вопроса), если студент ответит на первый вопрос и не ответит на второй. Таким образом, P(X=2)=0, 9*0, 1=0, 09.
Аналогично найдем P(X=3)=0, 9*0, 9*0, 1=0, 081, …, 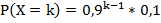
Выпишем искомый закон распределения:
| X | … | k | … | |||
| p | 0, 1 | 0, 09 | 0, 081 | … | 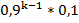
| … |
б) Наивероятнейшее число k0 заданных вопросов (наивероятнейшее возможное значение Х), т. е. число заданных преподавателем вопросов, которое имеет наибольшую вероятность, как следует из закона распределения, равно 1.
#173
Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0, 8. Стрелку выдаются патроны до тех пор, пока он не промахнется. Требуется: а) составить закон распределения дискретной случайной величины X—числа патронов, выданных стрелку; б) найти наивероятнейшее число выданных стрелку патронов.
Решение: а) Дискретная случайная величина Х – число выданных патронов – имеет следующие возможные значения: x1=1, x2=2, x3=3, …, xk=k, … Найдем вероятности этих возможных значений.
Величина Х примет возможное значение x1=1 (выдадут только один патрон), если не попадет при первом выстреле. Вероятность этого возможного значения равна 1-0, 8=0, 2. Таким образом, P(X=1)=0, 2.
Величина Х примет возможное значение x2=2 (выдадут два патрона), если попадет первый раз, но промахнется во второй. Таким образом, P(X=2)=0, 8*0, 1=0, 08.
Аналогично найдем P(X=3)=0, 8*0, 8*0, 2=0, 128, …, 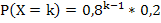
Выпишем искомый закон распределения:
| X | … | k | … | |||
| p | 0, 2 | 0, 08 | 0, 128 | … | 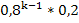
| … |
б) Наивероятнейшее число k0 выданных патронов (наивероятнейшее возможное значение Х), т. е. число выданных патронов, которое имеет наибольшую вероятность, как следует из закона распределения, равно 1.
Ответ: а) 0, 2, 0, 08, …, 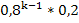 б) 1.
б) 1.
#174
Из двух орудий поочередно ведется стрельба по цели до первого попадания одним из орудий. Вероятность попадания в цель первым орудием равна 0, 3, вторым — 0, 7.
Начинает стрельбу первое орудие. Составить законы распределения дискретных случайных величин X и Y—числа израсходованных снарядов соответственно первым и вторым орудием.
Решение.
Пусть события 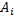 и
и 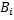 — попадание в цель соответственно первым и вторым орудием при i-м выстреле;
— попадание в цель соответственно первым и вторым орудием при i-м выстреле; 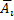 и
и 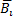 - промахи.
- промахи.
Найдем закон распределения случайной величины X—числа израсходованных первым орудием снарядов. Первое орудие израсходует один снаряд (Х=1), если оно попадет в цель при первом
выстреле, или оно промахнется, а второе орудие при первом выстреле попадет в цель:
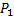 =P(X=1)=P(
=P(X=1)=P(  +
+ 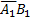 )=P(
)=P(  )+P(
)+P( 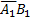 )= P(
)= P(  )+ P(
)+ P( 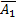 )* P(
)* P( 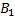 )=0, 3+0, 7*0, 7=0, 79.
)=0, 3+0, 7*0, 7=0, 79.
Первое орудие израсходует два снаряда, если оба орудия при первом выстреле промахнутся, а при втором выстреле первое орудие попадет в цель, или если оно промахнется, а второе орудие при втором выстреле попадет в цель:
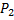 =P(X = 2)=Р(
=P(X = 2)=Р( 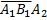 +
+ 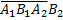 )=
)=
= 0, 7*0, 3*0, 3 + 0, 7*0, 3*0, 7*0, 7 = 0, 21 (0, 3 + 0, 49) = 0, 79*0, 21.
Аналогично получим
Р(Х=k)=0, 79* 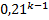 .
.
Искомый закон распределения дискретной случайной величины X— числа снарядов, израсходованных первым орудием:
| X | … | k | … | |||
| p | 0, 79 | 0, 79*0, 21 | 0, 79*0, 212 | … | 0, 79* 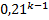
| … |
Контроль: 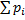 = 0, 79/(1-0, 21) =0, 79/0, 79=1.
= 0, 79/(1-0, 21) =0, 79/0, 79=1.
Найдем закон распределения дискретной случайной величины Y—числа снарядов, израсходованных вторым орудием. Если первое орудие при первом выстреле попадет в цель, то
стрельба из второго орудия не будет произведена:
p1=P(Y=0) = P (  ) =0, 3.
) =0, 3.
Второе орудие израсходует лишь один снаряд, если при первом выстреле оно попадет в цель, или если оно промахнется, а первое орудие попадет в цель при втором выстреле:
p2 = P(Y=l) = P( 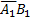 +
+ 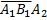 ) = 0, 7*0, 7 + 0, 7*0, 3*0, 3 = 0, 553.
) = 0, 7*0, 7 + 0, 7*0, 3*0, 3 = 0, 553.
Вероятность того, что второе орудие израсходует два снаряда,
Рз=Р(Y=2) = Р( 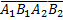 +
+ 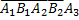 ).
).
Выполнив выкладки, найдем р3 = 0, 553*0, 21.
Аналогично получим
P(Y=k)=0, 553* 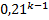 .
.
Искомый закон распределения дискретной случайной величины
Y — числа снарядов, израсходованных вторым орудием:
| Y | … | k | … | |||
| p | 0, 3 | 0, 553 | 0, 553*0, 21 | … | 0, 553* 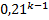
| … |
Контроль: 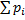 = 0, 3+ (0, 553/1 —0, 21)=0, 3+(0, 553/0, 79) =
= 0, 3+ (0, 553/1 —0, 21)=0, 3+(0, 553/0, 79) =
= 0, 3+0, 7=1.
#175
Два бомбардировщика поочередно сбрасывают бомбы на цель до первого попадания. Вероятность попадания в цель первым бомбардировщиком равна 0, 7, вторым — 0, 8. Вначале сбрасывает бомбы первый бомбардировщик. Составить первые четыре члена закона распределения дискретной случайной величины X—числа сброшенных бомб обоими бомбардировщиками (т. е. ограничиться возможными значениями X, равными 1, 2, 3 и 4).
Решение: Пусть события Ai и Вi — попадание в цель соответственно первой и второй бомбой при i-ом сбрасывании Ai и Bi— промахи.
Найдем закон распределения случайной величины X—числа израсходованных первым и вторым бомбардировщиком бомб.
Бомбардировщики израсходуют одну бомбу (X=1), если первый бомбардировщик попадет в цель: p1=PX=1=PA1=0, 7. Бомбардировщики израсходуют 2 снаряда (X=2), если первый промахнется, а второй попадет в цель: p2=PX=2=PA1B2=0, 3*0, 8=0, 24. Если было израсходовано 3 бомбы (X=3), то только в том случае, если при первом выбросе бомб промазали оба бомбардировщика, а при втором попал первый: p3=PX=3=PA1B1A2=0, 3*0, 2*0, 7=0, 042. Четыре бомбы (X=4) понадобятся 2 бомбардировщикам, если попадет в цель лишь второй бомбардировщик при втором выбросе: p4=PX=4=PA1B1A2B2=0, 3*0, 2*0, 3*0, 8=0, 0144.
Искомый закон распределения дискретной случайной величины X — числа снарядов, израсходованных двумя бомбардировщиками:
| X | ||||
| P | 0, 7 | 0, 24 | 0, 042 | 0, 0144 |
#176
Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0, 0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.
Решение. По условию n=100 000; p=0. 0001; k=5. События, состоявшие в том, что книги сброшюрованы неправильно, независимы, число n велико, а вероятность p мала, поэтому воспользуемся распределением Пуассона:
Pn(k)=λ ke-λ /k
Найдем λ:
λ =np=100 000 * 0, 0001=10
Искомая вероятность:
P100 000(5)=105*e-10/5=105*0, 000045/120=0, 0375
#177
Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени Т равна 0, 002. Найти вероятность того, что за время Т откажут ровно три элемента. УКАЗАНИЕ: принять 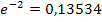 .
.
РЕШЕНИЕ.
По условию 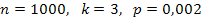 . Отказ любого элемента в течение времени не зависит от событий в предшествующие моменты времени. Так как число n велико, а вероятность p мала, следует воспользоваться распределением Пуассона (
. Отказ любого элемента в течение времени не зависит от событий в предшествующие моменты времени. Так как число n велико, а вероятность p мала, следует воспользоваться распределением Пуассона ( 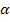 – это среднее число появлений события в n испытаниях; оно обозначается буквой «лямбда», но MSWord такой буквы не знает):
– это среднее число появлений события в n испытаниях; оно обозначается буквой «лямбда», но MSWord такой буквы не знает):
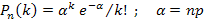
Подставим значения: 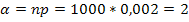
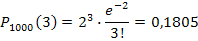
#178
Условие:
Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 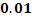 . Найти вероятность того, что среди
. Найти вероятность того, что среди 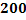 деталей окажется ровно
деталей окажется ровно 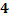 бракованных.
бракованных.
Решение:
По условию, 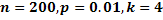 . События, состоящие в том, что детали окажутся бракованными, независимы, число
. События, состоящие в том, что детали окажутся бракованными, независимы, число 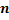 велико, а вероятность
велико, а вероятность 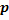 мала, поэтому воспользуемся распределение Пуассона:
мала, поэтому воспользуемся распределение Пуассона:
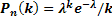
Найдем 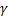 :
:
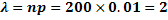
Искомая вероятность:
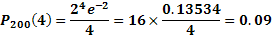
#179
Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0, 002. Найти вероятности того, что в пути будет повреждено изделий: а) ровно три; б) менее трех; в) более трех; г) хотя бы одно.
Решение:
Число n=500 велико, вероятность q= 0, 002 мала и рассматриваемые события (повреждения изделий) независимы, поэтому имеет место формула Пуассона.
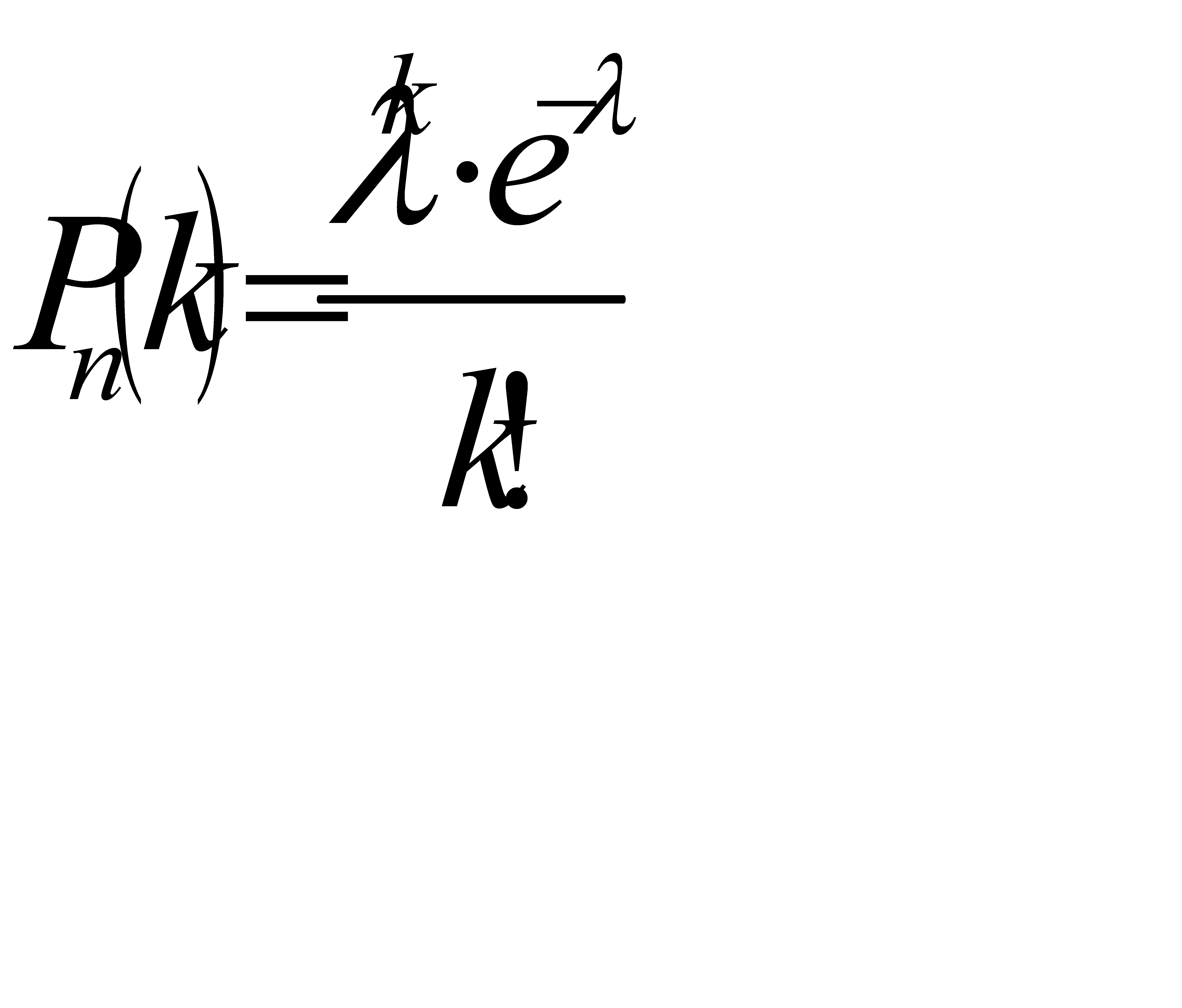 .
.
а) Найдем 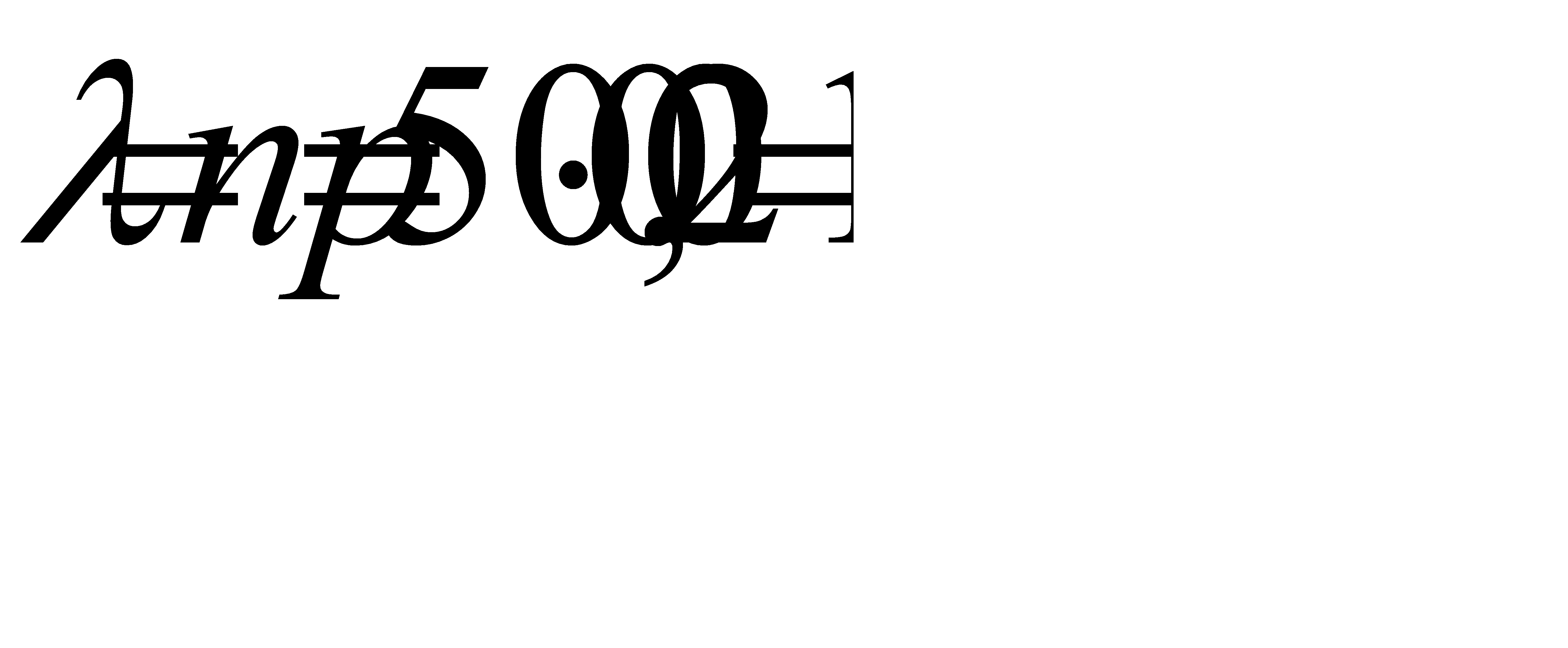
Найдем вероятность того, что будет повреждено ровно 3 изделия:
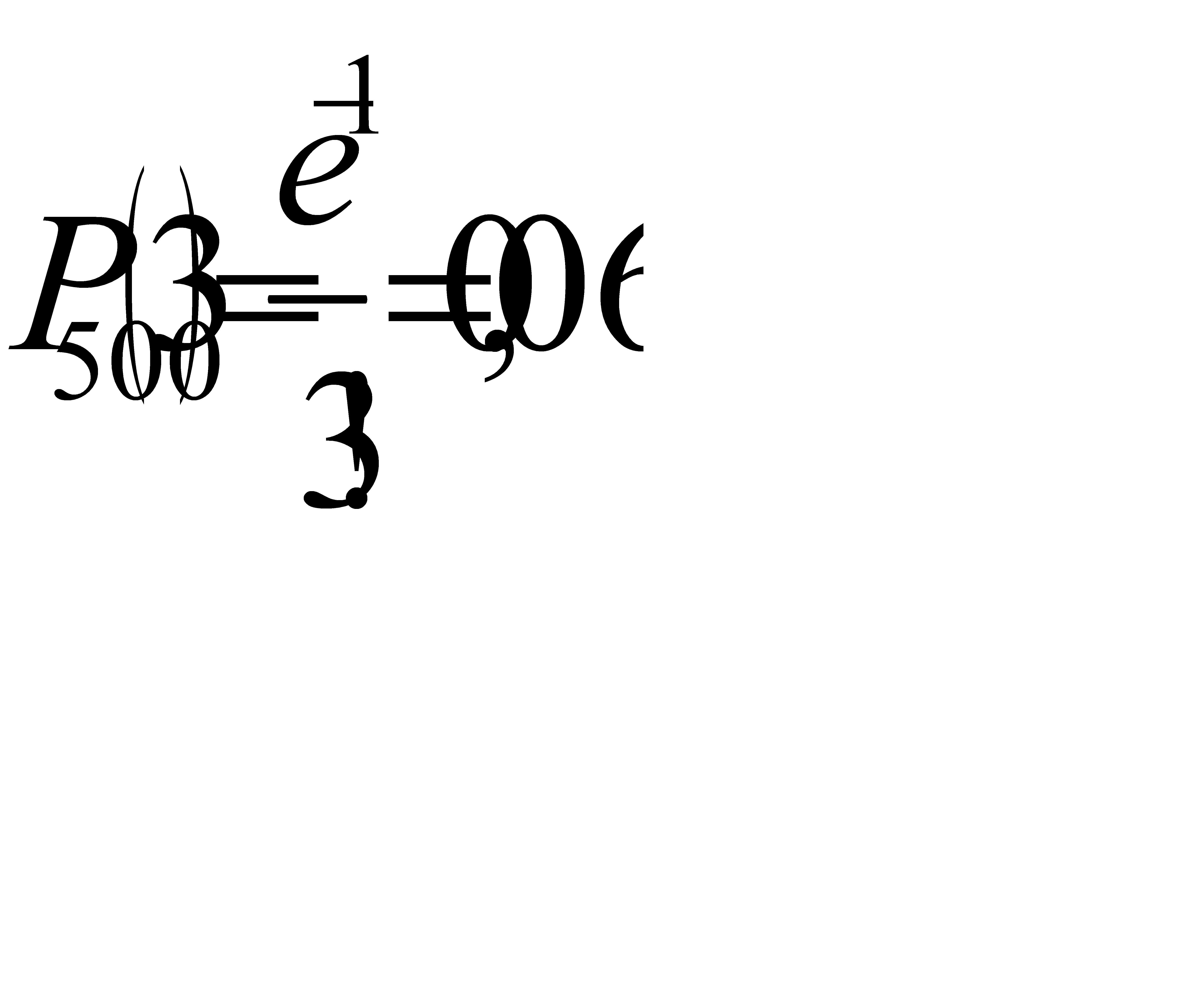
б) Найдем вероятность того, что будет повреждено менее трех изделий:
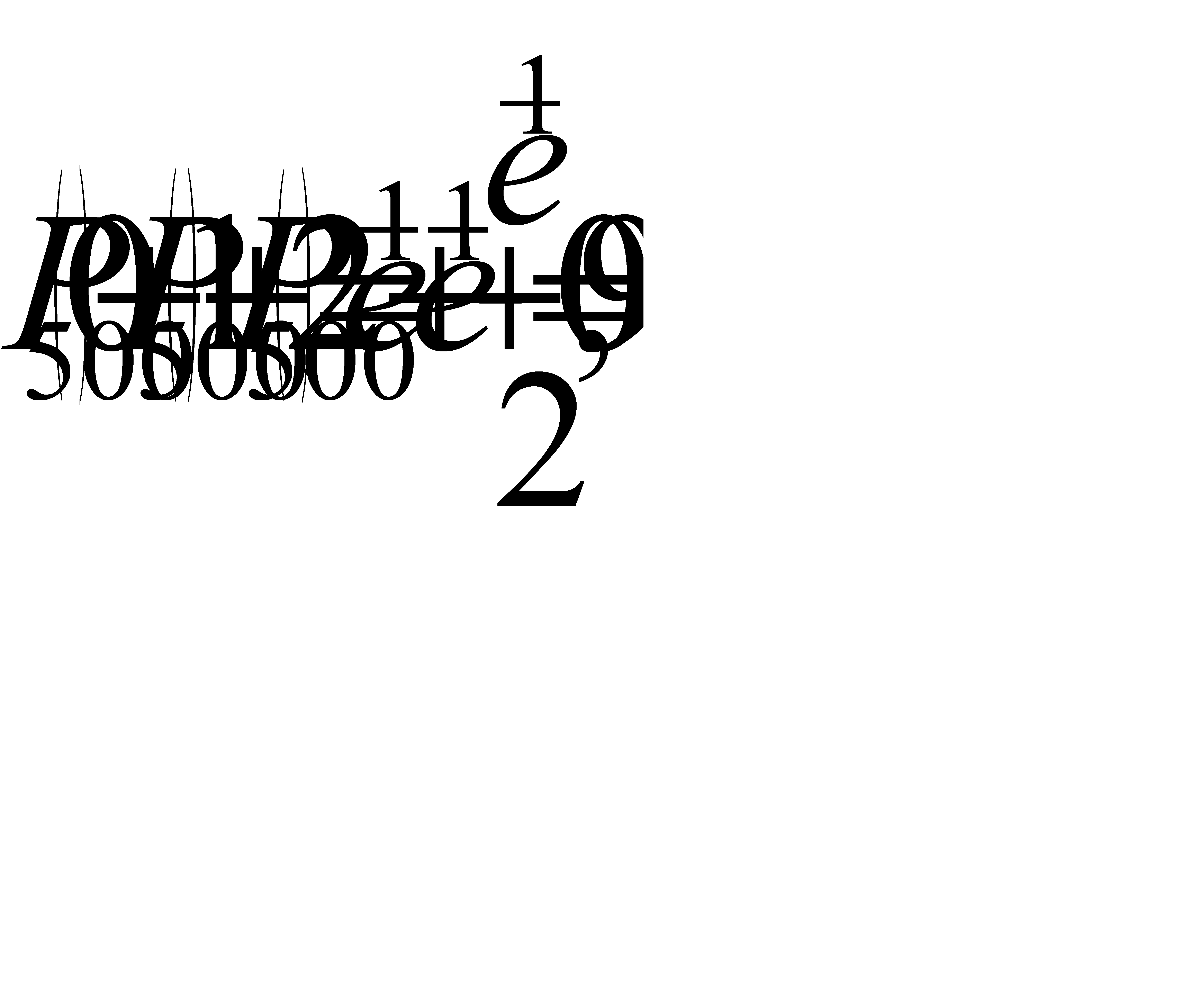
в) Найдем вероятность Р того, что будет повреждено более трех изделий. События «повреждено более трех изделий» и «повреждено не более трех изделий»(обозначим вероятность этого события через Q) – противоположны, поэтому P=1-Q. Отсюда

Используя результаты, полученные выше, имеем
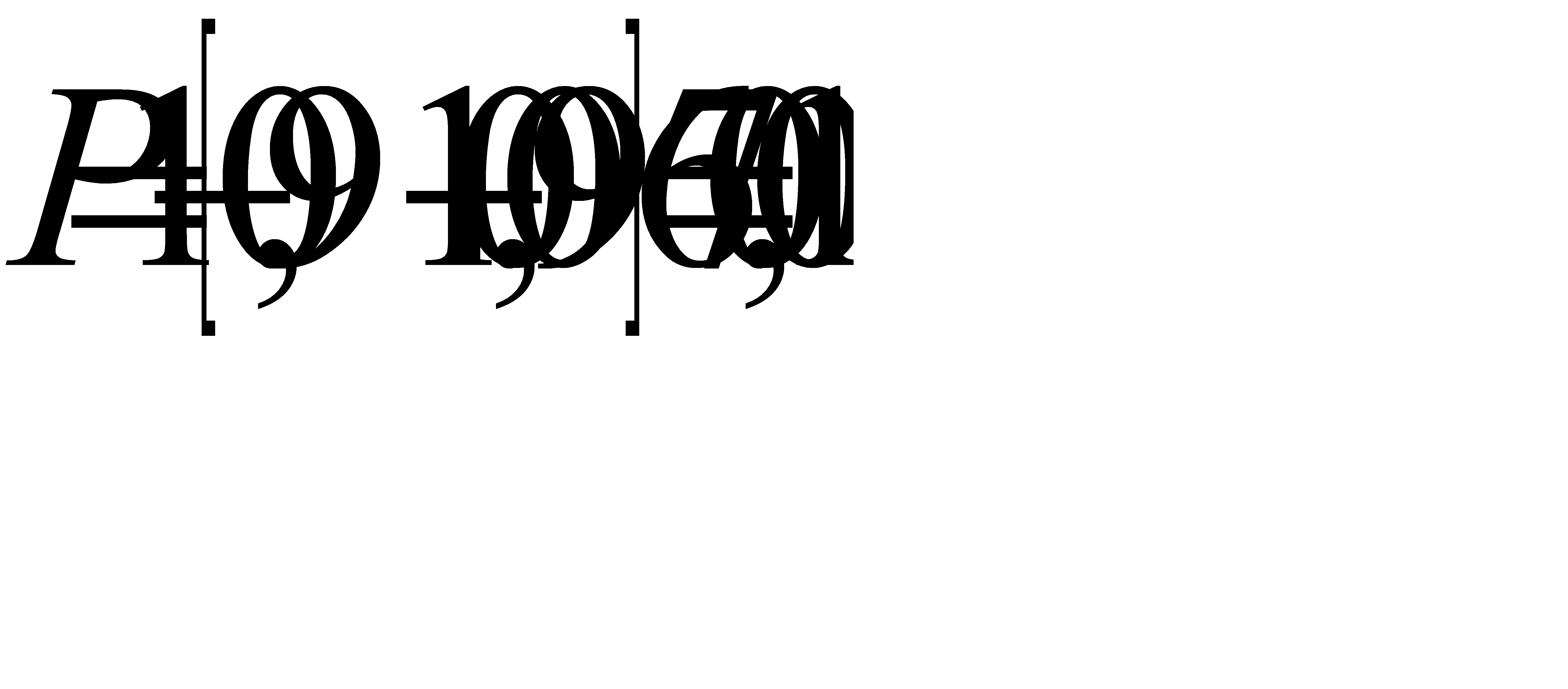 .
.
г)Найдем вероятность того, что будет повреждено хотя бы одно изделие. События «повреждено хотя бы одно изделие» и «ни одно изделие не повреждено» (обозначим вероятность этого события через Q)- противоположные, следовательно P=1-Q. Отсюда искомая вероятность того, что будет повреждено хотя бы одно изделие, равна

#180
Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0, 003. Найти вероятности того,
что магазин получит разбитых бутылок: а) ровно две; б) менее двух;
в) более двух; г) хотя бы одну. Указание. Принять е 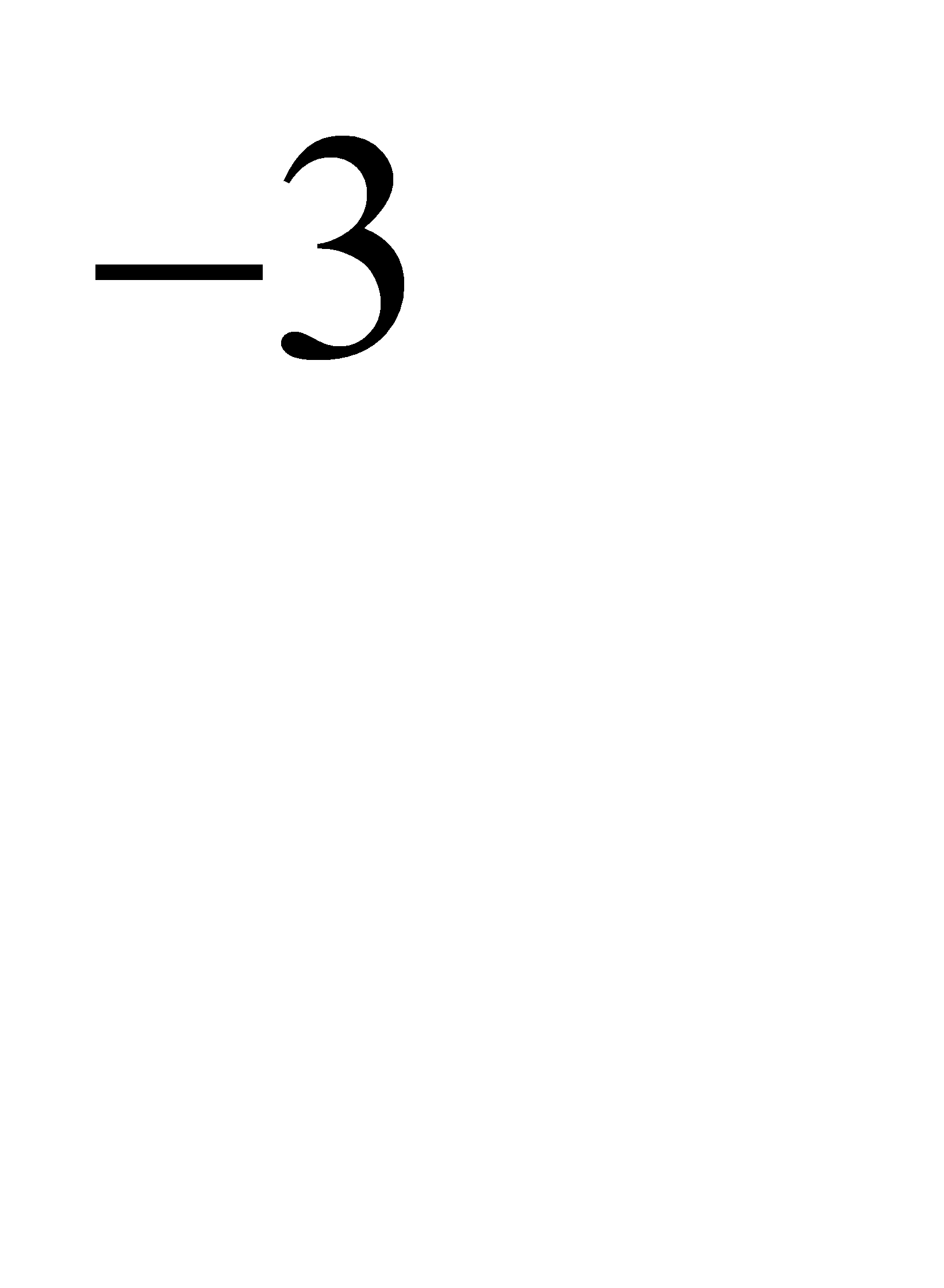 =0, 04979.
=0, 04979.
Решение:
Число n=1000 слишком велико, а вероятность мала, а рассматриваемые события независимы, поэтому имеет место теорема Пуассона:
 где
где  , a е
, a е 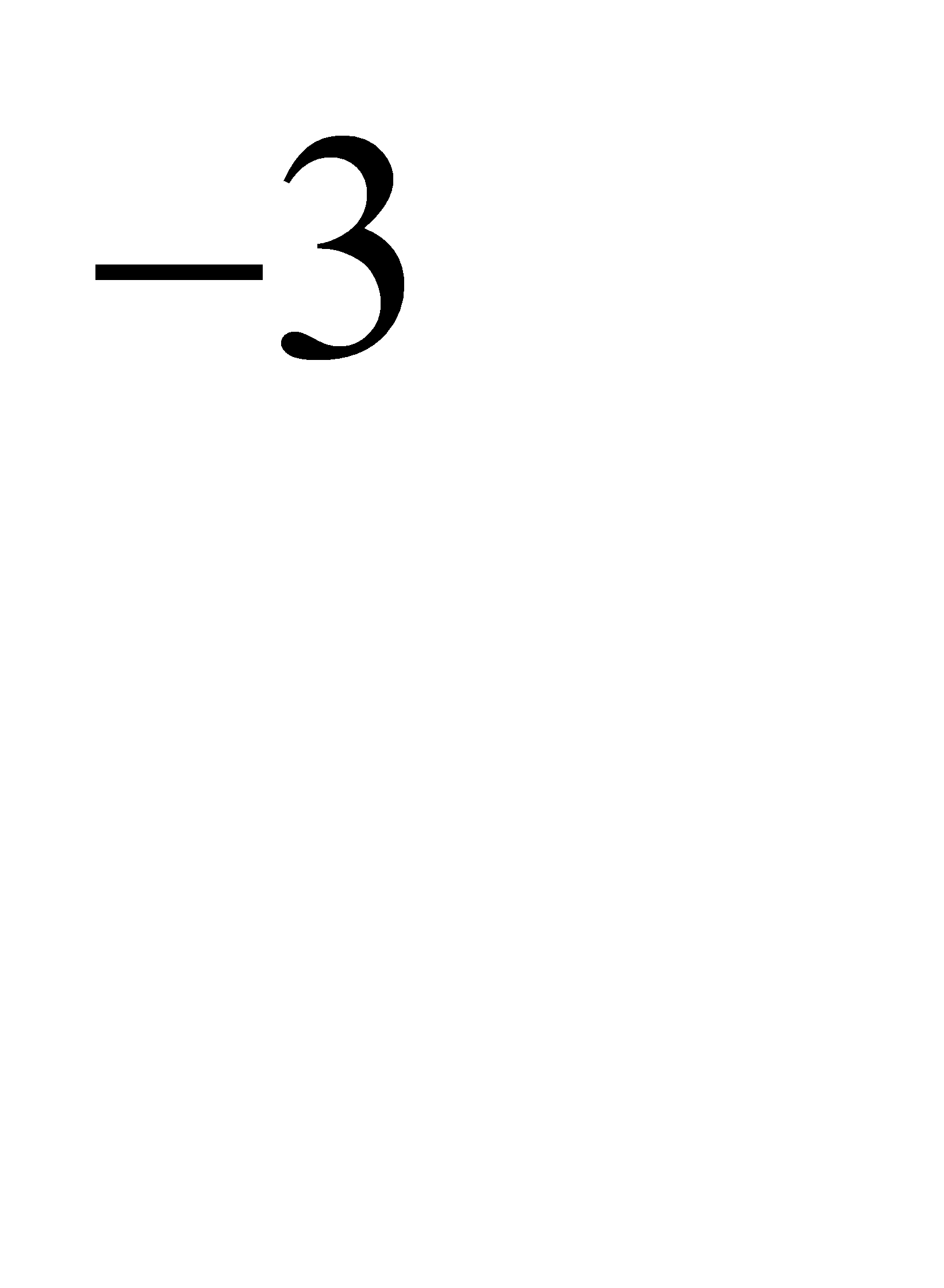 =0, 04979
=0, 04979
Воспользовавшись этой теоремой получим:
а) 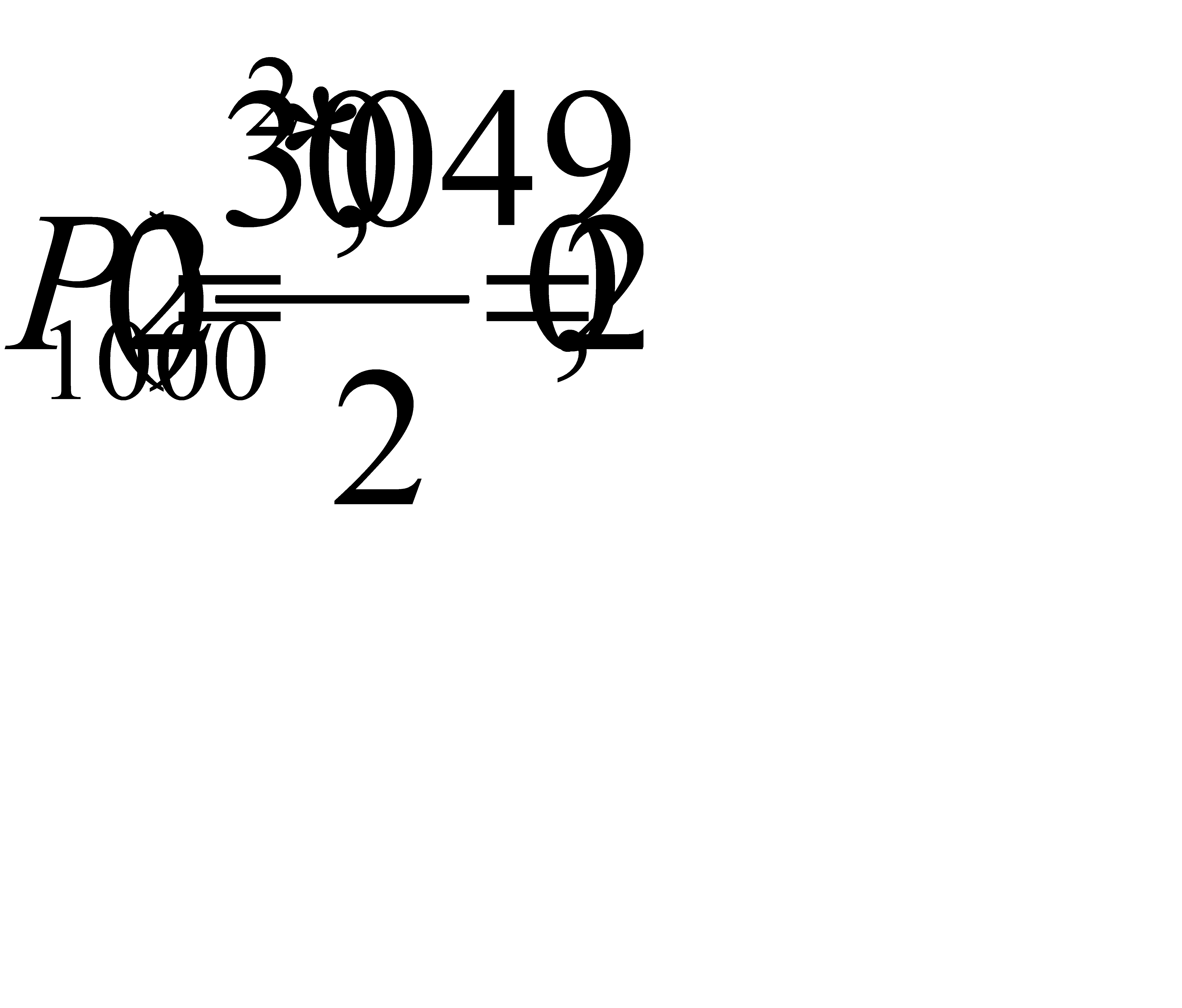
б) 
в)Эта задача равносильна следующей задаче:
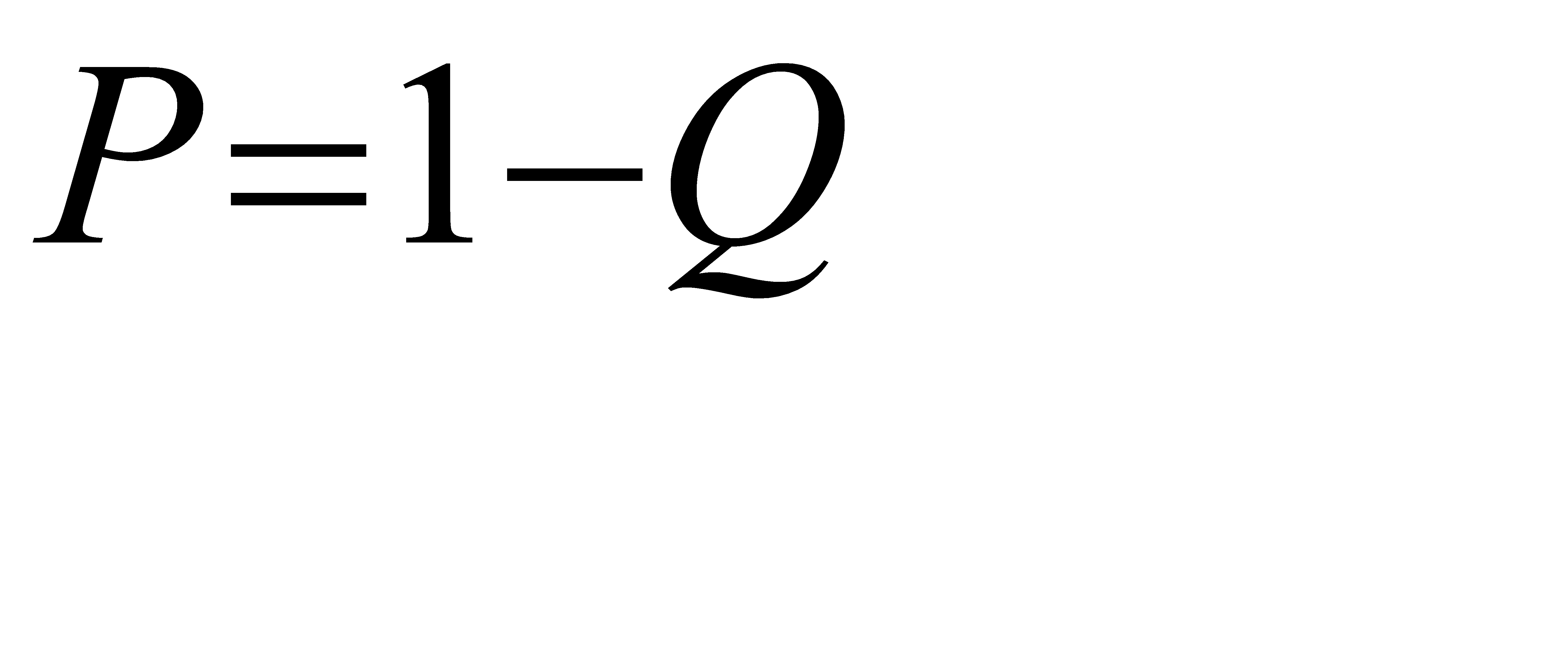 где Q=
где Q=  =0, 224+0, 1992=0, 423;
=0, 224+0, 1992=0, 423; 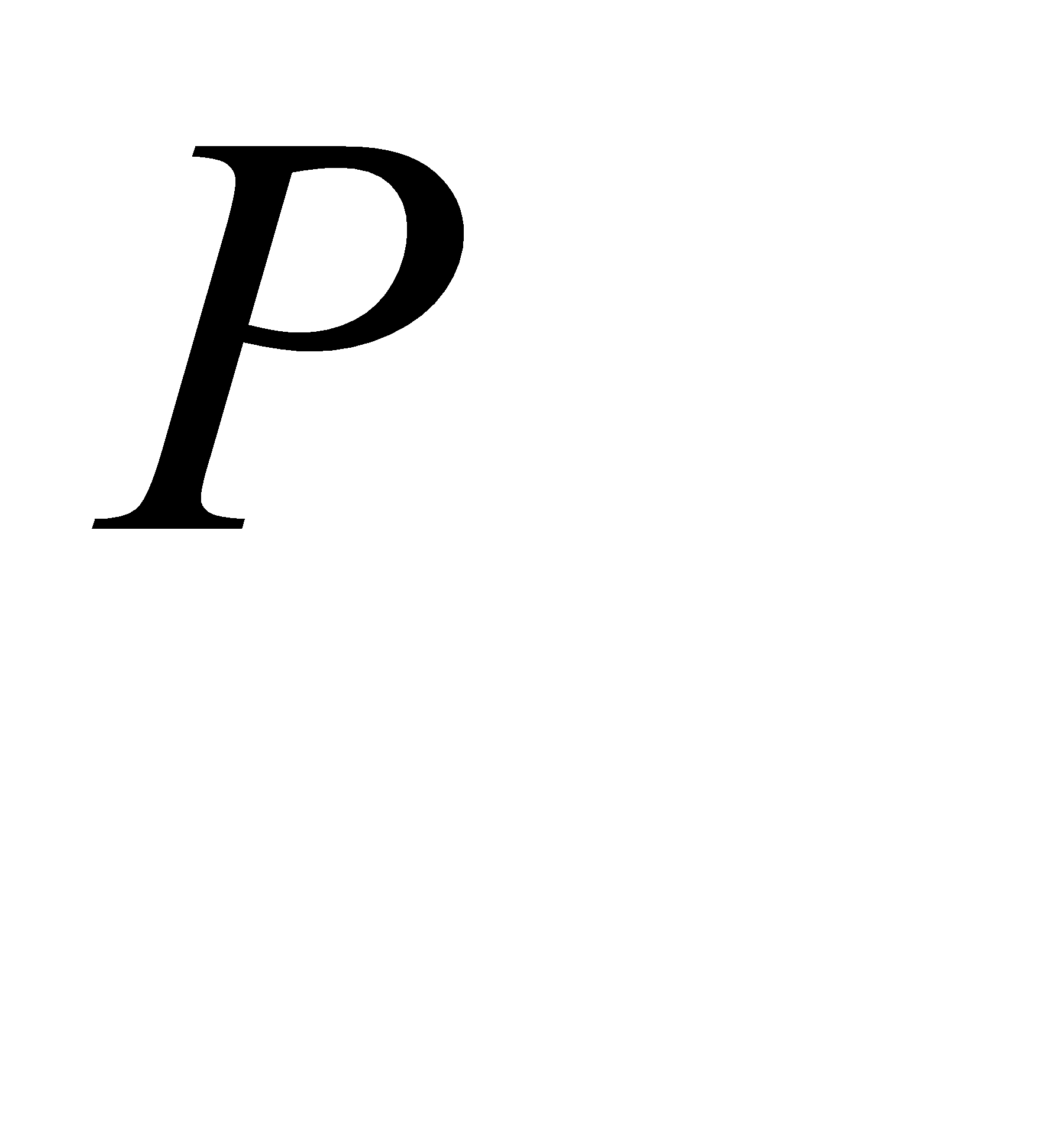 =1-0, 423=0, 576
=1-0, 423=0, 576
г)Это равносильно задаче Р=1-Q, где 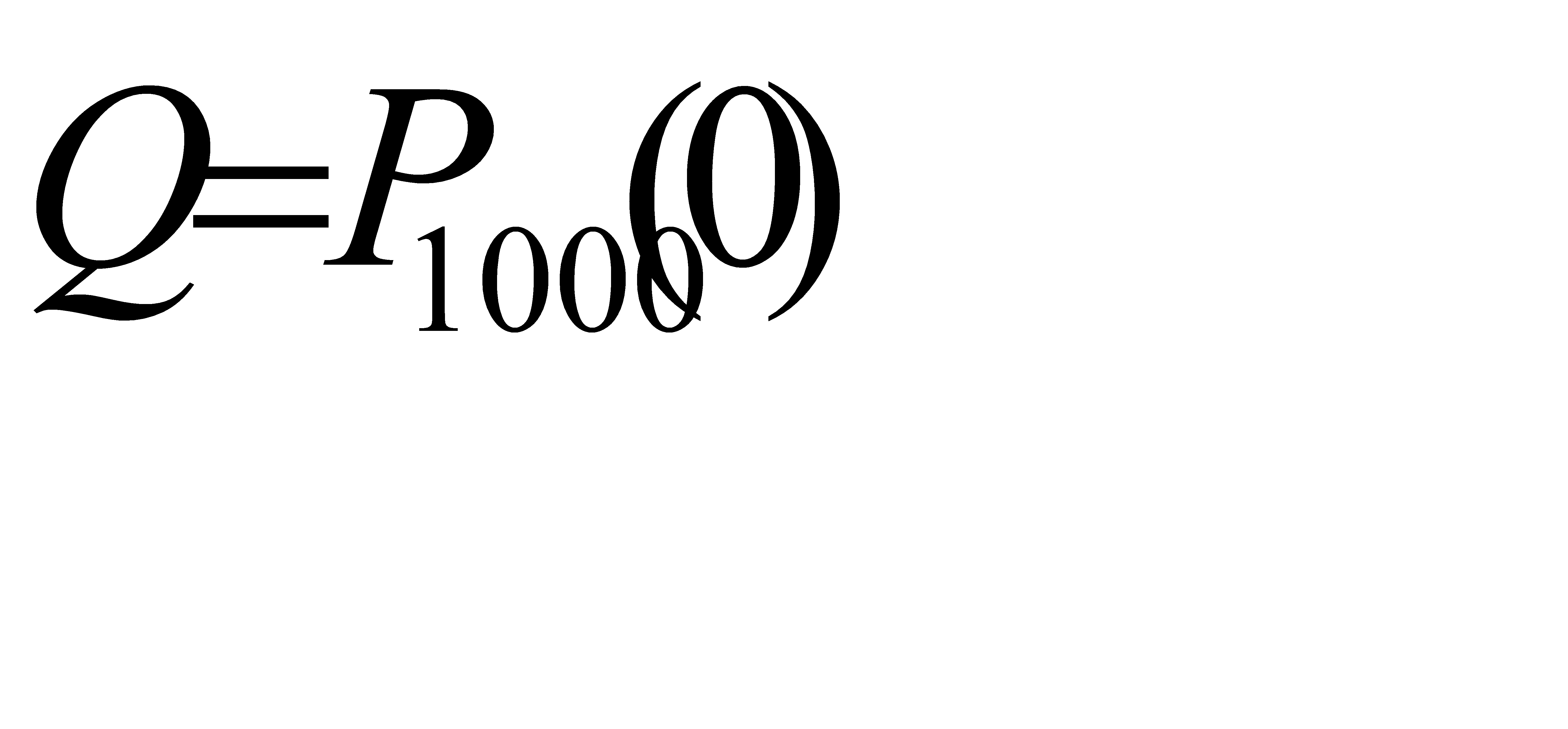

Ответ: а)0, 224; б)0, 1992; в)0, 576; г)0, 95
#181
а) Устройство состоит из большого числа независимо работающих элементов с одинаковой (очень малой) вероятностью отказа каждого элемента за время T. Найти среднее число отказавших за время T элементов, если вероятность того, что за это время откажет хотя бы один элемент, равна 0, 98.
Решение
Из условии задачи следует (поскольку число элементов велико, элементы работают независимо и вероятность отказа каждого элемента мала), что число отказов распределено по закону Пуассона, причём требуется найти параметр 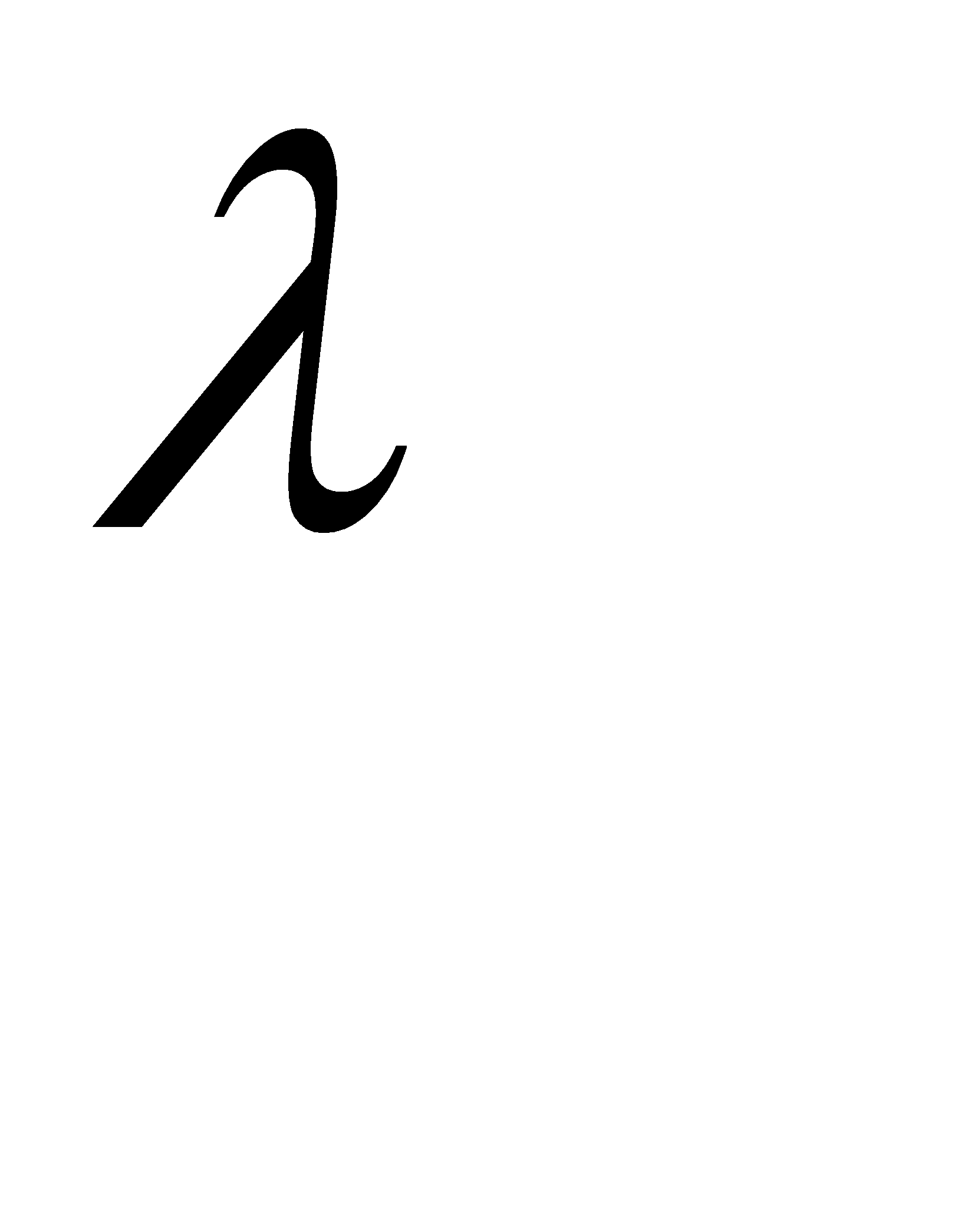 (среднее число отказов).
(среднее число отказов).
Вероятность того, что откажет хотя бы один элемент, по условию равна 0, 98, следовательно 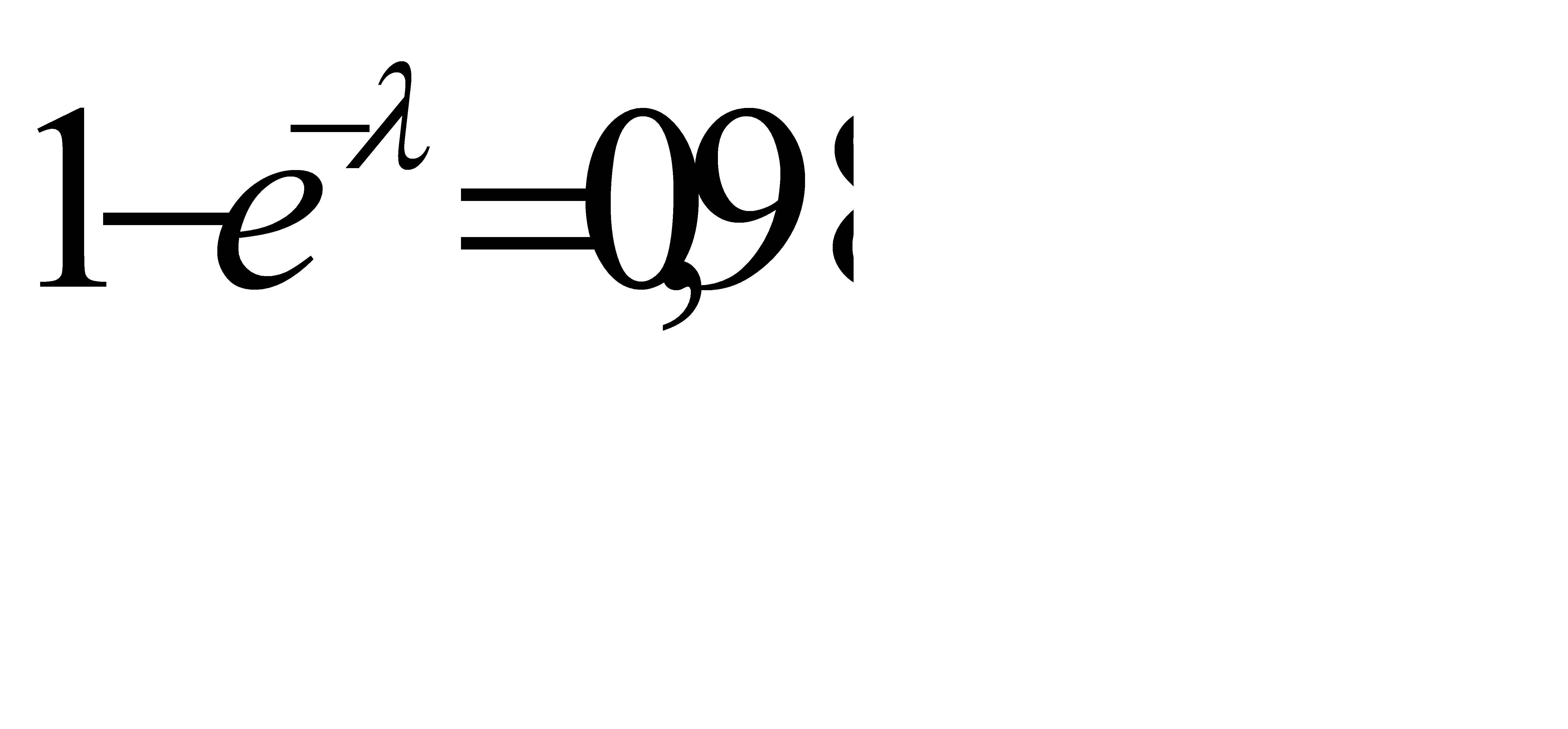 .
.
Отсюда
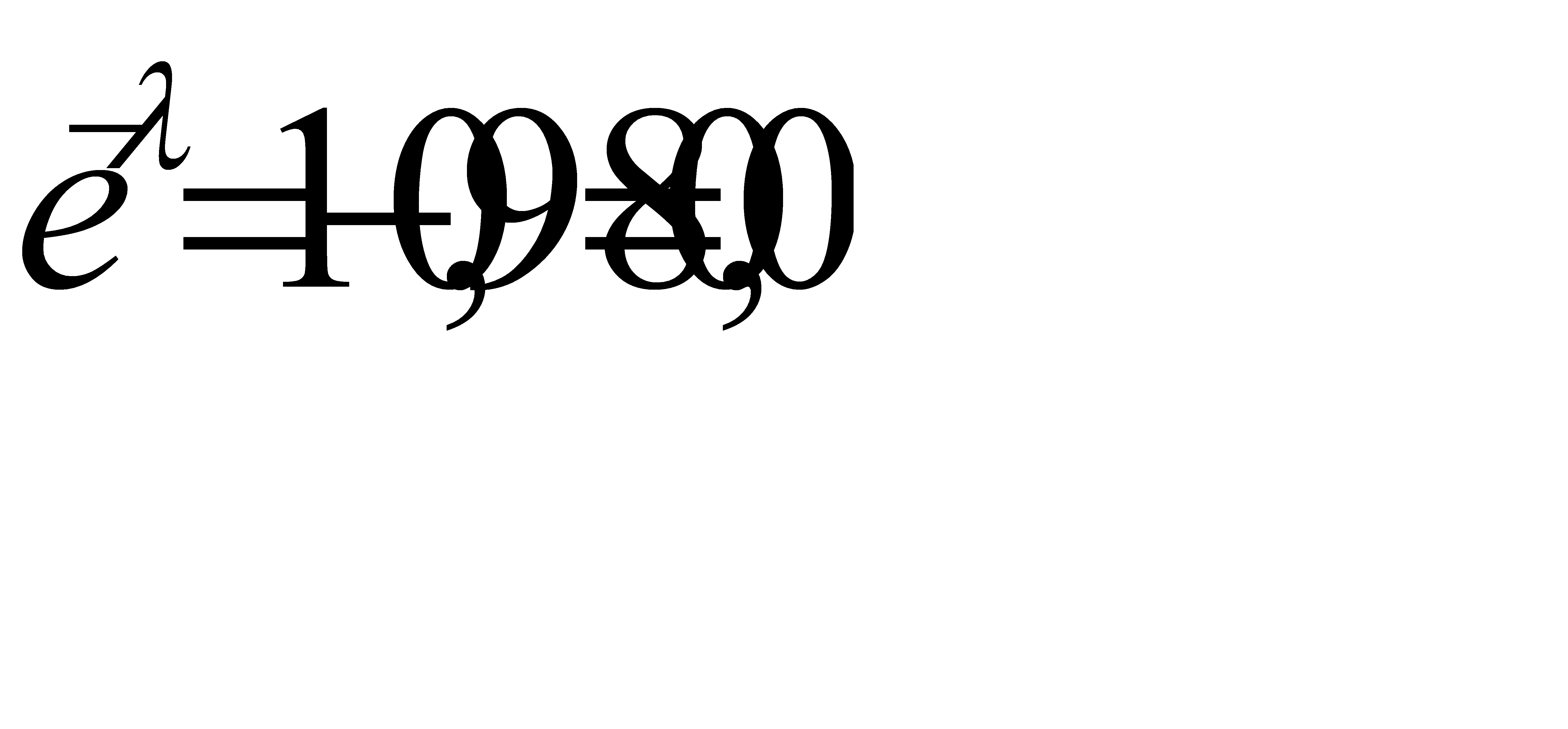
По таблице функции 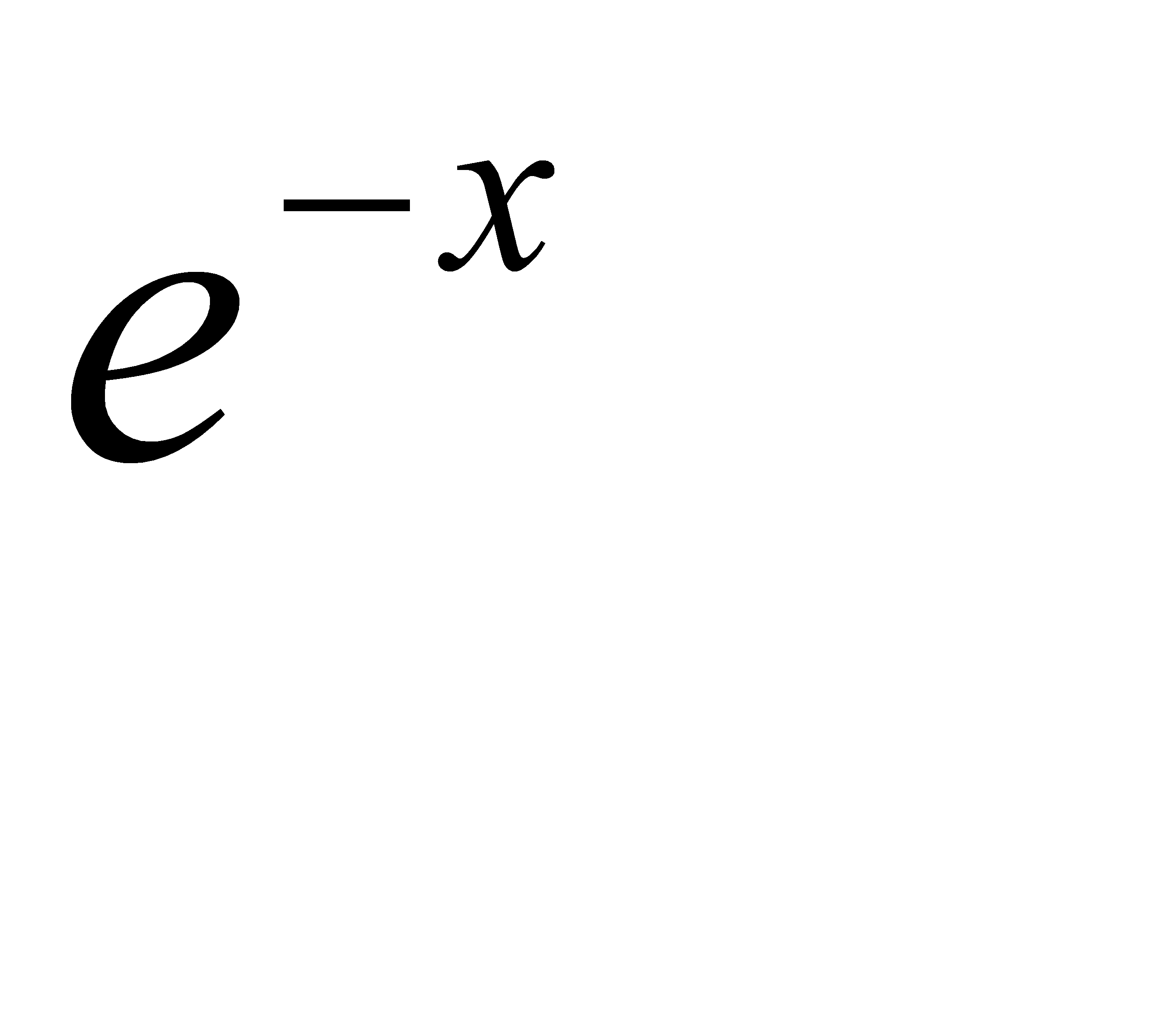 находим
находим 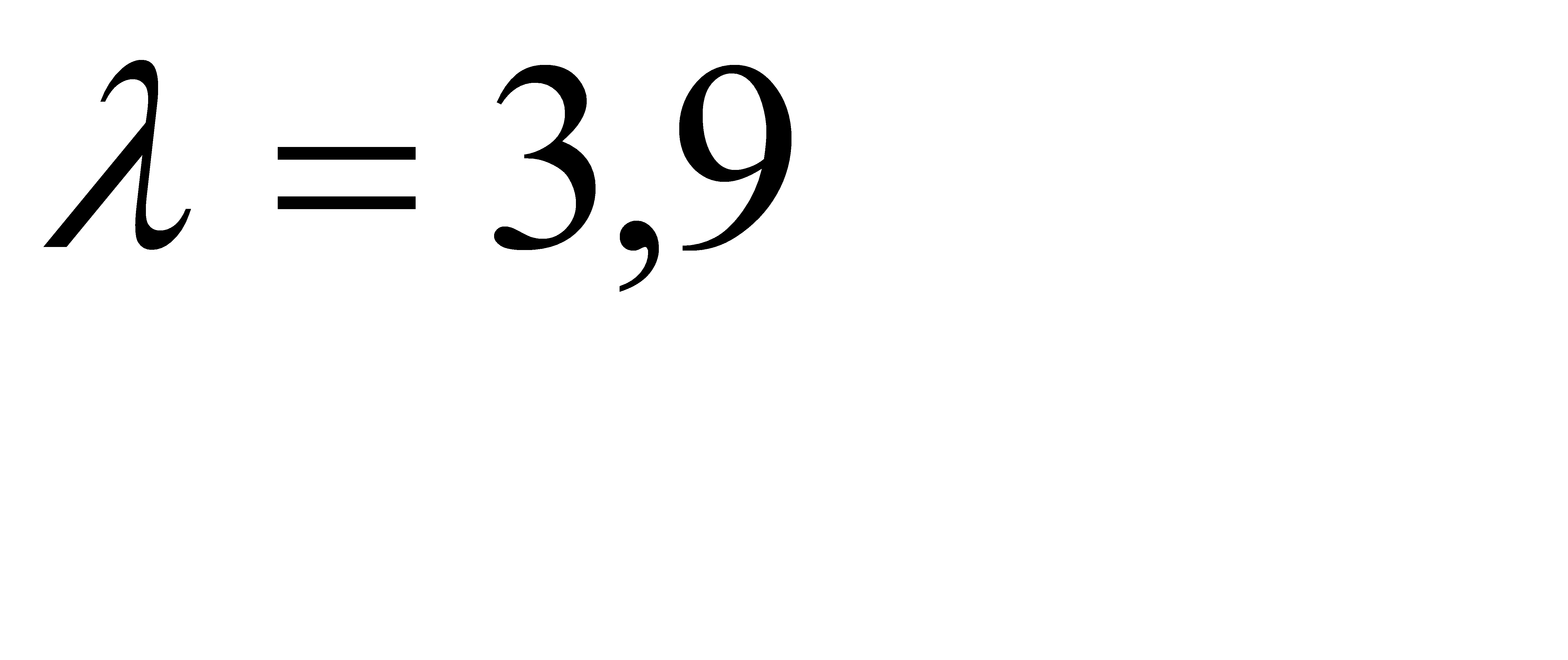 . Итак, за время T работы устройства откажет примерно 4 элемента.
. Итак, за время T работы устройства откажет примерно 4 элемента.
Ответ:  элемента
элемента
б) Найти среднее число 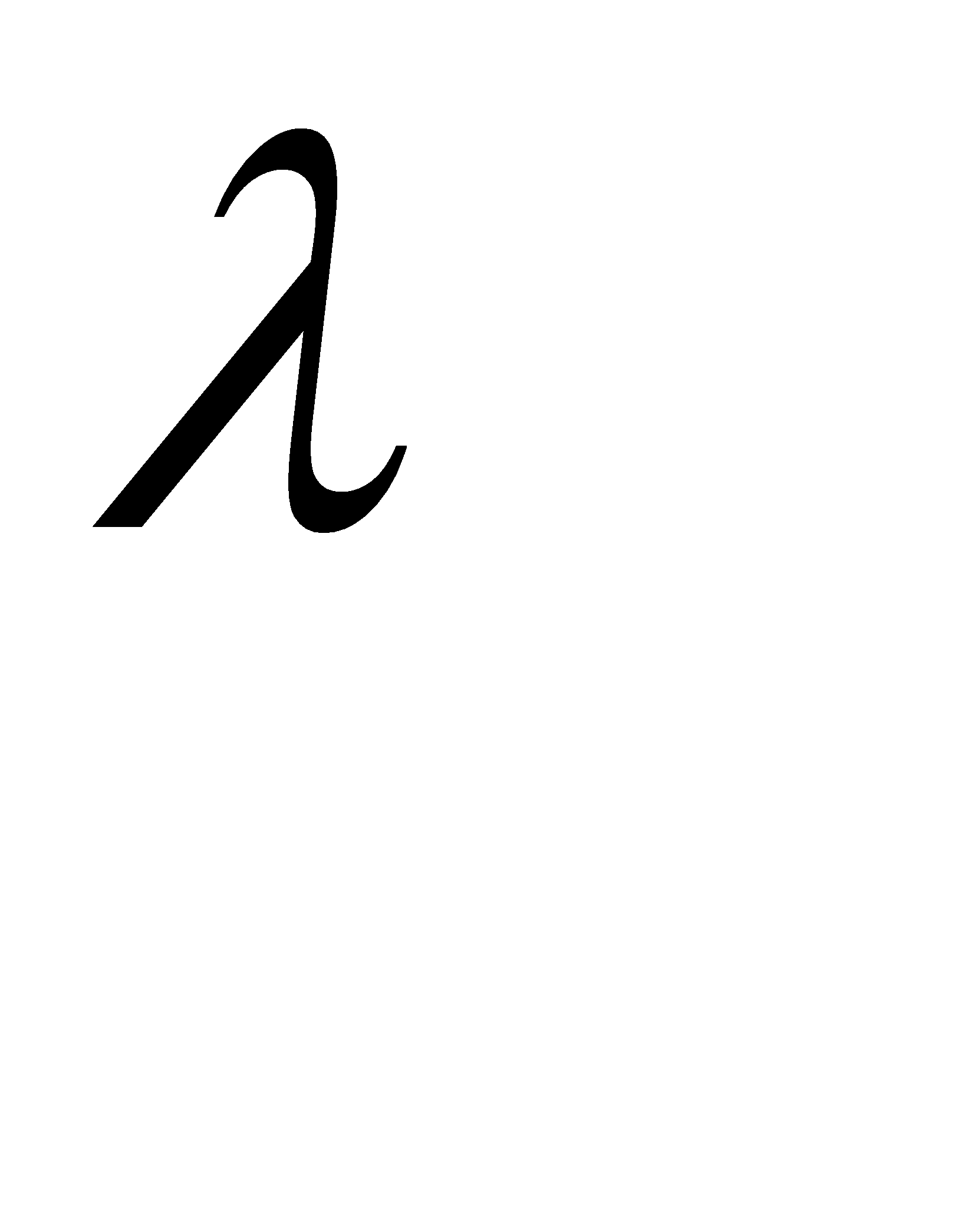 бракованных изделий в партии изделий, если вероятность того, что в этой партии содержится хотя бы одно бракованное изделие, равна 0, 95. Предполагается, что число бракованных изделий в рассматриваемой партии распределено по закону Пуассона.
бракованных изделий в партии изделий, если вероятность того, что в этой партии содержится хотя бы одно бракованное изделие, равна 0, 95. Предполагается, что число бракованных изделий в рассматриваемой партии распределено по закону Пуассона.
Решение
Т. к вероятность того, что в этой партии содержится хотя бы одно бракованное изделие, равна 0, 95, то 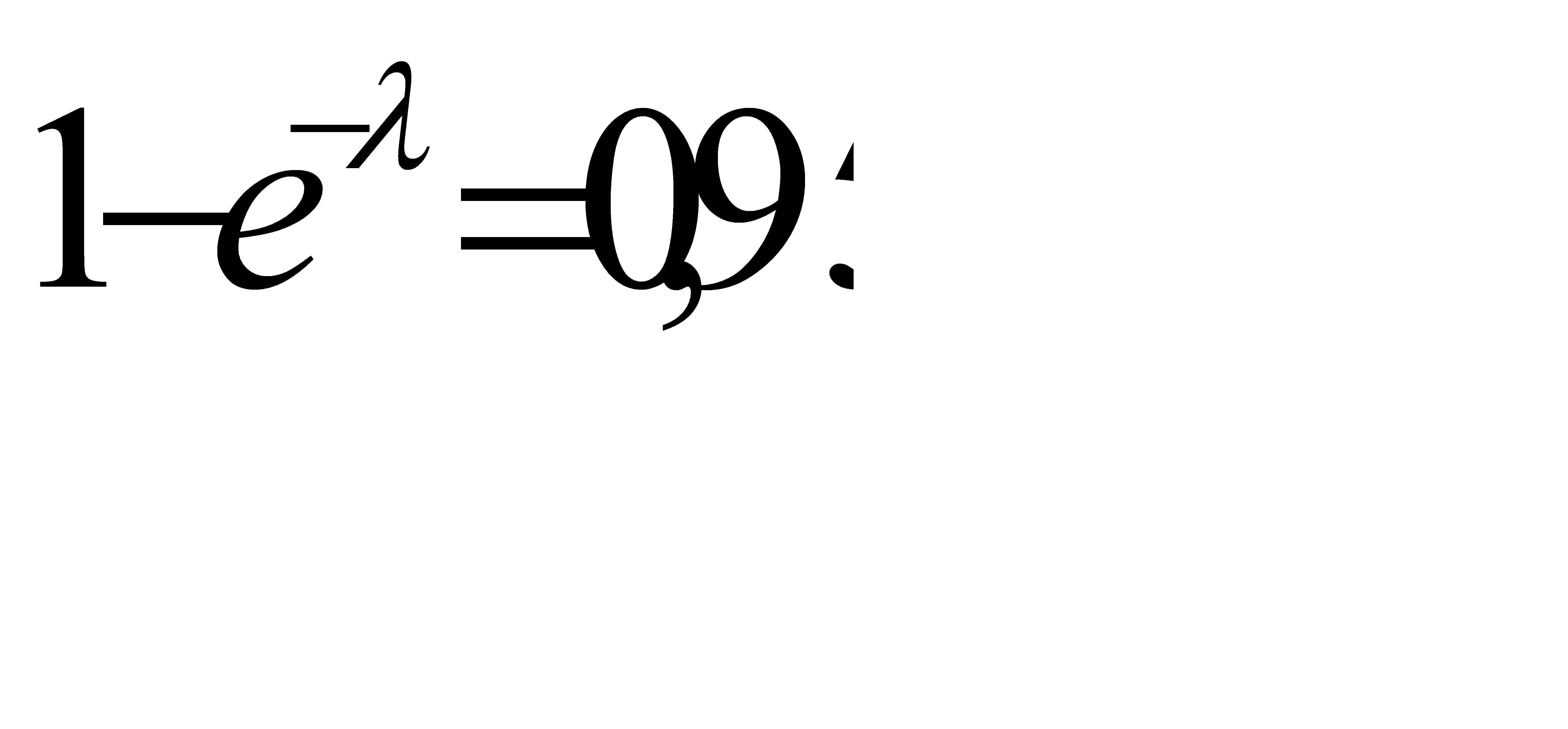
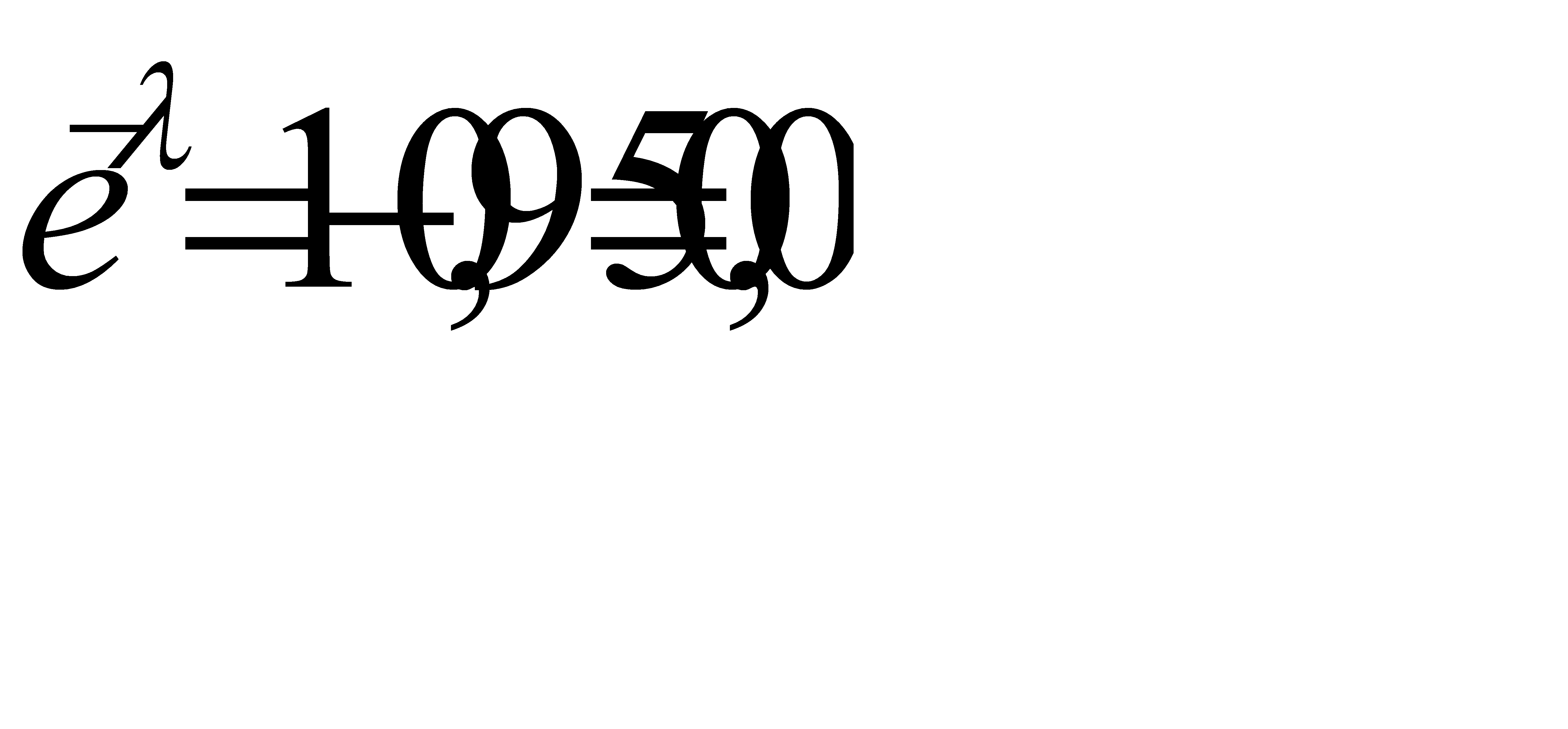
По таблице функции 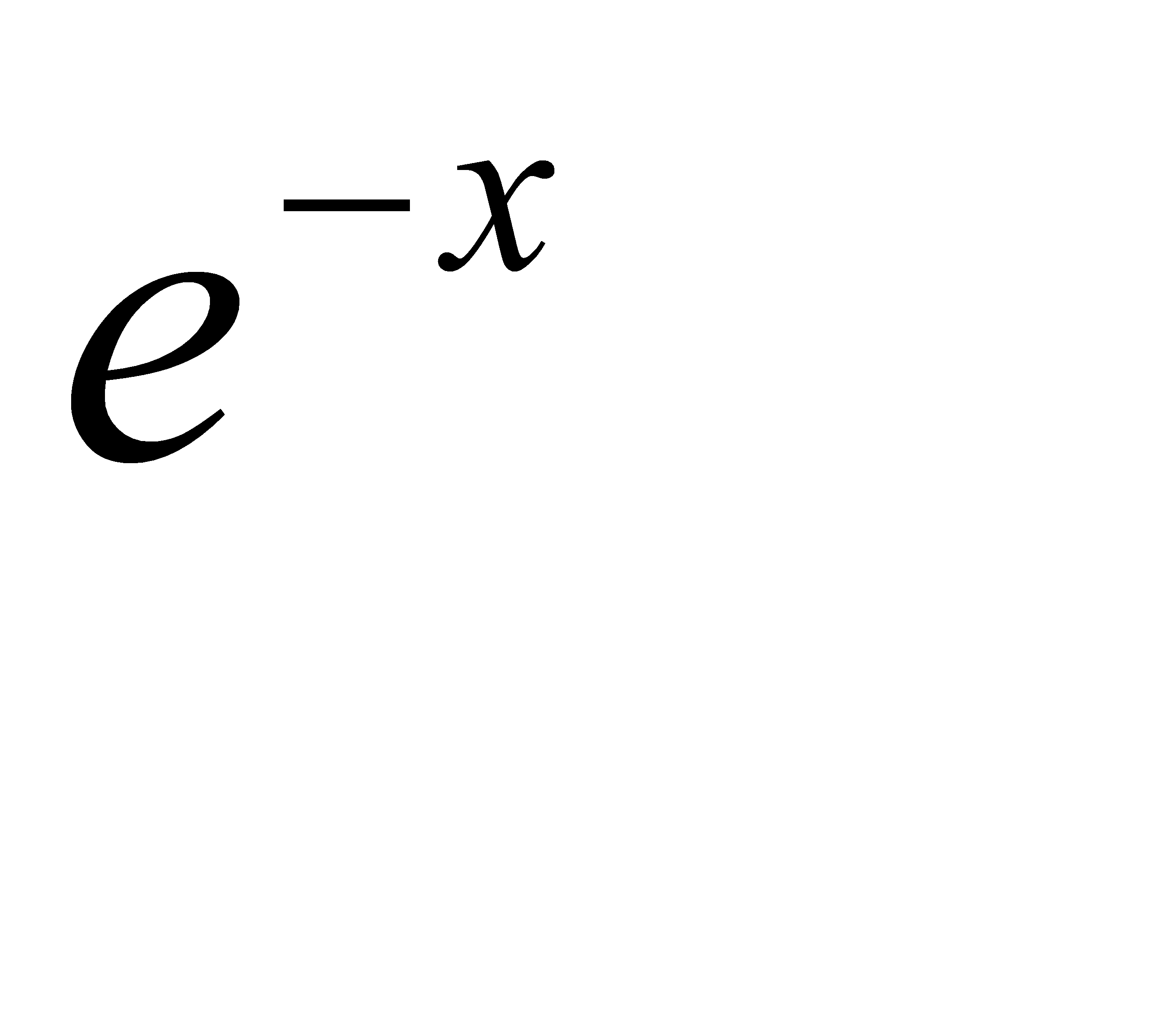 находим
находим 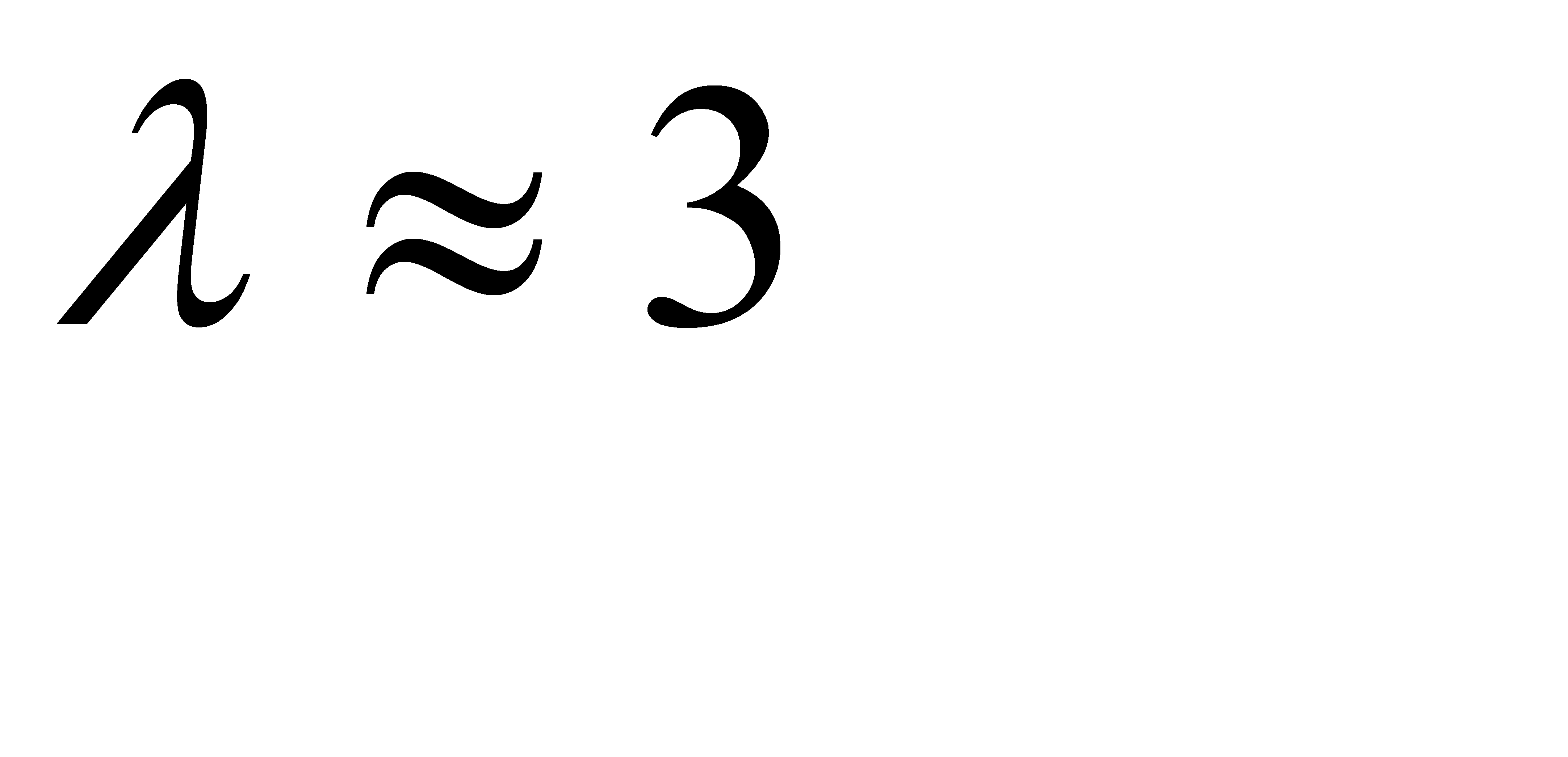 . Итак, среднее число бракованных изделий равно 3.
. Итак, среднее число бракованных изделий равно 3.
Ответ: 3
#182
Задание: Доказать, что сумма вероятностей числа появлений события в независимых испытаниях, вычисленных по закону Пуассона, равна единице. Предполагается, что испытания производятся бесчисленное количество раз.
Решение: В силу закона Пуассона 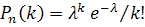
Используем разложение функции ex в ряд Маклорена:
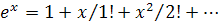
Известно, что этот ряд сходится при любом значении 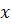 , поэтому,
, поэтому,
положив 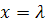 , получим
, получим
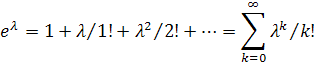
Найдем искомую сумму вероятностей 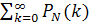 , учитывая, что
, учитывая, что 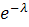 не зависит от
не зависит от 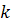 и, следовательно, может быть вынесено за знак суммы:
и, следовательно, может быть вынесено за знак суммы:
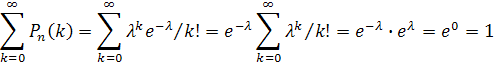
Замечание. Утверждение задачи следует немедленно из того, что сумма вероятностей событий, образующих полную группу, равна единице. Приведенное доказательство преследует учебные цели.
#183
Вероятность выигрыша по одному лотерейному билету  .
.
Сколько нужно купить билетов, чтобы выиграть хотя бы по одному из них с вероятностью 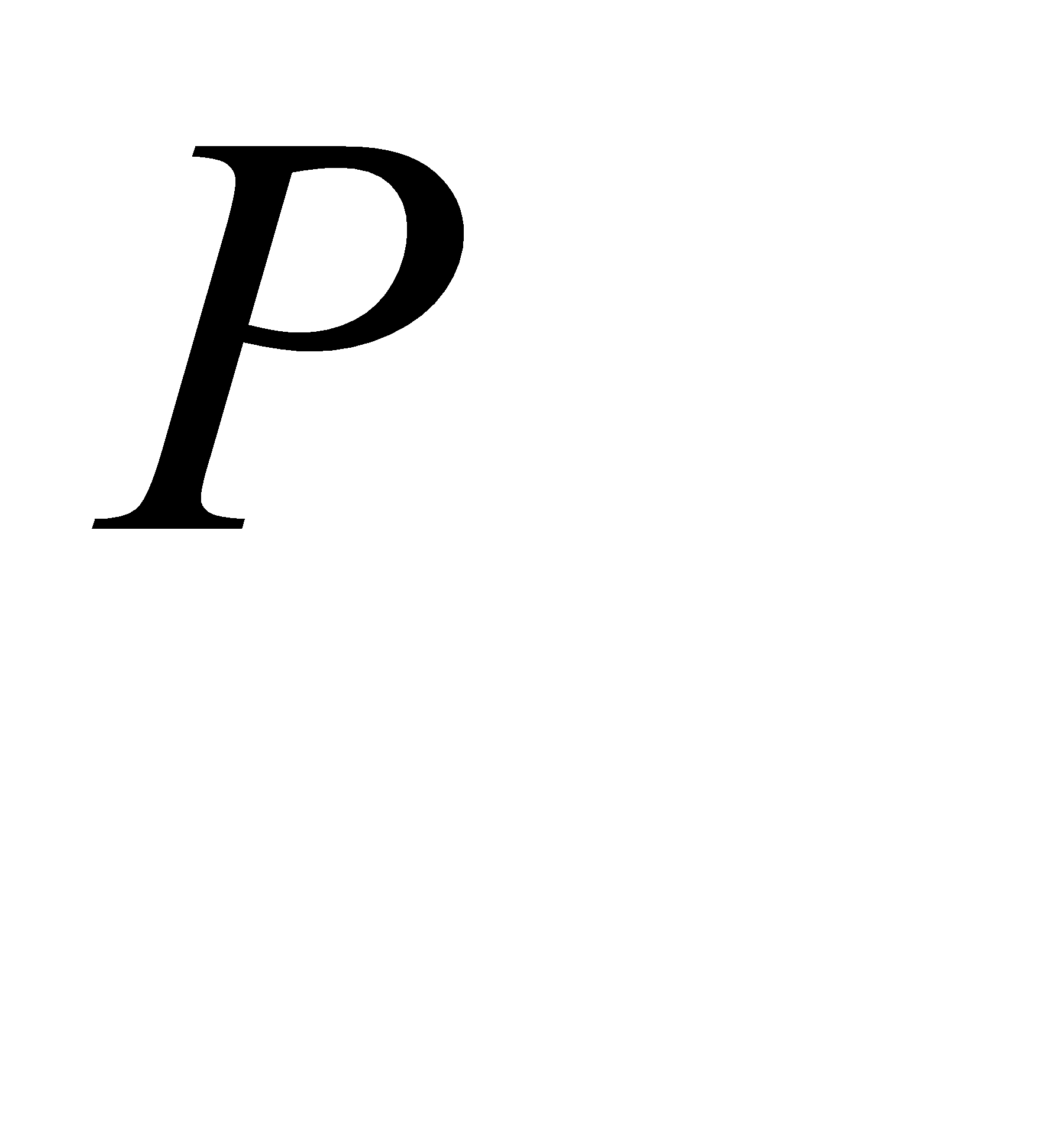 , не меньшей, чем
, не меньшей, чем 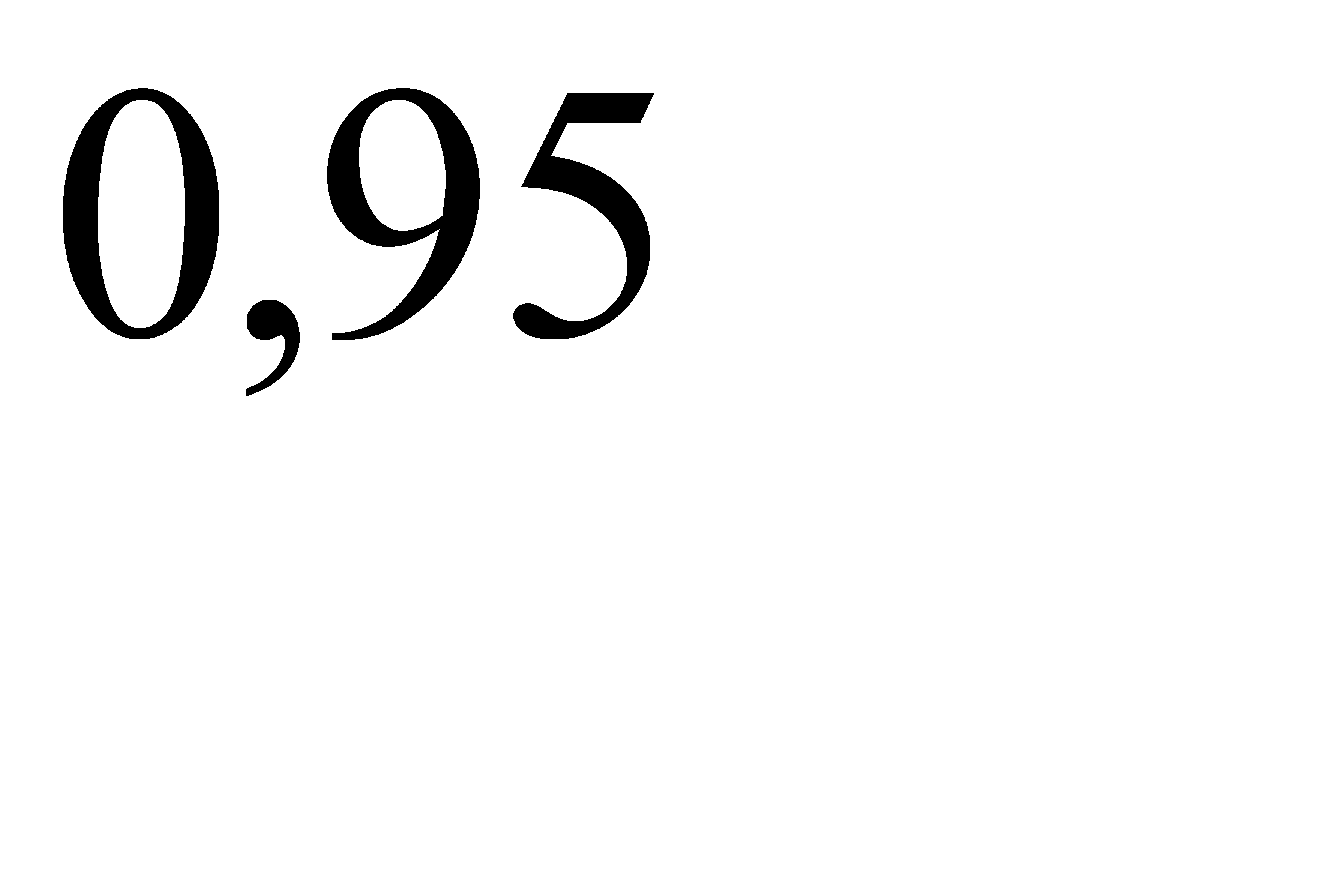 ?
?
Решение:
Вероятность выигрыша мала, а число билетов, которое нужно купить, очевидно, велико, поэтому случайное число выигрышных билетов имеет приближённо распределение Пуассона.
Ясно, что события «ни один из купленных билетов не является выигрышным» и «хотя бы один билет - выигрышный» - противоположные. Поэтому сумма вероятностей этих событий равна единице: Поэтому сумма вероятностей этих событий равна единице:
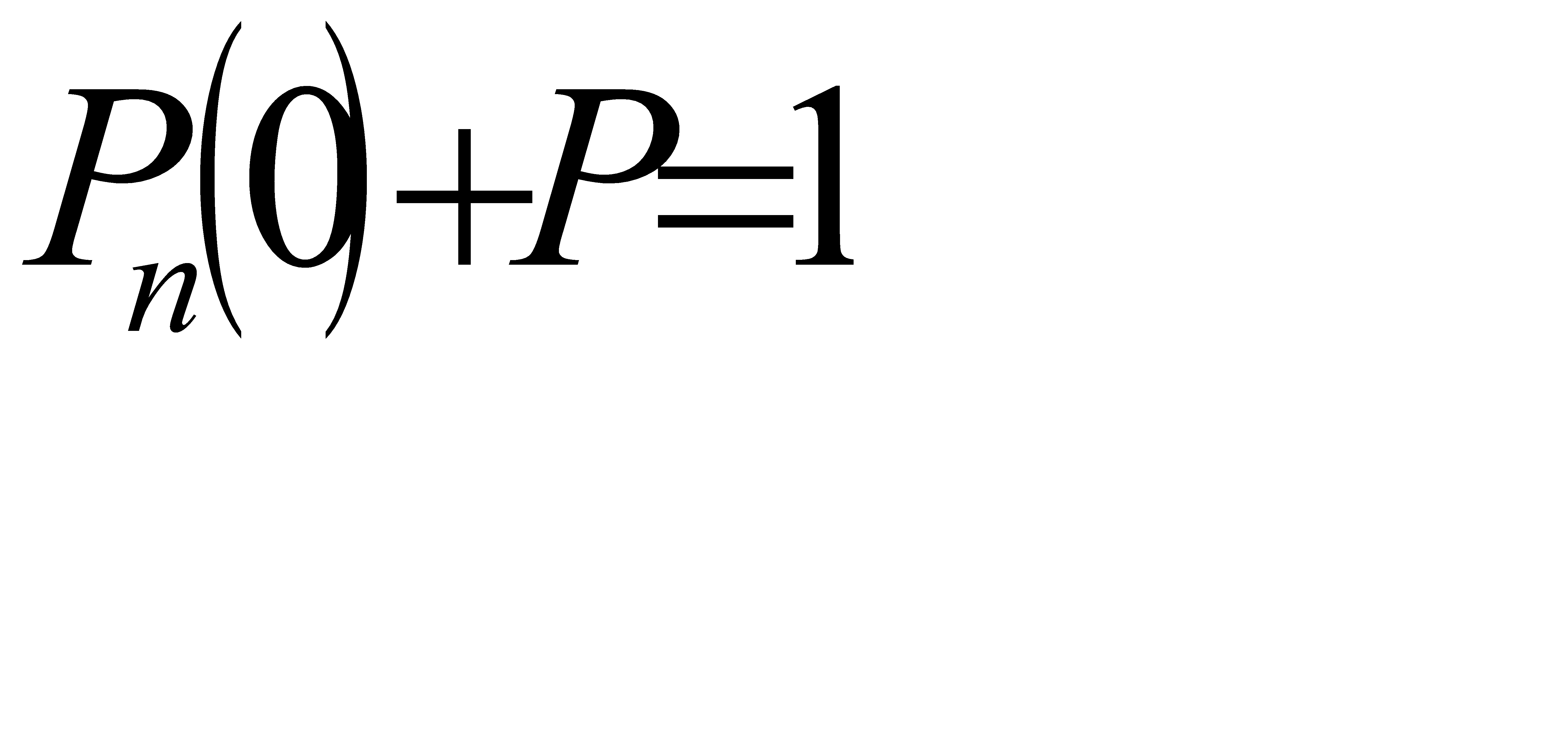 , или
, или 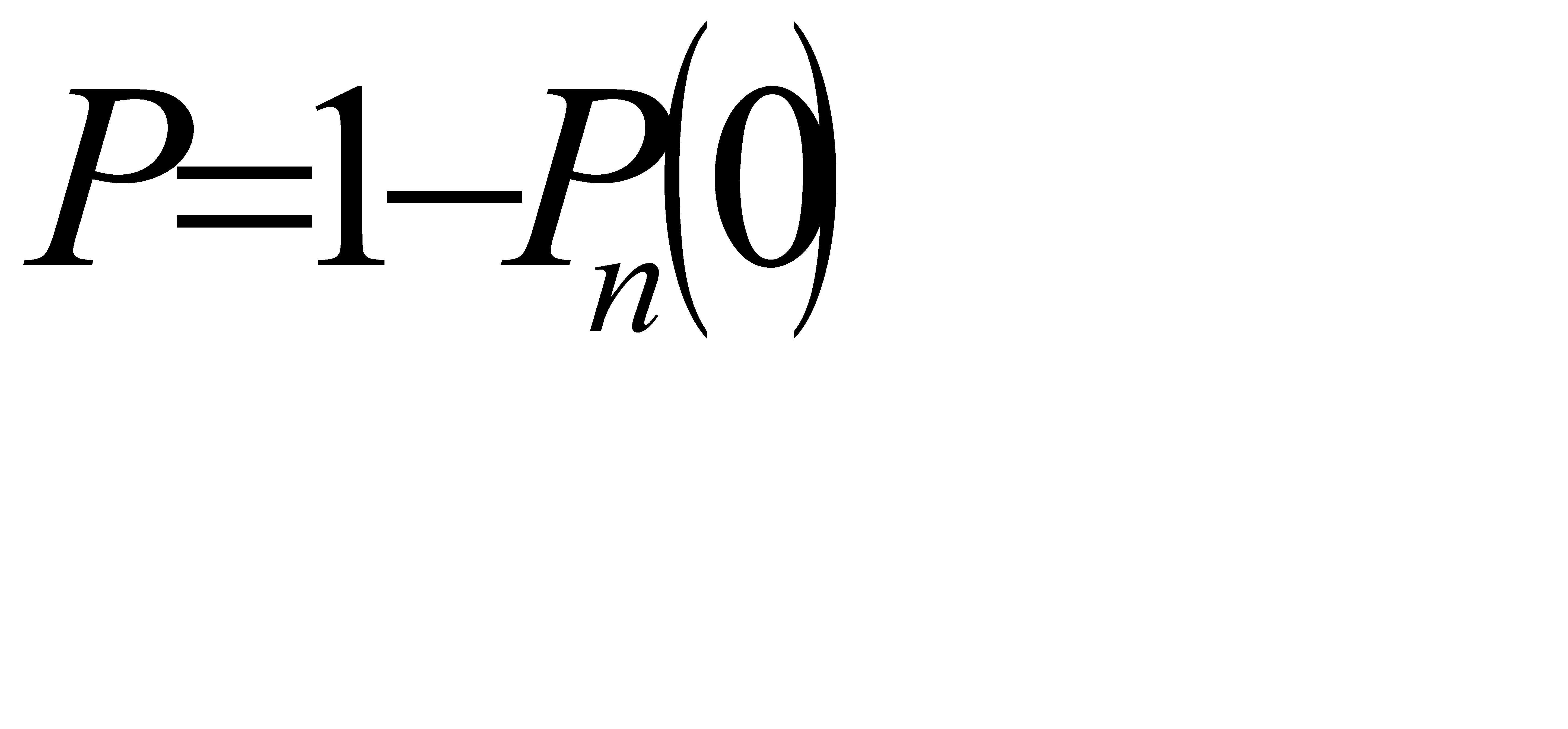 . (*)
. (*)
Положив 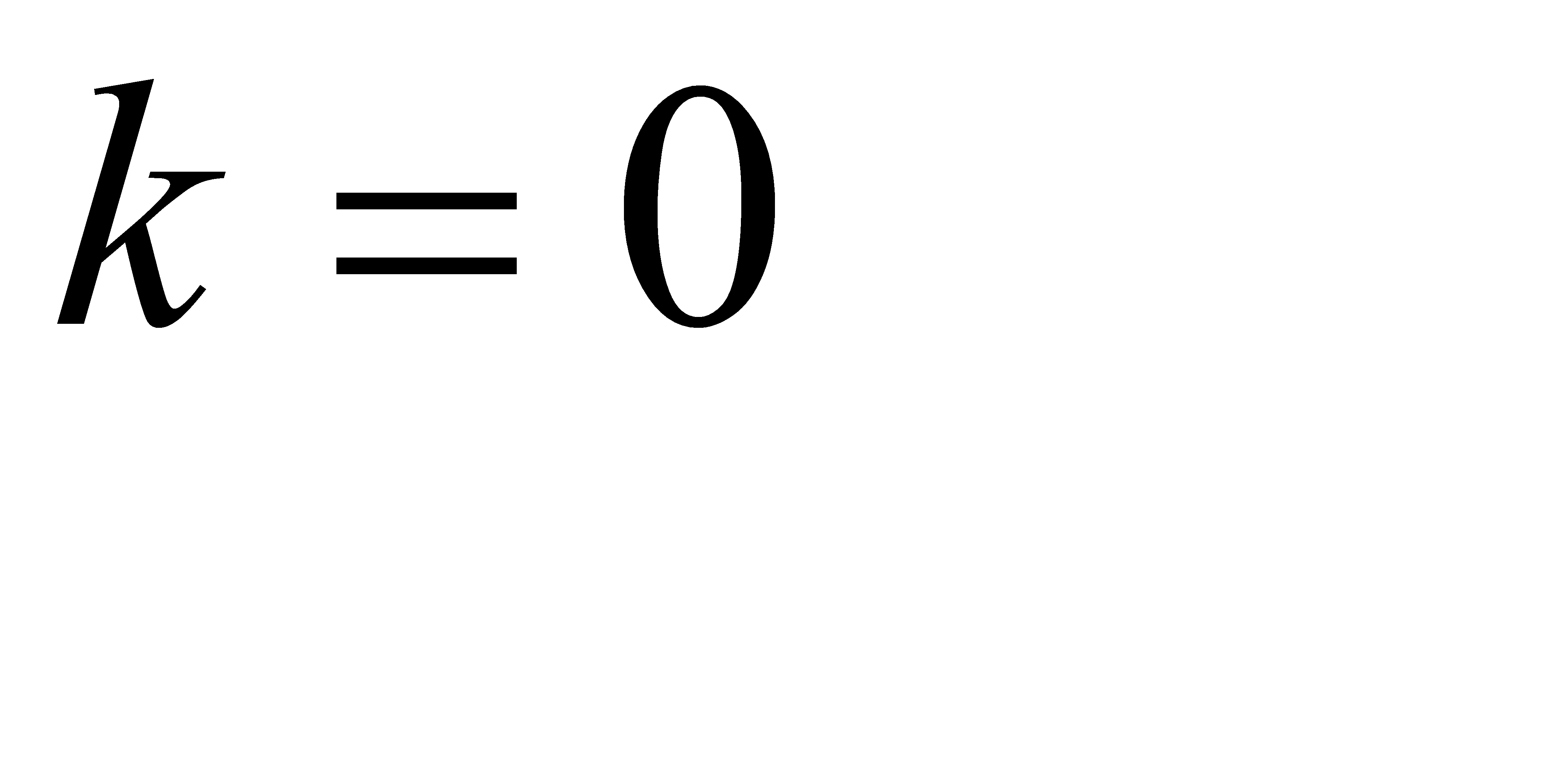 в формуле Пуассона
в формуле Пуассона 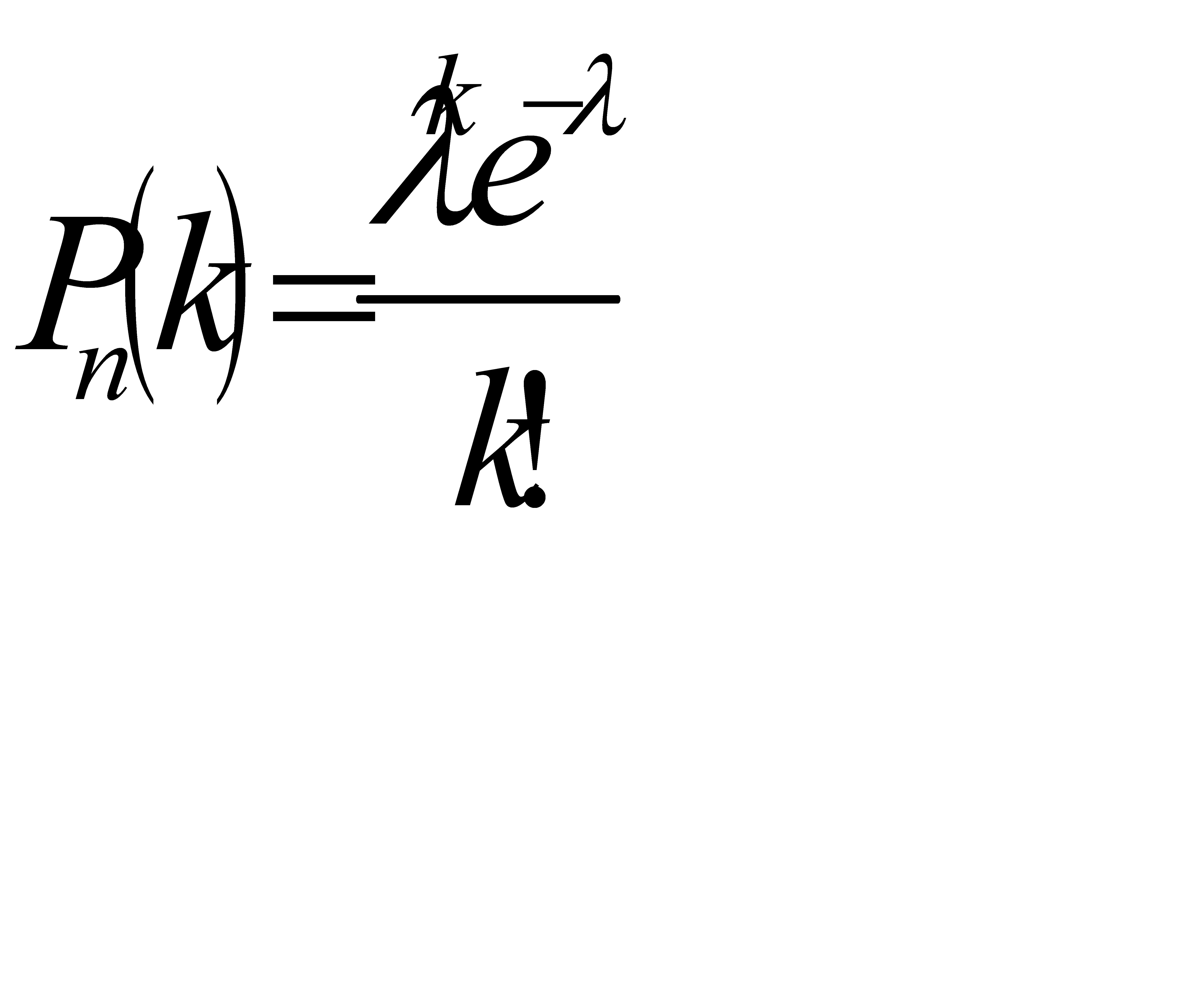 , получим
, получим 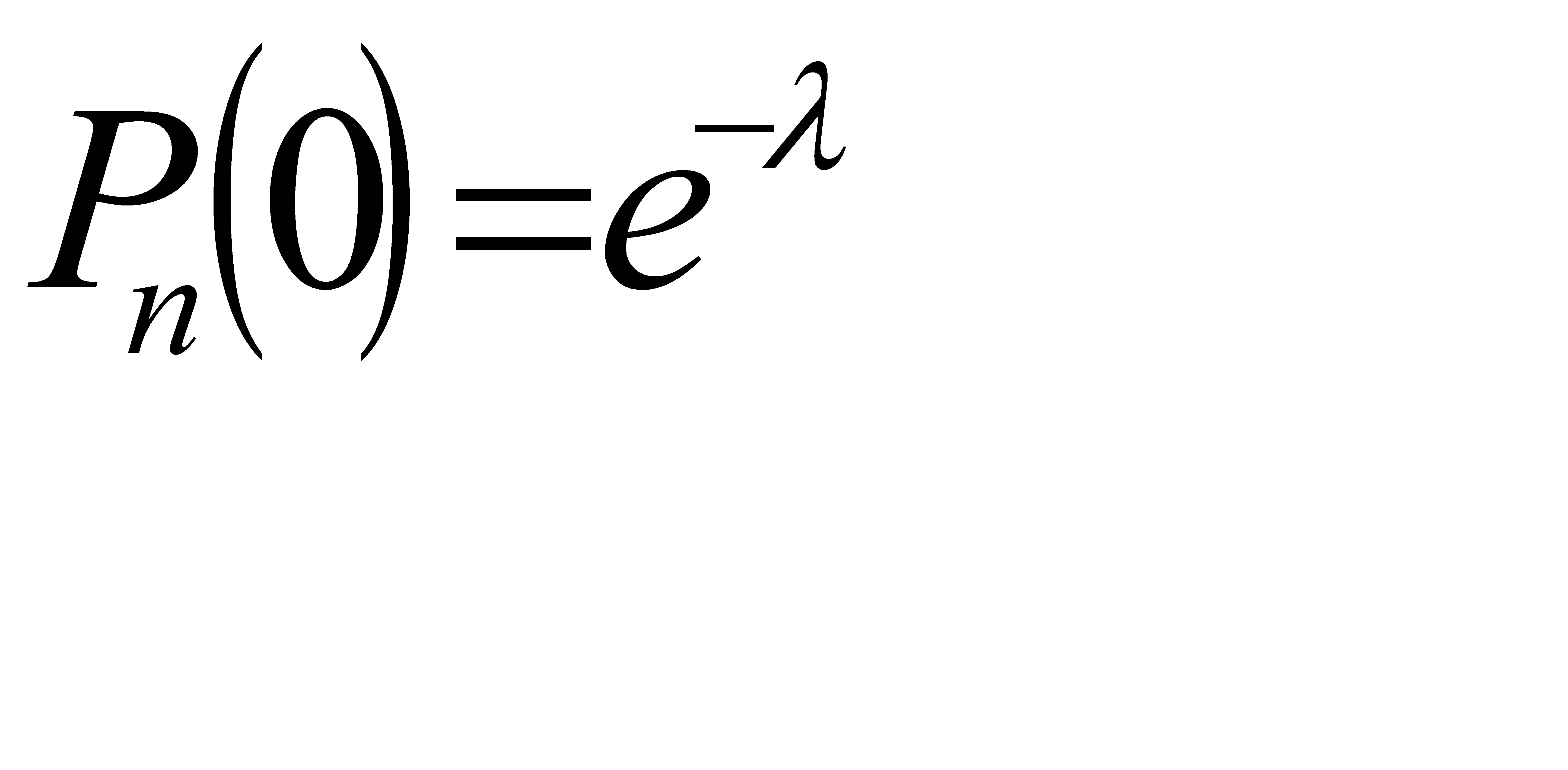
Следовательно, соотношение (*) примет вид 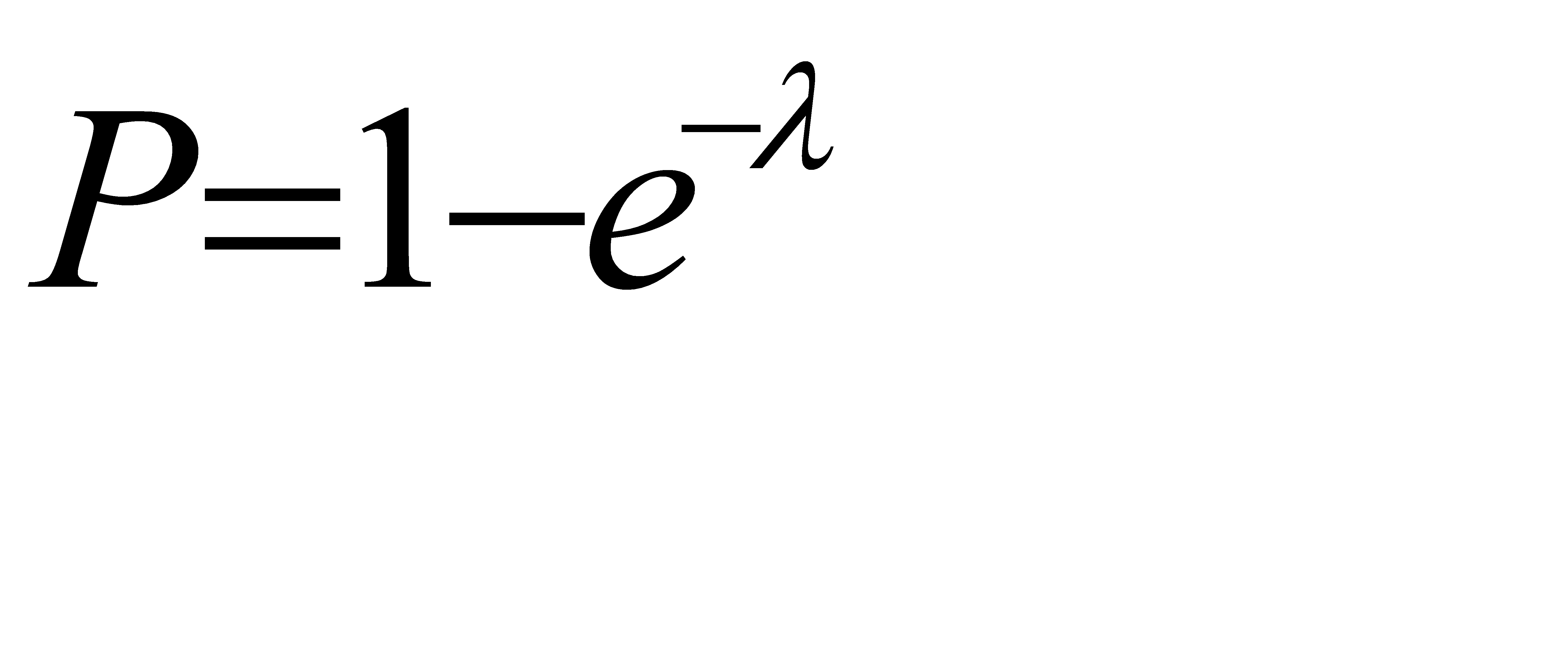 .
.
По условию, 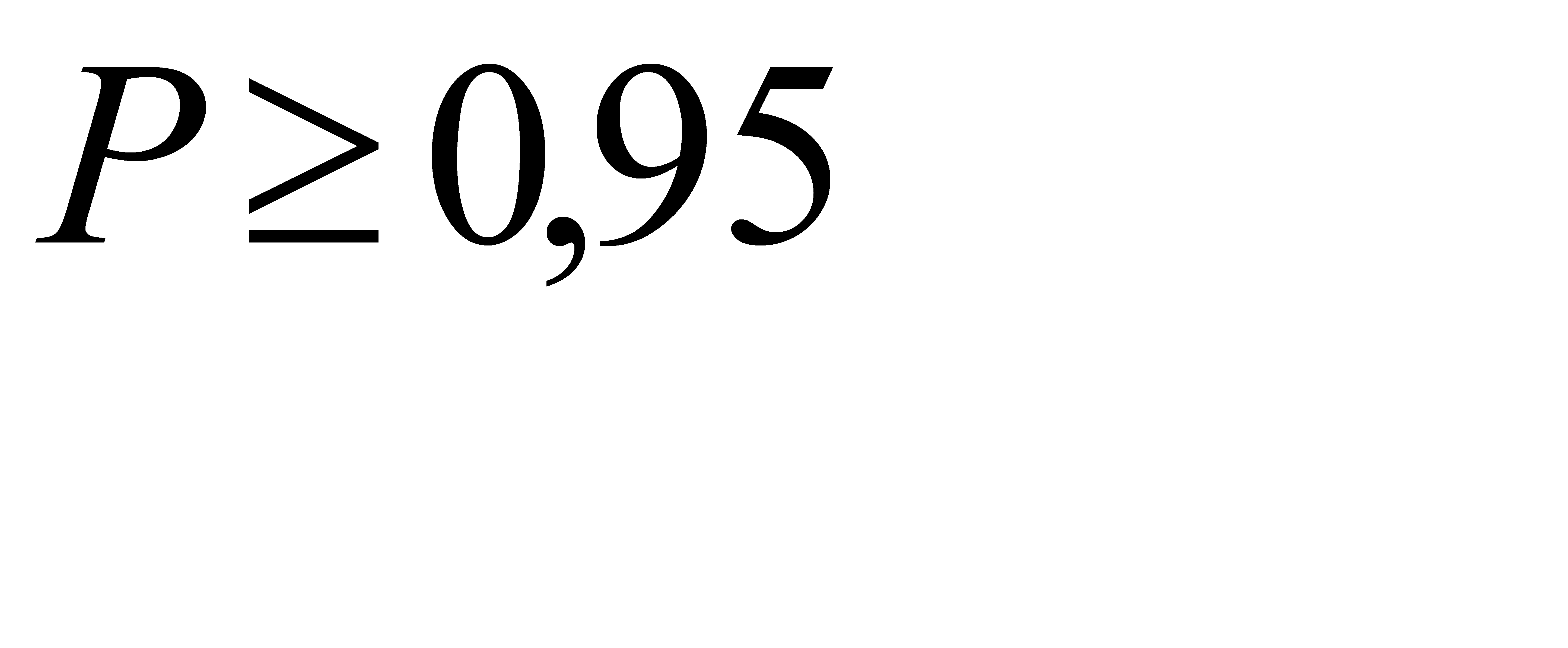 , или
, или 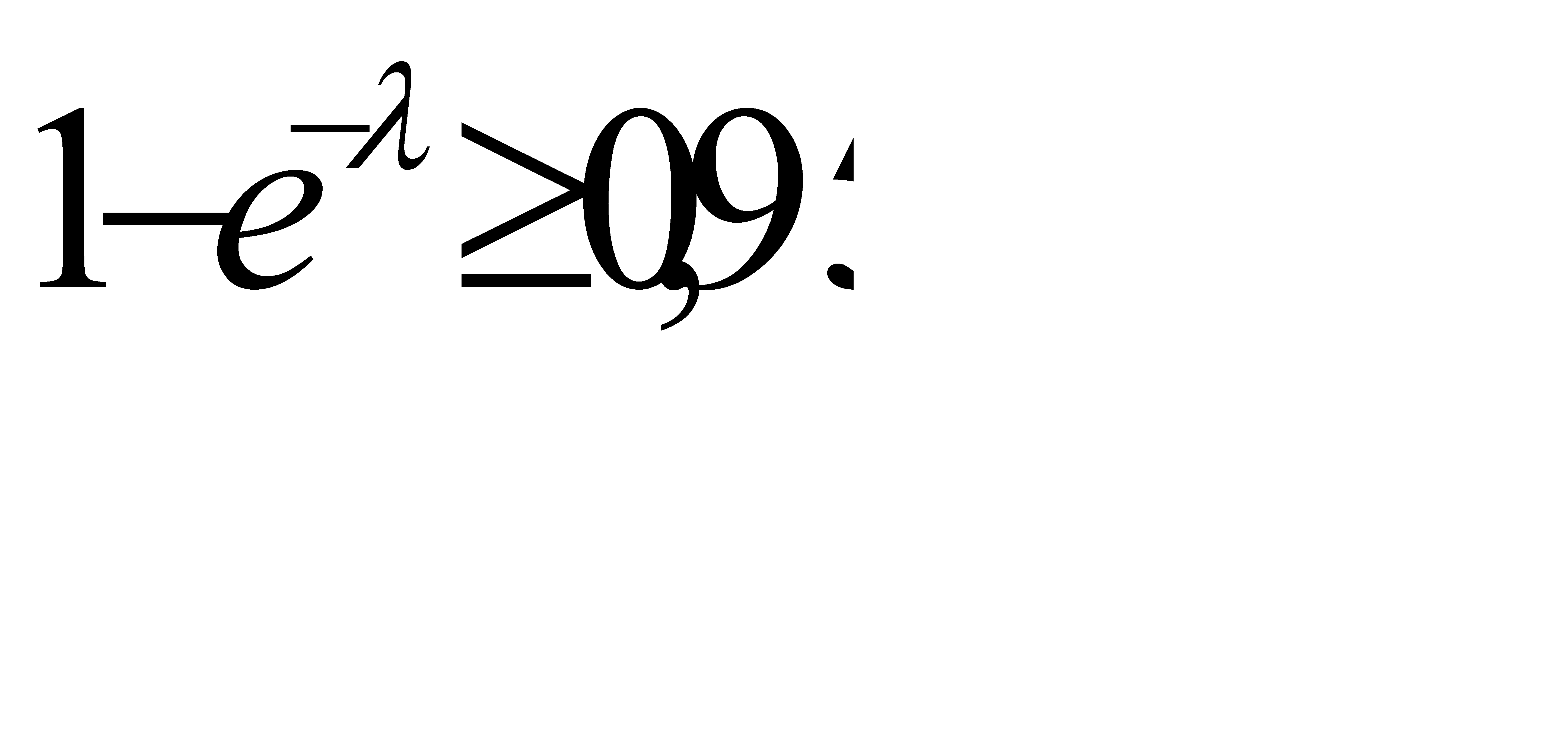 . Отсюда
. Отсюда 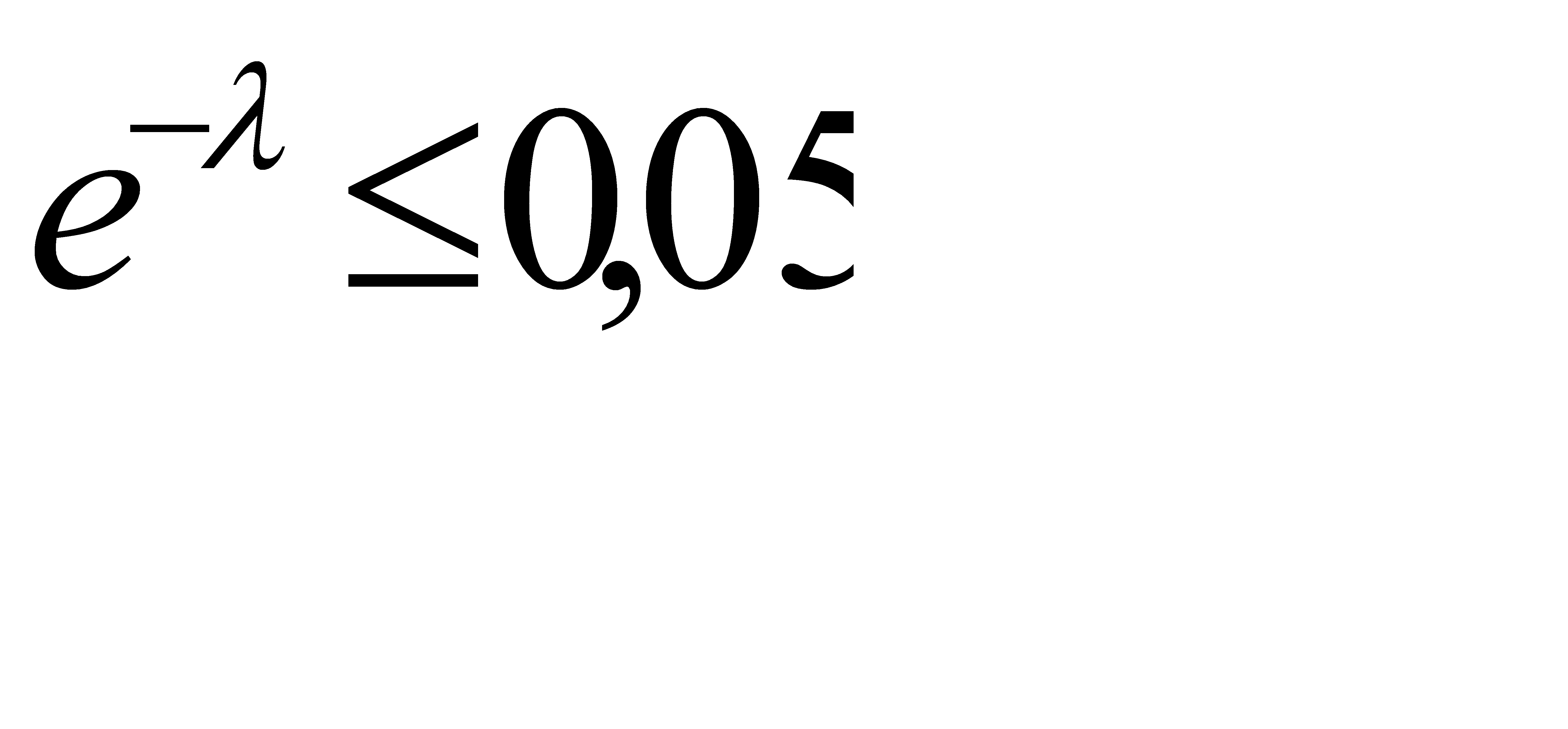 . (**)
. (**)
По таблице функции 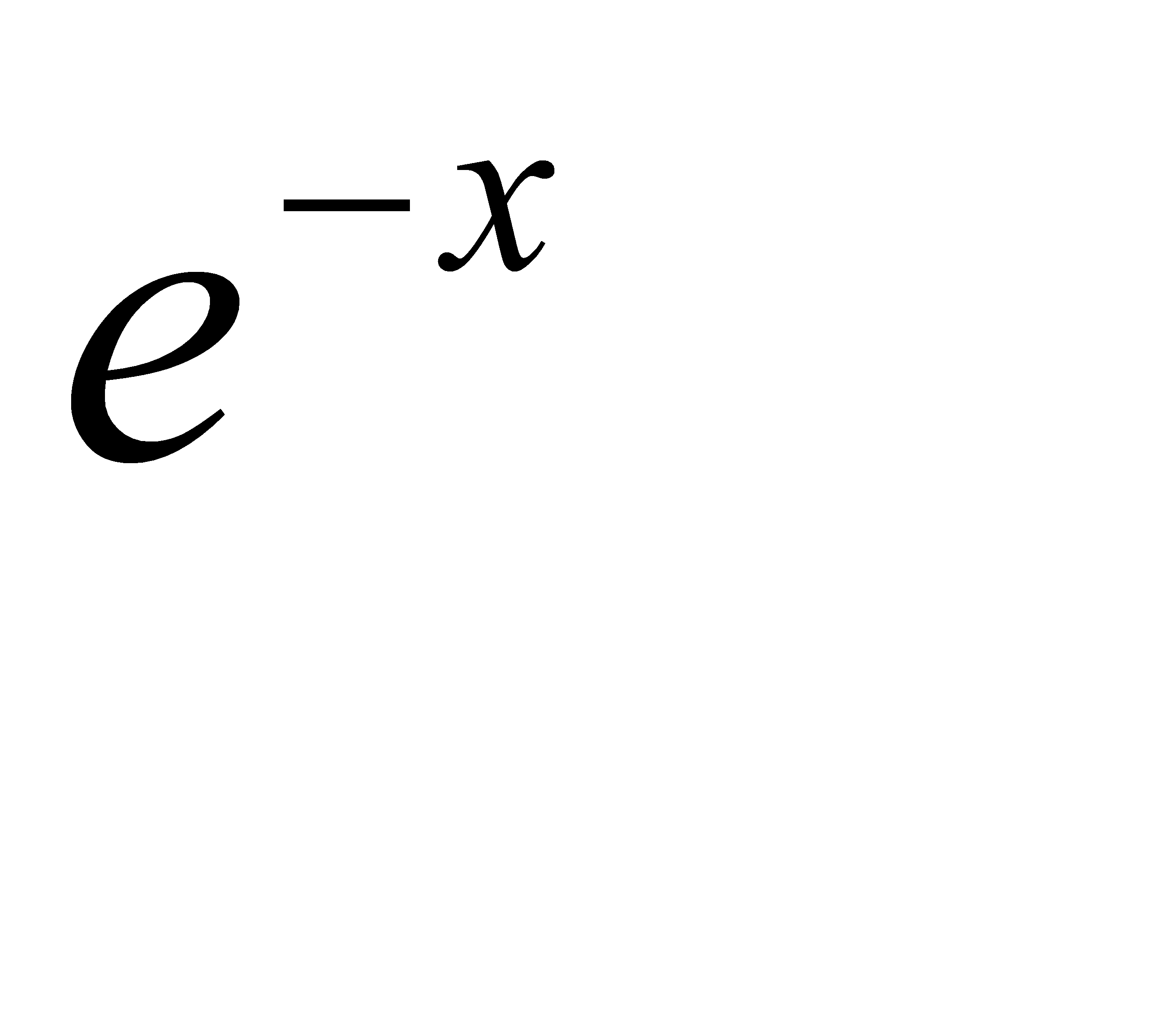 находим
находим 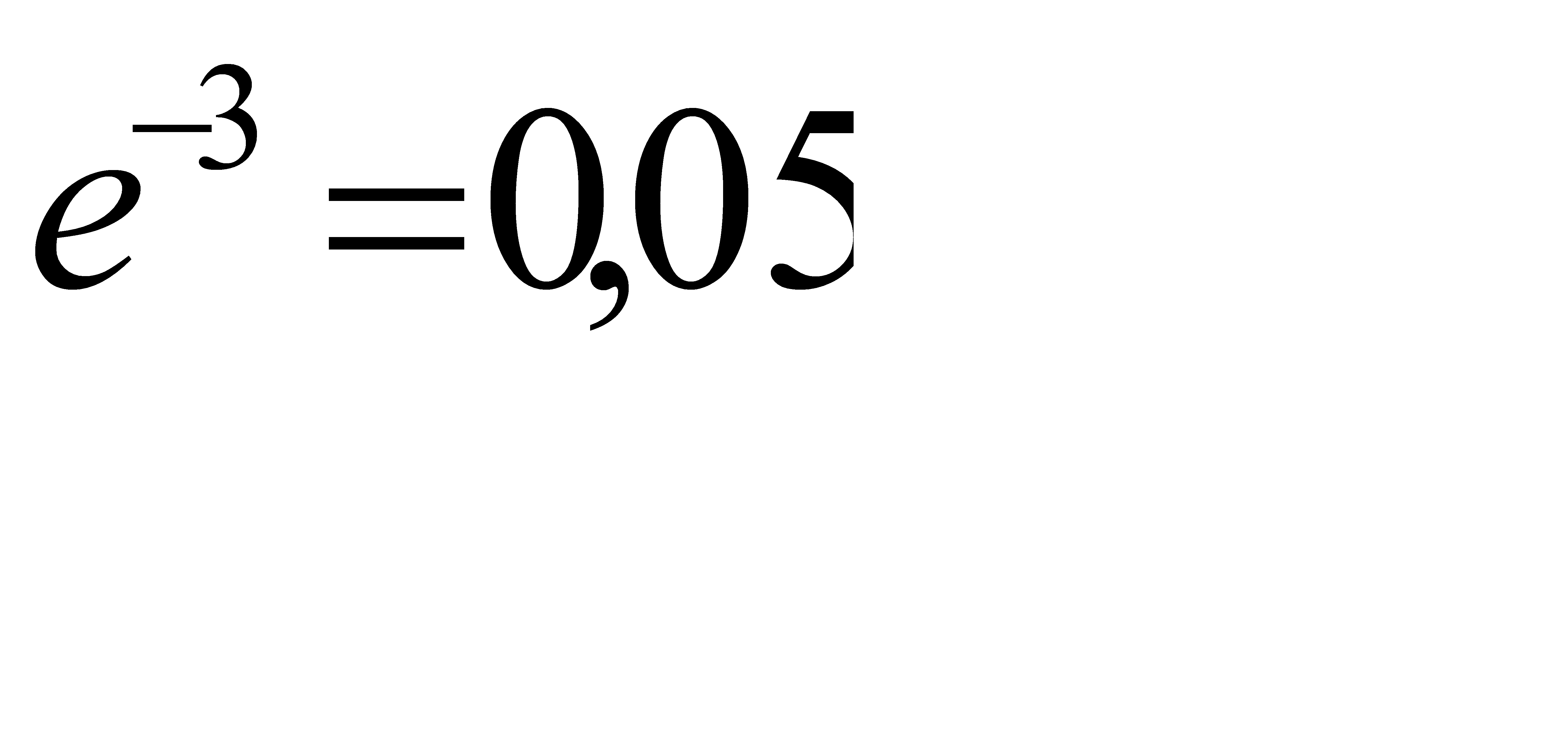 . Учитывая, что функция
. Учитывая, что функция 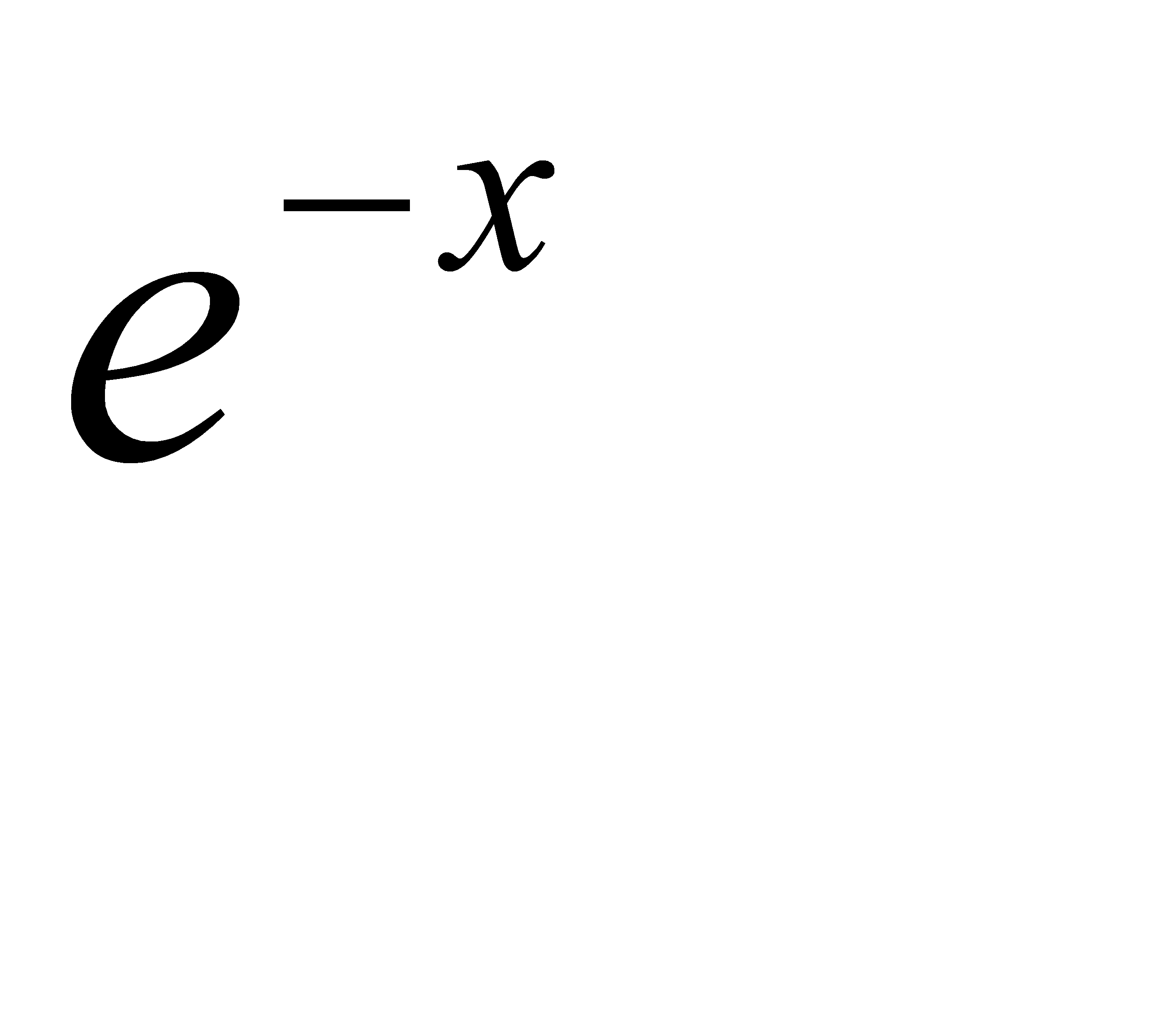 - убывающая, заключаем, что неравенство (**) выполняется при
- убывающая, заключаем, что неравенство (**) выполняется при 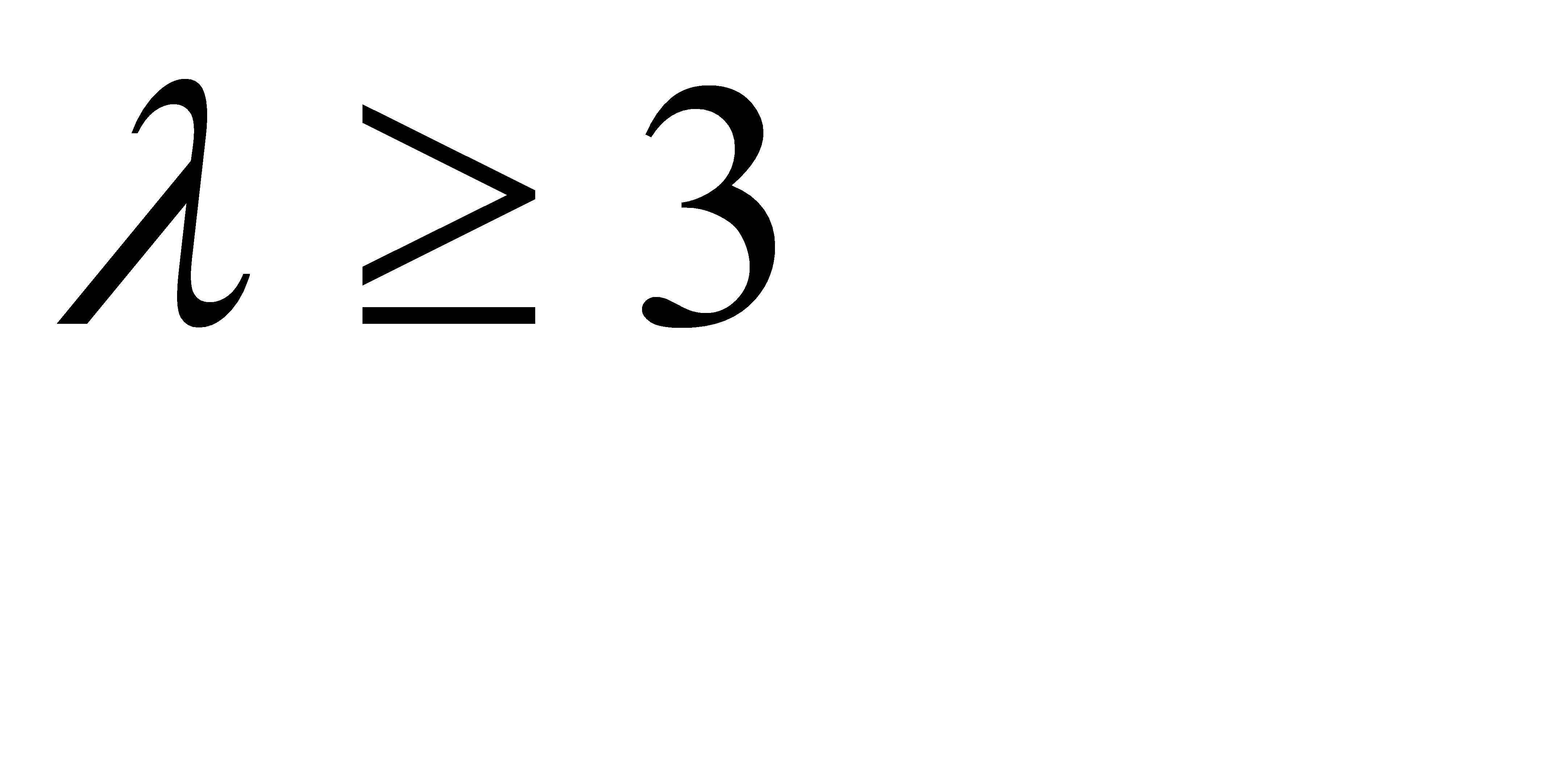 , или при
, или при 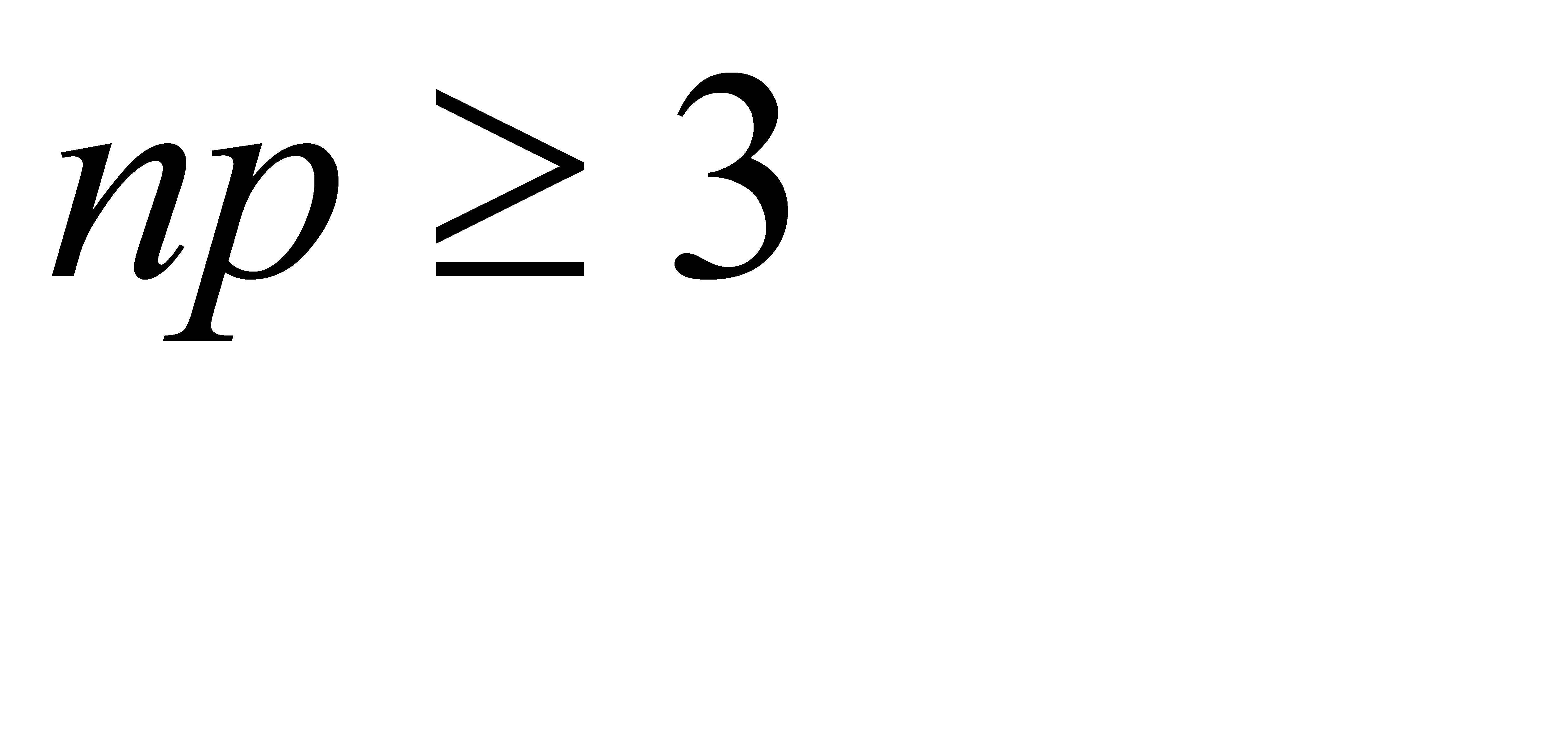 . Следовательно,
. Следовательно, 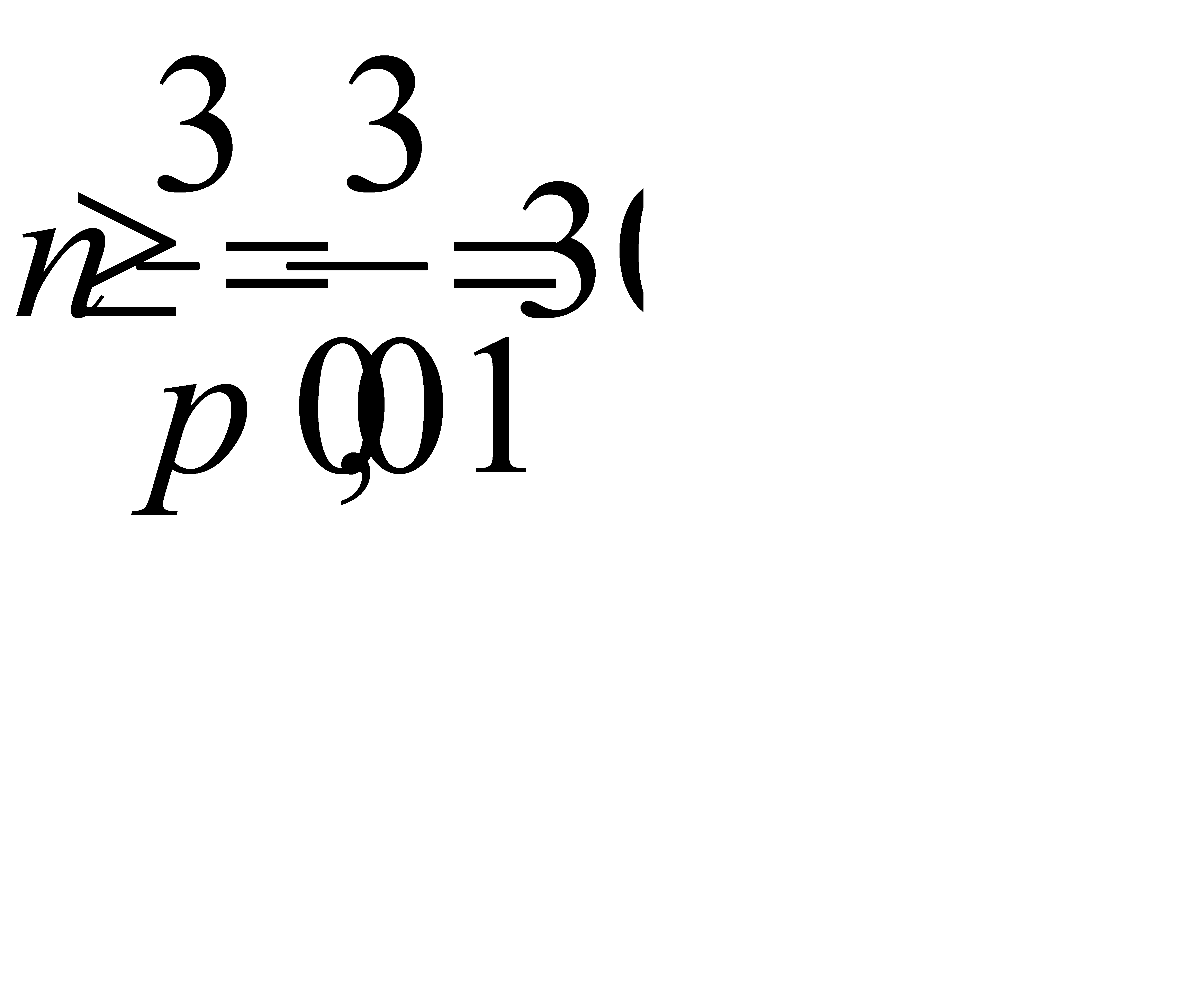 . Итак, надо купить не менее 300 билетов, чтобы выиграть хотя бы по одному из них.
. Итак, надо купить не менее 300 билетов, чтобы выиграть хотя бы по одному из них.
#184
Показать, что формулу Пуассона, определяющую вероятность появления k событий за время длительностью t
Pt(k)=( λ t)k*e-λ t/k! (*)
можно рассматривать как математическую модель простейшего потока событий; другими словами, показать, что формула Пуассона отражает все свойства простейшего потока.
Решение.
Из формулы (*) видно, что вероятность появления k событий за время длительностью t, при заданной интенсивности λ, является функцией только k и t, что отражает свойство стационарности простейшего потока.
Формула (*) не использует информации о появлении событий до начала рассматриваемого промежутка времени, что отражает свойство отсутствия последействия.
Покажем, что формула отражает свойство ординарности. Положив k=0 и k=1, найдем вероятность непоявления событий и вероятность появления одного события:
Pt(0)= e-λ t, Pt(1)= λ te-λ t.
Следовательно, вероятность появления более одного события
Pt(k> 1)=1-[ Pt(0)+ Pt(1)]=1-[e-λ t+ λ te-λ t]
Используя разложение функции e-λ t в ряд Маклорена, после элементарных преобразований получим
Pt(k> 1)=(λ t)2/2+….
Сравнивая Pt (1) и Pt(k> 1), получаем, что при малых значениях t вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью наступления одного события, что отражает свойство ординарности.
Ч. Т. Д.
#185
Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно трем. Найти вероятность того, что за 2 мин поступит: а) четыре вызова; б) менее четырех вызовов; в) не менее четырех вызовов.
Решение: По условию λ =3, t=2, k=4. Воспользуемся формулой Пуассона:
Ptk=λ tke-λ tk!.
a) Искомая вероятность того, что за 2 мин поступит 4 вызова:
P24=64e-64! =1296*0, 002524=0, 135.
б) Событие “поступило менее четырех вызовов” произойдет, если наступит одно из следующих несовместных событий: 1) поступило три вызова; 2) поступило два вызова; 3) поступил один вызов; 4) не поступило ни одного вызова. Эти события несовместны, поэтому применимая теорема сложения вероятностей несовместных событий:
P2k< 4=P23+P22+P21+P20=63e-63! +62e-62! +6e-61! +e-6=e-636+18+6+1=0, 0025*61=0, 1525.
в) События “поступило менее четырех вызовов” и “поступило не менее четырех вызовов” противоположны, поэтому искомая вероятность того, что за 2 мин поступит не менее четырех вызовов:
Pk≥ 4=1-Pk< 4=1-0, 1525=0, 8475.
#186
По условию, λ =2, t=4, k=3
Воспользуемся формулой Пуассона
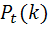 =
= 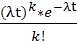
а)вероятность того, что за 4 минуты поступит 3 вызова
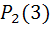 =
= 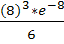 =0. 0256
=0. 0256
б)Событие “поступило менее 3-х вызовов” произойдет, если поступит одно из несовместных событий: поступило 2 вызова или поступил 1 вызов или вызовов не поступило
Эти события несовместны, поэтому применима теорема сложения вероятностей несовместных событий:
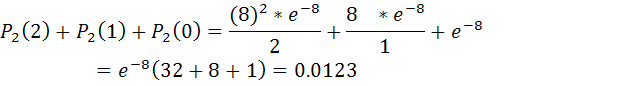
в)События “поступило менее 3-х вызовов” и “поступило не менее 3-х вызовов” противоположны, поэтому искомая вероятность того, что за 4 минуты поступит не менее 3-х вызовов:
P(k≥ 3)=1-P(k< 3)=1-0. 0123=0. 9877
#187
Доказать, что для простейшего потока событий
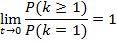
Решение: Воспользуемся теоремой о сумме вероятностей противоположных событий: 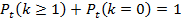
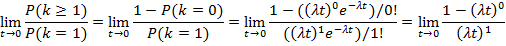
Применяя правило Лопиталя получим
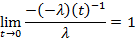
Ч. Т. Д.
#188
Найти математическое ожидание дискретной случайной величины X, заданной законом распределения:
а)
| X | -4 | ||
| p | 0, 2 | 0, 3 | 0, 5 |
б)
| X | 0, 21 | 0, 54 | 0, 61 |
| P | 0, 1 | 0, 5 | 0, 4 |
Решение.
а) Математическое ожидание равно сумме произведений всех возможных значений 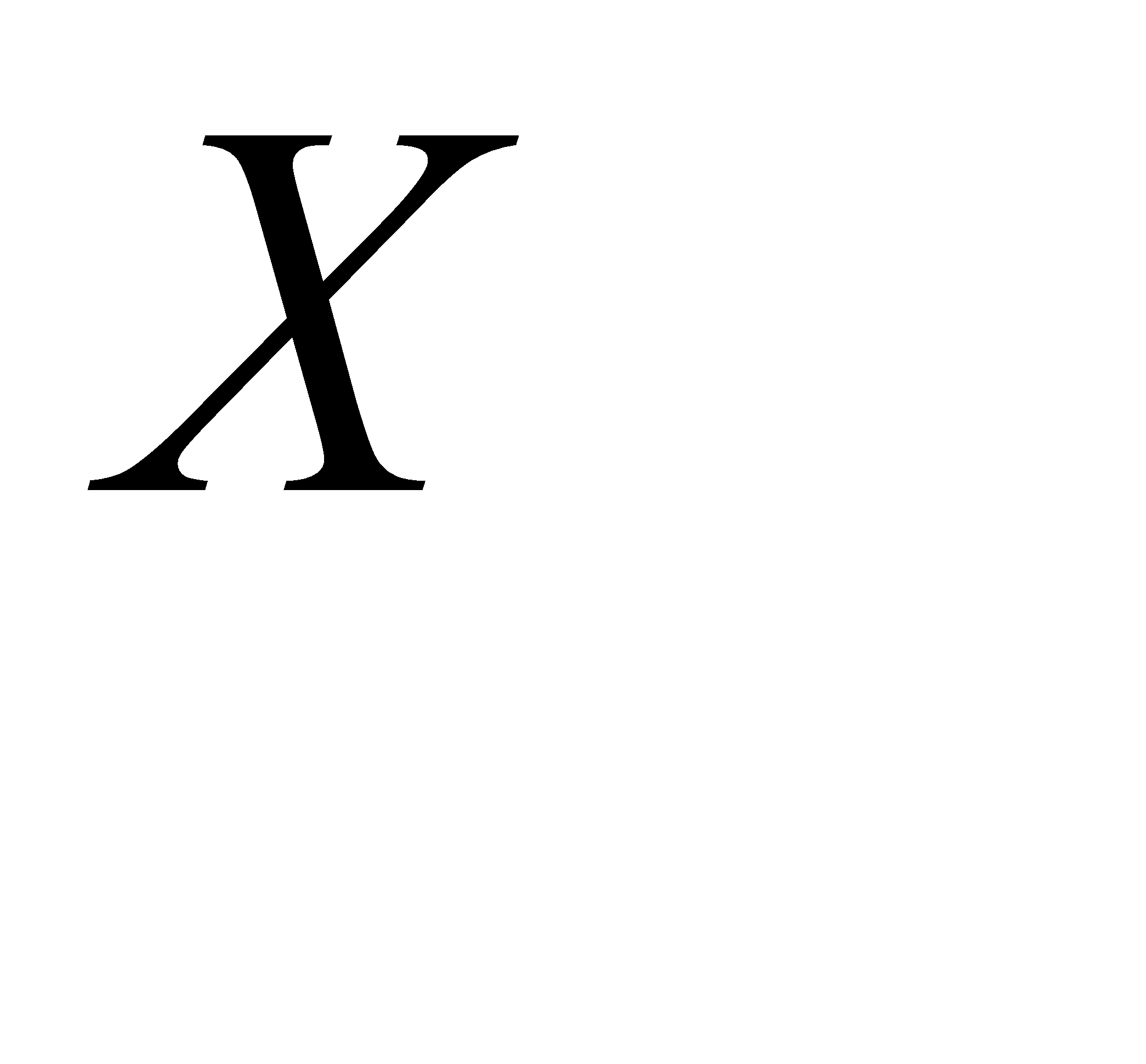 на их вероятности:
на их вероятности:
 .
.
б)  .
.
#189
Найти математическое ожидание случайной вели-
величины Z, если известны математические ожидания X и Y:
a) Z = X + 2Y, Af(X) = 5, M(Y) = 3; б) Z = 3X+4Y,
Af(X) = 2, M(Y) = 6.
Решение, а) Используя свойства математического ожидания
(математическое ожидание суммы равно сумме математических ожи-
ожиданий слагаемых; постоянный множитель можно вынести за знак
математического ожидания), получим
М (Z) = М (X + 2К) = М (X) + М BY) = М (X)+2М (К) =
=5+2-3=11.
#190
Используя свойства математического ожидания, доказать, что: а) 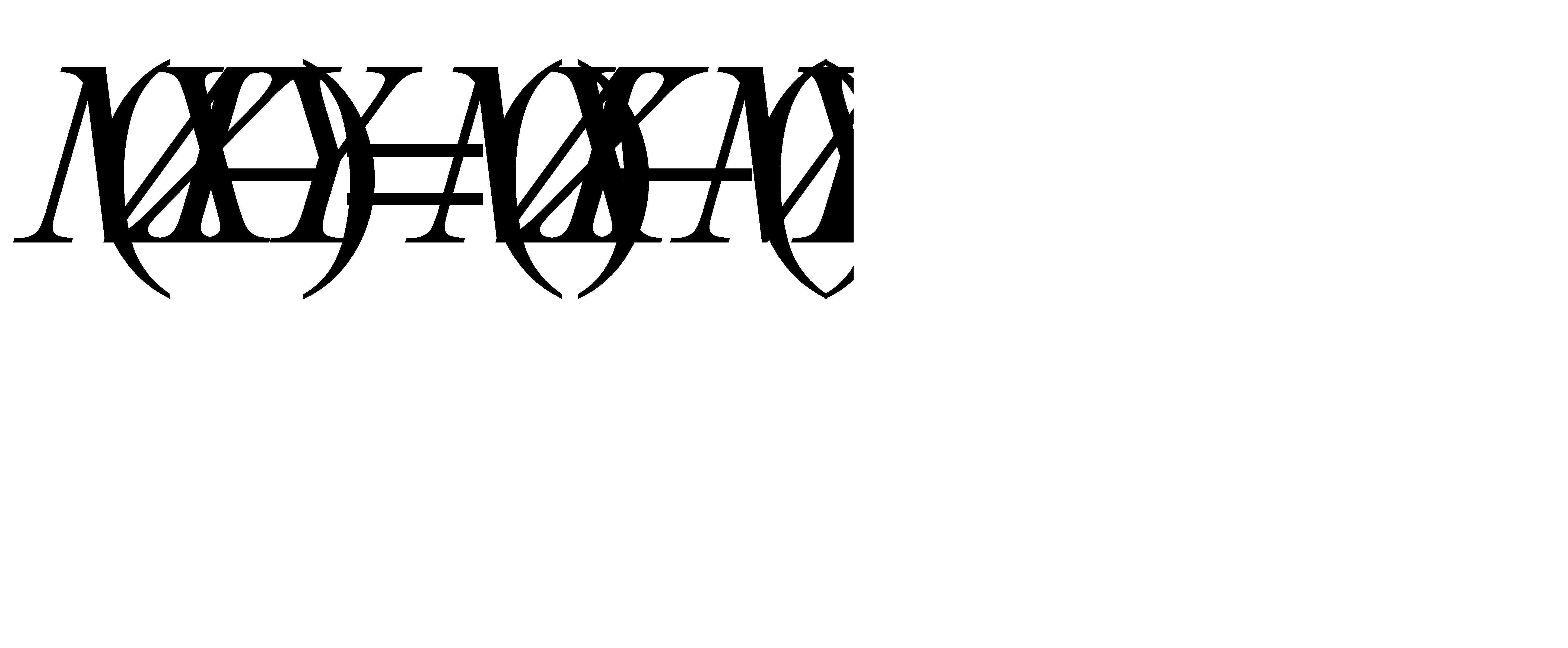 , б) математическое ожидание отклонения
, б) математическое ожидание отклонения 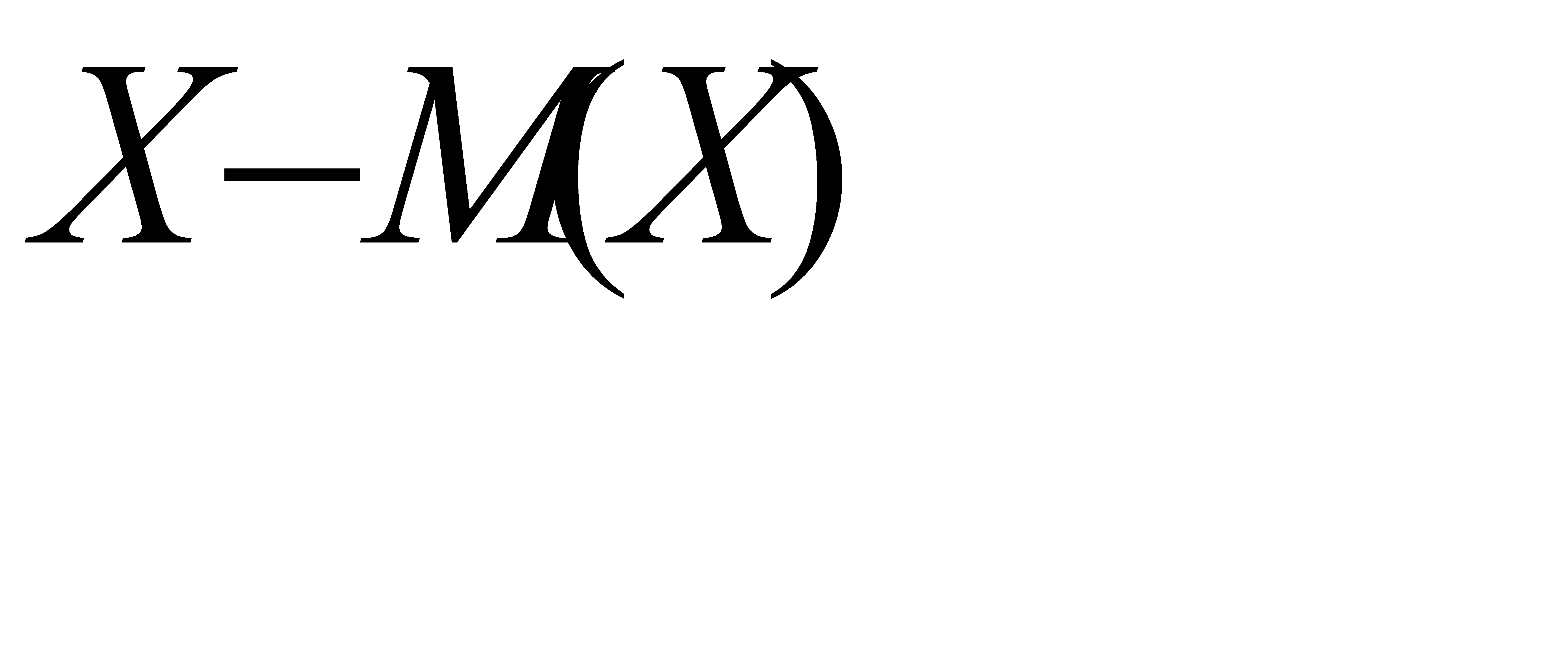 равно нулю.
равно нулю.
Решение.
а) Положим 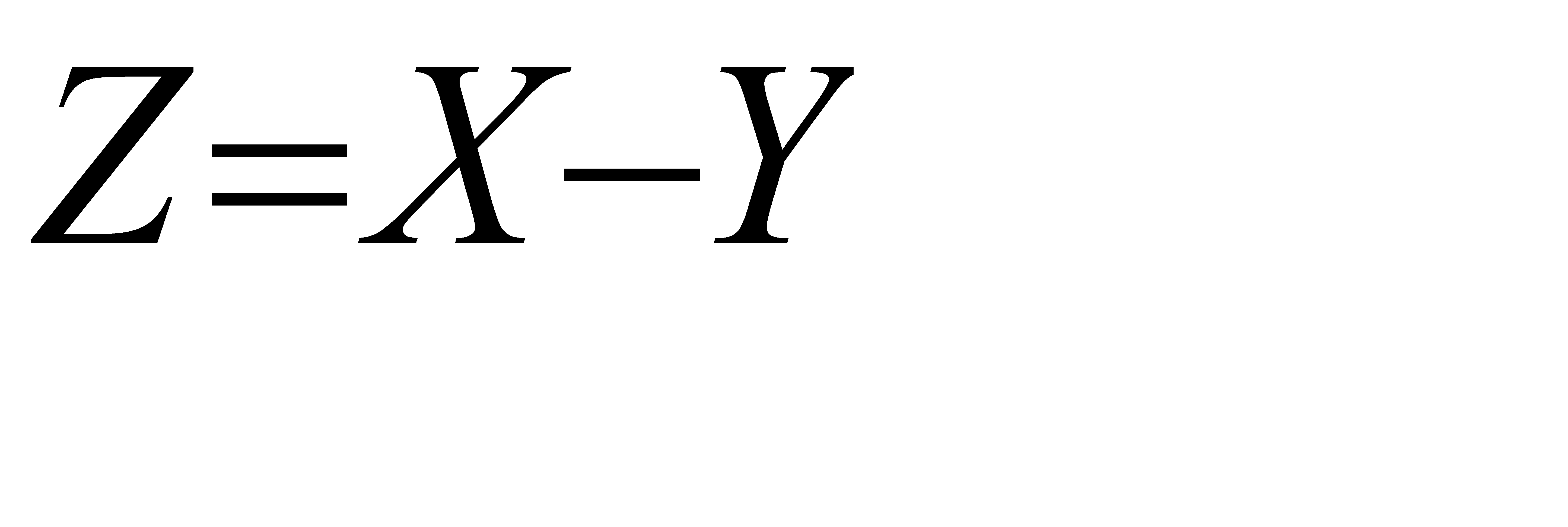 . Тогда
. Тогда 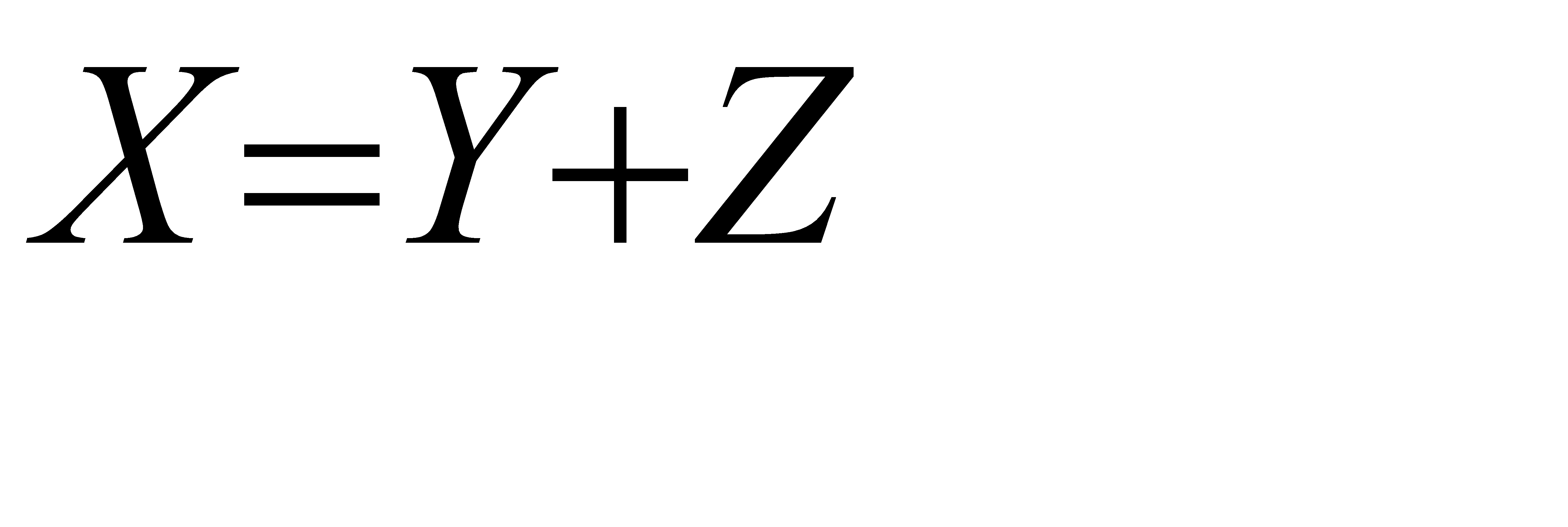 . Из свойства 4 математического ожидания следует, что
. Из свойства 4 математического ожидания следует, что 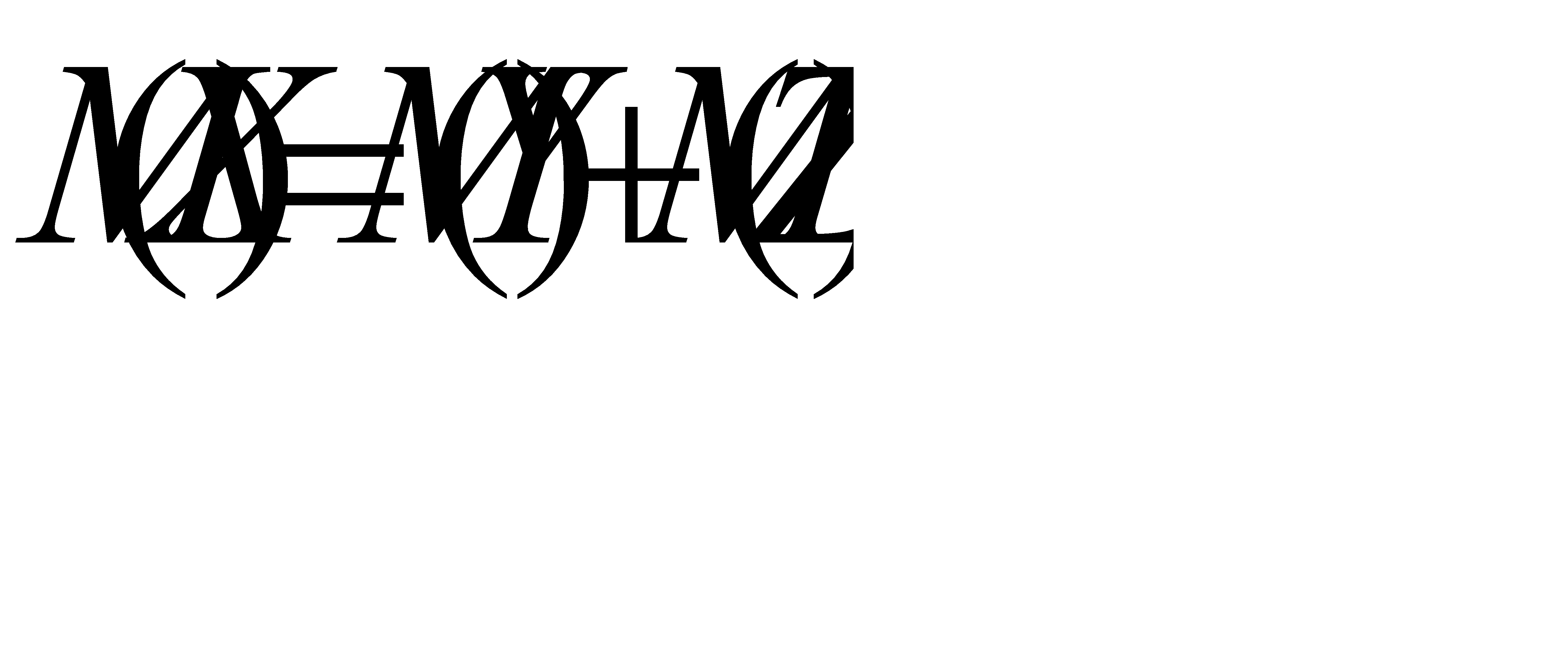 . Отсюда
. Отсюда 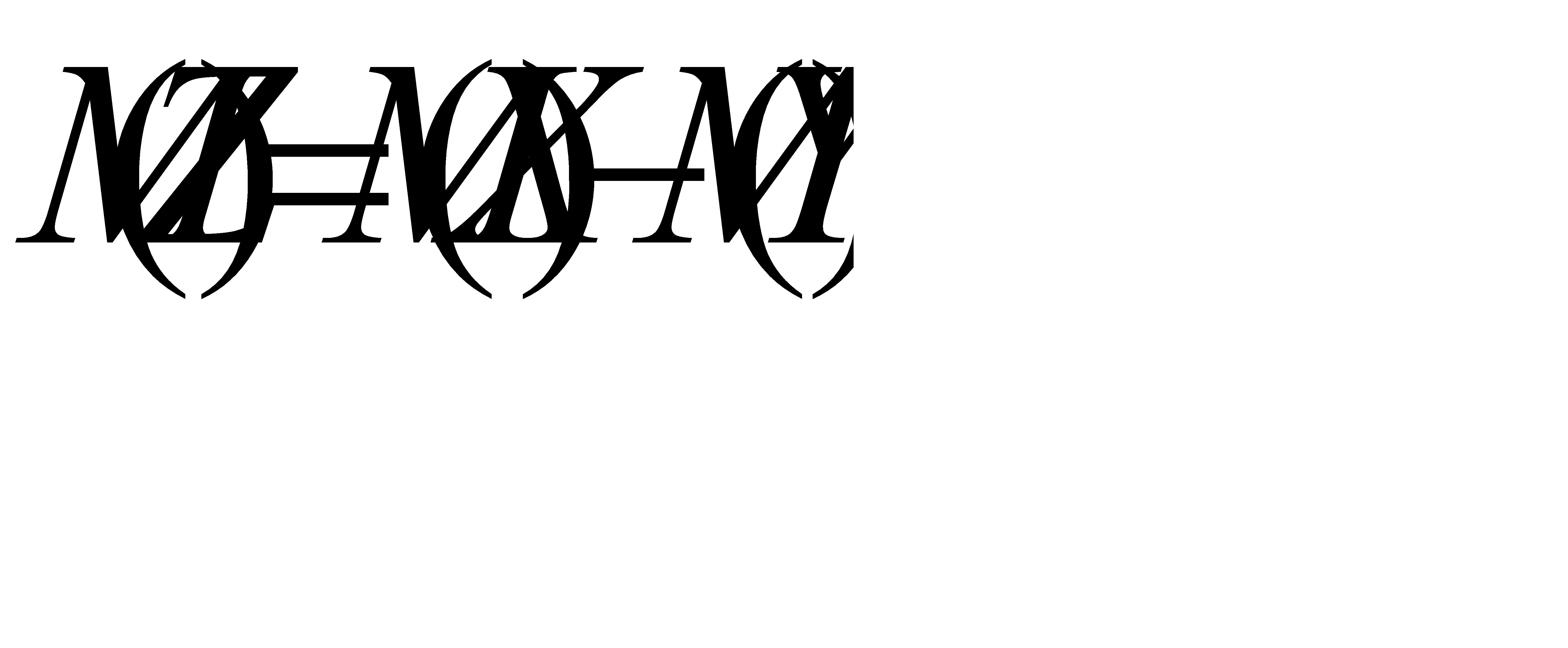 .
.
Но так как 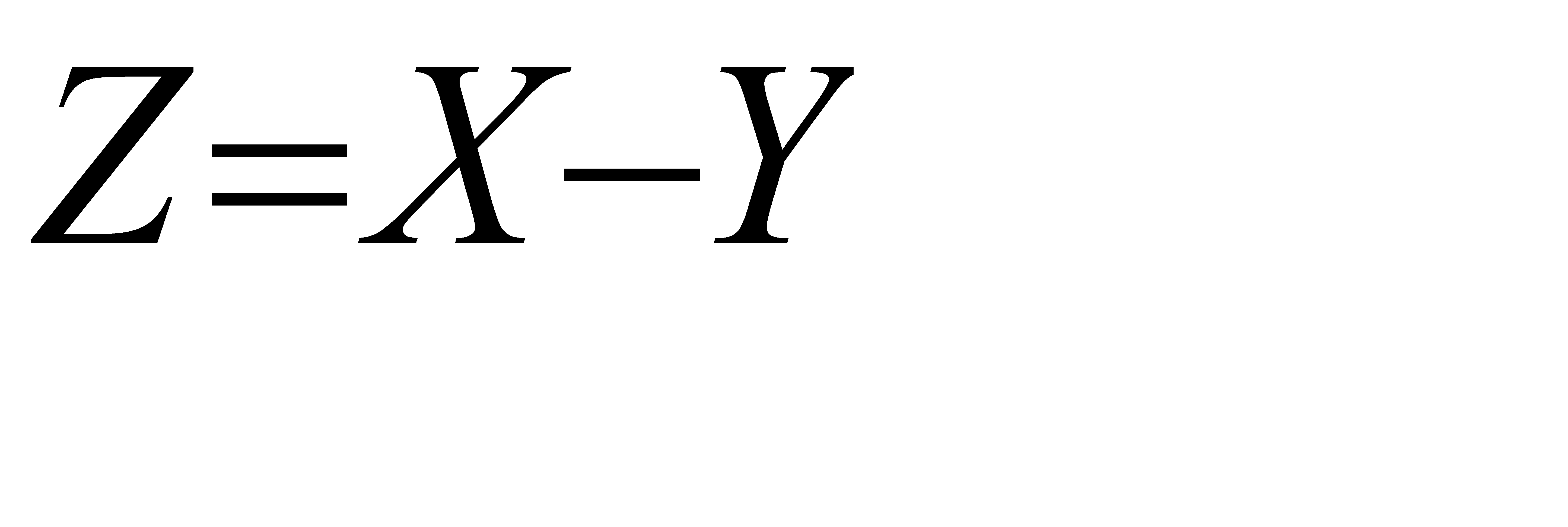 , имеем
, имеем
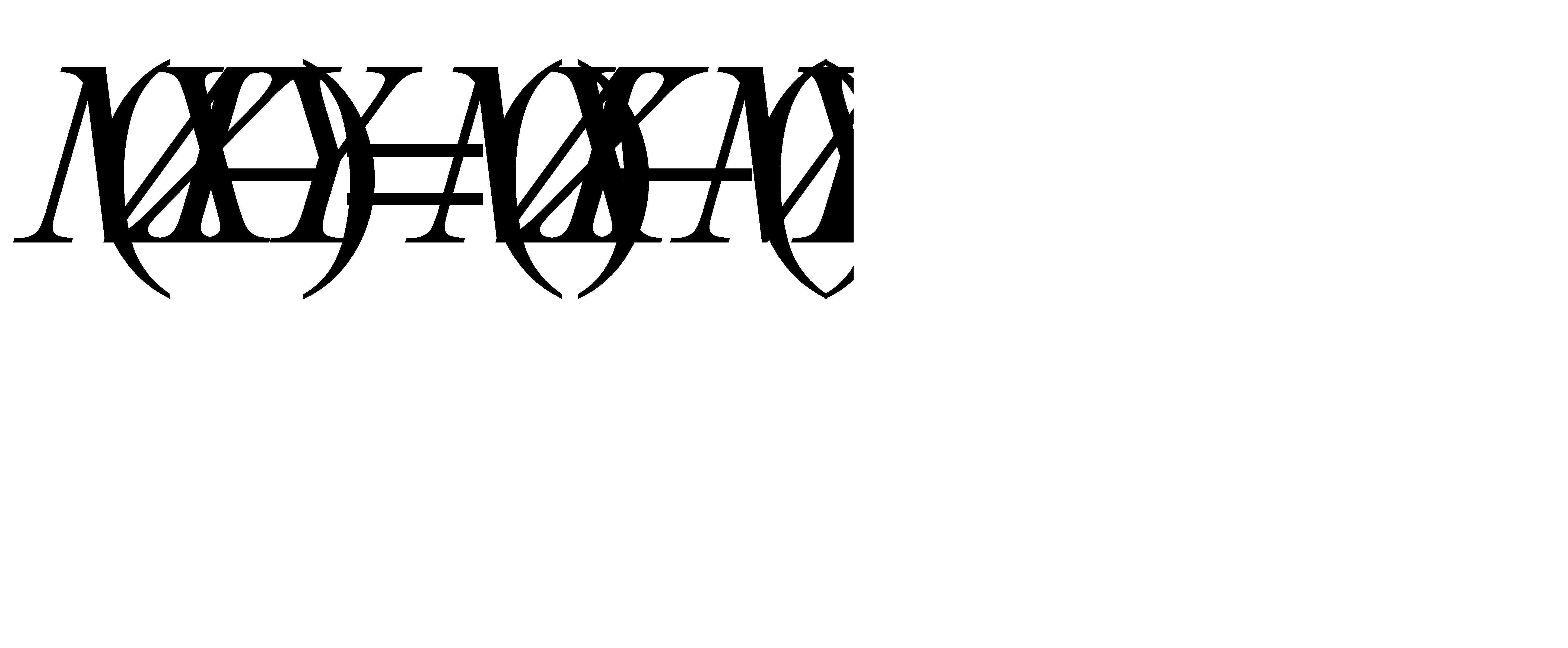 , что и требовалось доказать.
, что и требовалось доказать.
б) Требуется доказать, что верно равенство 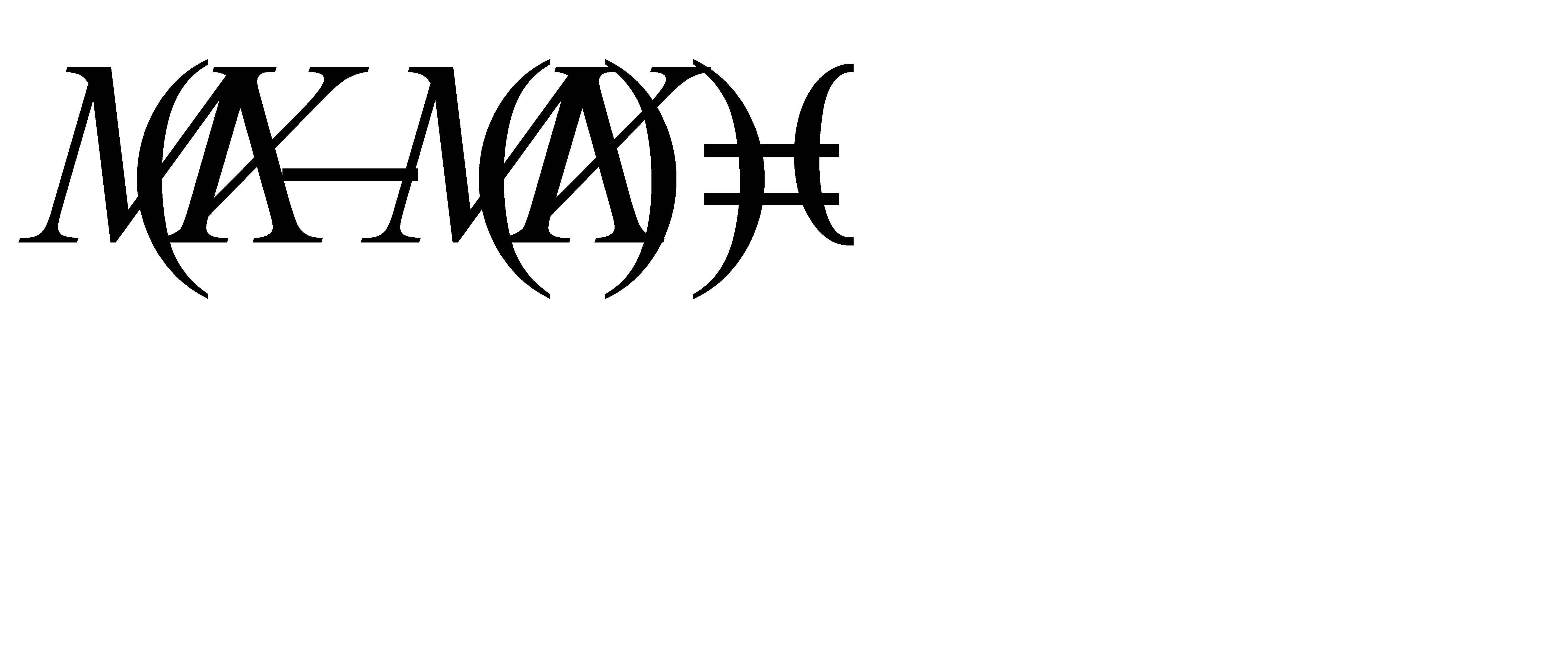 . По формуле, доказанной в п. а), получаем
. По формуле, доказанной в п. а), получаем  .
.
Так как математическое ожидание 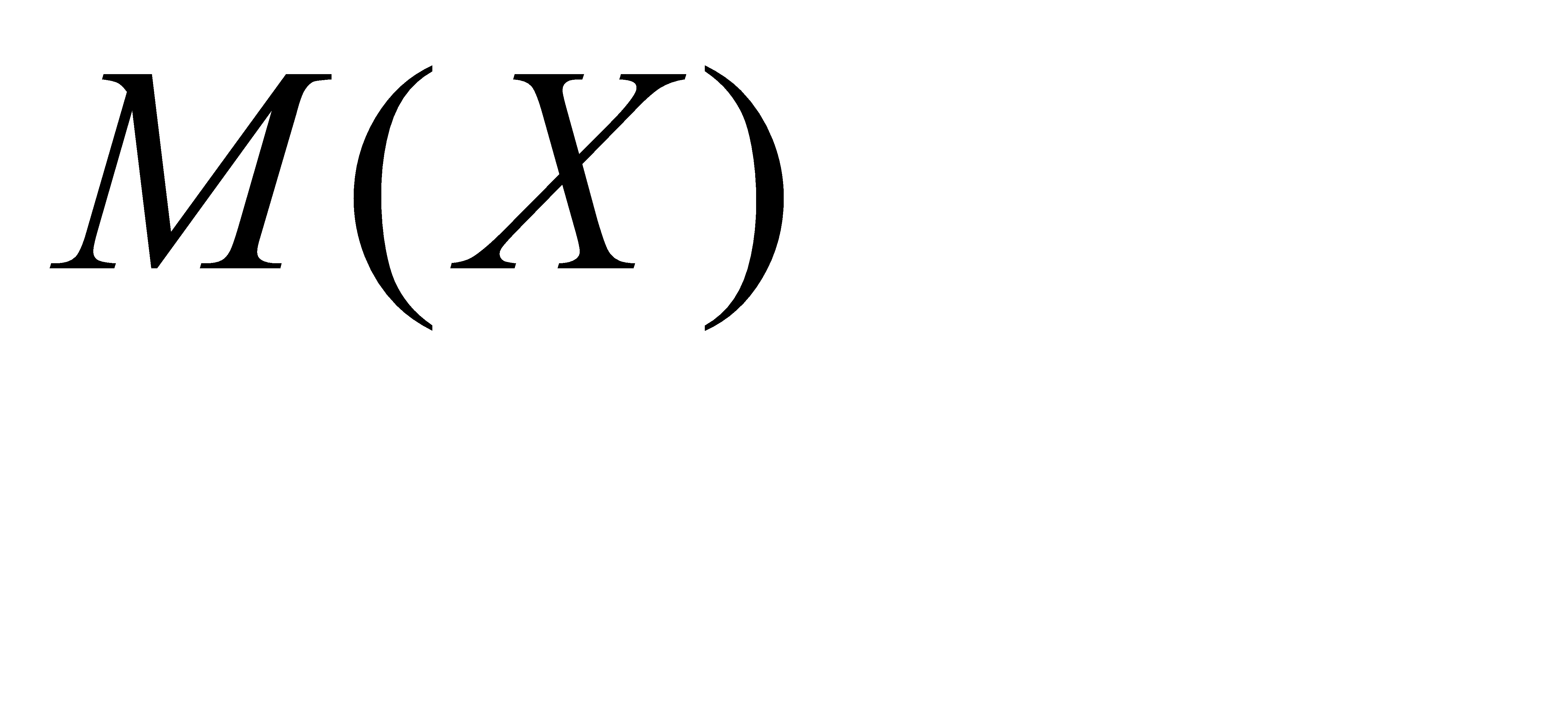 есть постоянная, можно воспользоваться свойства 1 случайной величины:
есть постоянная, можно воспользоваться свойства 1 случайной величины: 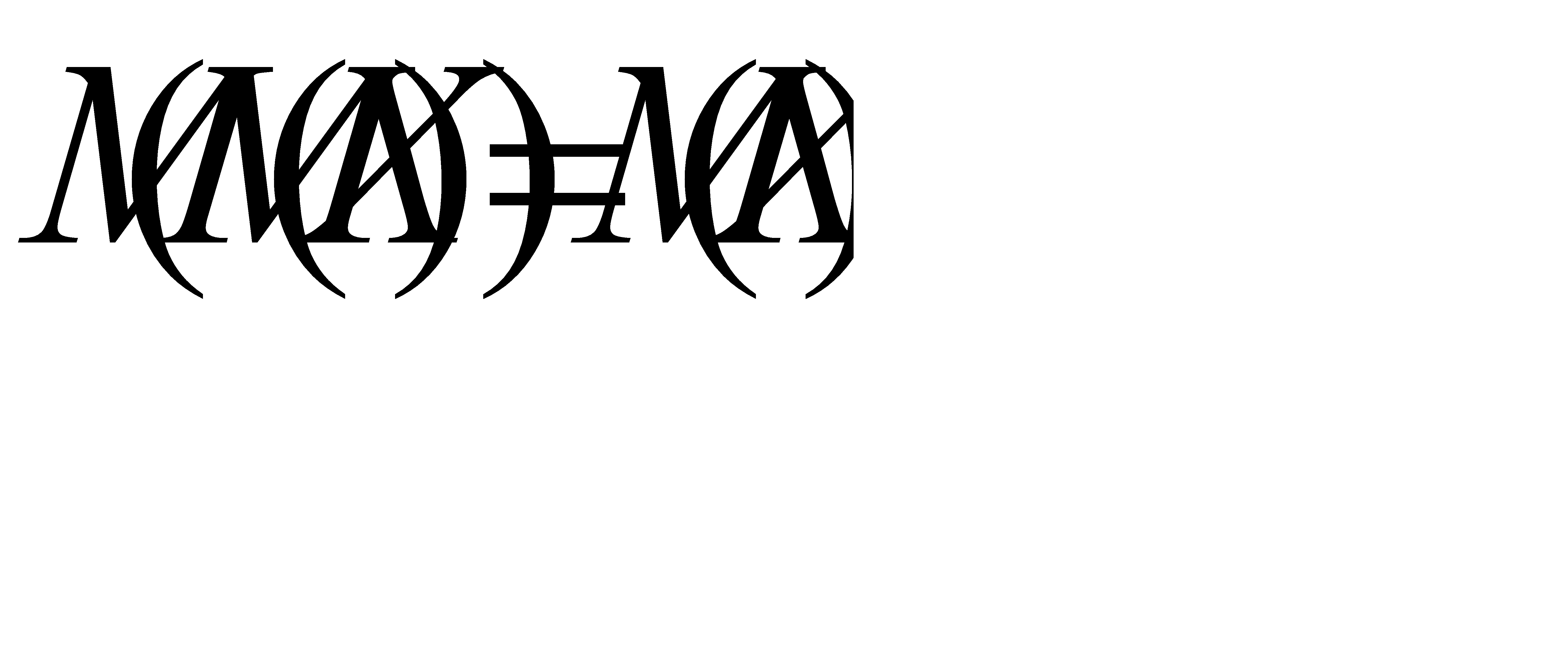 . Теперь имеем
. Теперь имеем
 , что и требовалось доказать.
, что и требовалось доказать.
#191
Дискретная случайная величина X принимает три возможных значения: 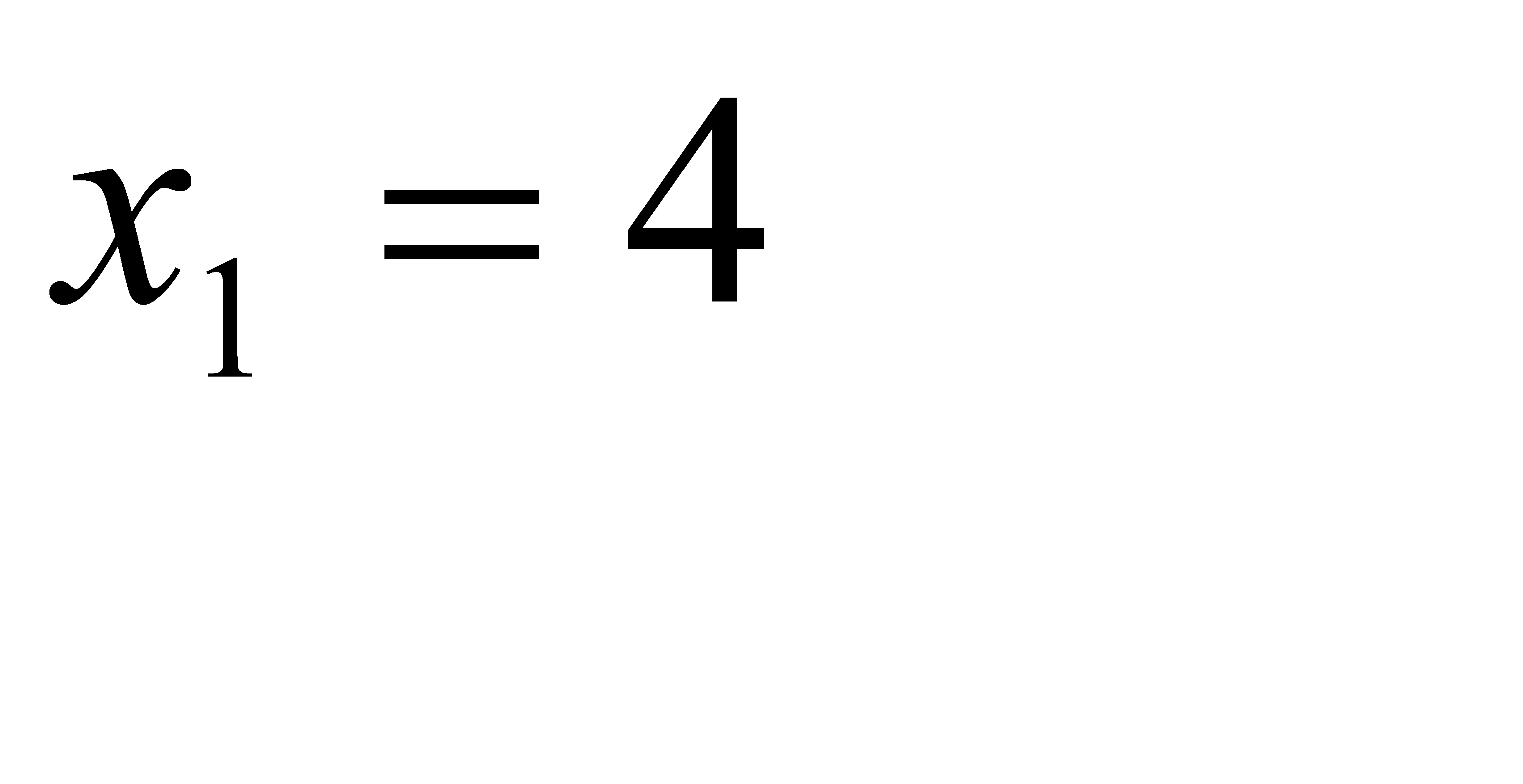 с вероятностью
с вероятностью 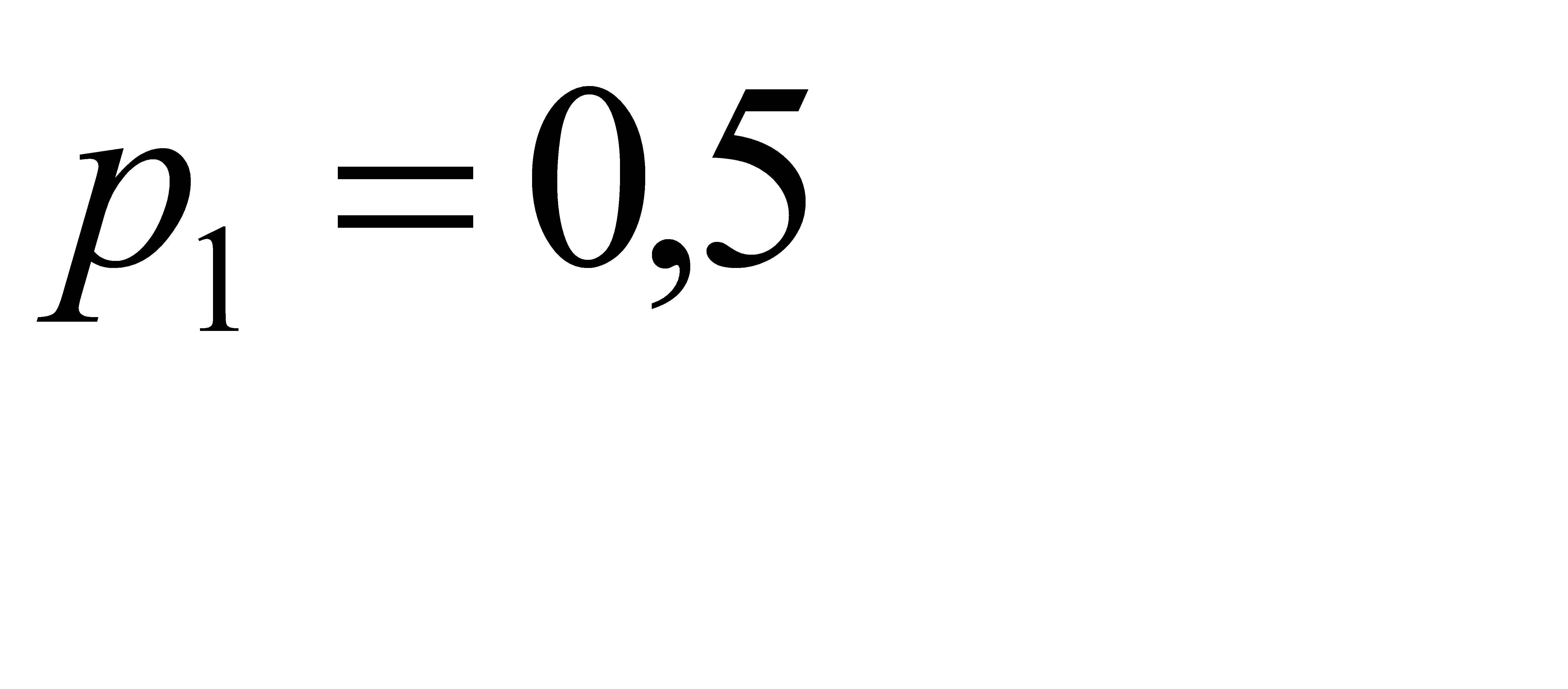 ;
; 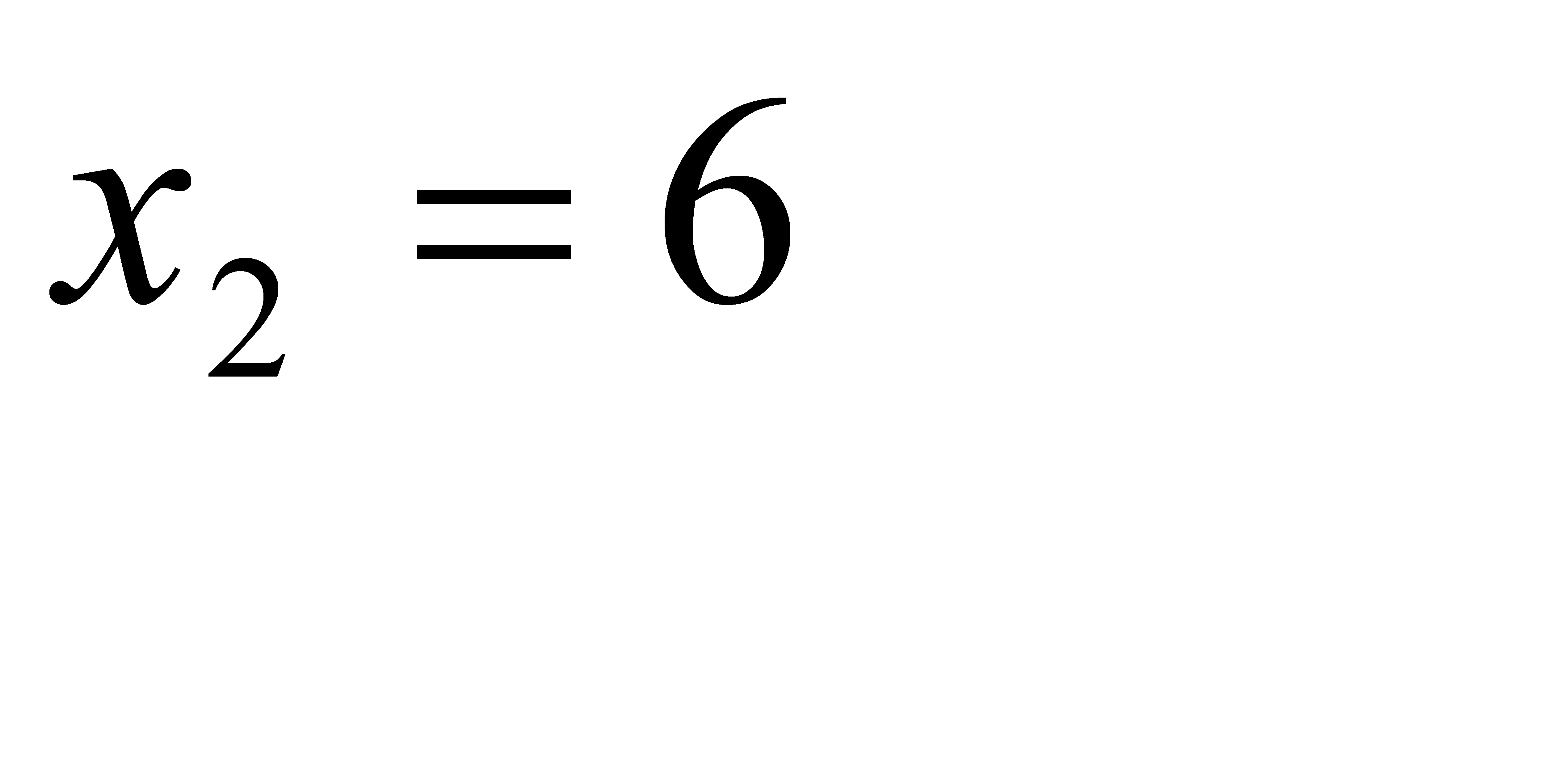 с вероятностью
с вероятностью 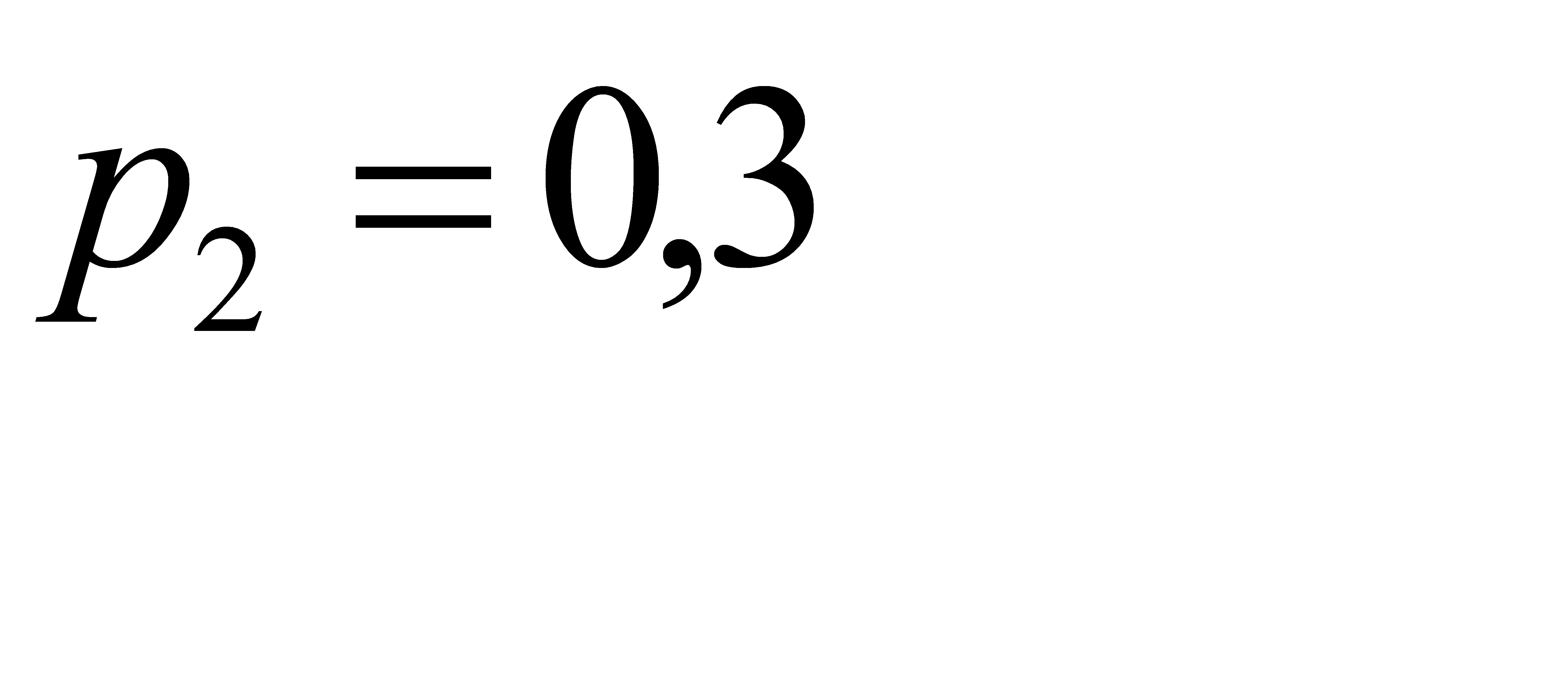 и
и 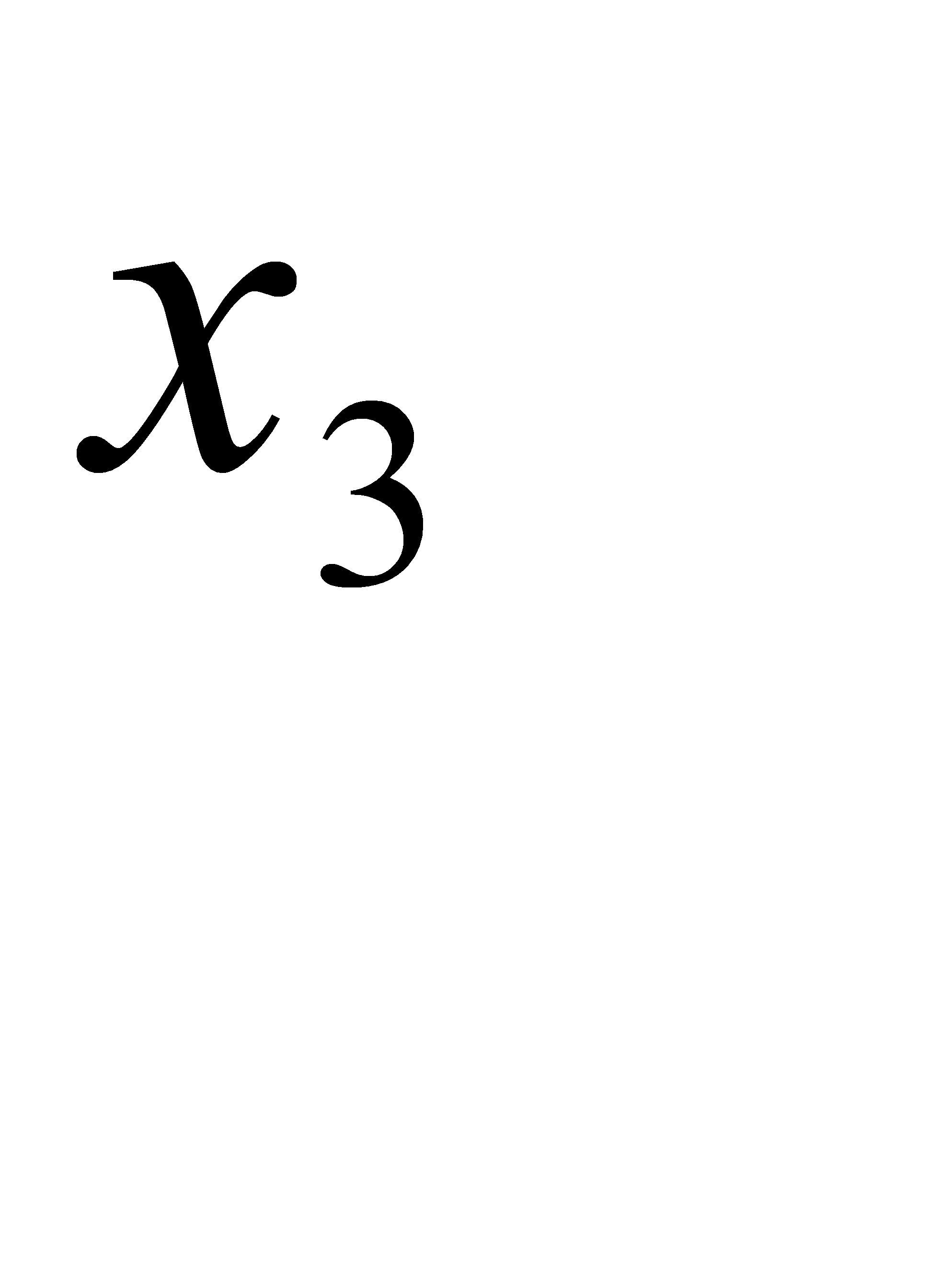 с вероятностью
с вероятностью 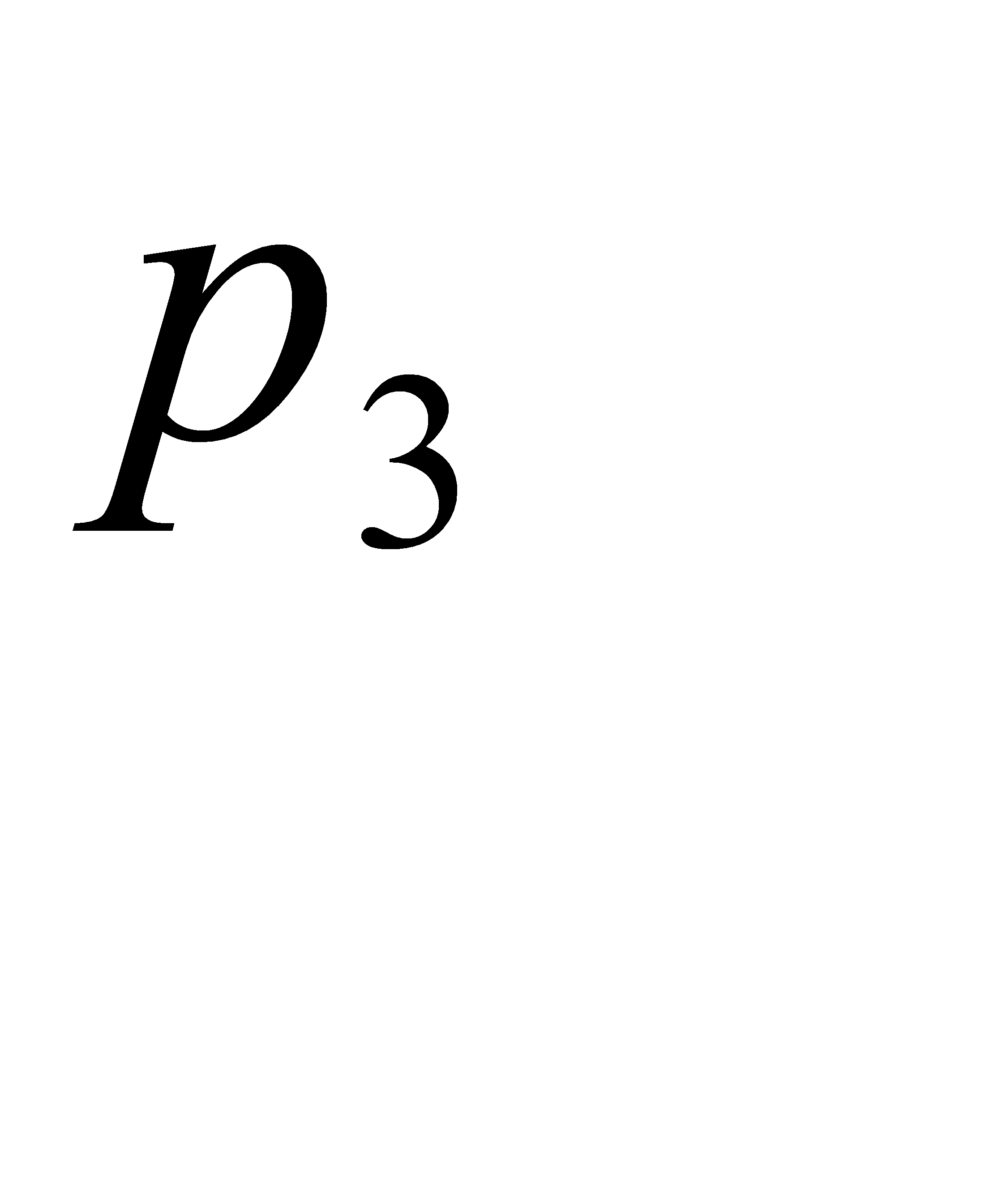 . Найти
. Найти 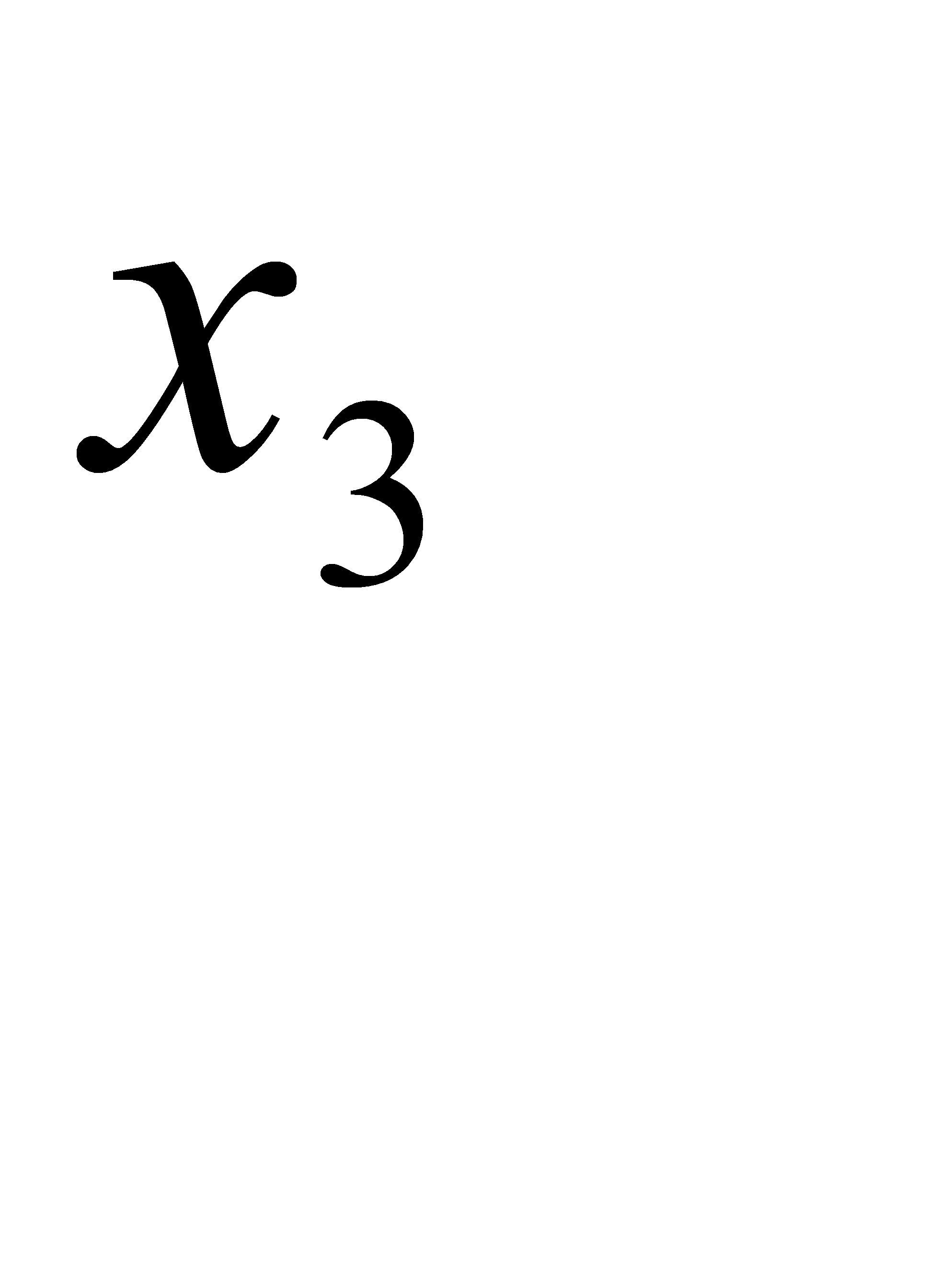 и
и 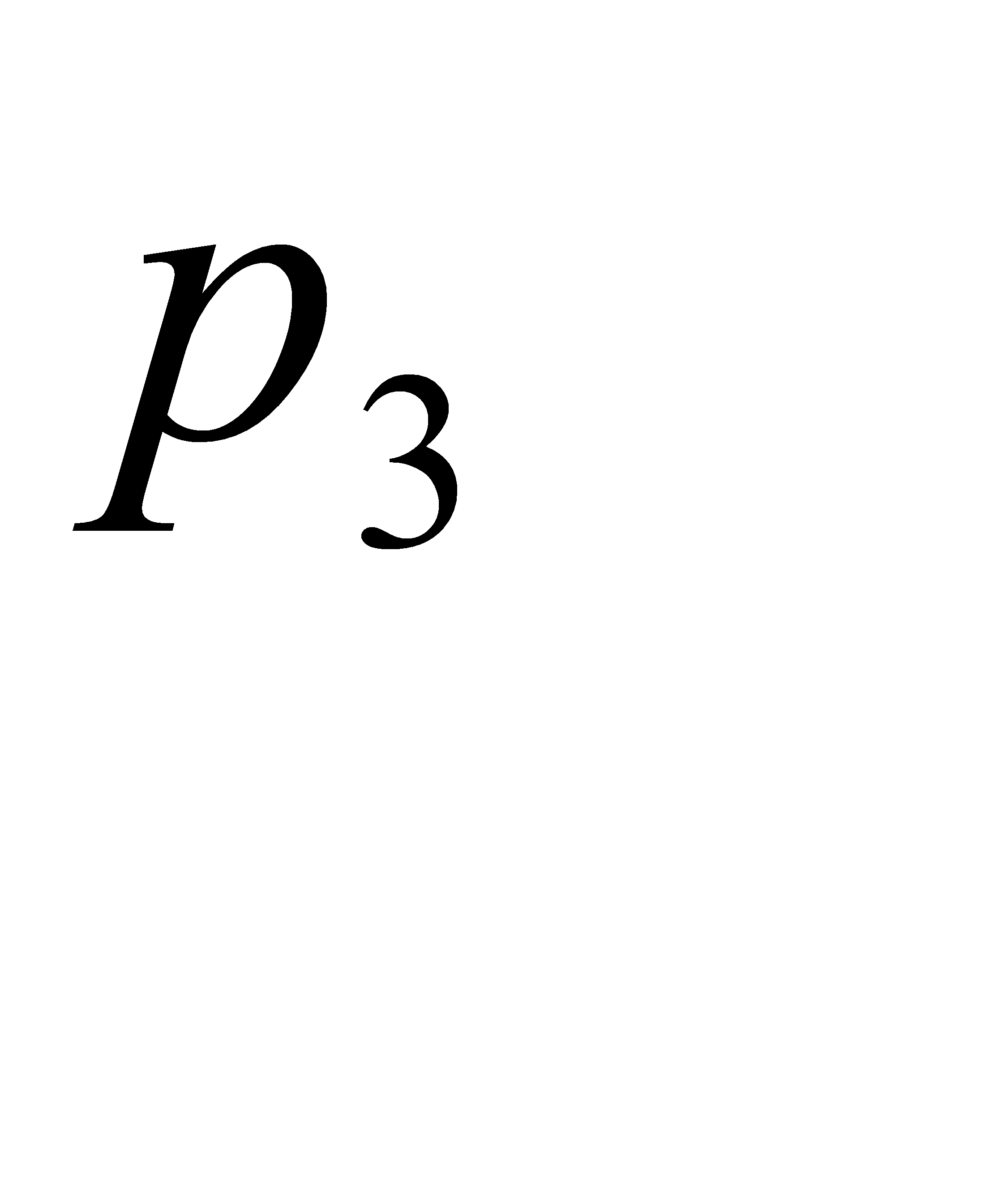 , зная, что
, зная, что 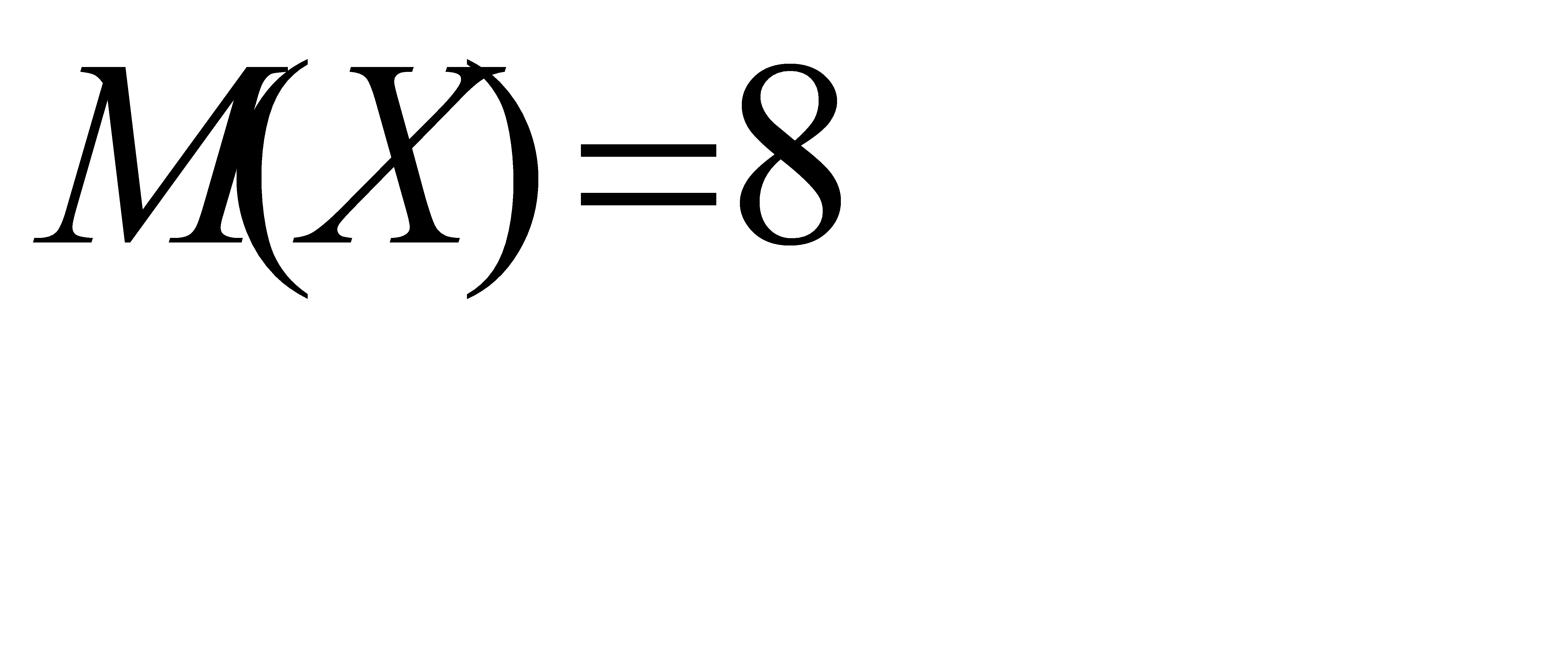 .
.
Решение.
Поскольку случайная величина принимает одно из трёх возможных значений, они образуют полную группу. Тогда 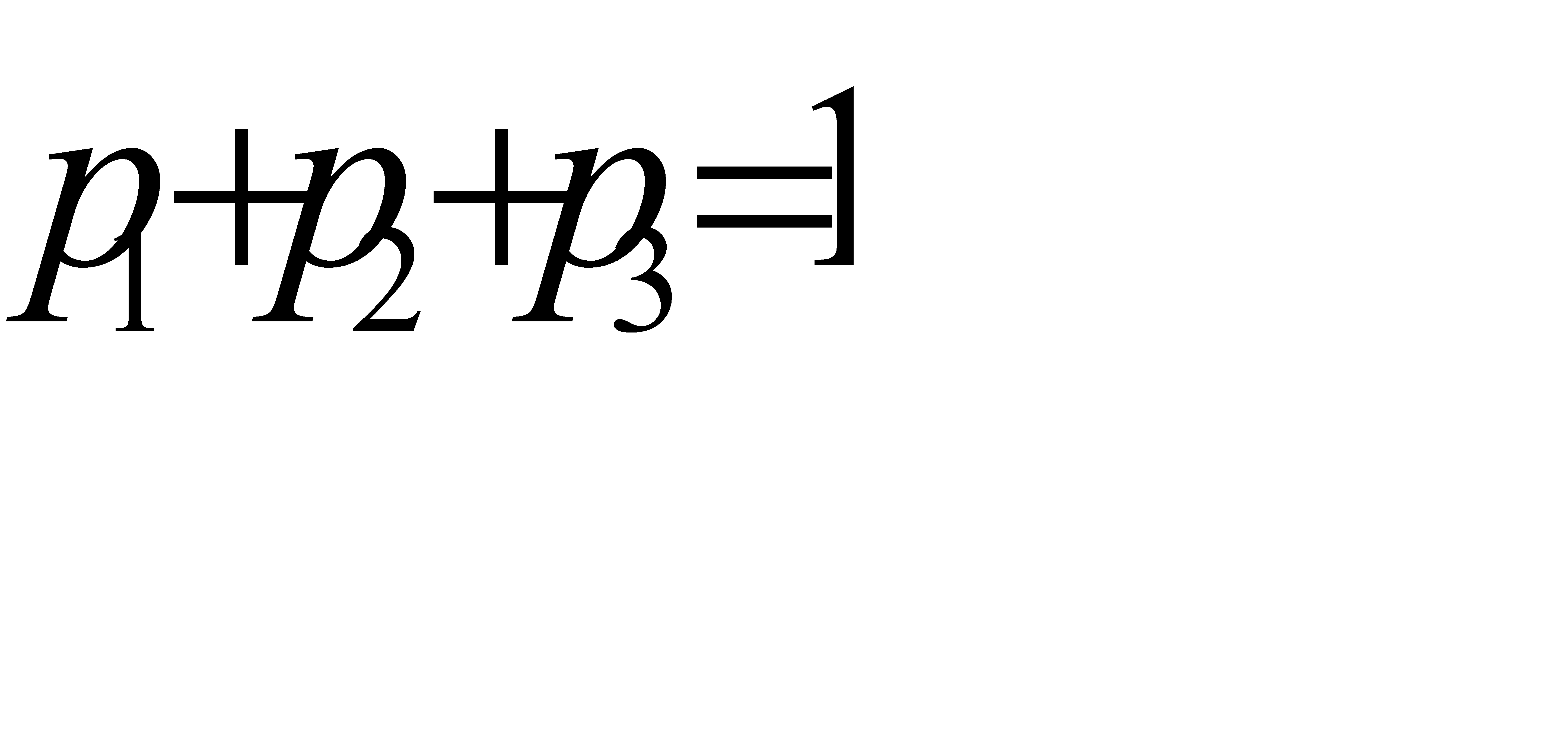 ,
, 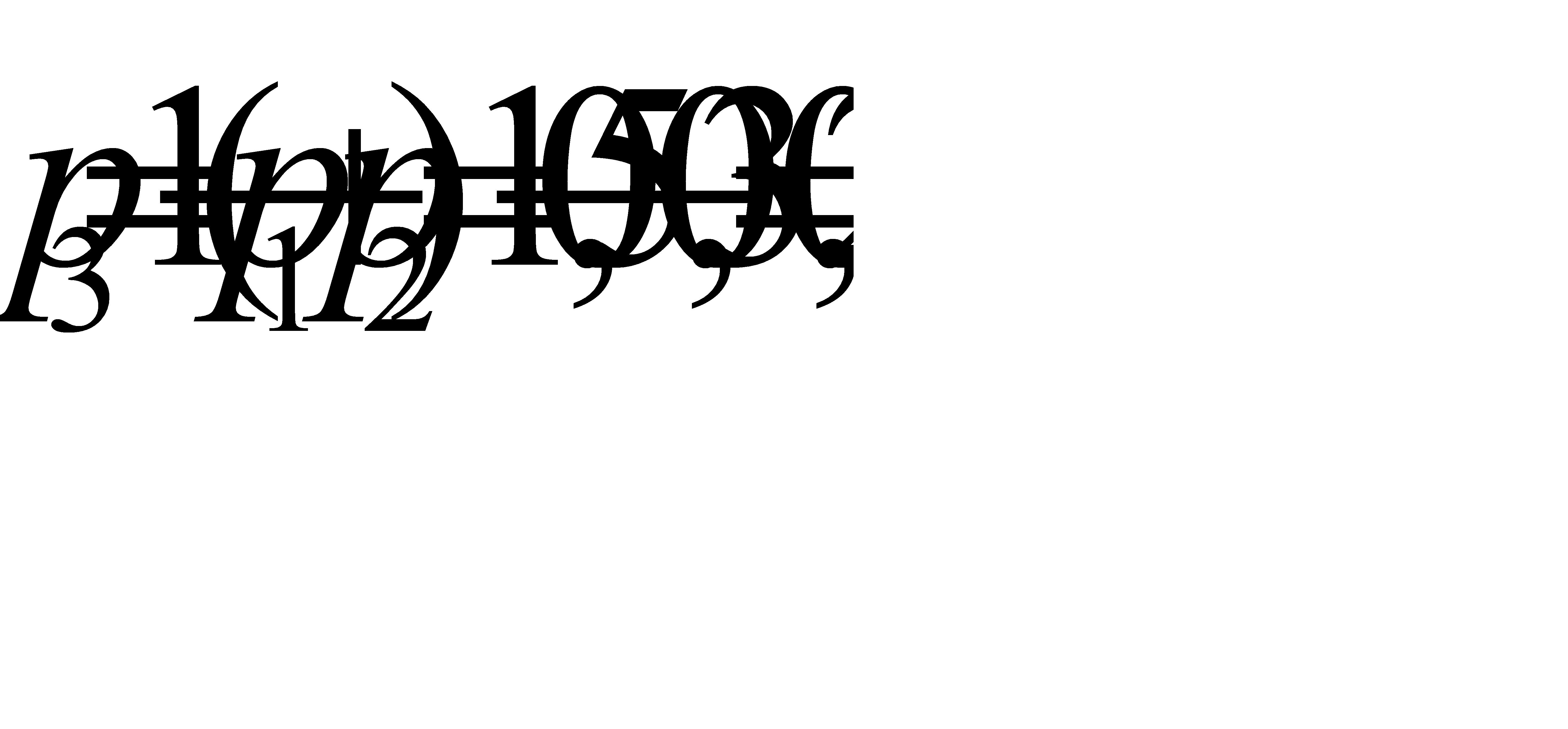 .
.
Далее, из определения математического ожидания  . Отсюда
. Отсюда 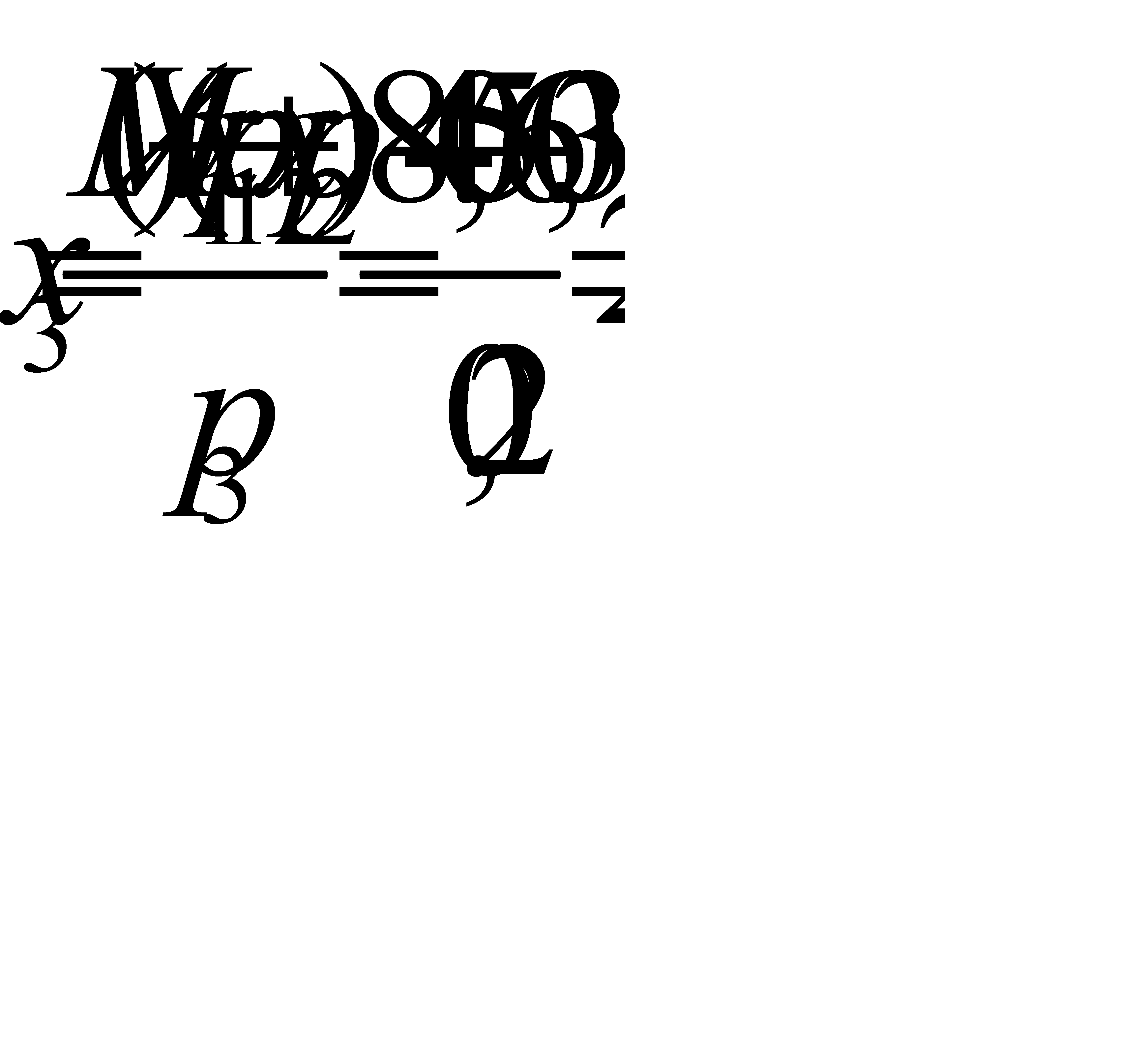 .
.
Ответ: 21.
#192
Дан перечень возможных значений дискретной случайной величины X: 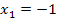 ,
, 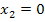 ,
, 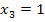 , а также известны математические ожидания этой величины и ее квадрата:
, а также известны математические ожидания этой величины и ее квадрата: 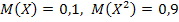 . Найти вероятности
. Найти вероятности 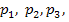 соответствующие возможным значениям
соответствующие возможным значениям 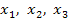 .
.
РЕШЕНИЕ.
Так как сумма вероятностей всех возможных значений X равна 1, а 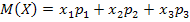 и
и 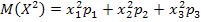 , то составим систему уравнений.
, то составим систему уравнений.
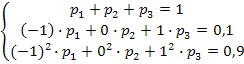
Решив ее, получим искомые вероятности: 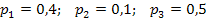 .
.
#193
Условие:
Дан перечень возможных значений дискретной случайной величины 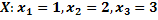 , а так же известны математические ожидания этой величины и ее квадрата:
, а так же известны математические ожидания этой величины и ее квадрата:
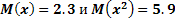 .
.
Найти вероятности, соответствующие возможным значениям 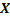 .
.
Решение:
Пользуясь тем, что сумма вероятностей всех возможных значений 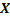 равна единице, а так же принимая во внимание, что
равна единице, а так же принимая во внимание, что 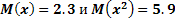 , составим следующую систему трех линейных уравнений относительно неизвестных вероятностей:
, составим следующую систему трех линейных уравнений относительно неизвестных вероятностей:
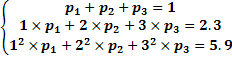
Решив эту систему, найдем искомые вероятности: 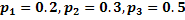
#194
В партии из 10 деталей содержится три нестандартных. Наудачу отобраны две детали. Найти математическое ожидание дискретной случайной величины X – числа нестандартных деталей среди двух отобранных.
Решение.
Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь две детали из десяти деталей, т. е. 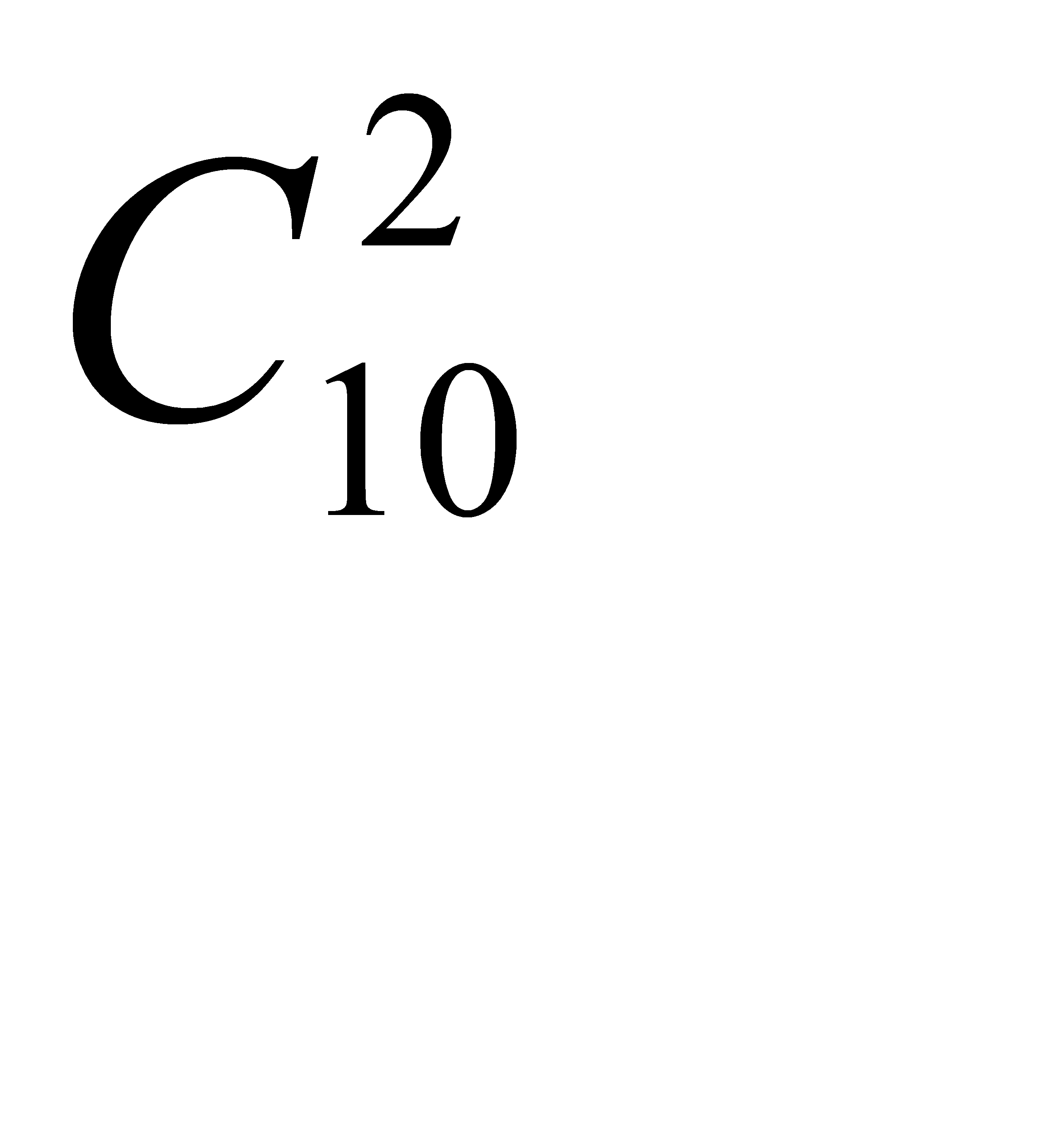 - числу сочетаний из десяти по два.
- числу сочетаний из десяти по два.
А) одну нестандартную деталь можно взять из трех нестандартных деталей 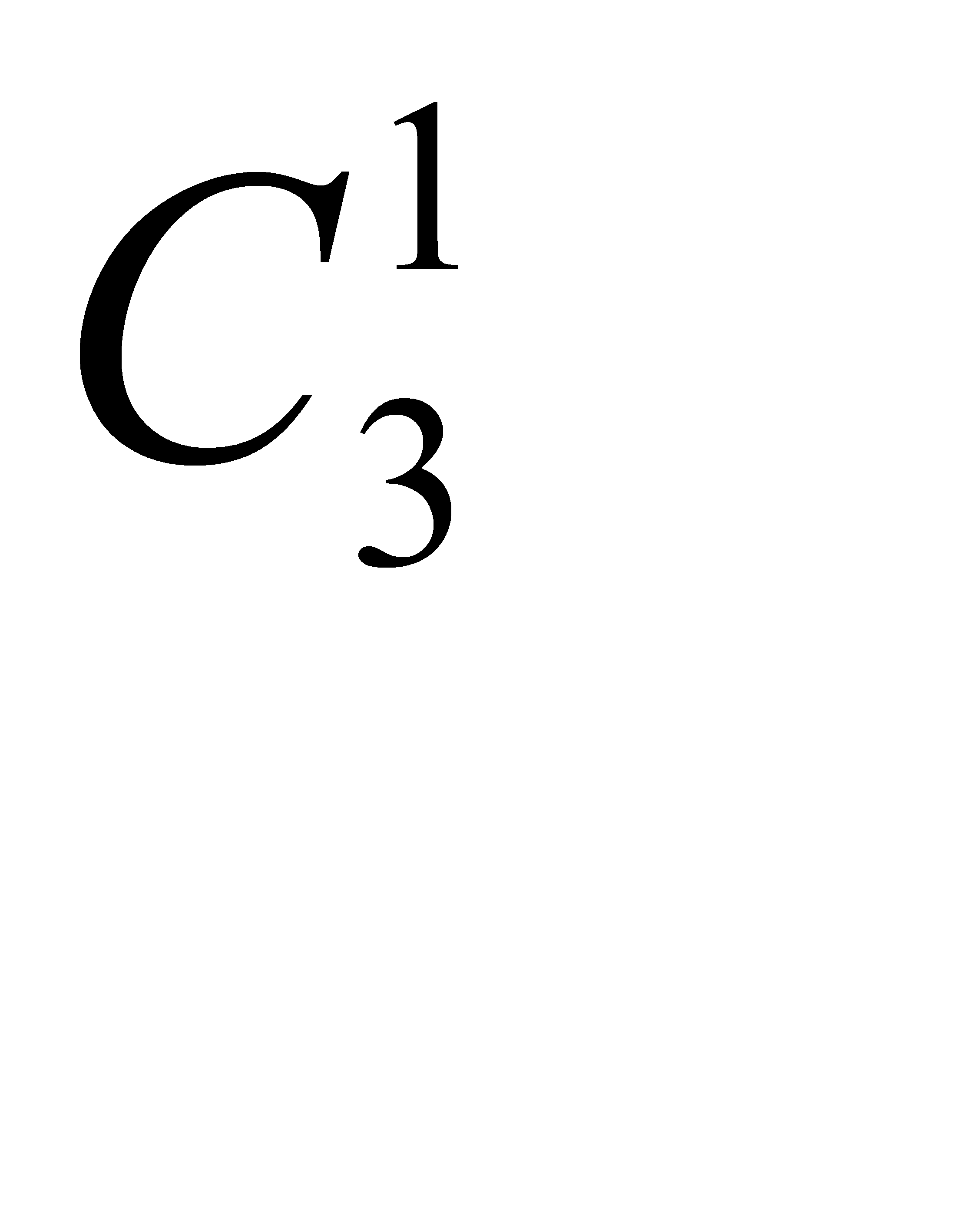 способами; при этом одна деталь должна быть нестандартной; взять же одну нестандартную деталь из семи нестандартных можно
способами; при этом одна деталь должна быть нестандартной; взять же одну нестандартную деталь из семи нестандартных можно 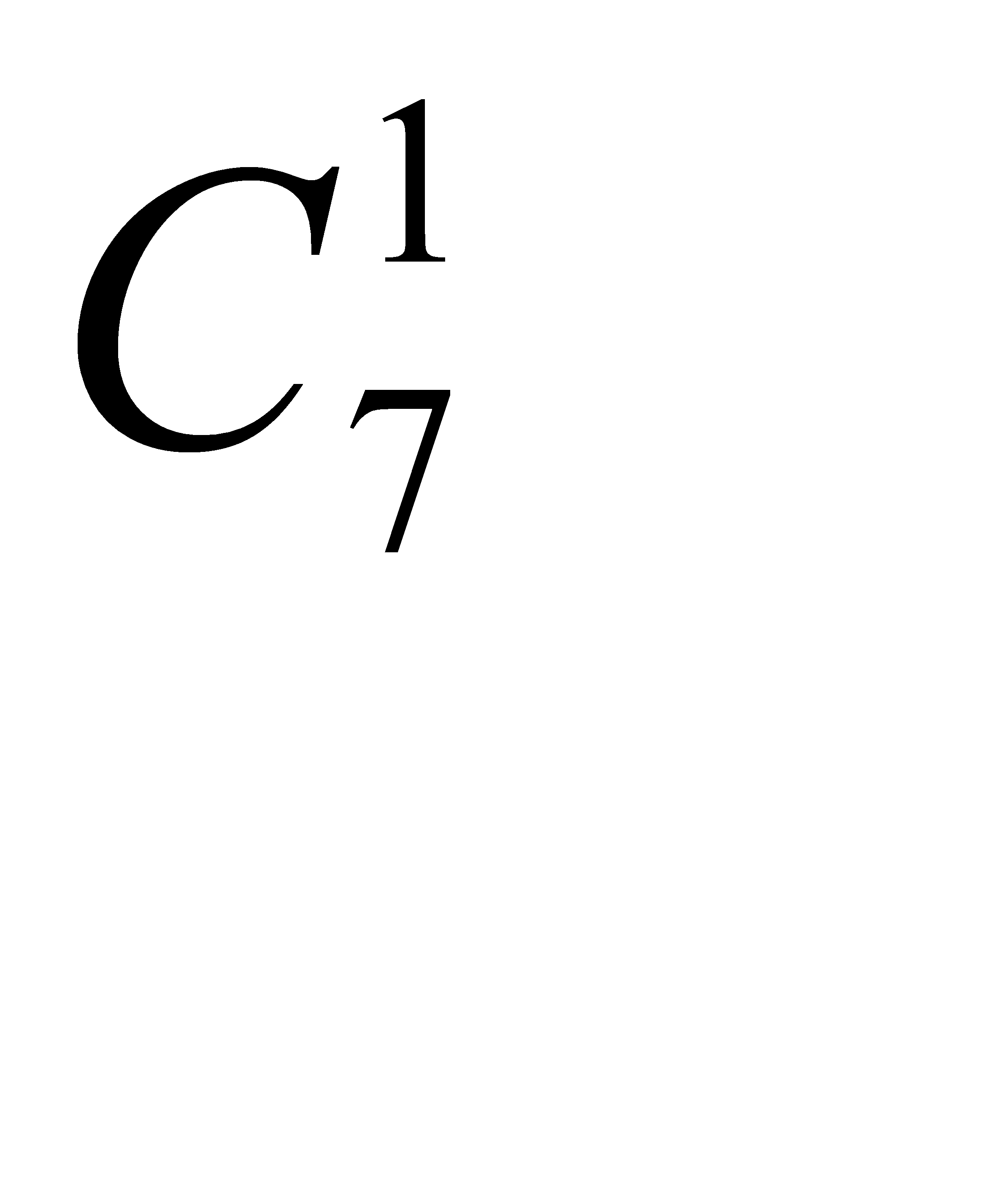 способами. Следовательно, число благоприятствующих исходов равно
способами. Следовательно, число благоприятствующих исходов равно 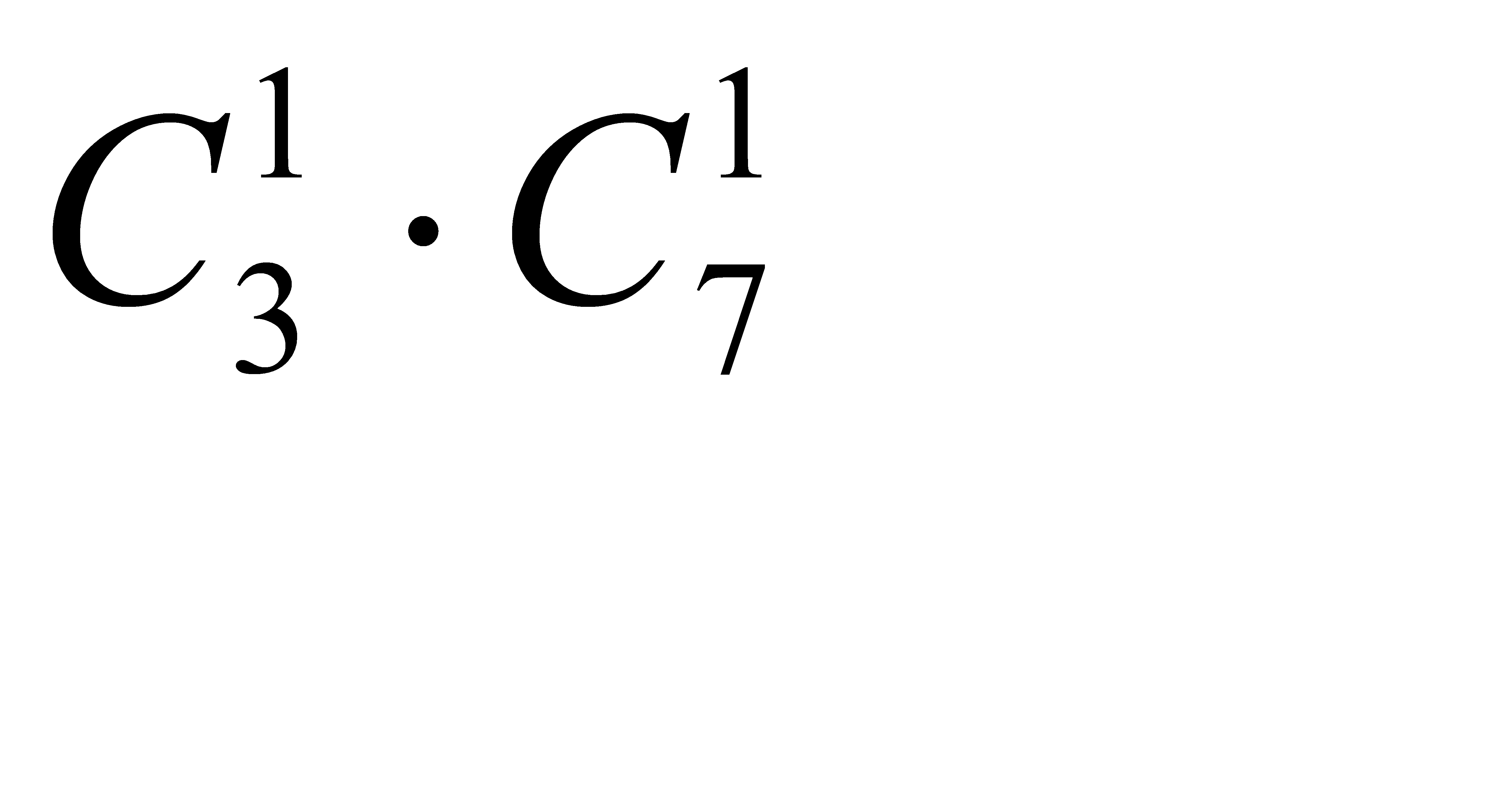
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
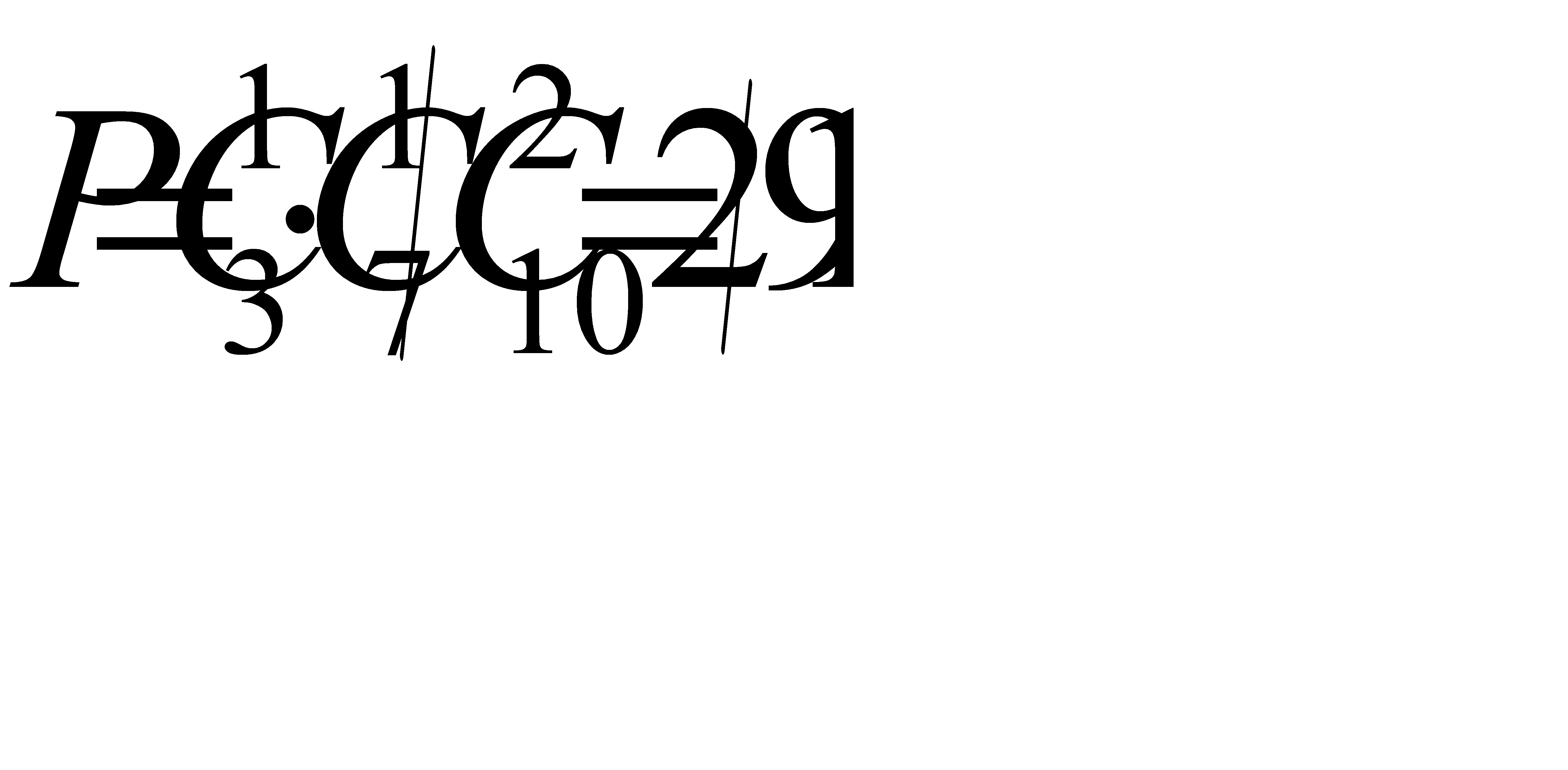
Две нестандартных детали можно взять из трех нестандартных деталей 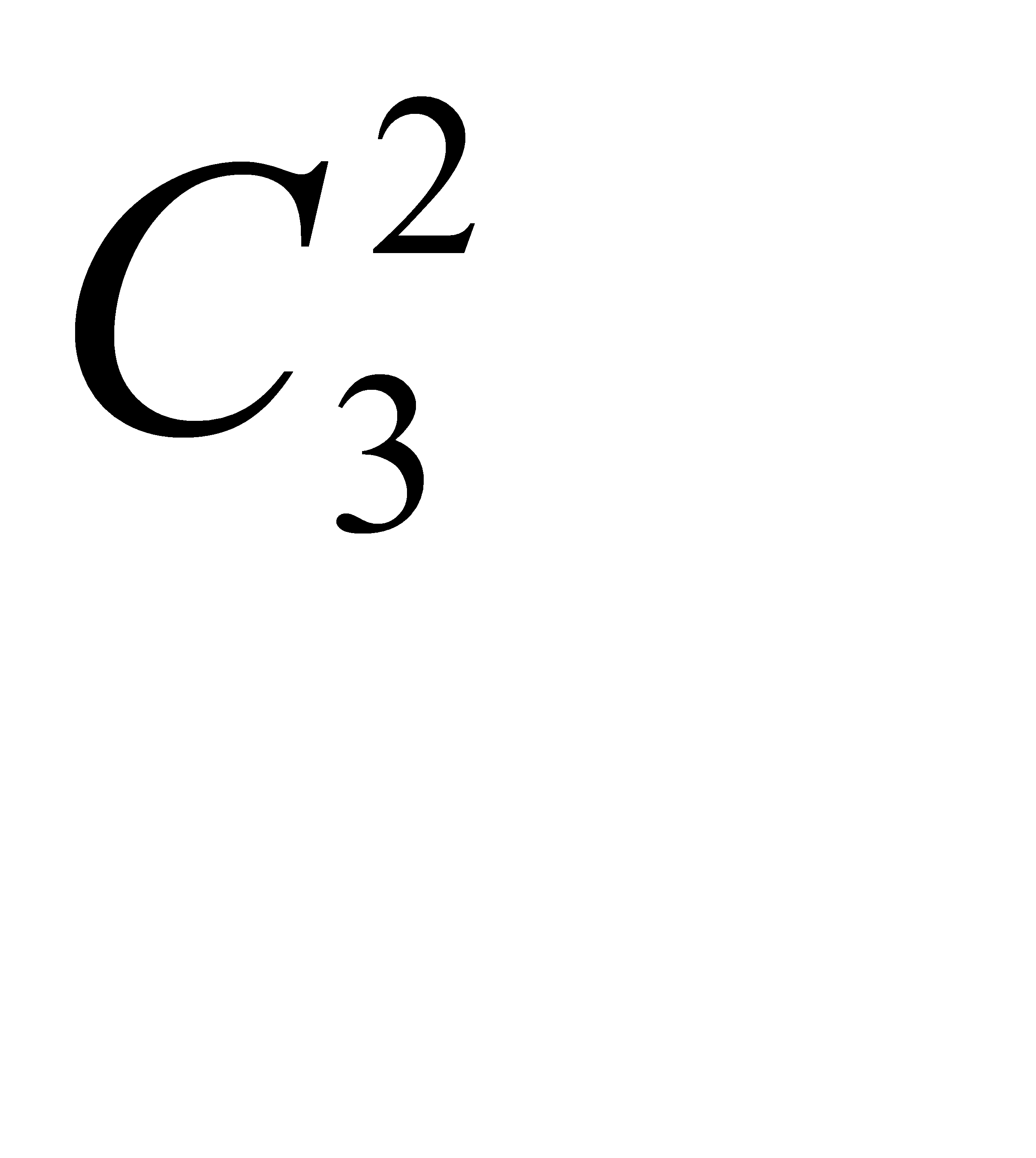 способами; Следовательно, число благоприятствующих исходов равно
способами; Следовательно, число благоприятствующих исходов равно 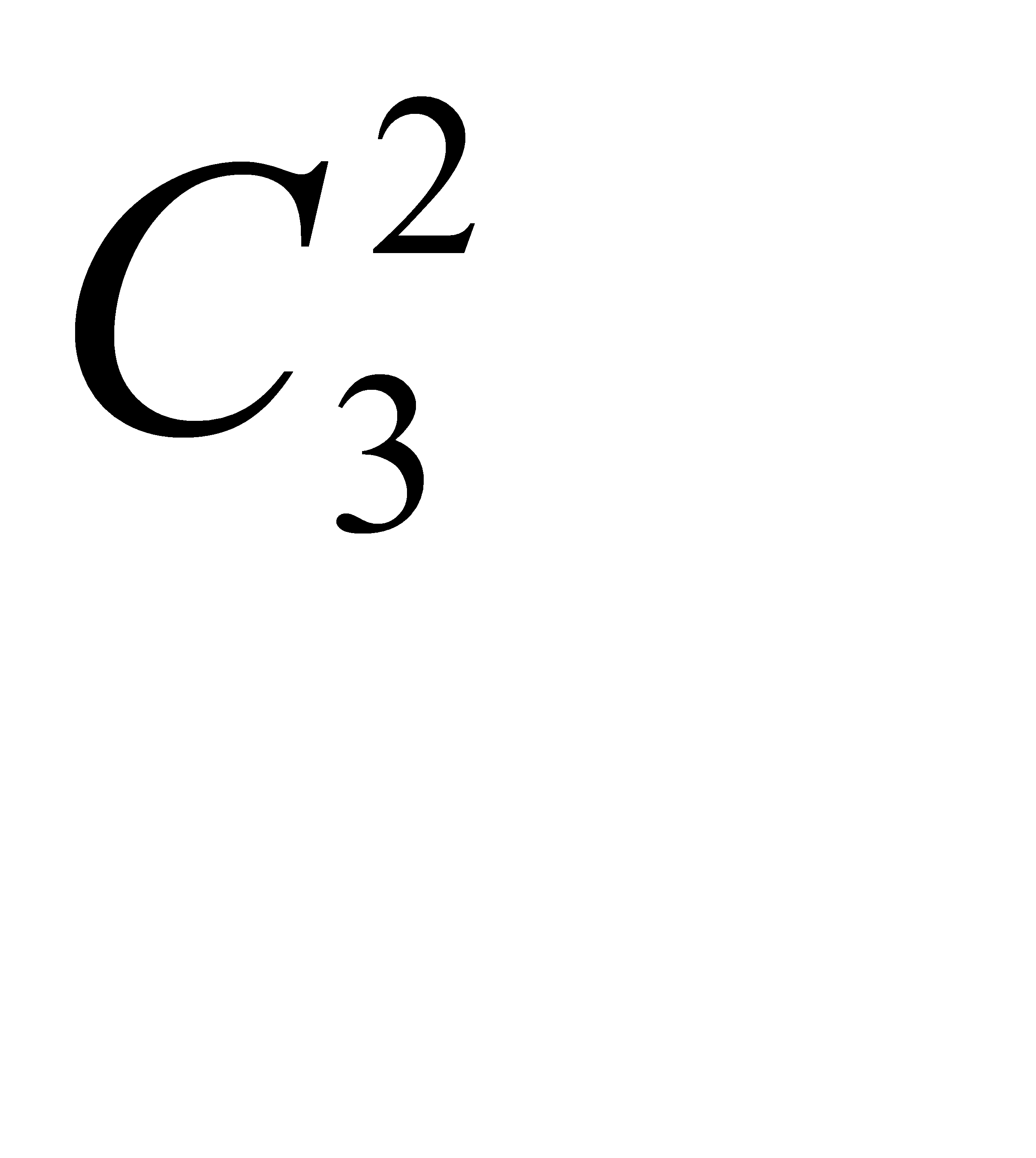
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

Математическое ожидание равно сумме произведений всех возможных значений X на их вероятности:

#195
а) Доказать, что математическое ожидание числа появлений события А в одном испытании равно вероятности р появления события А.
Указание. Дискретная случайная величина X—число появлений события в одном испытании—имеет только два возможных значения: x = l (событие А наступило)
и y = 0 (событие А не наступило).
б) Доказать, что математическое ожидание дискретной случайной величины X—числа появлений события А в n независимых испытаниях, в каждом из которых вероятность появления события равна р—равно произведению числа испытаний на вероятность появления события в одном испытании, т. е. доказать, что математическое ожидание биномиального распределения М(Х)=nр.
Решение:
а) дискретная случайная величина х задана законом распределения:
х 1 2
р р р
По формуле математического ожидания 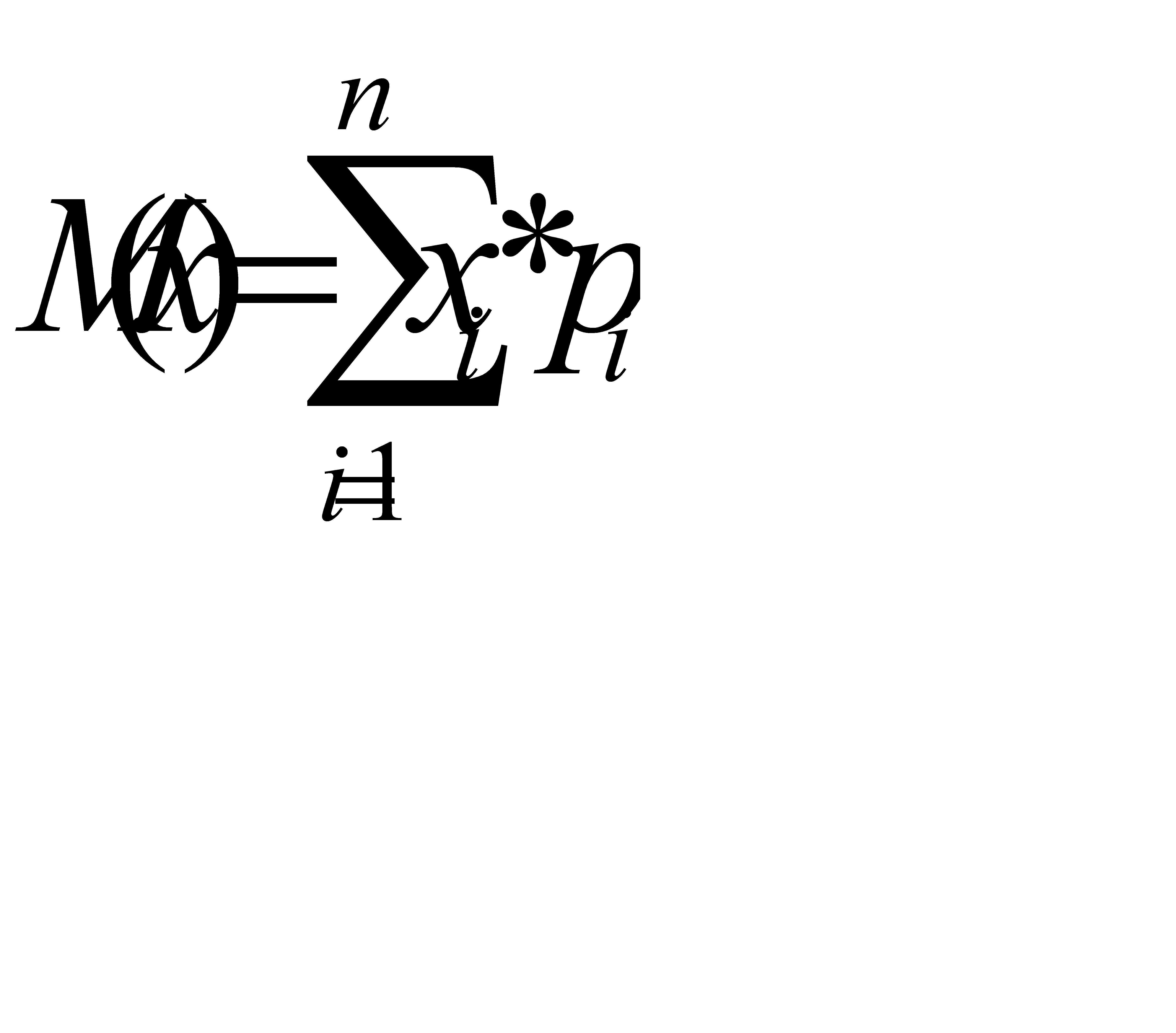 получим:
получим:
М(х)=1*р+0*р=р
Что и требовалось доказать.
б) Так как число испытаний велико, а вероятность р появления со-
бытия в каждом испытании очень мала, то воспользуемся законом Пуассона.
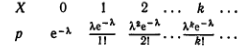
По определению математического ожидания для
случая, когда число возможных значений X есть счетное множество, 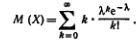
Учитывая, что при к=0 первый член суммы равен нулю, при-
примем в качестве наименьшего значения k единицу:
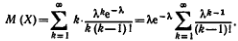
Положив k—l=m, получим
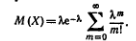
Принимая во внимание, что
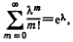 получим:
получим:
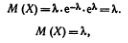
А так как λ =np то получим M(x)=np что и требовалось доказать.
#196
Найти математическое ожидание дискретной случайной величины Х – числа таких бросаний пяти игральных костей, в каждом из которых на двух костях появится по одному очку, если общее число бросаний равно двадцати.
Решение
Воспользуемся формулой
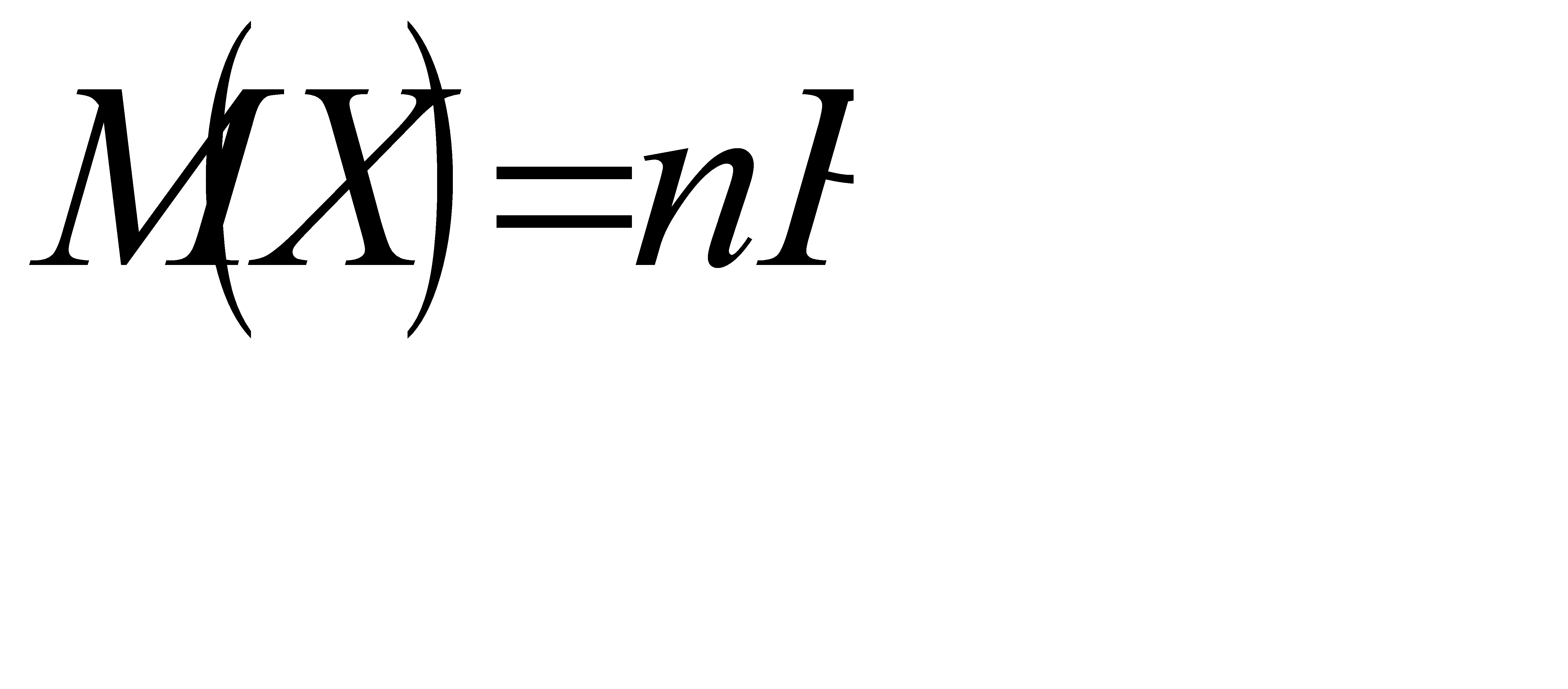 ,
,
Где n – общее число испытаний (бросаний пяти костей); Х – число появлений интересующего нас события (на двух костях из пяти появится по одному очку) в n испытаниях; Р – вероятность появления рассматриваемого события в одном испытании.
По условию, n = 20. Остаётся найти Р – вероятность того, что на гранях двух из пяти костей появится по одному очку. Эту вероятность вычислим по формуле Бернулли, учитывая, что вероятность появления одного очка на грани одной кости p = 1/6, следовательно q = 5/6:
 .
.
Искомое математическое ожидание

Ответ: 3
#197
Задание: Устройство состоит из 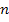 элементов. Вероятность отказа любого элемента за время опыта равна
элементов. Вероятность отказа любого элемента за время опыта равна 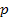 . Найти математическое ожидание числа таких опытов, в каждом из которых откажет ровно
. Найти математическое ожидание числа таких опытов, в каждом из которых откажет ровно 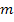 элементов, если всего произведено
элементов, если всего произведено 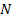 опытов. Предполагается, что опыты независимы один от другого.
опытов. Предполагается, что опыты независимы один от другого.
Решение: Обозначим через 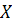 число опытов, в которых откажет ровно
число опытов, в которых откажет ровно 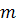 элементов. Так как опыты независимы и вероятности интересующего нас события (в одном опыте откажет ровно
элементов. Так как опыты независимы и вероятности интересующего нас события (в одном опыте откажет ровно 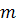 элементов) в этих опытах одинаковы, то применима формула
элементов) в этих опытах одинаковы, то применима формула

где 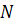 —общее число опытов;
—общее число опытов; 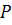 —вероятность того, что в одном опыте откажет ровно
—вероятность того, что в одном опыте откажет ровно 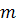 элементов. Найдем вероятность
элементов. Найдем вероятность 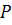 по формуле Бернулли:
по формуле Бернулли:

Подставив (**) в (*), получим искомое математическое ожидание:
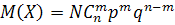
198.....
#199
Обозначим через 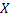 сумму числа очков, которые выпадут на всех гранях, через
сумму числа очков, которые выпадут на всех гранях, через 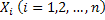 – число выпавших очков на грани
– число выпавших очков на грани 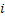 -й кости. Тогда, очевидно,
-й кости. Тогда, очевидно,
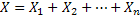
Следовательно,
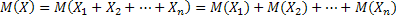
Очевидно, все величины 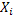 имеют одинаковое распределение, а следовательно одинаковые числовые характеристики и, в частности, одинаковые математические ожидания, т. е.
имеют одинаковое распределение, а следовательно одинаковые числовые характеристики и, в частности, одинаковые математические ожидания, т. е. 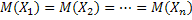 .
.
В силу (*) получим
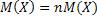 (**)
(**)
Таким образом, достаточно вычислить математическое ожидание величины 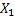 , т. е. математическое ожидание числа очков, которые могут выпасть на первой кости. Для этого напишем закон распределения
, т. е. математическое ожидание числа очков, которые могут выпасть на первой кости. Для этого напишем закон распределения 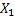 :
:
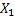
| ||||||
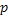
| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Найдем 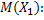
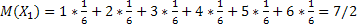 (***)
(***)
Подставив (***) в (**), окончательно получим
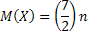
#200
Математическое ожидание дискретной случайной величины X равно произведению числа испытаний на вероятность появления события.
В данном случае можно использовать формулу Бернулли
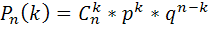
В данной задаче, по условию, k=4, n=5, p=0, 9, q=0, 1
Находим вероятность
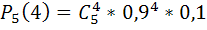
Так как проверяется 50 партий, то найденную вероятность нужно умножить на 50
Получаем М(Х)=50* 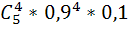 =16, 4025≈ 16
=16, 4025≈ 16
201. Доказать: 1) М(Y)=аМ(Х)+b, если Y=аХ+b; 2) М(Y)= i=1n∑ аiМ(Хi)+b, если Y= i=1n∑ (аiХi)+b.
Решение:
1) М(Y)=М(аХ+b)=(ах1+b)р1+ (ах2+b)р2+…+ (ахn+b)рn=ах1р1+ ах2р2+…+ ахnрn+bр1+ bр2+…+ bрn=
=а(х1р1+ х2р2+…+ хnрn)+b(р1+ р2+…+ рn)= а(х1р1+ х2р2+…+ хnрn)+b=аМ(Х)+b.
Что и требовалось доказать.
2) М(Y)=М(i=1n∑ (аiХi)+b)= i=1n∑ (аiХi 1)*р1+ i=1n∑ (аiХi 2)*р2+…+ i=1n∑ (аiХin)*рn+М(b)=
= i=1n∑ аi*( i=1n∑ Хi 1*р1+ i=1n∑ Хi 2*р2+…+ i=1n∑ Хi n*рn)+b= i=1n∑ ai* i=1n∑ M(Xi)+b= i=1n∑ аiМ(Хi)+b
Что и требовалось доказать.
#202
События A1, A2, …, An несовместны и образуют полную группу; вероятности появления этих событий соответственно равны p1, p2, …, pn. Если в итоге испытания появляется событие Aii=1, …, n, то дискретная случайная величина X принимает возможное значение xi, равное вероятности pi появления события Ai. Доказать, что математическое ожидание случайной величины Х имеет наименьшее значение, если вероятности всех событий одинаковы.
Решение: Возможные значения величины Х по условию равны вероятности pi событий Ai; вероятность возможного значения pi, очевидно, также равна pi. Таким образом, X имеет следующее распределение:
| X | p1 | p2 | … | pn |
| P | p1 | p2 | … | pn |
Найдем математическое ожидание:
MX=p12+p22+…+pn2. (*)
Рассматриваемые события образуют полную группу, поэтому:
p1+p2+…+pn=1.
Из дифференциального исчисления известно, что если сумма независимых переменных постоянна, то сумма квадратов этих переменных имеет наименьшее значение в случае равенства переменных. Применительно к рассматриваемой задаче это означает: сумма (*), т. е. математическое ожидание М (X), имеет наименьшее значение, если вероятности всех событий, образующих полную группу, равны между собой, что и требовалось доказать.
#203
Доказать, что математическое ожидание дискретной случайной величины заключено между наименьшим и наибольшим ее возможными знаениями.
Решение: Пуст Х – дискретная случайная величина, заданная законом распределения:
| X | x1 | x2 | x3 | … | xn |
| p | p1 | p2 | p3 | … | pn |
Обозначим наименьшее и наибольшее значения X соответственно через m и M. Тогда 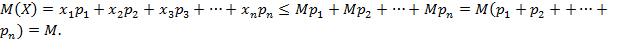
Итак, 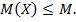
Аналогично можно вывести, что 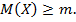
Объединяя, получим 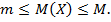 Ч. Т. Д.
Ч. Т. Д.
#204
Дискретная случайная величина X принимает k положительных значений 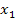 ,
, 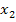 , …,
, …, 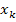 с вероятностями, равными соответственно
с вероятностями, равными соответственно 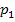 ,
, 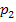 , …,
, …, 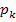 . Предполагая, что возможные значения записаны в возрастающем порядке, доказать, что
. Предполагая, что возможные значения записаны в возрастающем порядке, доказать, что
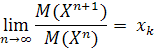
Решение: Принимая во внимание, что 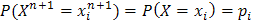 и
и 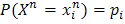 , получим
, получим
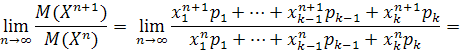
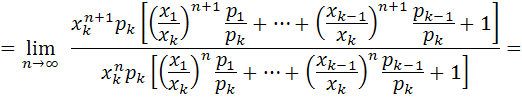
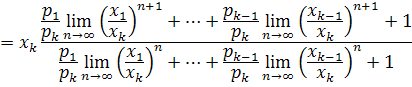
Так как по условию возможные значения X записаны в возрастающем порядке, т. е. 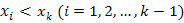 , то
, то
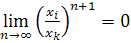 и
и 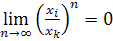 .
.
Следовательно,
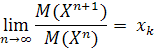
Предположение доказано.
#205
Доказать, что если случайные величины Х1, Х2, …Хn независимы, положительны и одинаково распределены, то
MX1X1+X2+…+Xn=1n
Решение.
Введем в расмотрение случайные величины
Y1=X1X1+X2+…+Xn, Y2=X2X1+X2+…+Xn, …, Yn=XnX1+X2+…+Xn. *
Заметим, что знаменатели этих дробей не могут быть равными нулю, поскольку величины Yi также одинаково распределены и, следовательно, имеют одинаковые числовые характеристики, в частности, одинаковые математические ожидания:
MY1=MY2=…=MYn. **
Легко видеть, что Y1+Y2+…+Yn=1, следовательно,
M(Y1+Y2+…+Yn)=M1=1.
Математическое ожидание суммы равно сумме математических ожиданий слагаемых, поэтому
MY1+MY2+…+MYn=1.
В силу (**) имеем nM(Y1)=1. Отсюда M(Y1)=1/n.
Учитывая (*), окончательно получим
MX1X1+X2+…+Xn=1n.
Что и требовалось доказать.
#206
Доказать, что если случайные величины Х1, Х2, Х3, Х4, Х5 независимы, положительны и одинаково распределены, то
MX1+X2+X3X1+X2+X3+X4+X5=35.
Указание. Представить дробь, стоящую под знаком математического ожидания, в виде суммы трех дробей и воспользоваться решением задачи 205.
Решение.
Введем в расмотрение случайные величины
Y1=X1X1+X2+X3+X4+X5, Y2=X2X1+X2+X3+X4+X5, Y3=X3X1+X2+X3+X4+X5. *
Заметим, что знаменатели этих дробей не могут быть равными нулю, поскольку величины Yi также одинаково распределены и, следовательно, имеют одинаковые числовые характеристики, в частности, одинаковые математические ожидания:
MY1=MY2=MY3. **
Легко видеть, что Y1+Y2+Y3=1, следовательно,
M(Y1+Y2+Y3)=M1=1.
Математическое ожидание суммы равно сумме математических ожиданий слагаемых, поэтому
MY1+MY2+…+MYn=1.
В силу (**) имеем 5M(Y1)=1. Отсюда M(Y1)=1/5.
Учитывая (*), окончательно получим
MX1+X2+X3X1+X2+X3+X4+X5=35.
Что и требовалось доказать.
#207
Найти математическое ожидание дискретной случайной величины X, распределенной по закону Пуассона:
| X | … | k | … | |||
| P | 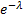
| λ 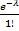
| λ 2 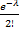
| … | λ k 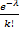
| ... |
Решение.
По определению математического ожидания для случая, когда число возможных значений X есть счетное множество,
M(X) = 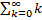 * λ k
* λ k 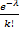 .
.
Учитывая, что при k=0 первый член суммы равен нулю, примем в качестве наименьшего значения k единицу:
M(X) = 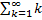 * λ k
* λ k 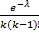 =λ
=λ 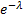
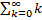 *
* 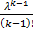
Положив k-1=m, получим
M(X)=λ 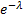
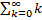 *
* 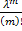
Принимая во внимание, что 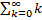 *
* 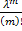 =
= 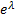 , окончательно имеем
, окончательно имеем
M(X)= λ *e-λ *eλ = λ.
Итак,
М(X)= λ,
Т. е. математическое ожидание распределения Пуассона равно параметру этого распределения λ.
#208
Случайные величины X и Y независимы. Найти
дисперсию случайной величины Z = 3X + 2Y, если из-
известно, что D(Х) = 5, D(Y) = 6.
Решение. Так как величины X и Y независимы, то незави-
независимы также и величины ЗА" и 2Y. Используя свойства дисперсии
(дисперсия суммы независимых случайных величин равна сумме
дисперсий слагаемых; постоянный множитель можно вынести за знак
дисперсии, возведя его в квадрат), получим
D (Z) = D {ZX+2Y) = D CX)+? > BY) = 9D (X) + W (К)=9• 5+4. 6=69.
#209
Случайные величины X и Y независимы. Найти дисперсию случайной величины Z=2X+3Y, если известно, что D(X)=4, D(Y)=5.
Решение. Так как величины X и Y независимы, то независимы также и величины 2X и 3Y. Используя свойства дисперсии получим:
D(Z)=D(2X+3Y)=D(2X)+D(3Y)=4D(X)+9D(Y)=4*4+9*5=61.
#210
Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины X, заданной законом распределения:
| X | -5 | |||
| p | 0, 4 | 0, 3 | 0, 1 | 0, 2 |
РЕШЕНИЕ.
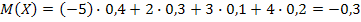
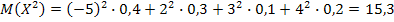
Найдем искомую дисперсию: 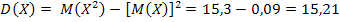 .
.
Найдем искомое отклонение: 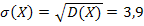 .
.
#211
Условие:
Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины 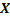 , заданной законом распределения:
, заданной законом распределения:
a) 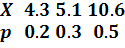 б)
б) 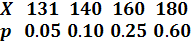
Решение:
Для вычисления дисперсии воспользуемся формулой:
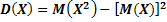
Найдем математическое ожидание 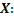
а) 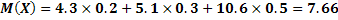
б) 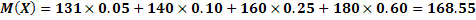
Напишем закон распределения для 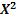 :
:
a) 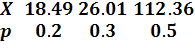 б)
б) 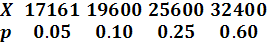
Найдем математическое ожидание 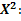
а) 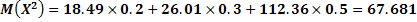
б) 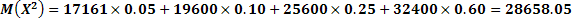
Найдем искомую дисперсию:
а) 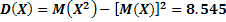
б) 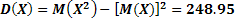
Найдем искомое среднее квадратическое отклонение:
a) 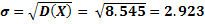
б) 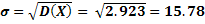
#212
Дискретная случайная величина Х имеет только два возможных значения х1 и х2, причем равновероятных. Доказать, что дисперсия величины Х равна квадрату полуразности возможных значений;
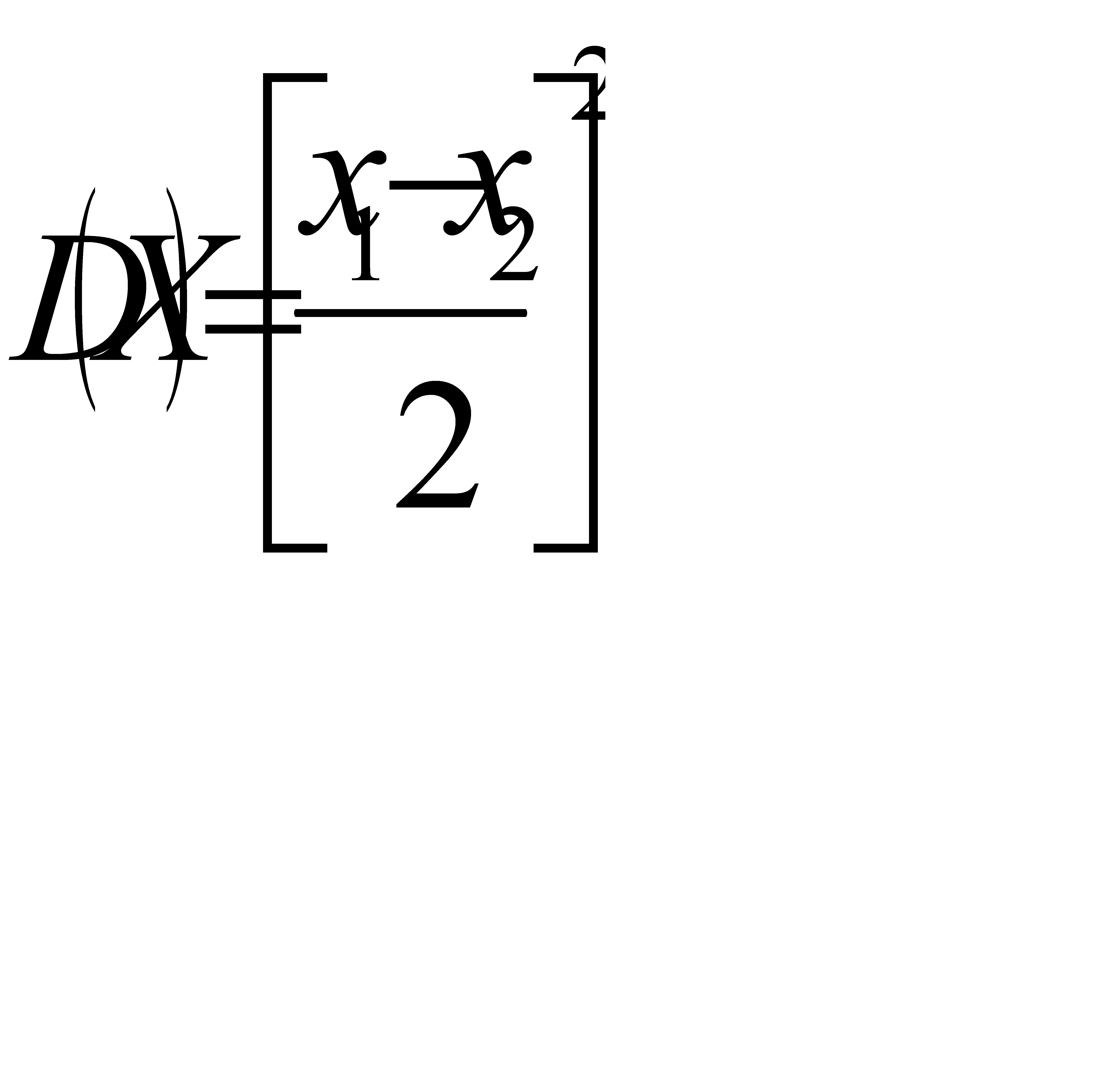 .
.
Решение: найдем математическое ожидание Х, учитывая, что вероятности возможных значений х1 и х2 и, следовательно, каждая из них равна ½;
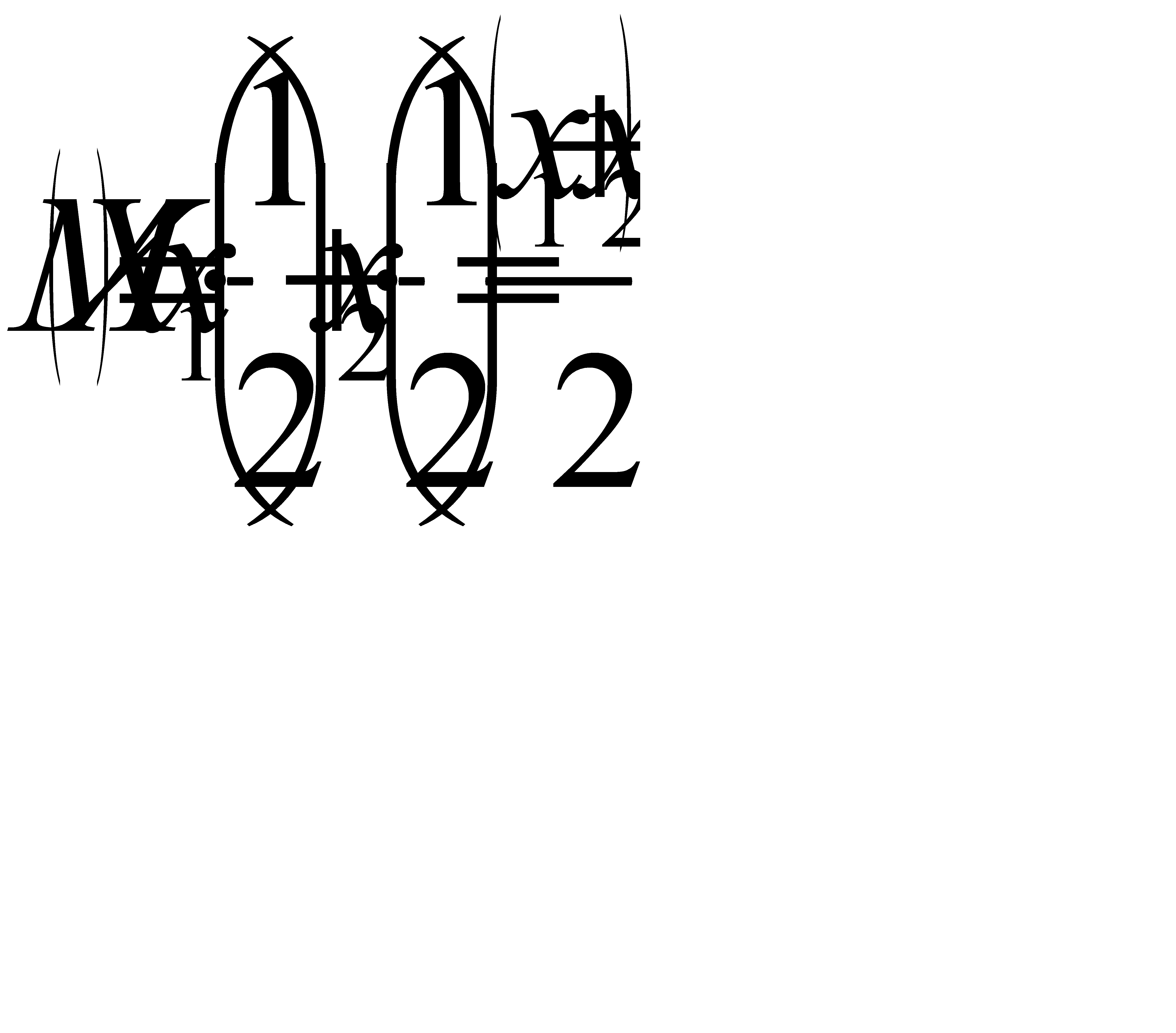 .
.
Найдем математическое ожидание 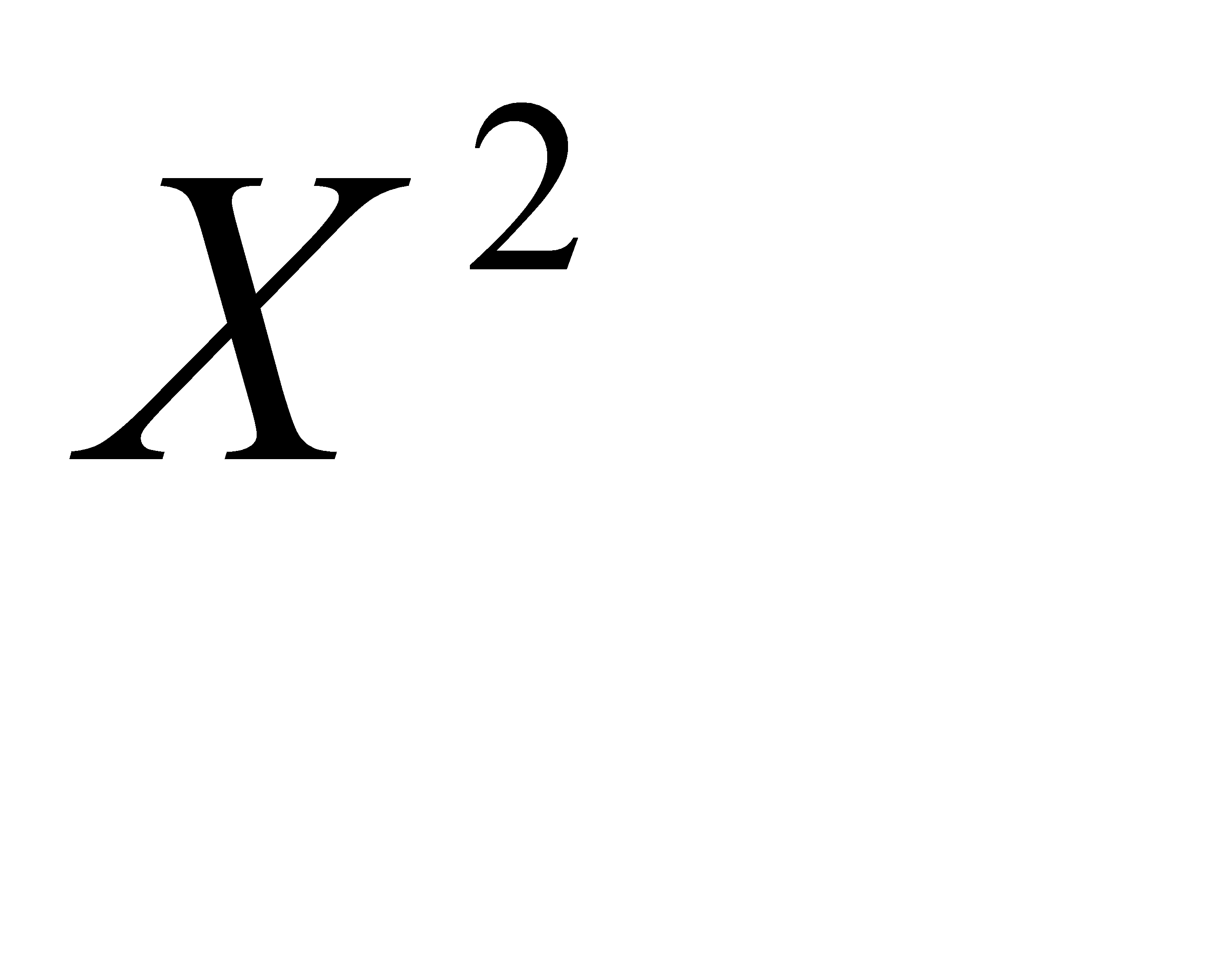 ;
;
 ,
,
Найдем дисперсию Х:
 .
.
#213
Найти дисперсию дискретной случайной величины X—числа появлений события А в пяти независимых испытаниях, если вероятность появления событий А в каждом испытании равна 0, 2.
Решение.
Дисперсия числа появлений события в независимых испытаниях (с одинаковой вероятностью появления события в каждом испытании) равна произведению числа испытаний на вероятности появления и непоявления события:
D(X) = npq.
По условию, n = 5; р = 0, 2; q = 1—0, 2 = 0, 8.
Искомая дисперсия
D(X) = npq = 5-0, 2- 0, 8 = 0, 8.
Ответ: 0, 8
#214
Найти дисперсию дискретной случайной величины Х – числа отказов элемента некоторого устройства в десяти независимых опытах, если вероятность отказа элемента в каждом опыте равна 0, 9.
Решение
Дисперсия числа появлений события в независимых испытаниях(с одинаковой вероятностью появления события в каждом испытании) равна произведению числа испытаний на вероятности появления и непоявления события:
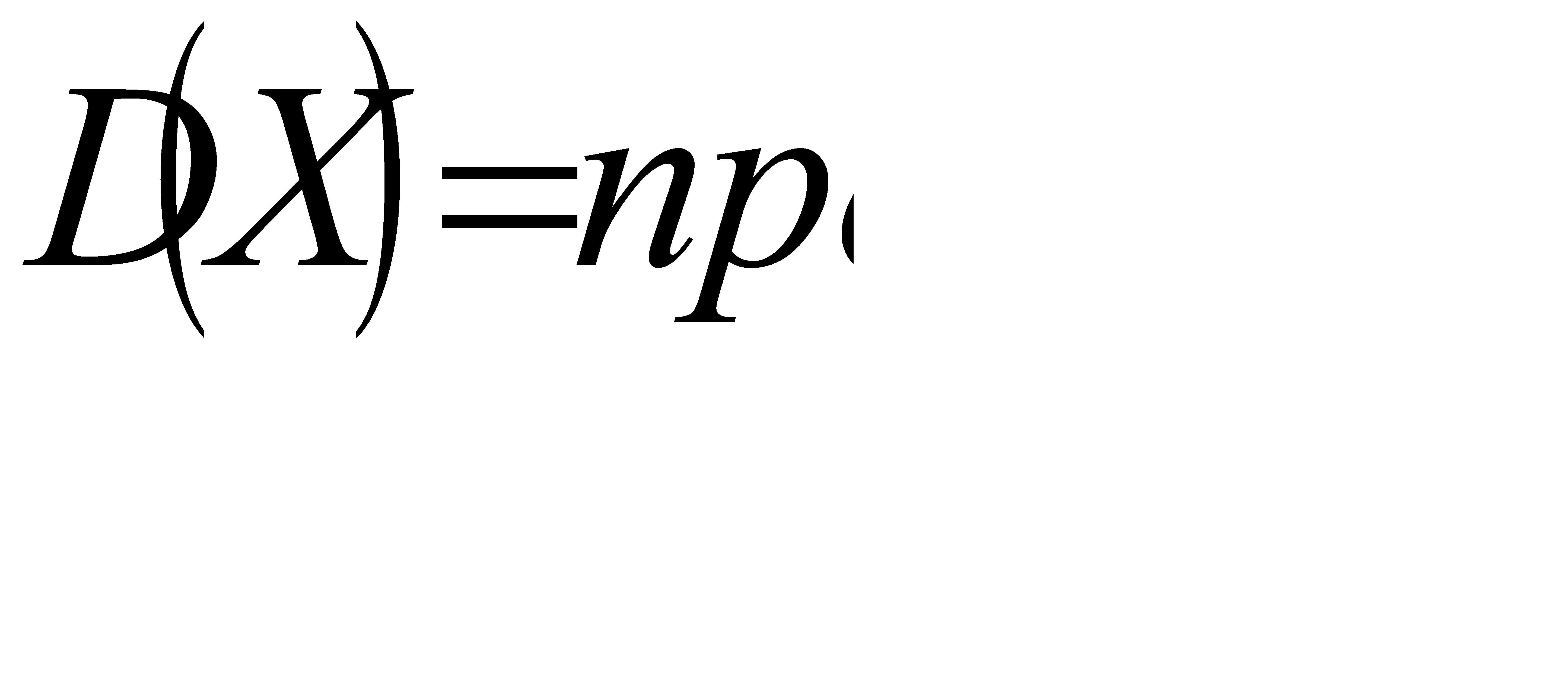 .
.
По условию, n = 10, p = 0, 9, q = 0, 1.
Искомая дисперсия

Ответ: 0, 9
#215
Задание: Найти дисперсию дискретной случайной величины 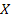 —числа появлений события
—числа появлений события 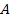 в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что
в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что 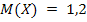 .
.
Решение. Первый способ: Возможные значения величины 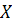 таковы:
таковы: 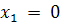 (событие не появилось),
(событие не появилось), 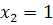 (событие появилось один раз) и
(событие появилось один раз) и 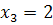 (событие появилось два раза).
(событие появилось два раза).
Найдем вероятности возможных значений по формуле Бернулли:
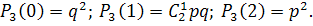
Напишем закон распределения 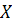 :
:
|
Найдём 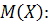
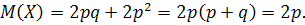
В силу условия 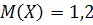 , т. е.
, т. е. 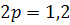 . Отсюда
. Отсюда 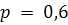 и, сле-
и, сле-
следовательно, 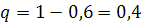 .
.
Искомая дисперсия
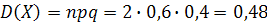
Второй способ: Воспользуемся формулой 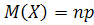 . По условию,
. По условию, 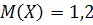 ;
; 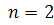 . Следовательно,
. Следовательно, 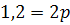 . Отсюда
. Отсюда 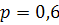 и, значит,
и, значит, 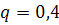 .
.
Найдем искомую дисперсию:
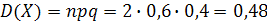
#216
Найти дисперсию дискретной случайной величины Х – числа появлений события А в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что М(Х)=0. 9.
Решение.
D(X)=npq
M(X)=np, n=2 => p=0. 45.
q=1-p=0. 55
D(X)=2*0. 45*0. 55=0. 495
Ответ: 0. 495.
#217
Производятся независимые испытания с одинаковой вероятностью появления события А в каждом испытании. Найти вероятность появления события А, если дисперсия числа появлений события в трех независимых испытаниях равна 0, 63.
Решение:
Дисперсия равна:
D(X)=npq=3*pq=0, 63
pq=0, 21
q=1-p
p-p2=0, 21
p2-p+0, 21=0
Решим квадратное уравнение.
Искомая вероятность появления события А равна:
p1=0, 7
p2=0, 3
#218
Сумма вероятностей всех возможных значений дискретной случайной величины равна единице, поэтому вероятность того, что Х примет значение х2, равна 1-0, 6=0, 4
Напишем закон распределения Х:
X x1 x2
P 0, 6 0, 4 {1}
Для отыскания x1 и x2 надо составить два уравнения, связывающие эти числа. С этой целью выразим известные математическое ожидание и дисперсию через x1 и x2
Найдём М(Х)
М(Х)=0, 6*x1+0, 4*x2
По условию, М(Х)=1, 4, следовательно
0, 6*x1+0, 4*x2=1, 4 {2}
Для того, чтобы получить второе уравнение, выразим известную дисперсию через x1 и x2
Напишем закон распределения Х2
Х2 
p 0, 6 0, 4
найдём М(Х2)
М(Х2)=0, 6* 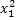 + 0, 4*
+ 0, 4* 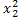
Найдём дисперсию
D(X)= М(Х2)-[ М(Х)]2=0, 6* 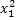 + 0, 4*
+ 0, 4* 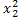 -1, 42
-1, 42
Подставляя D(X)=0, 24, после элементарных преобразований получим
0, 6* 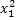 + 0, 4*
+ 0, 4* 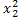 =2, 2 {3}
=2, 2 {3}
Объединяя {2} и {3}, получим систему уравнений
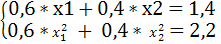
Решив эту систему, найдём 2 решения
x1=1, x2=2; x1=1, 8, x2=0, 8
По условию x2> x1, поэтому задаче удовлетворяет лишь первое решение x1=1, x2=2 {4}
Подставив {4} в {1}, получим искомый закон распределения
X 1 2
P 0, 6 0, 4
#219
Дискретная случайная величина X имеет только два возможных значения: x1 и x2, причем x1 < x2. Вероятность того, что X примет значение x1, равна 0, 2. Найти закон распределения X, зная математическое ожидание M(X)=2, 6 и среднее квадратическое отклонение σ (X)=0, 8.
Решение: Напишем закон распределения Х (вероятность х2 получим из формулы о сумме вероятностей всех возможных значений дискретной случайной величины):
| X | x1 | x2 |
| p | 0, 2 | 0, 8 |
Нам известно математическое ожидание, тогда:
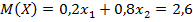
Так как 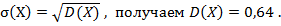 Т. е.
Т. е. 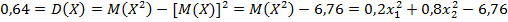 , отсюда
, отсюда 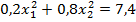
Объединяя, получим систему уравнений (умножим каждое на 5):
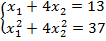
Решив систему, получим: 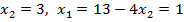
Ответ:
| X | ||
| p | 0, 2 | 0, 8 |
220....
#221
Брошены n игральных костей. Найти дисперсию суммы числа очков, которые могут появиться на всех выпавших гранях.
Решение: Обозначим через X дискретную случайную величину—сумму числа очков, которые выпадут на всех гранях, через 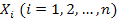 — число очков, выпавших на грани -й кости. Тогда
— число очков, выпавших на грани -й кости. Тогда
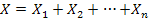
Очевидно, все величины X/ имеют одинаковое распределение, следовательно, одинаковые числовые характеристики и, в частности, одинаковые дисперсии, т. е.
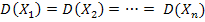 . (*)
. (*)
Так как рассматриваемые случайные величины независимы, то дисперсия их суммы равна сумме дисперсий слагаемых:
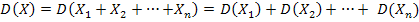 .
.
В силу (*) получим
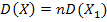 . (**)
. (**)
Таким образом, достаточно вычислить дисперсию случайной величины 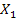 , т. е. дисперсию числа очков, которые могут выпасть на «первой» кости.
, т. е. дисперсию числа очков, которые могут выпасть на «первой» кости.
Напишем закон распределения 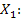
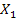
| ||||||
| p | 
| 
| 
| 
| 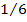
| 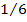
|
Найдем 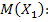
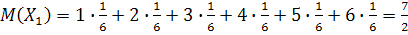
Напишем закон распределения 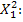
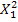
| ||||||
| p | 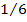
| 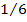
| 
| 
| 
| 
|
Найдем 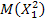 и
и 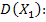
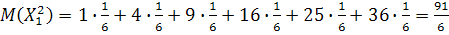
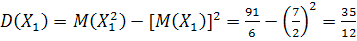 (***)
(***)
Найдем искомую дисперсию, для чего подставим (***) в (**):
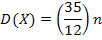
Ответ: 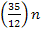 .
.
#222
Вероятность наступления события в каждом испытании равна p (0< p< 1). Испытания производятся до тех пор, пока событие не наступит. Найти:
А) математическое ожидание дискретной случайной величины X – числа испытаний, которые надо произвести до появления события;
Б) дисперсию величины X.
Решение.
А) Составим закон распределения величины X – числа испытаний, которые надо произвести, пока событие не наступит:
| X | … | k | … | |||
| p | p | qp | q2p | … | qk-1p | … |
Здесь q=1-p – вероятность не появления рассматриваемого события.
Найдем М(X):
M(X)=1*p+2*qp+3* q2p+…+k* qk-1p+…=p(1+2q+3 q2+…+kqk-1+…)=p* 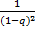 =
=  .
.
Итак, M(X)= 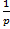 .
.
Б) Будем искать дисперсию величины X по формуле
D(X)=M(X2)-(M(X))2.
Учитывая, что M(X)= 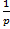 , получим D(X)= M(X2)-
, получим D(X)= M(X2)- 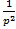 .
.
Остается найти M(X2). Напишем закон распределения X2, используя распределение
| X2 | … | k2 | … | |||
| p | p | qp | q2p | … | qk-1p | … |
Найдем M(X2):
M(X2)= 12*p+22*qp+32* q2p+…+ k2* qk-1p…=p(12+22q+32 q2+…+ k2* qk-1…)=p* 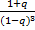 =
= 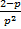 .
.
Итак, M(X2)= 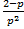 .
.
Найдем искомую дисперсию:
D(X)= 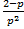 -
- 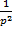 =
= 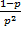 .
.
223....
#224
Доказать неравенство M[X-(xi+xk)/2]2≥ D(X), где xi и xk – любые два возможных значения случайной величины X.
Решение. 1) Допустим, что (xi+xk)/2=M(X). Тогда
M[X-(xi+xk)/2]2=D(X). (*)
2) Допустим, что -(xi+xk)/2≠ M(X). Докажем, что в этом случае
M[X-(xi+xk)/2]2> D(X)
Преобразуем левую часть неравенства, используя свойства математического ожидания:
M[X-(xi+xk)/2]2=M(X2)-2(xi+xk)/2 * M(X)+ [(xi+xk)/2]2.
Вычитая и прибавляя [M(X)]2 в правой части равенства, получим
M[X-(xi+xk)/2]2=D(X)+ [M(X)-(xi+xk)/2]2> D(X). (**)
Объединяя (*) и (**), окончательно имеем
M[X-(xi+xk)/2]2≥ D(X).
#225
Доказать, что если случайная величина X имеет наименьшее и наибольшее возможные значения, соответственно равные a и b, то дисперсия этой случайной величины не превышает квадрата полуразности между этими значениями:
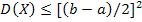 .
.
РЕШЕНИЕ.
Воспользуемся неравенством 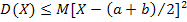 . Докажем теперь, что
. Докажем теперь, что
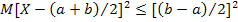 .
.
Очевидно, что из верности этого неравенства следует верность доказываемого. Преобразуем математическое ожидание: 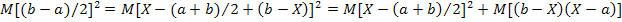 .
.
Второе слагаемое правой части равенства неотрицательно (т. к. b – наибольшее и a – наименьшее возможные значения), поэтому первое слагаемое не превышает всей суммы:
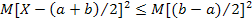 .
.
Так как математическое ожидание постоянной величины равно самой постоянной, то имеем
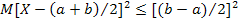 и
и 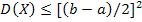 .
.
#226
Условие:
Доказать, что если 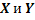 – две независимые случайные величины, то:
– две независимые случайные величины, то:
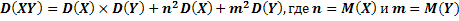
Решение:
Докажем по формуле для вычисления дисперсии.
Учитывая, что 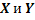 – независимые величины и, следовательно,
– независимые величины и, следовательно, 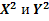 так же независимы и что математическое ожидание произведения случайных величин равно произведению их математических ожиданий, получим:
так же независимы и что математическое ожидание произведения случайных величин равно произведению их математических ожиданий, получим:
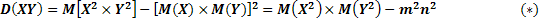
По определению дисперсии: 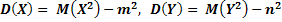
Отсюда: 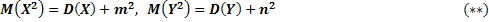
Подставив 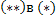 , после упрощения окончательно имеем:
, после упрощения окончательно имеем:
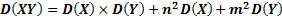
#236
Используя неравенство Чебышева, оценить вероятность того, что случайная величина X отклонится от своего математического ожидания менее чем на три средних квадратических отклонения.
Решение:
Ответ:
#237
Доказать неравенство Чебышева в форме .
Решение:
Так как события и
противоположные, то сумма их вероятностей равна единице. Т. е.,
#238
Используя неравенство Чебышева в форме, приведенной в задаче 237, оценить вероятность того, что случайная величина X отклонится от своего математического ожидания не меньше чем на два средних квадратических отклонения.
Решение:
Ответ:
#239
Используя неравенство Чебышева, оценить вероятность того, что , если D(X)= 0, 004.
Решение:
Ответ:
#240
Дано: и D(X) = 0, 009. Используя неравенство Чебышева, оценить ε снизу.
Решение:
#241
Устройство состоит из 10 независимо-работающих элементов. Вероятность отказа каждого элемента за время Т равна 0, 05. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время Т окажется:
а) меньше двух;
б) не меньше двух.
Решение:
а) Обозначим через X дискретную случайную величину - число отказавших элементов за время Т. Тогда
Воспользуемся неравенством Чебышева:
Подставив сюда М(Х)=0, 5; D(X) =0, 475, ε = 2, получим
б) События и
противопоположны, поэтому сумма их вероятностей равна единице. Следовательно,
#242
В осветительную сеть параллельно включено 20 ламп. Вероятность того, что за время Т лампа будет включена, равна 0, 8. Пользуясь неравенством Чебышева, оценить вероятность того, что абсолютная величина разности между числом включенных ламп и средним числом (математическим ожиданием) включенных ламп за время Т окажется:
а) меньше трех;
б) не меньше трех.
Решение:
а) Обозначим через X дискретную случайную величину - число отказавших элементов за время Т. Тогда
Воспользуемся неравенством Чебышева:
Подставив сюда М(Х)=16; D(X) =3. 2, ε = 3, получим
б) События и
противопоположны, поэтому сумма их вероятностей равна единице. Следовательно,
#243
Вероятность появления события А в каждом испытании равна ½. Используя неравенство Чебышева, оценить вероятность того, что число Х появлений события А заключено в пределах от 40 до 60, если будет произведено 100 независимых испытаний.
Решение.
Найдем математическое ожидание и дисперсию дискретной случайной величины Х – числа появлений события А в 100 независимых испытаниях:
М(Х) = n*p = 100* ½ = 50; D(X ) = n*p*q= 100* ½ * ½ =25.
Найдем максимальную разность между заданным числом появлений события и математическим ожиданием М(Х) = 50:
ε = 60 – 50 = 10.
Воспользуемся неравенством Чебышева в форме
Р( |Х – М(Х)|< ε ) ≥ 1 – D(X)/ε 2.
Подставляя М(Х) = 50, D(X) = 25, ε =10, получим
Р( |Х – 50|< 10) ≥ 1 – 25/102=0, 75.
#244
Вероятность появления события А в каждом испытании равна ¼ . Используя неравенство Чебышева, оценить вероятность того, что число Х появлений события А заключено в пределах от 150 до 250, если будет произведено 800 независимых испытаний.
Решение.
Найдем математическое ожидание и дисперсию дискретной случайной величины Х – числа появлений события А в 800 независимых испытаниях:
М(Х) = n*p = 800* ¼ = 200; D(X ) = n*p*q= 800* ¼ * ¾ =150.
Найдем максимальную разность между заданным числом появлений события и математическим ожиданием М(Х) = 200:
ε = 250 – 200 = 10.
Воспользуемся неравенством Чебышева в форме
Р( |Х – М(Х)|< ε ) ≥ 1 – D(X)/ε 2.
Подставляя М(Х) = 200, D(X) = 150, ε =50, получим
Р( |Х – 200|< 50) ≥ 1 – 150/502 = 1 – 0, 06 = 0, 94.
#245
Дискретная случайная величина X задана законом распределения
X 0, 3 0, 6
р 0, 2 0, 8
Используя неравенство Чебышева, оценить вероятность
того, что |Х — М(Х)|< 0, 2.
Решение:
Найдем математическое ожидание и дисперсию величины X:
M(X)=0, 3  0, 2 + 0, 6
0, 2 + 0, 6  0, 8=0, 54
0, 8=0, 54
D(X)=M(X2)-[M(X)]2= (0, 32  0, 2+0, 62
0, 2+0, 62  0, 8) – 0, 542 =0, 0144.
0, 8) – 0, 542 =0, 0144.
Воспользуемся неравенством Чебышева в форме
Р (| Х — М (X) | < 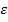 ) ≥ 1-D (Х)/
) ≥ 1-D (Х)/ 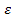 2
2
Подставляя М(Х)=0, 54, D(X) =0, 0144, 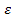 =0, 2, окончательно
=0, 2, окончательно
получим
Р (| X- 0, 54| < 0, 2) ≥ 1 -0, 0144/0, 04 =0, 64.
#246
Дискретная случайная величина X задана законом
распределения
X 0, 1 0, 4 0, 6
р 0, 2 0, 3 0, 5
Используя неравенство Чебышева, оценить вероятность
того, что |Х — М(Х)|< 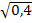
Решение:
Найдем математическое ожидание и дисперсию величины X:
M(X)=0, 1  0, 2 + 0, 4
0, 2 + 0, 4  0, 3+0, 6
0, 3+0, 6  0, 5 = 0, 44
0, 5 = 0, 44
D(X)=M(X2)-[M(X)]2= (0, 12  0, 2 + 0, 42
0, 2 + 0, 42 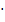 0, 3+0, 62
0, 3+0, 62  0, 5) – 0, 442 =0, 0364.
0, 5) – 0, 442 =0, 0364.
Воспользуемся неравенством Чебышева в форме
Р (| Х — М (X) | < 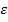 ) ≥ 1-D (Х)/
) ≥ 1-D (Х)/ 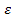 2
2
Подставляя М(Х)=0, 44, D(X) =0, 0364, 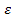 =
= 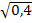 окончательно
окончательно
получим
Р (| X- 0, 44| < 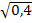 ) ≥ 1 -0, 0364/0, 4 =0, 909.
) ≥ 1 -0, 0364/0, 4 =0, 909.
#247
Последовательность независимых случайных величин 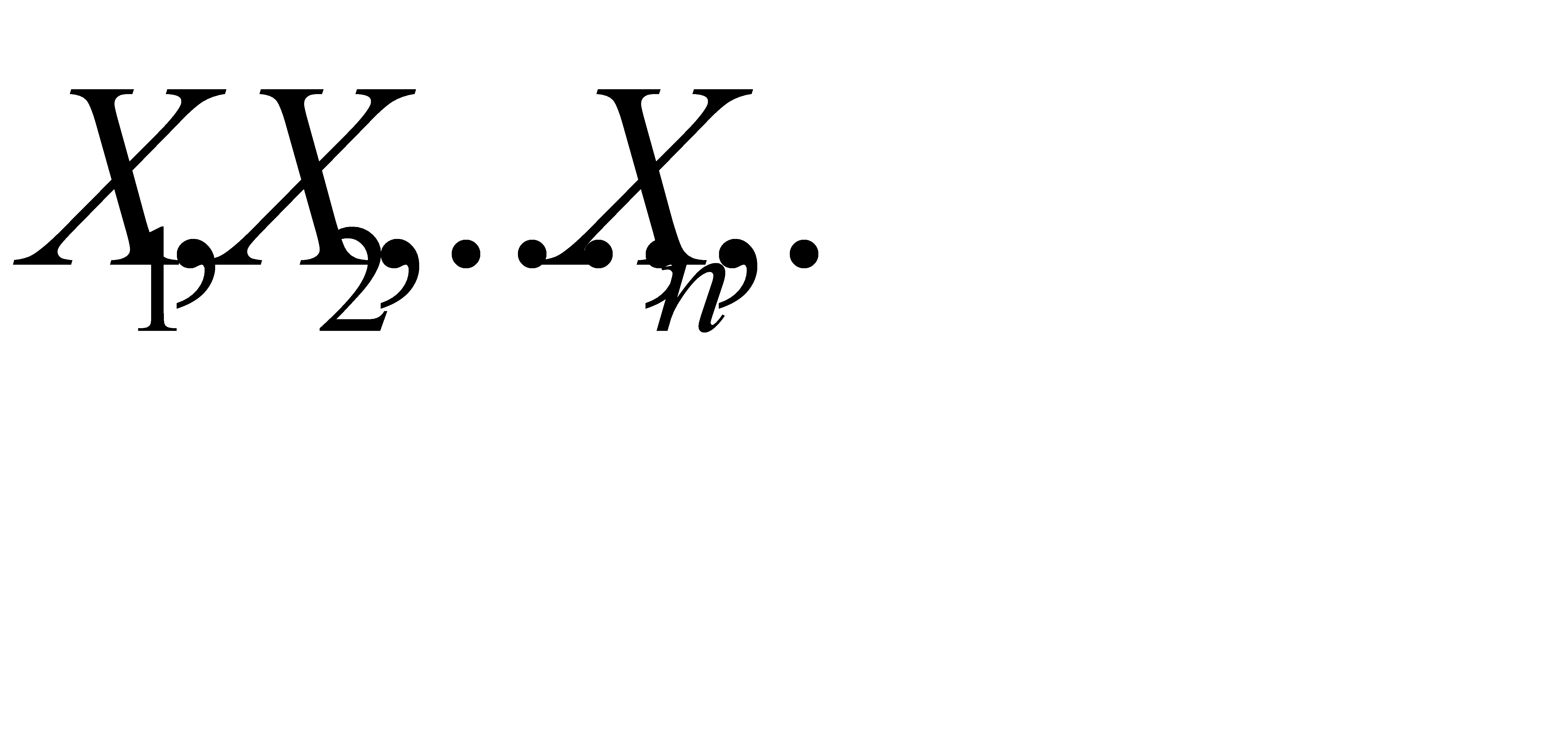 задана законом распределения
задана законом распределения
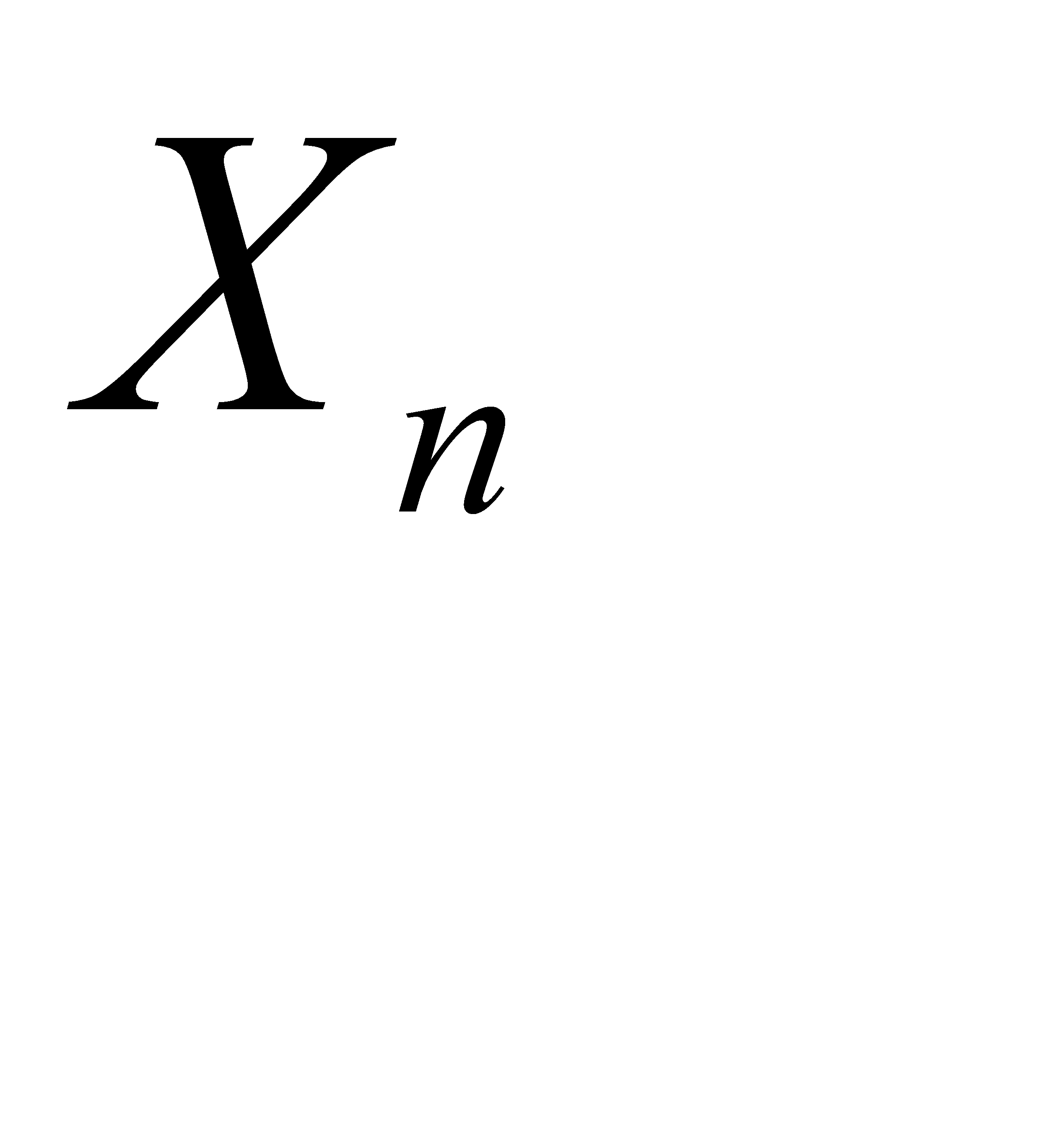
| 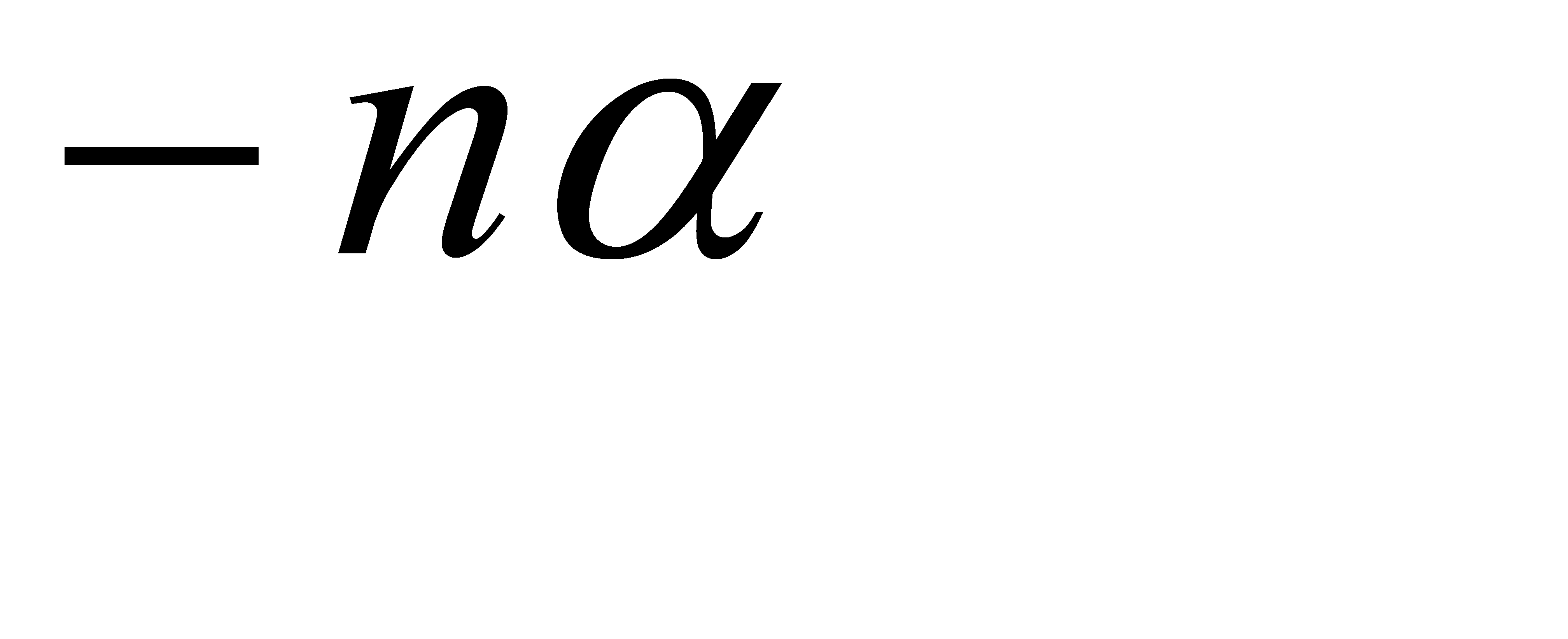
| 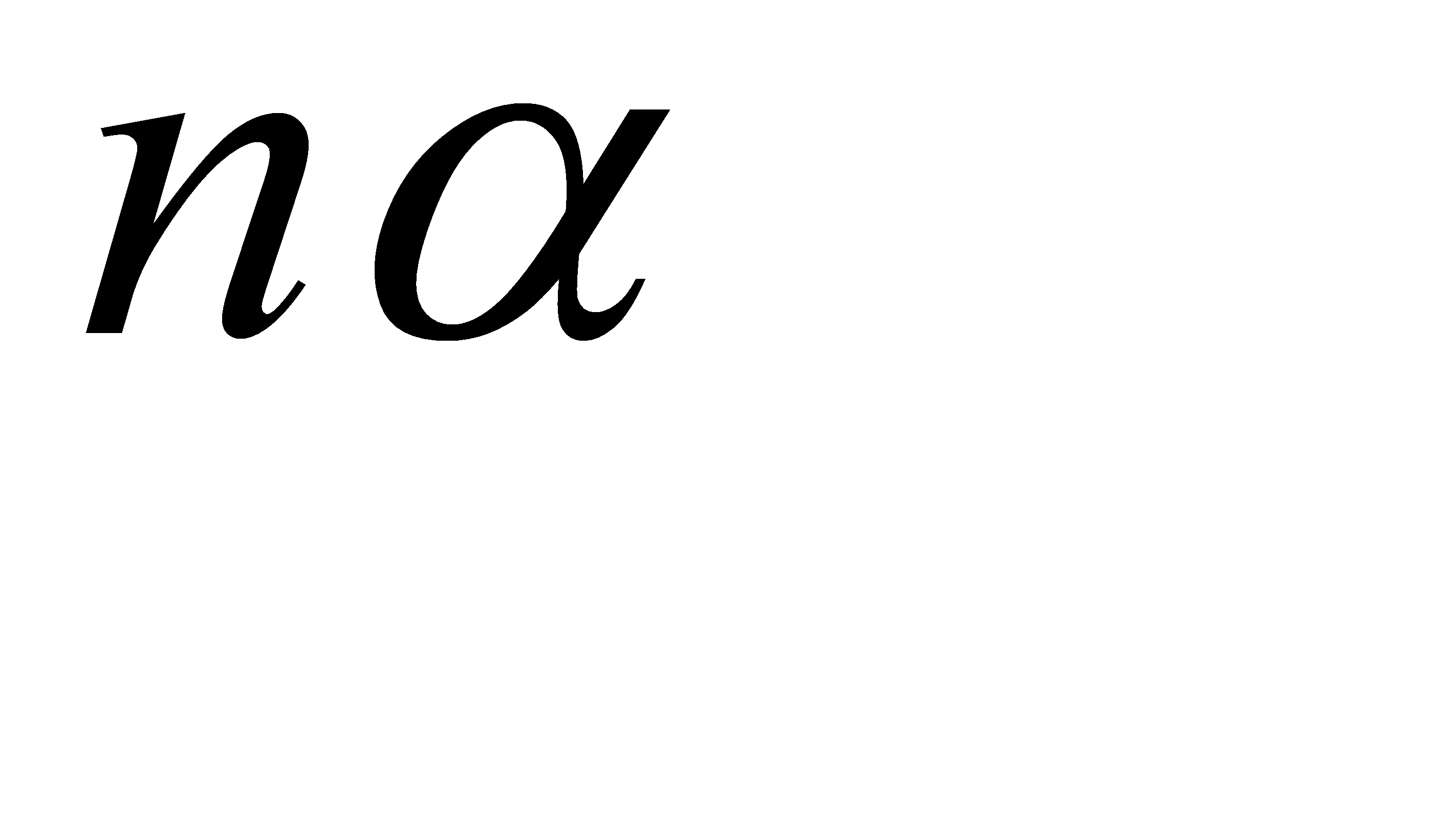
| |
| p | 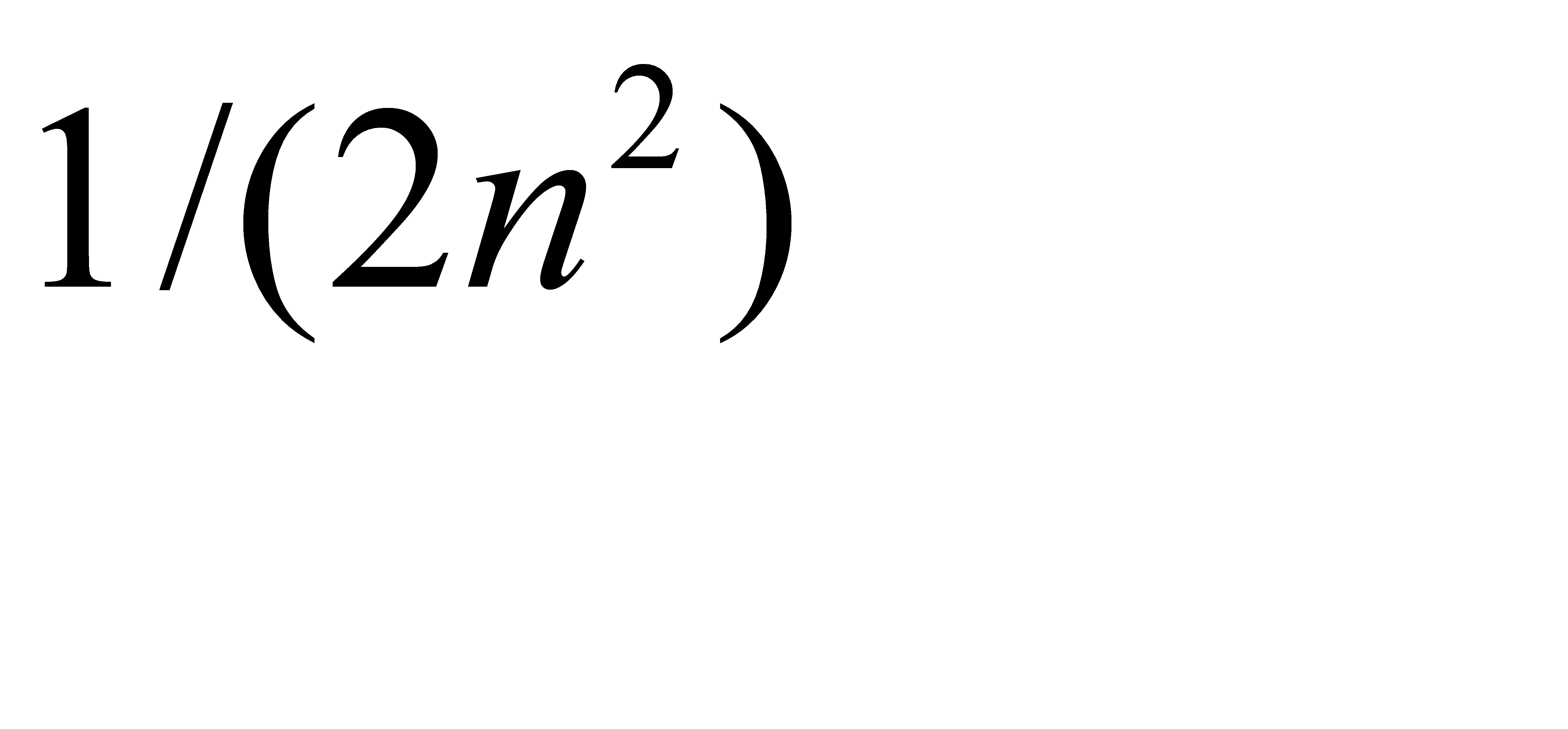
| 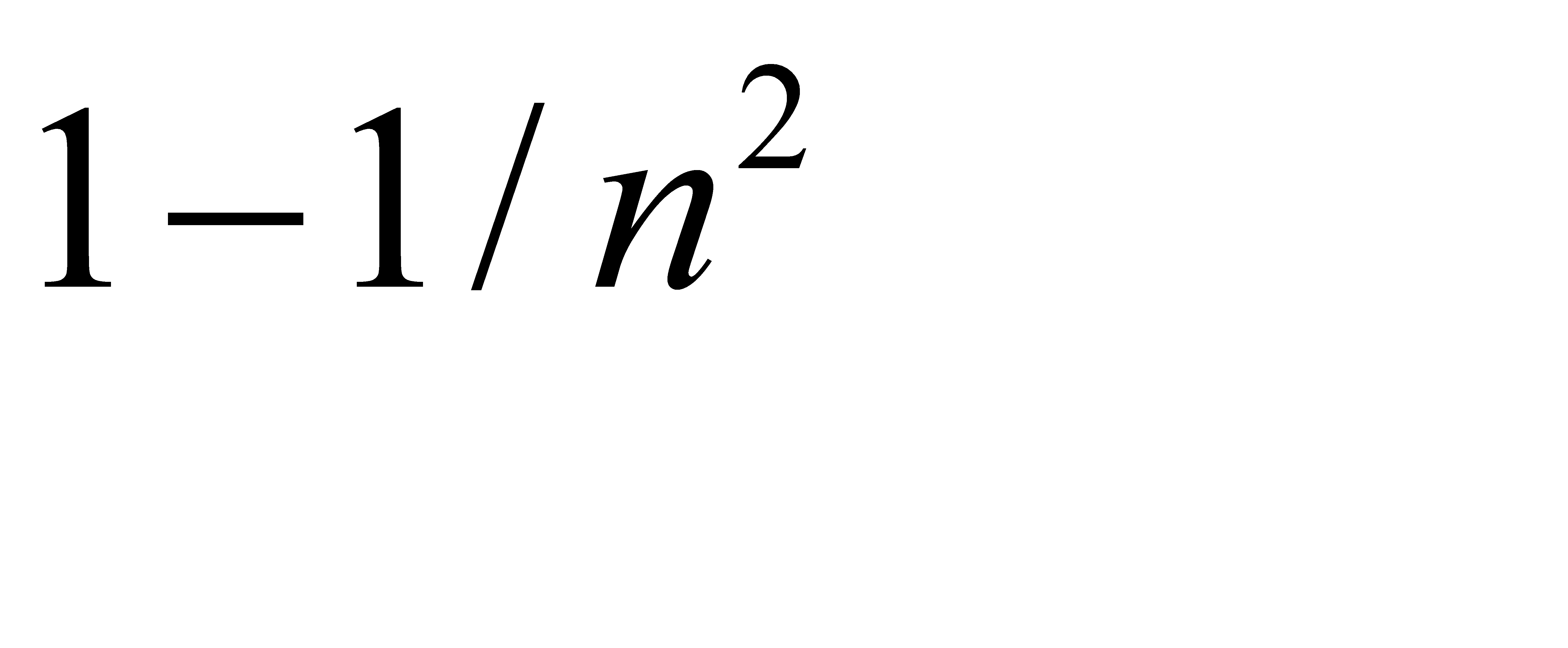
| 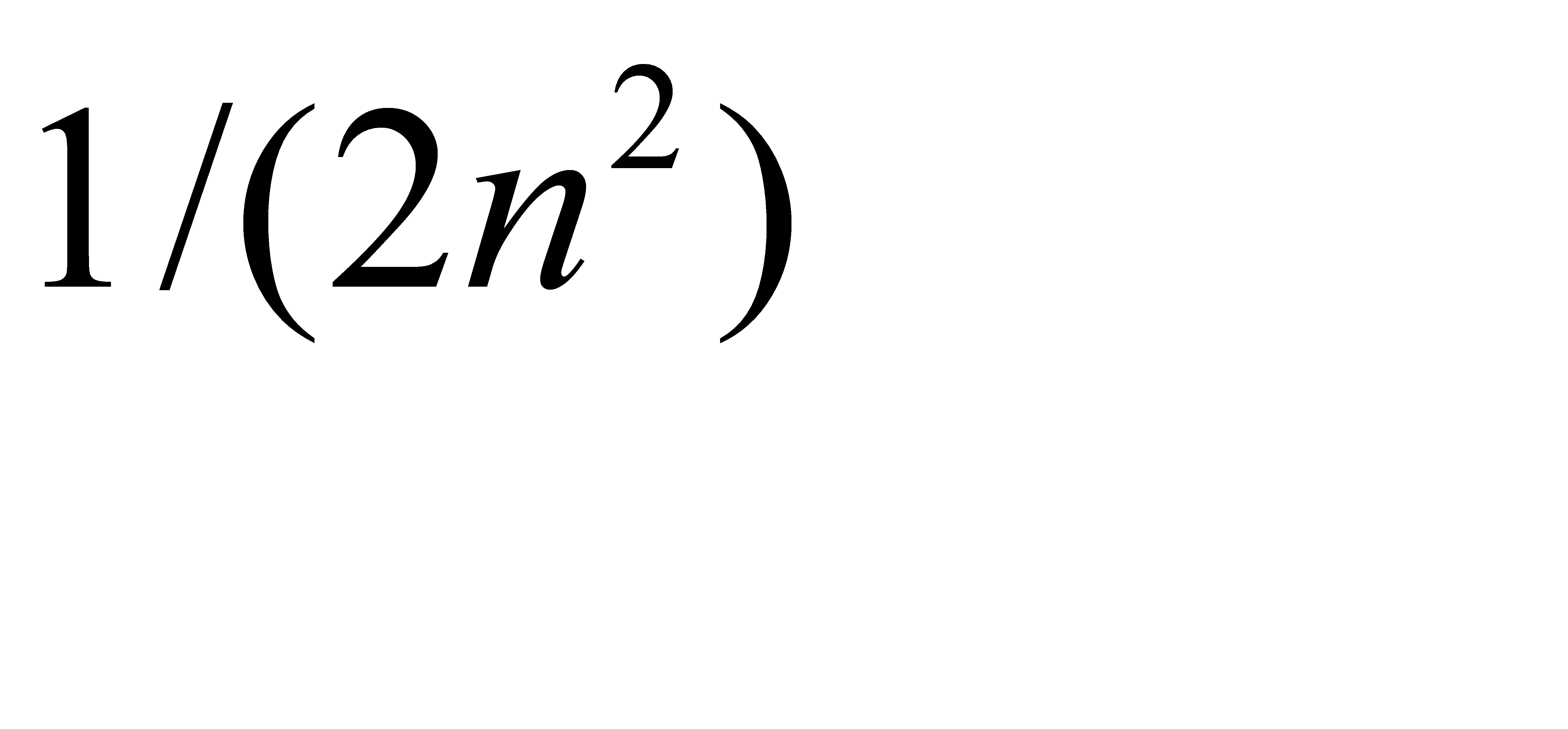
|
Применима ли к заданной последовательности теорема Чебышева?
Решение:
Для того, чтобы к последовательности случайных величин была применимы теорема Чебышева, достаточно, чтобы
1) эти величины были попарно независимы,
2) имели конечные математические ожидания,
3) имели равномерно ограниченные дисперсии.
Поскольку случайные величины независимы, то они подавно попарно независимы, т. е. первое требование теоремы Чебышева выполняется.
Проверим, выполняется ли требование конечности математических ожиданий:

Таким образом, каждая случайная величина имеет конечное (равное нулю) математическое ожидание, т. е. второе требование теоремы выполняется.
Проверим, выполняется ли требование равномерной ограниченности дисперсии. Напишем закон распределения 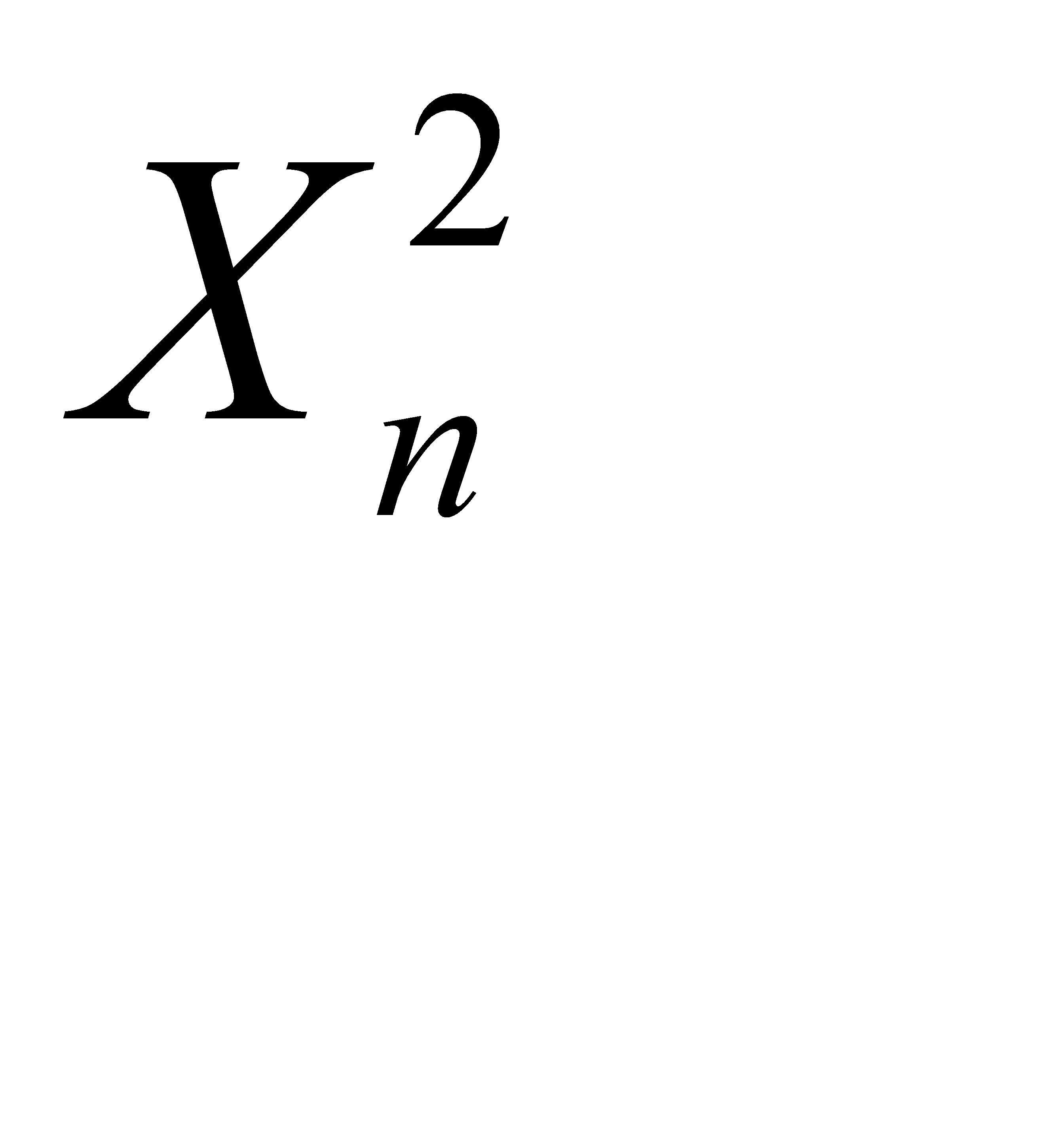 :
:
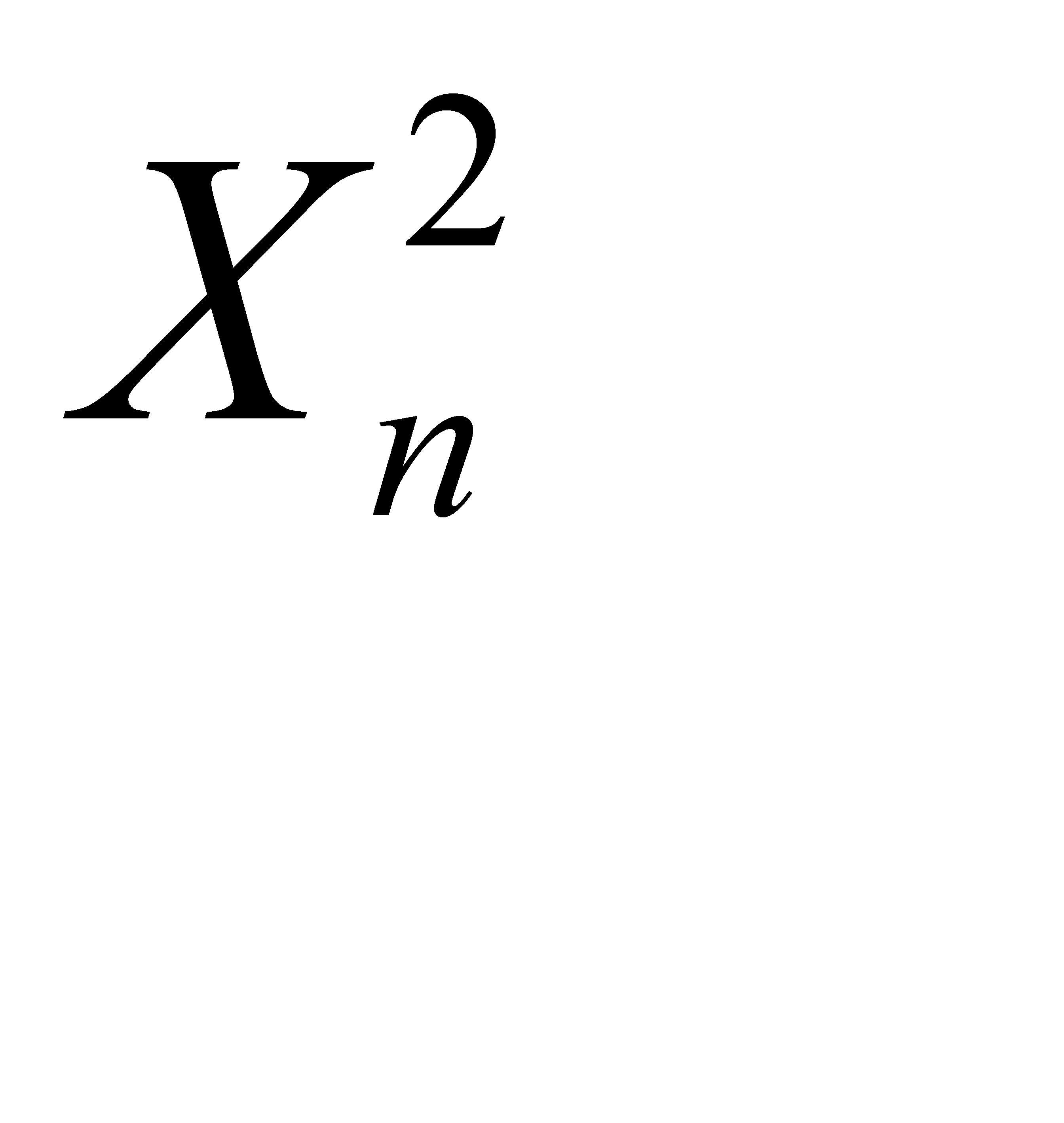
| 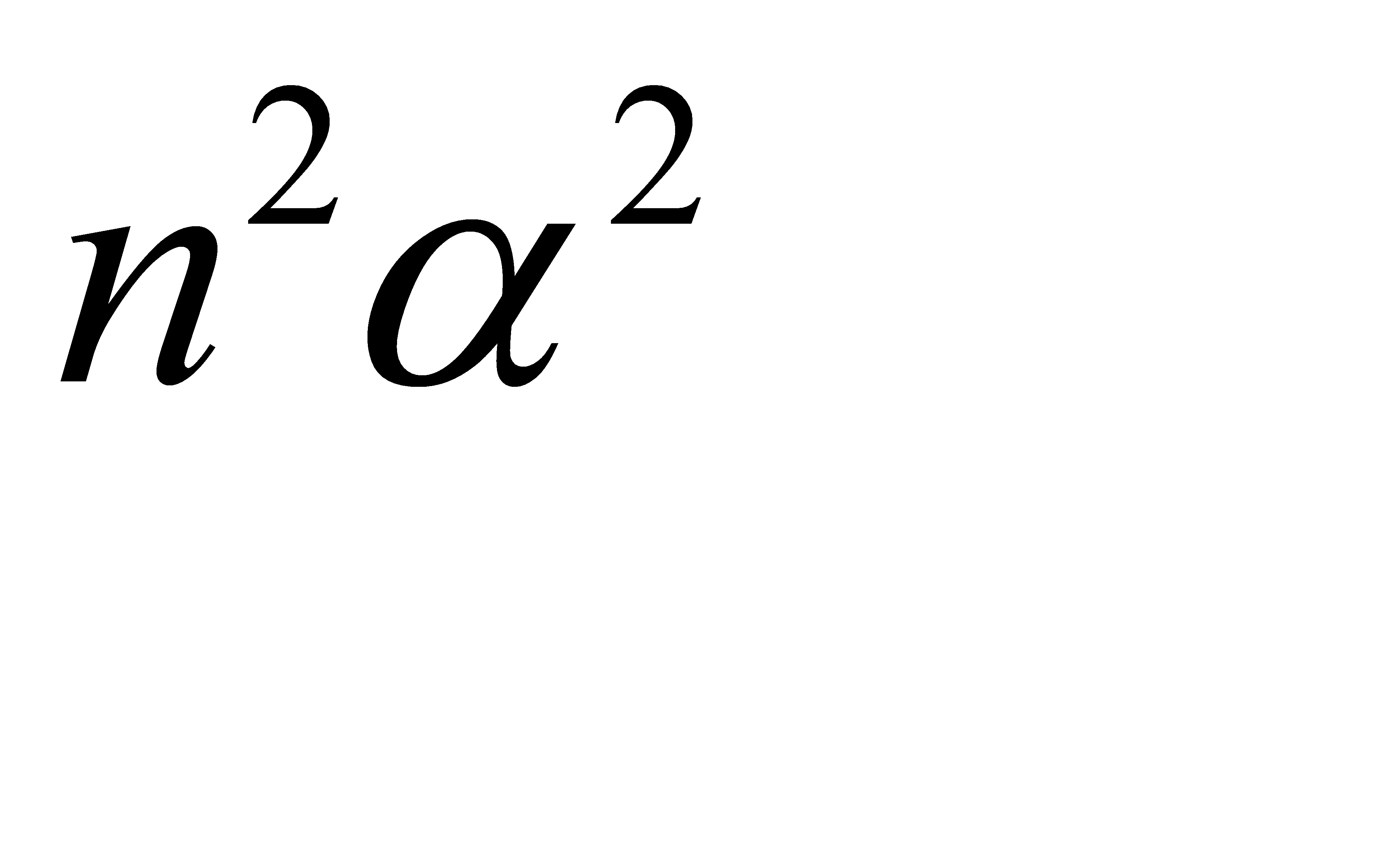
| 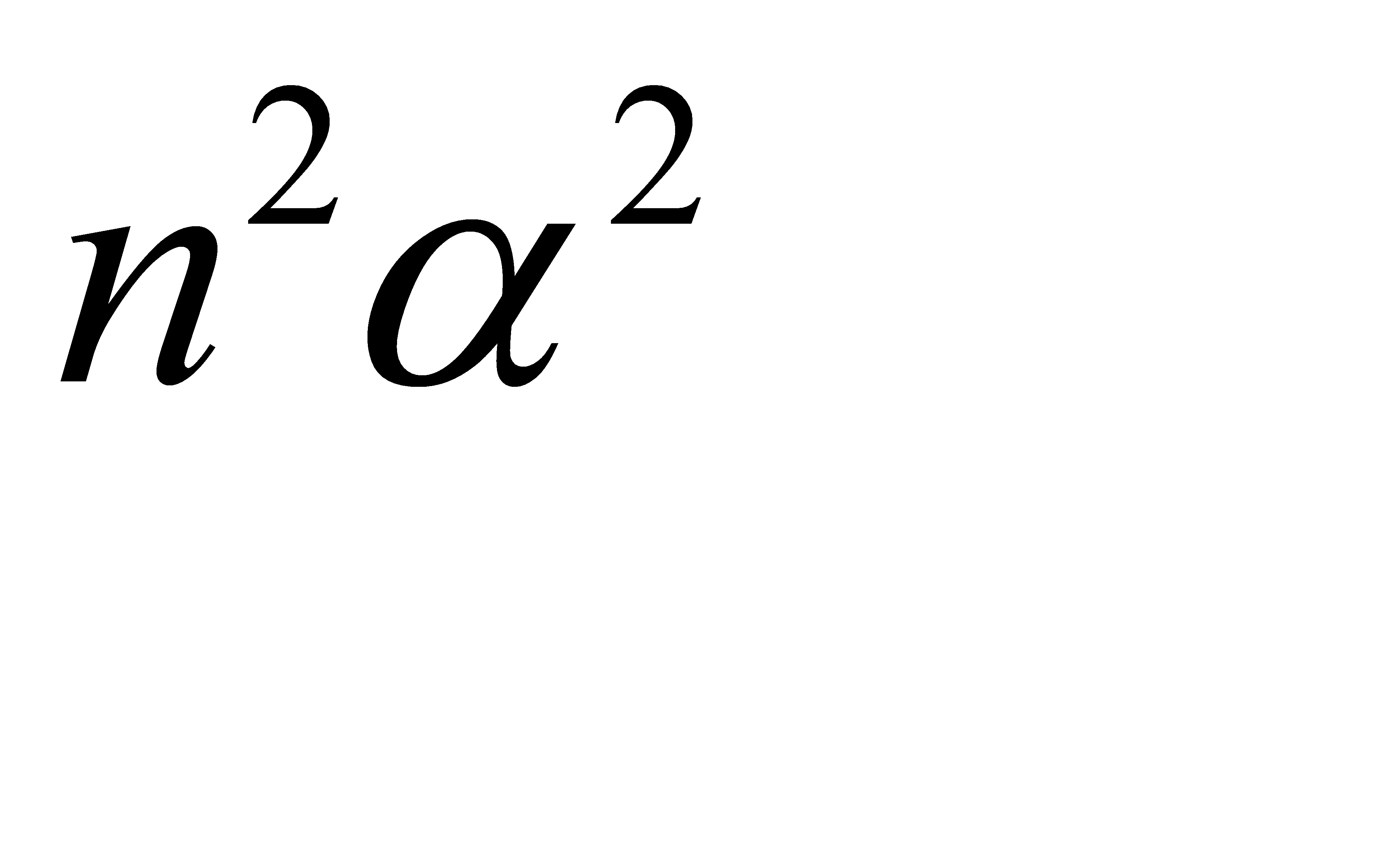
| |
| p | 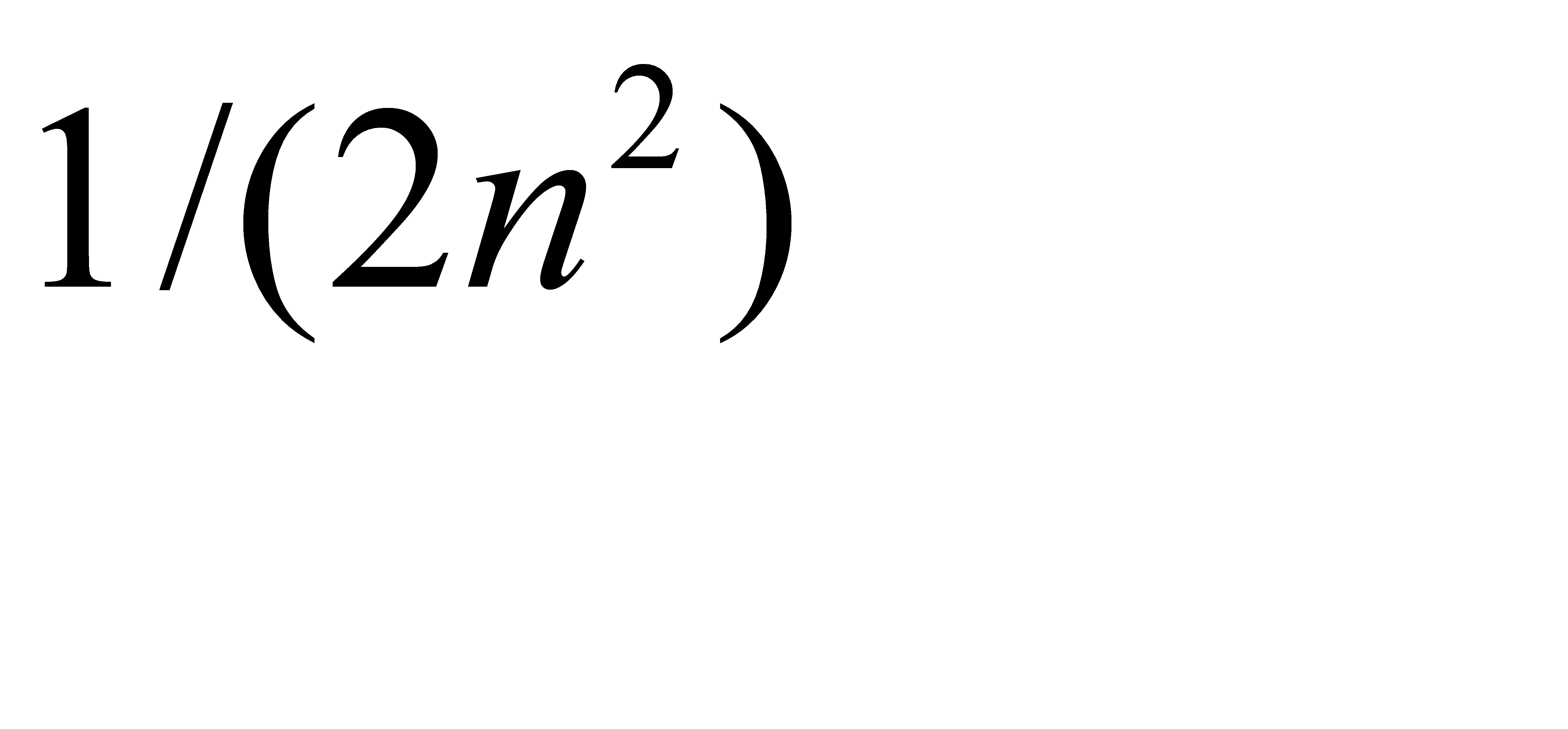
| 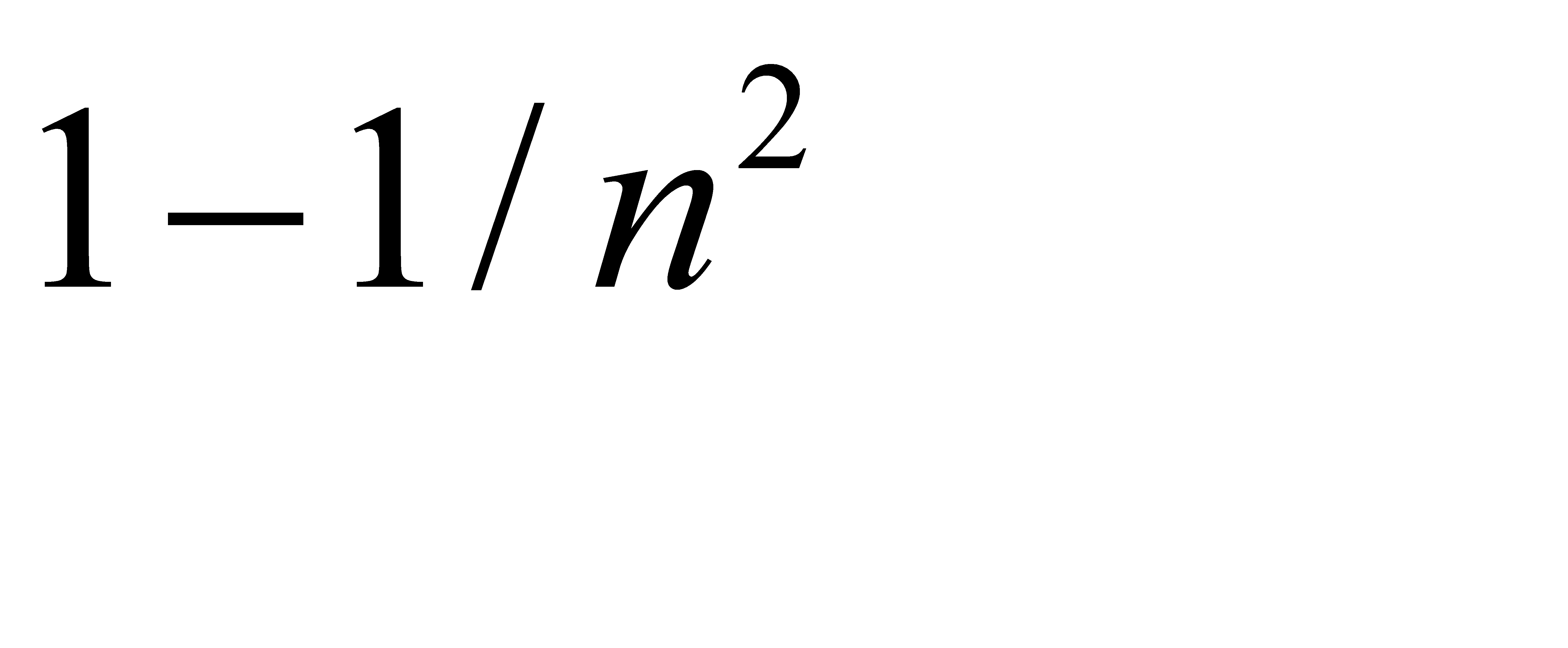
| 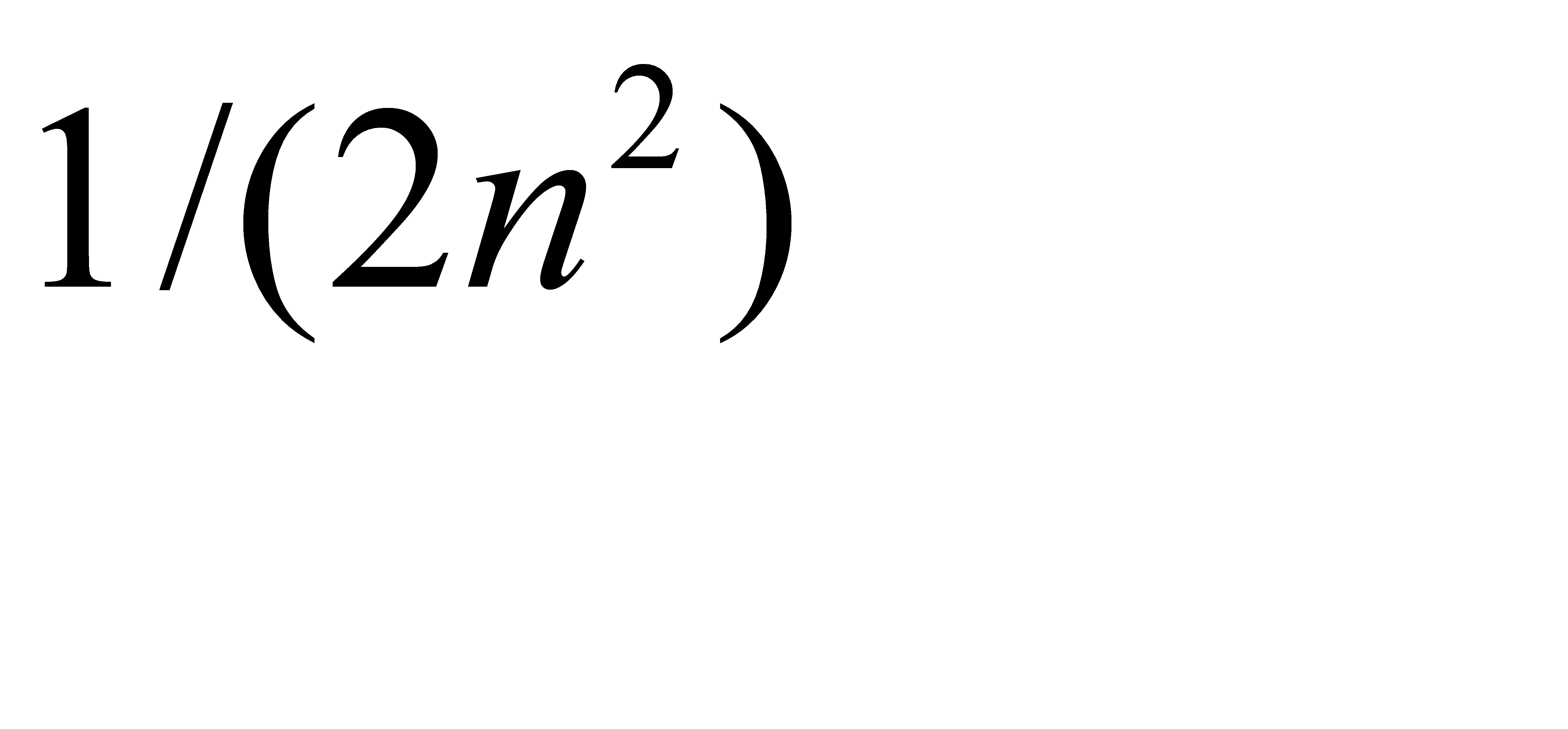
|
или, сложив вероятности одинаковых возможных значений,
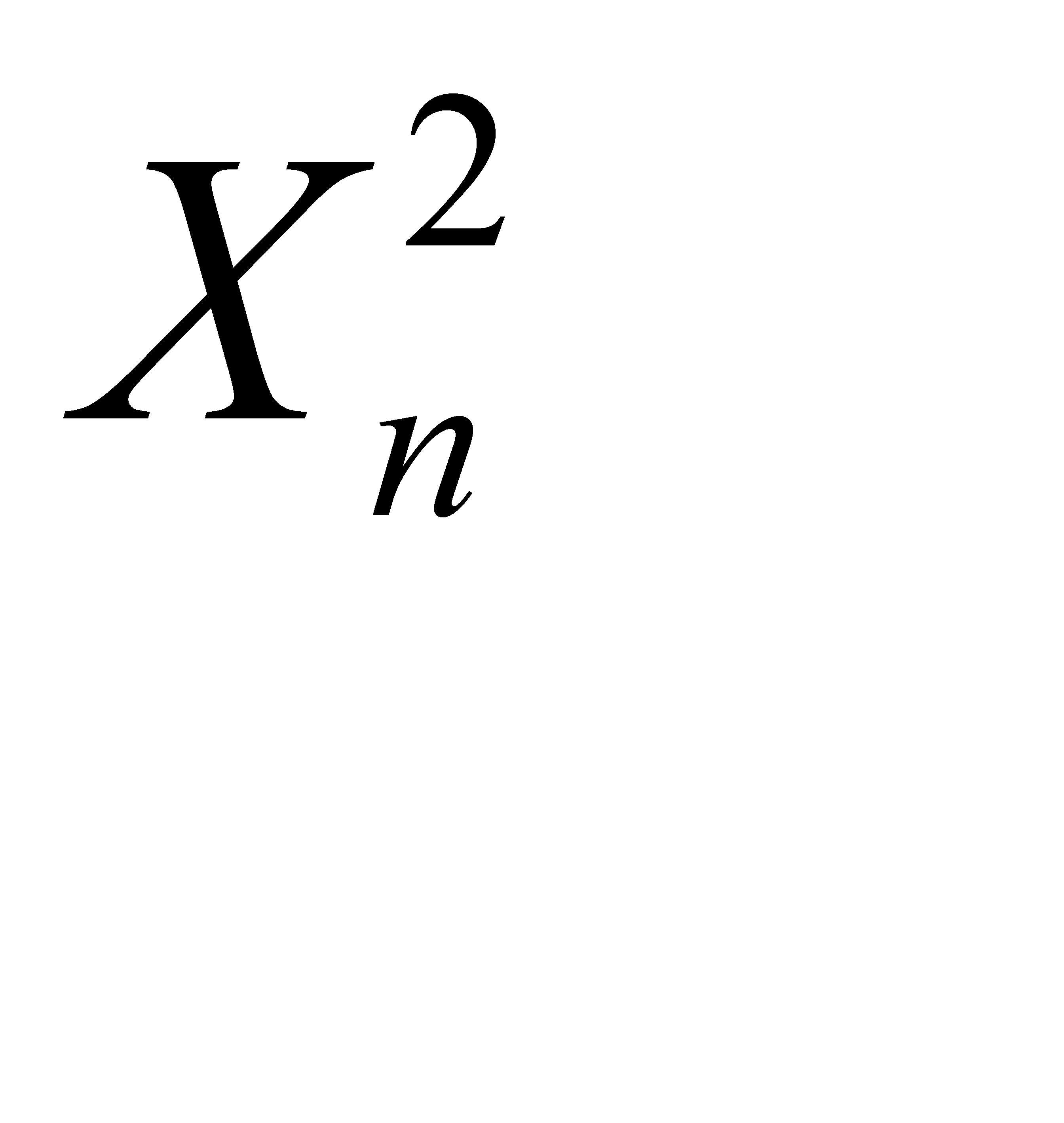
| 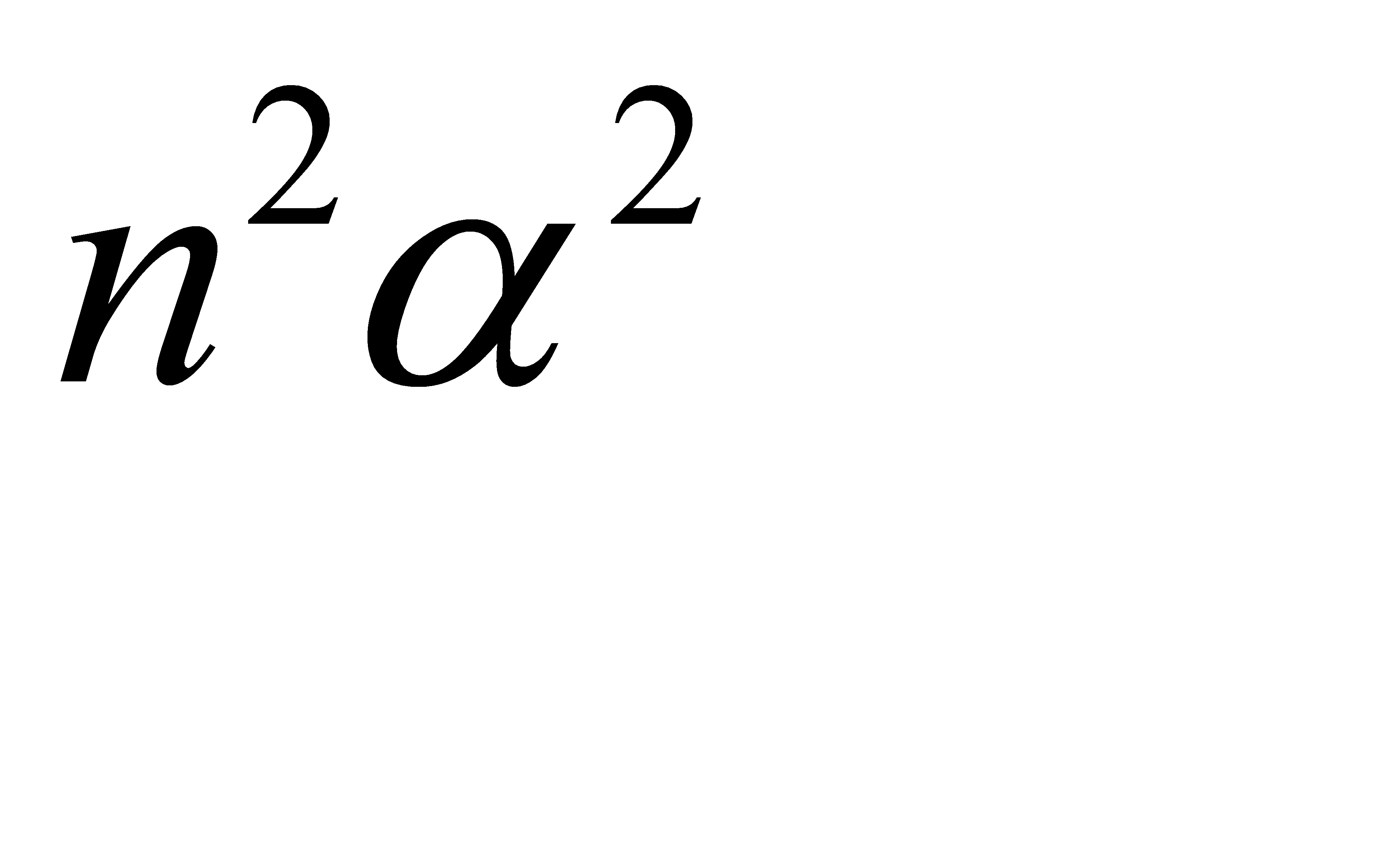
| |
| p | 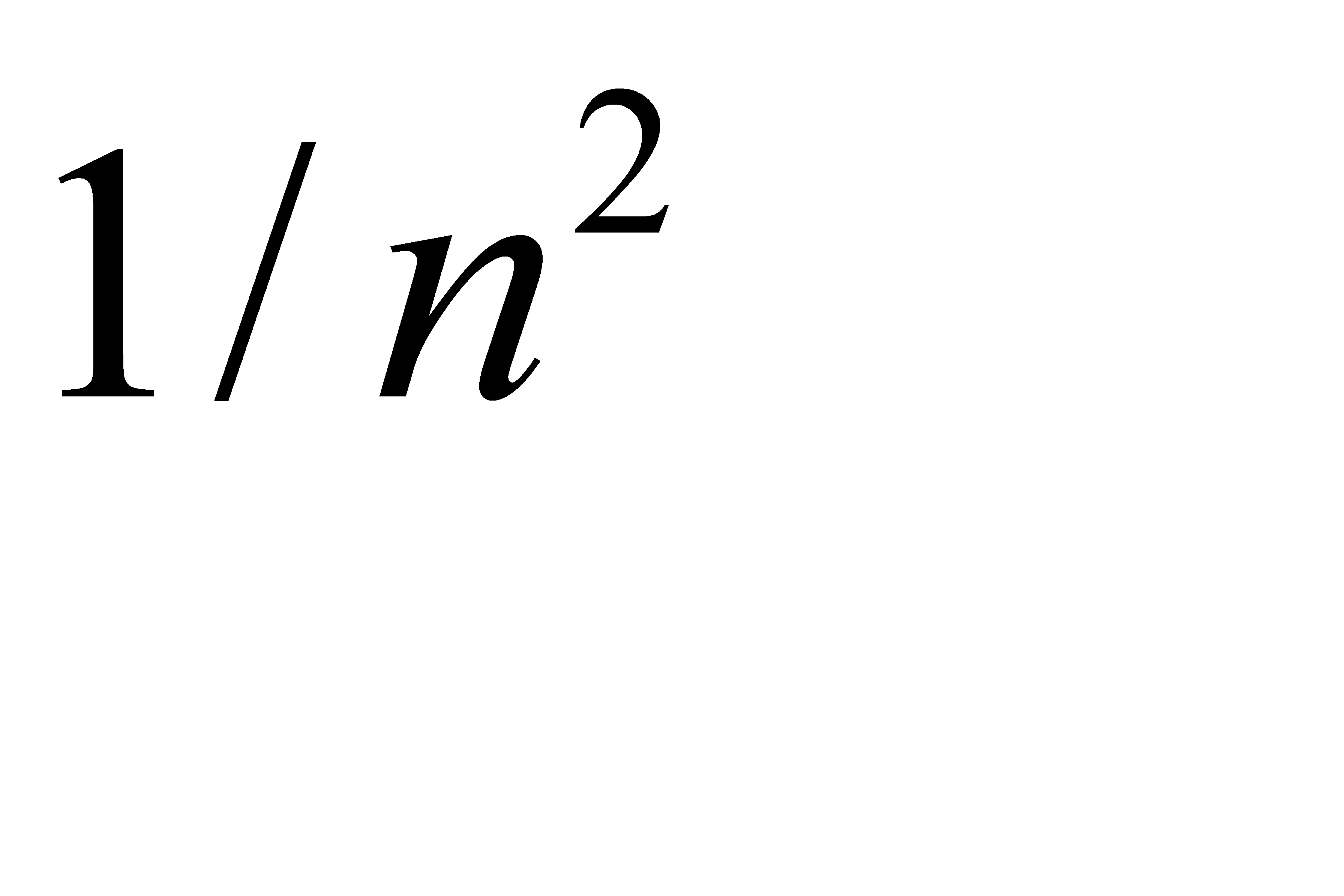
| 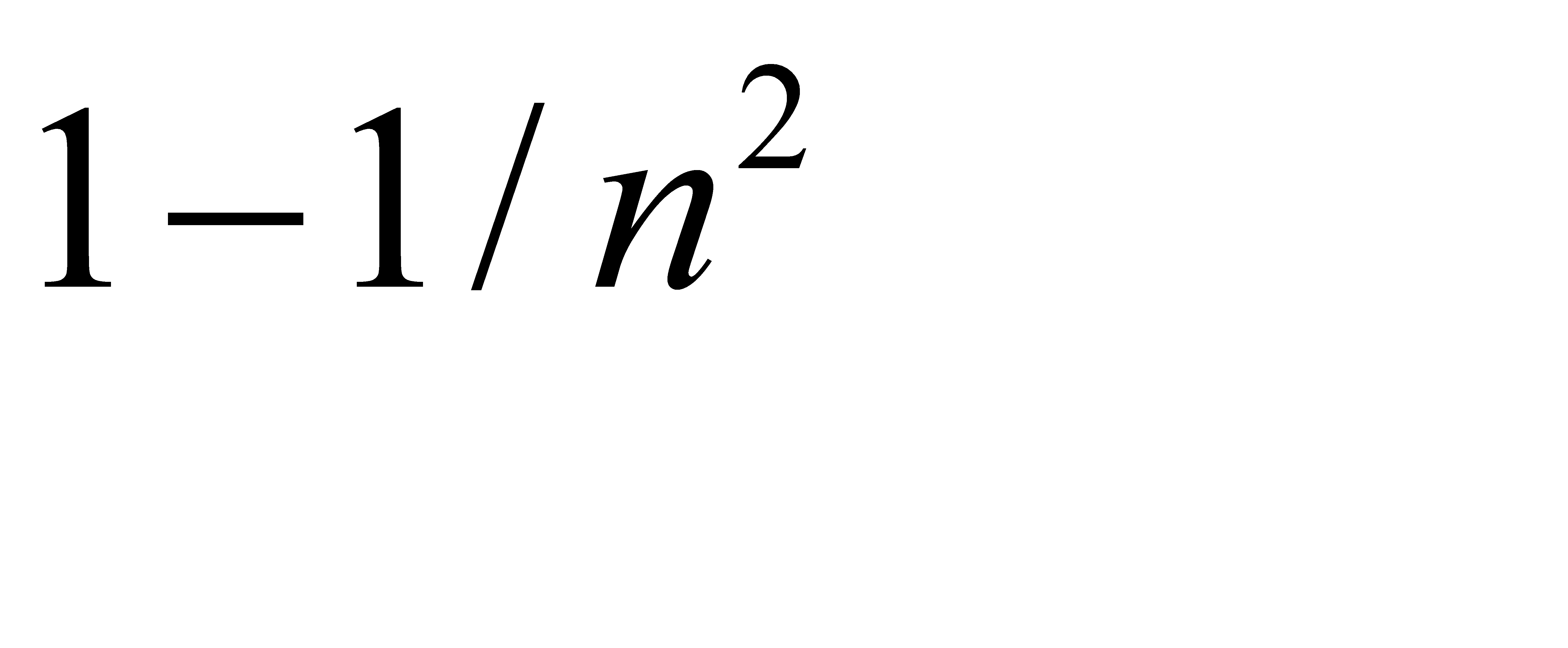
|
Найдём математическое ожидание 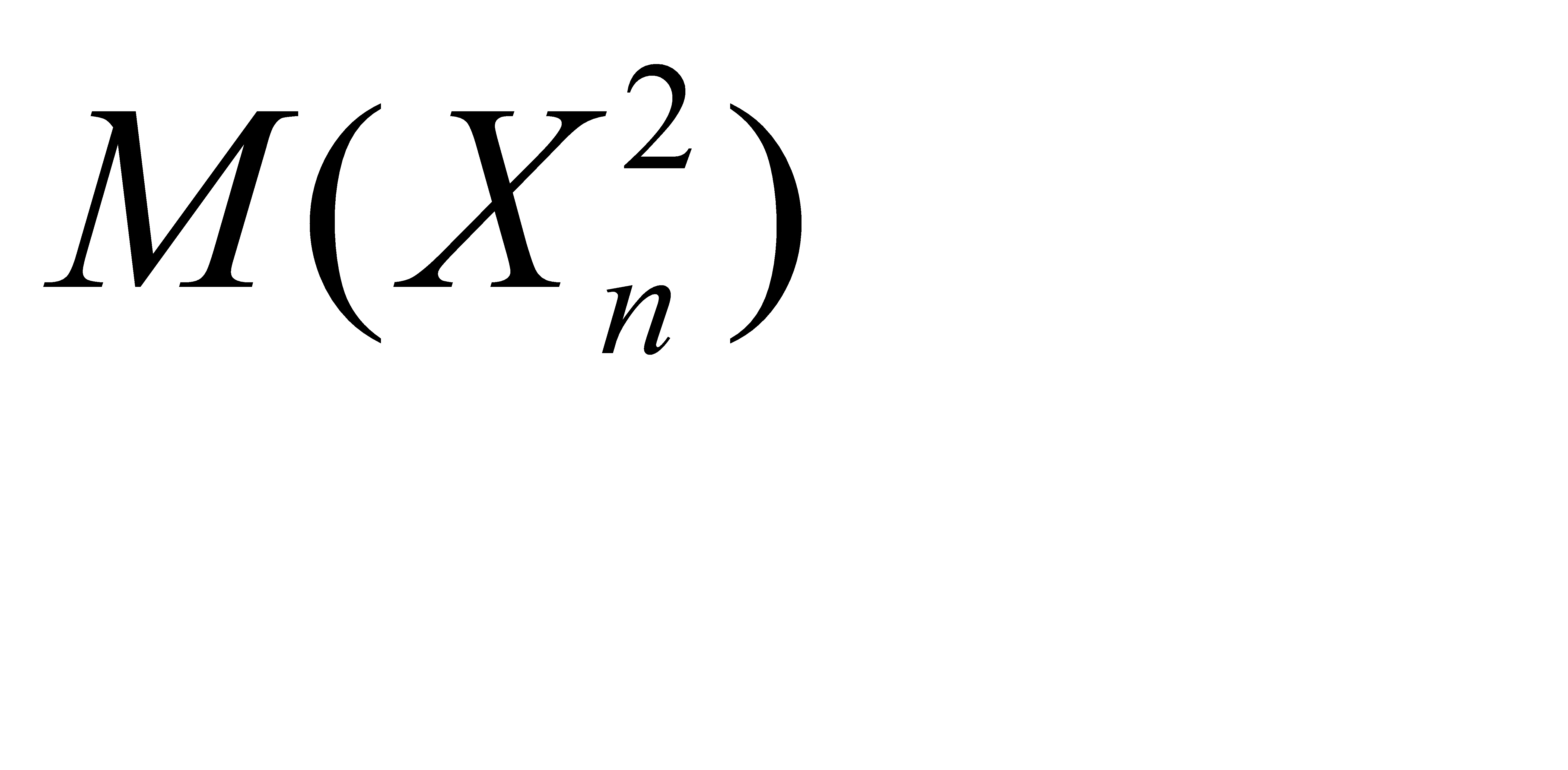 :
:
Найдём дисперсию 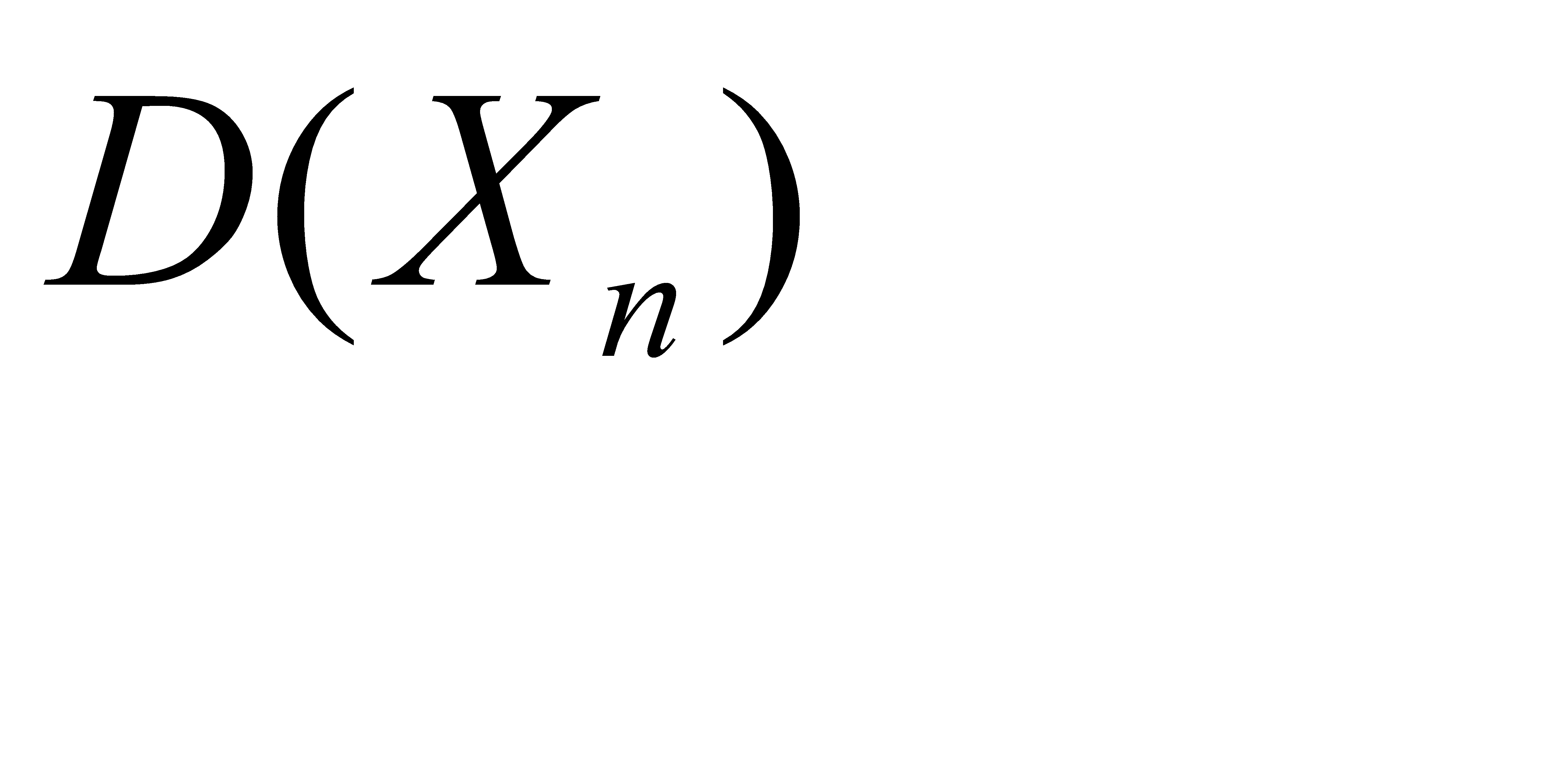 :
:
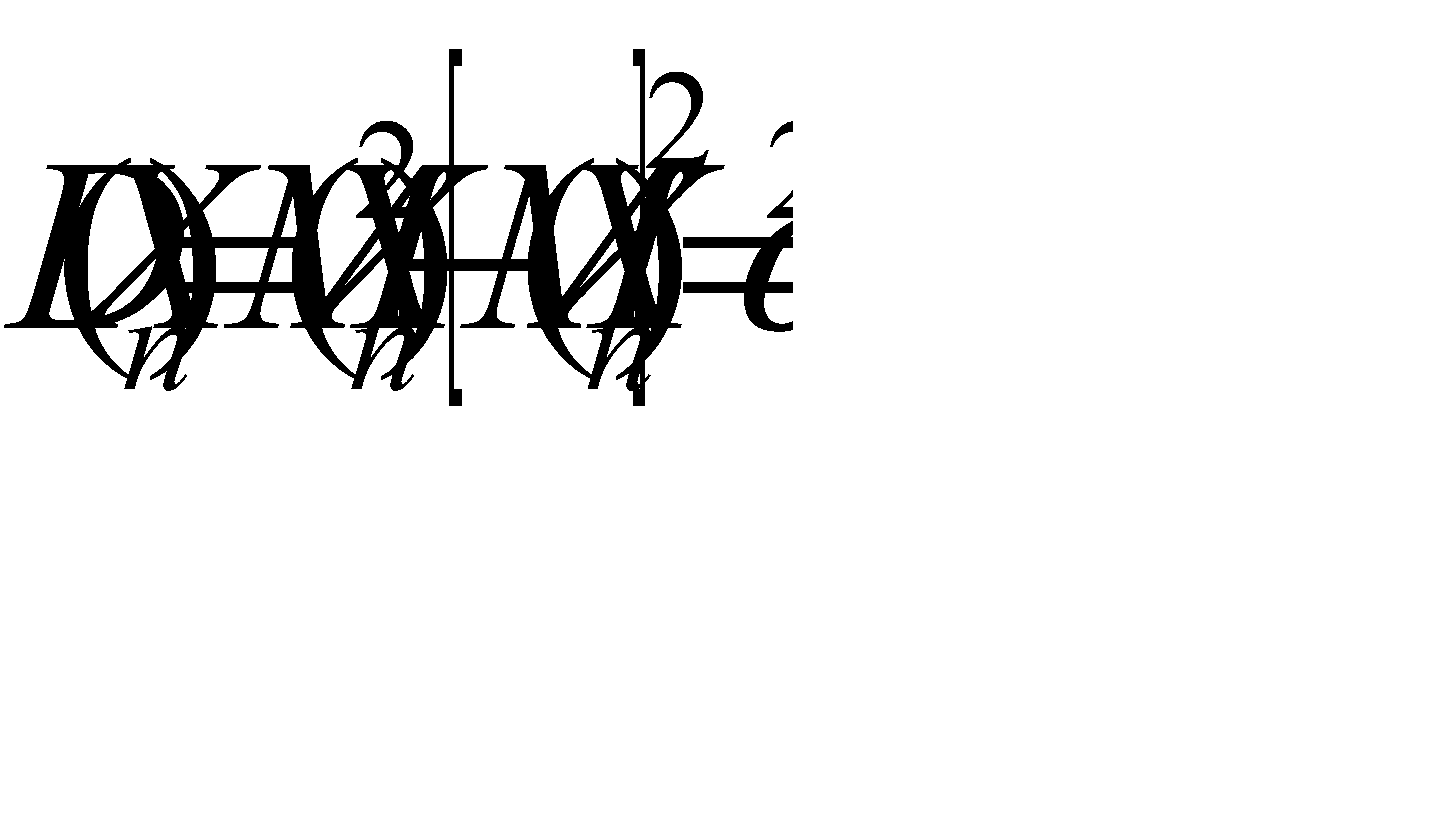
Таким образом, дисперсии заданных случайных величин равномерно ограничены
числом 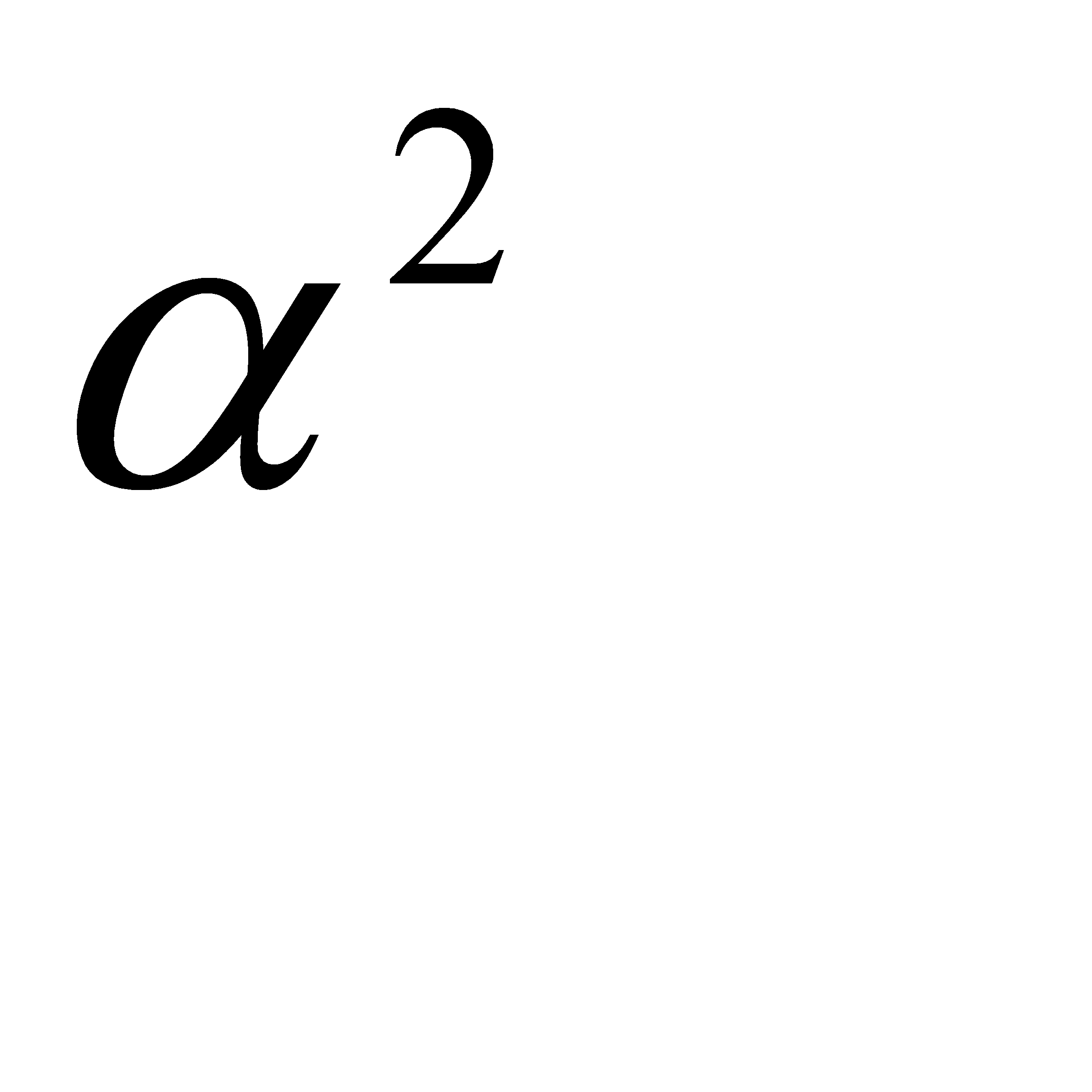 , т. е. третье требование выполняется.
, т. е. третье требование выполняется.
Итак, поскольку все требования выполняются, к рассматриваемой последовательности случайных величин теорема Чебышева применима.
Ответ: применима.
#248
Последовательность независимых случайных величин 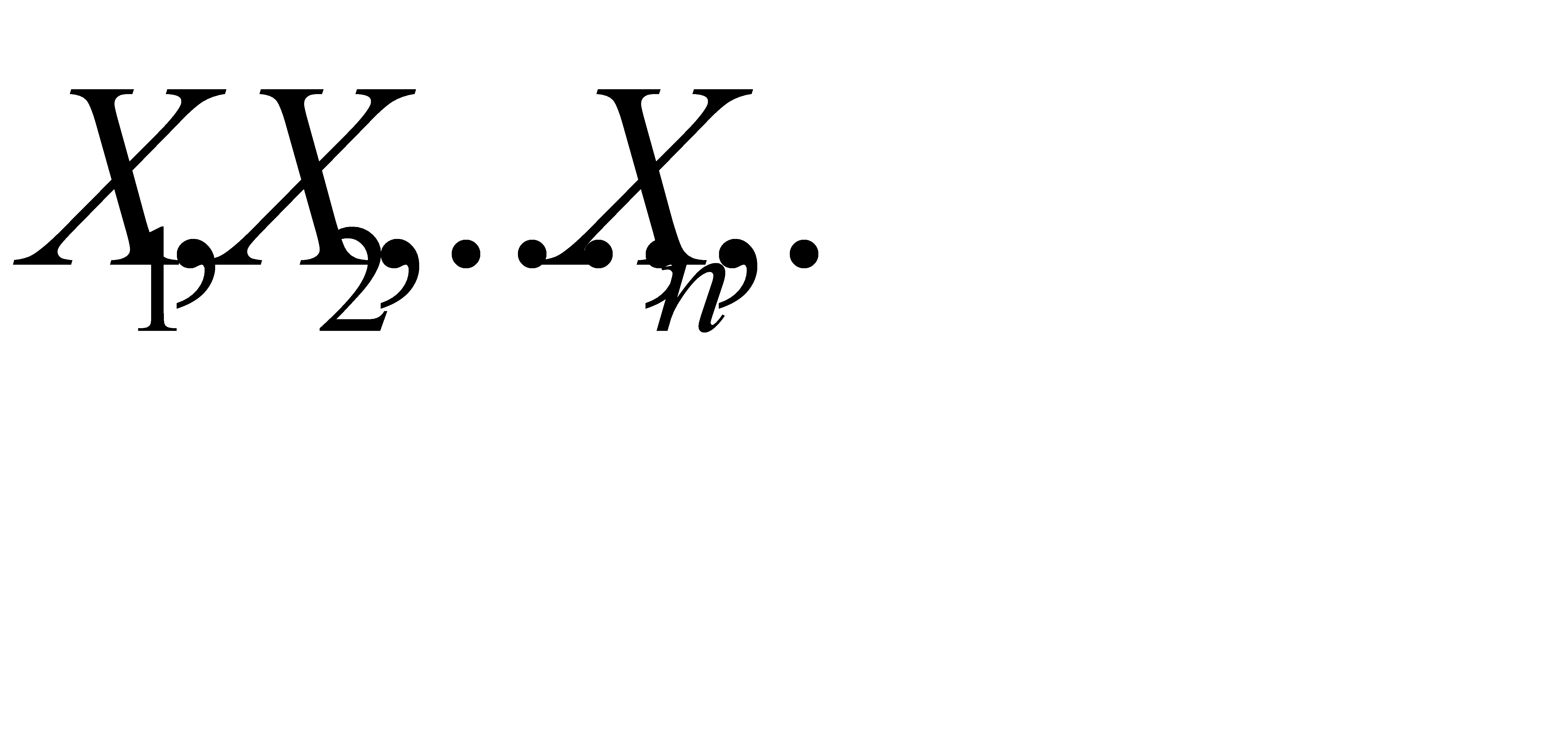 задана законом распределения
задана законом распределения
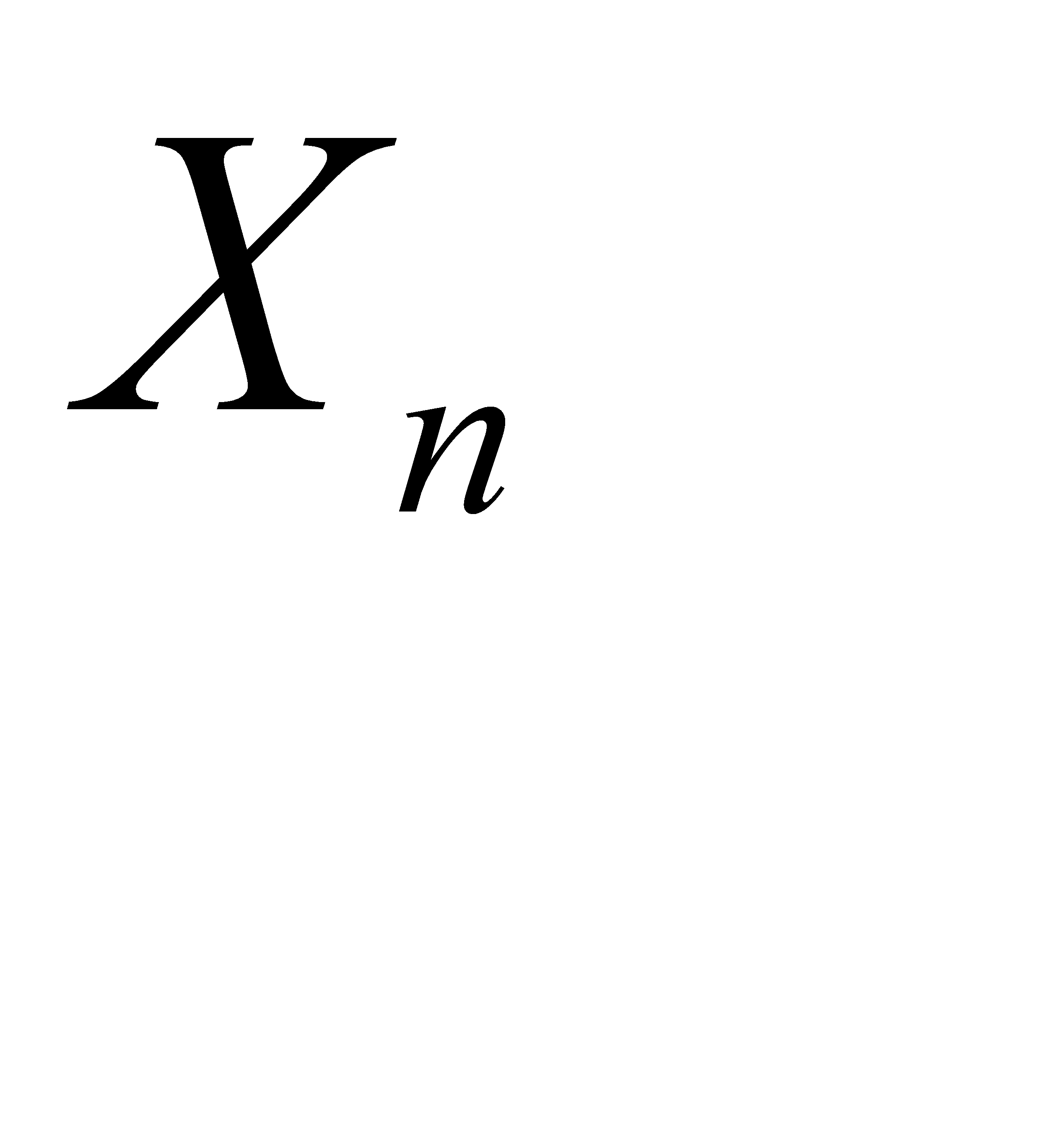
| a | -a |
| p | 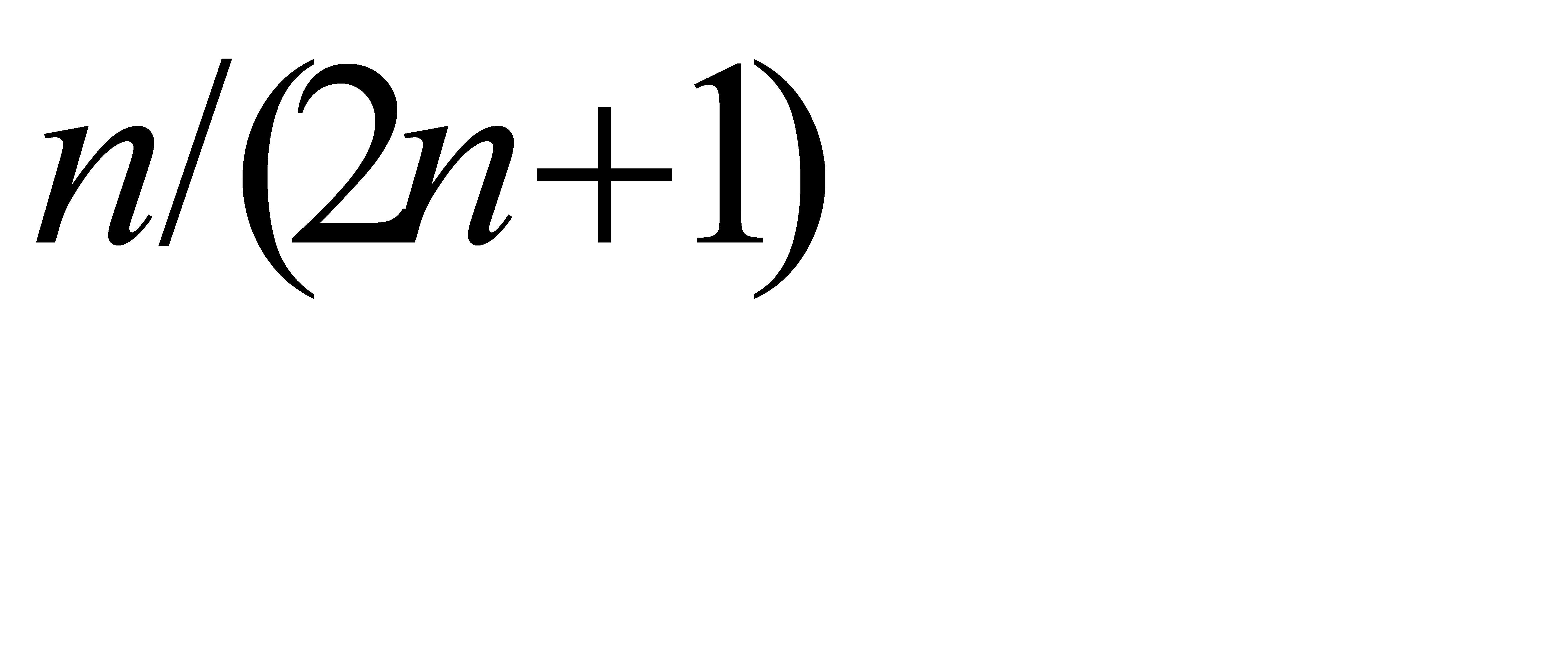
| 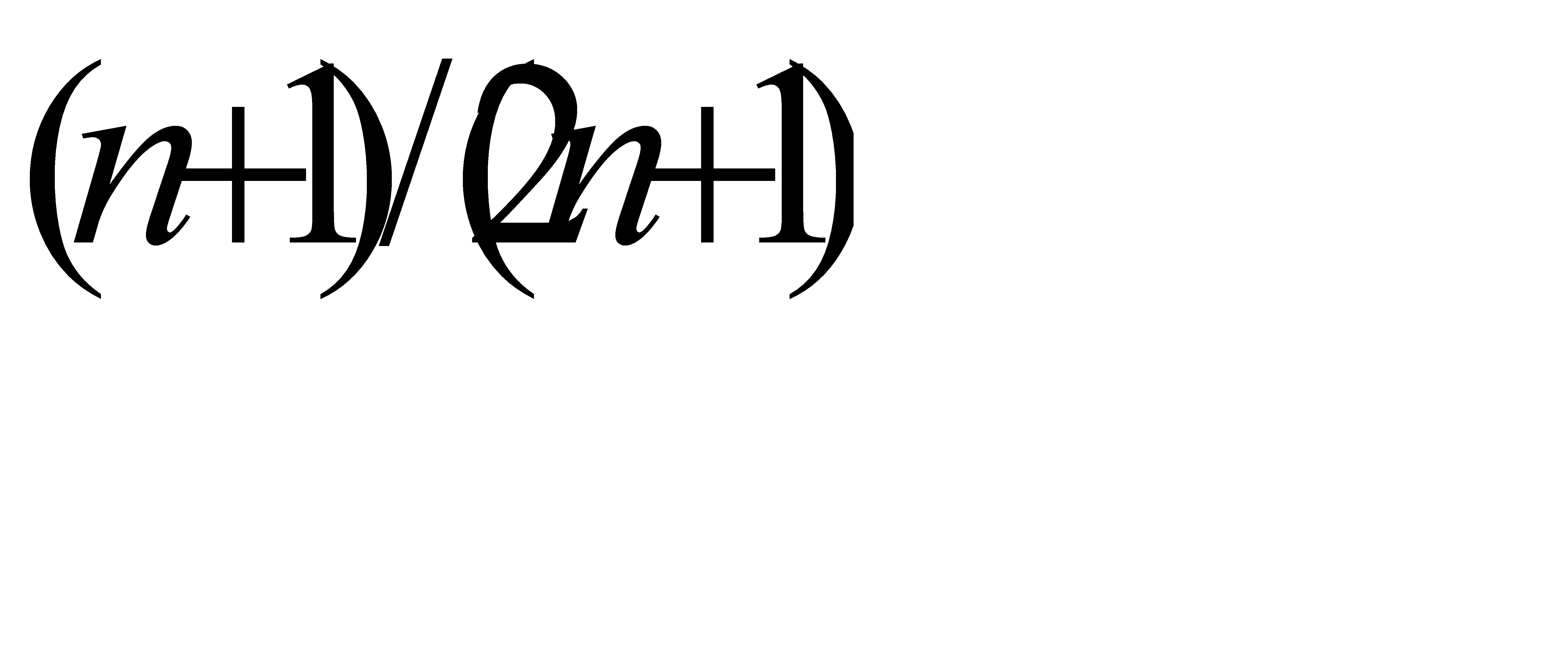
|
Применима ли к заданной последовательности теорема Чебышева?
Решение:
Для того, чтобы к последовательности случайных величин была применимы теорема Чебышева, достаточно, чтобы
1) эти величины были попарно независимы,
2) имели конечные математические ожидания,
3) имели равномерно ограниченные дисперсии.
Поскольку случайные величины независимы, то они подавно попарно независимы, т. е. первое требование теоремы Чебышева выполняется.
Проверим, выполняется ли требование конечности математических ожиданий:

Таким образом, каждая случайная величина имеет конечное (равное 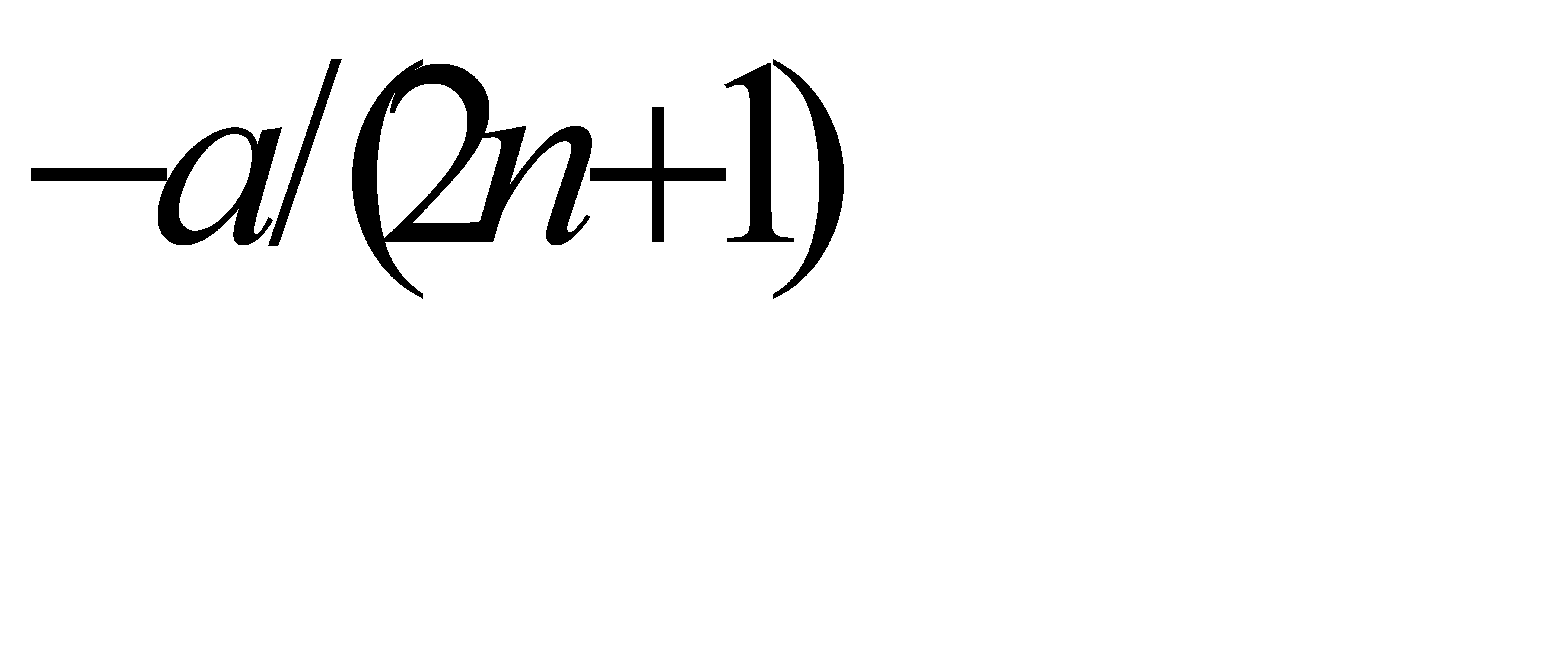 ) математическое ожидание, т. е. второе требование теоремы выполняется.
) математическое ожидание, т. е. второе требование теоремы выполняется.
Проверим, выполняется ли требование равномерной ограниченности дисперсии. Напишем закон распределения 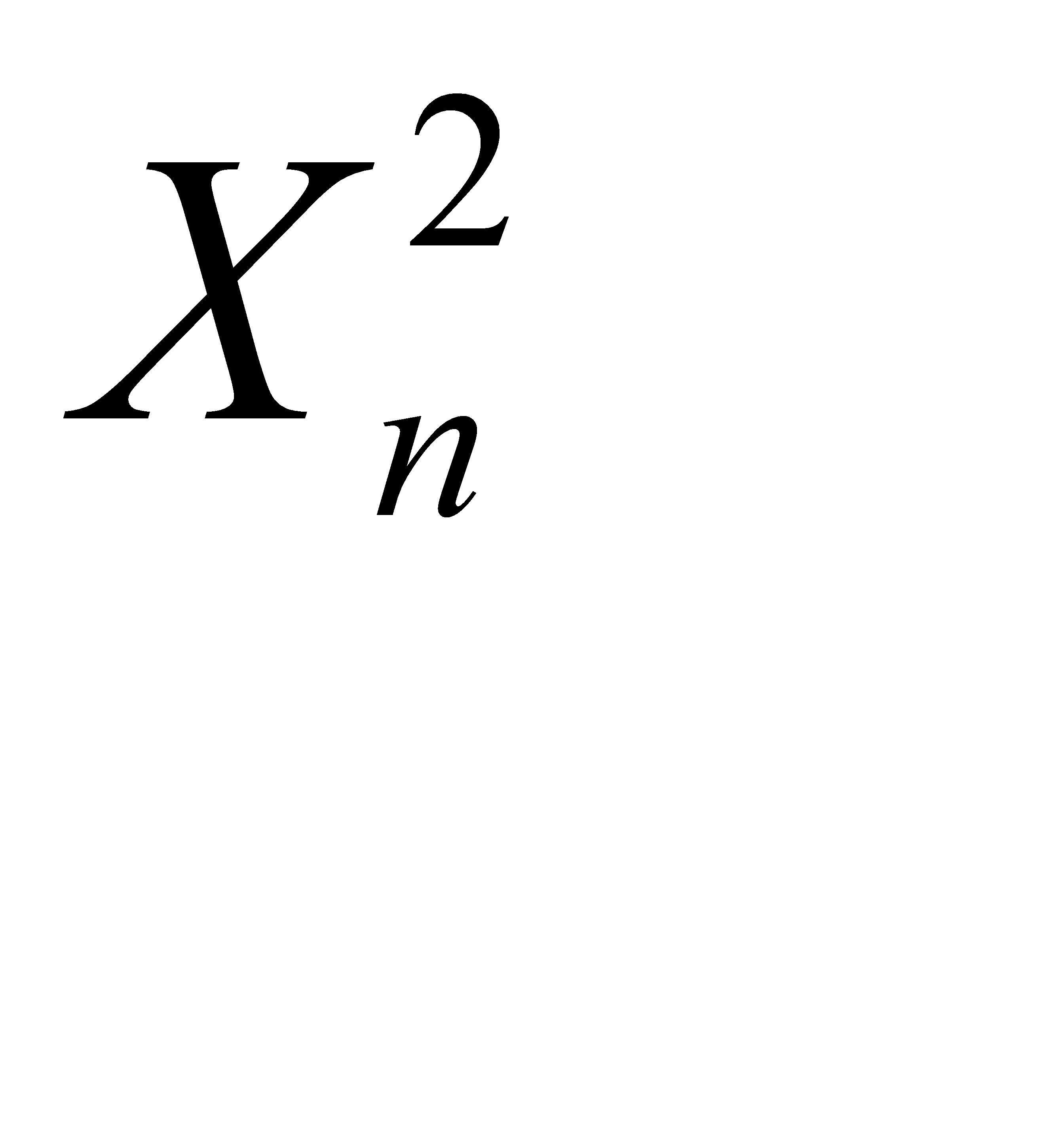 :
:
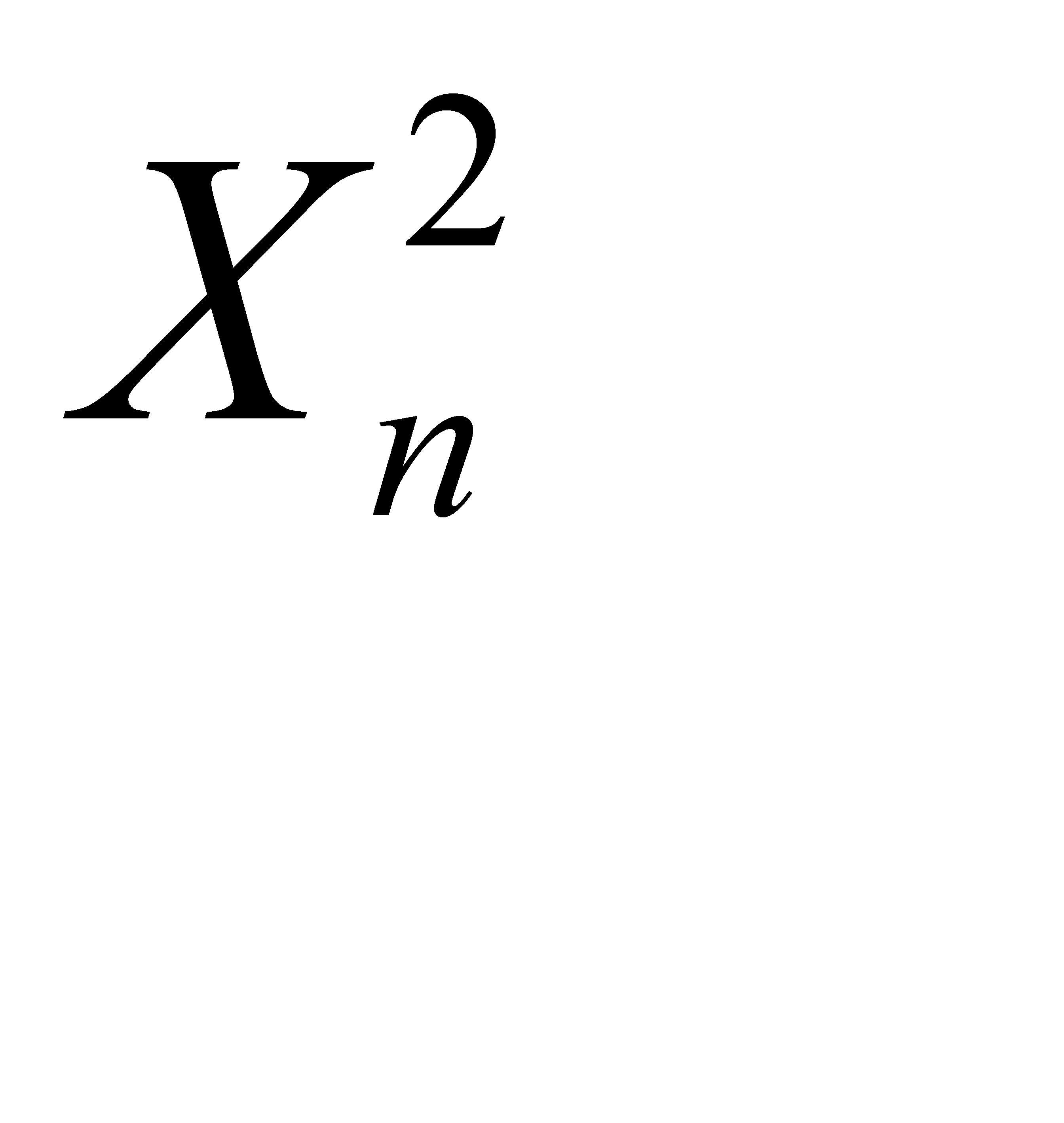
| a 2 | a 2 |
| p | 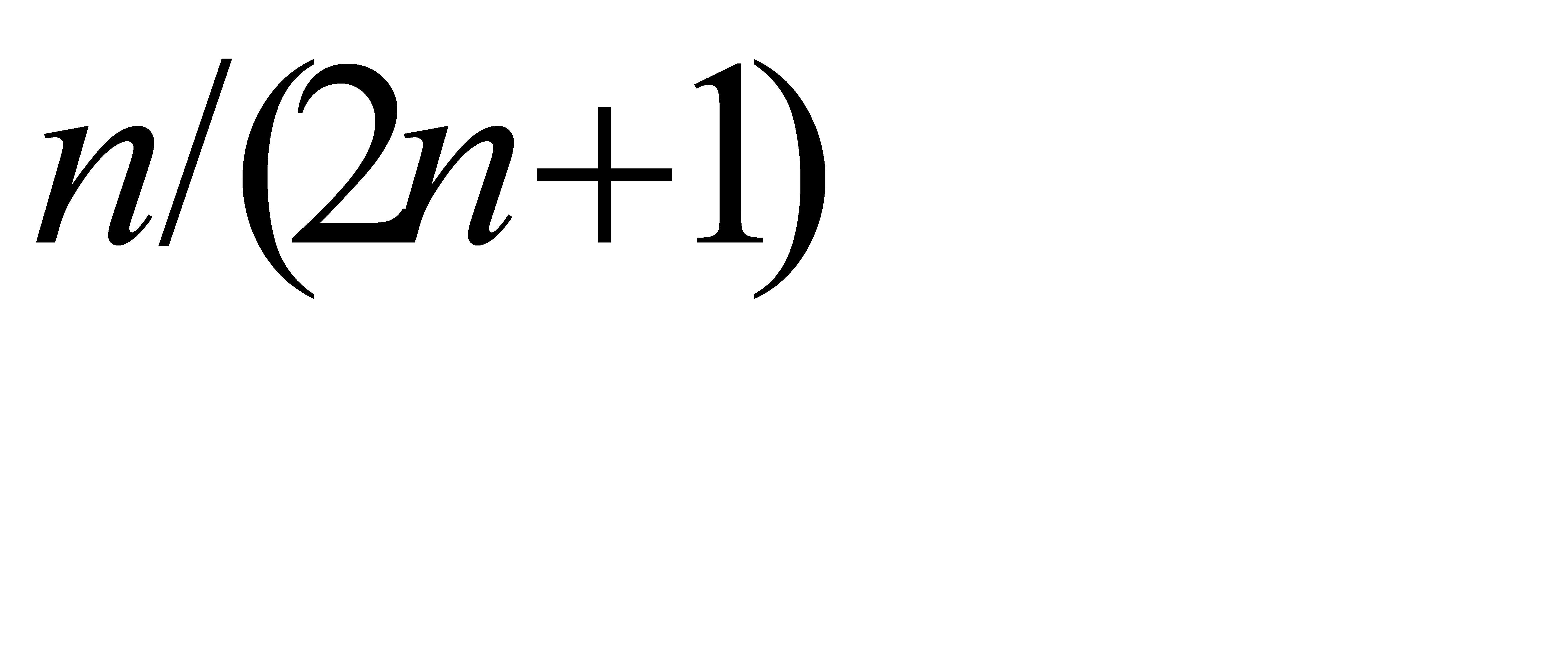
| 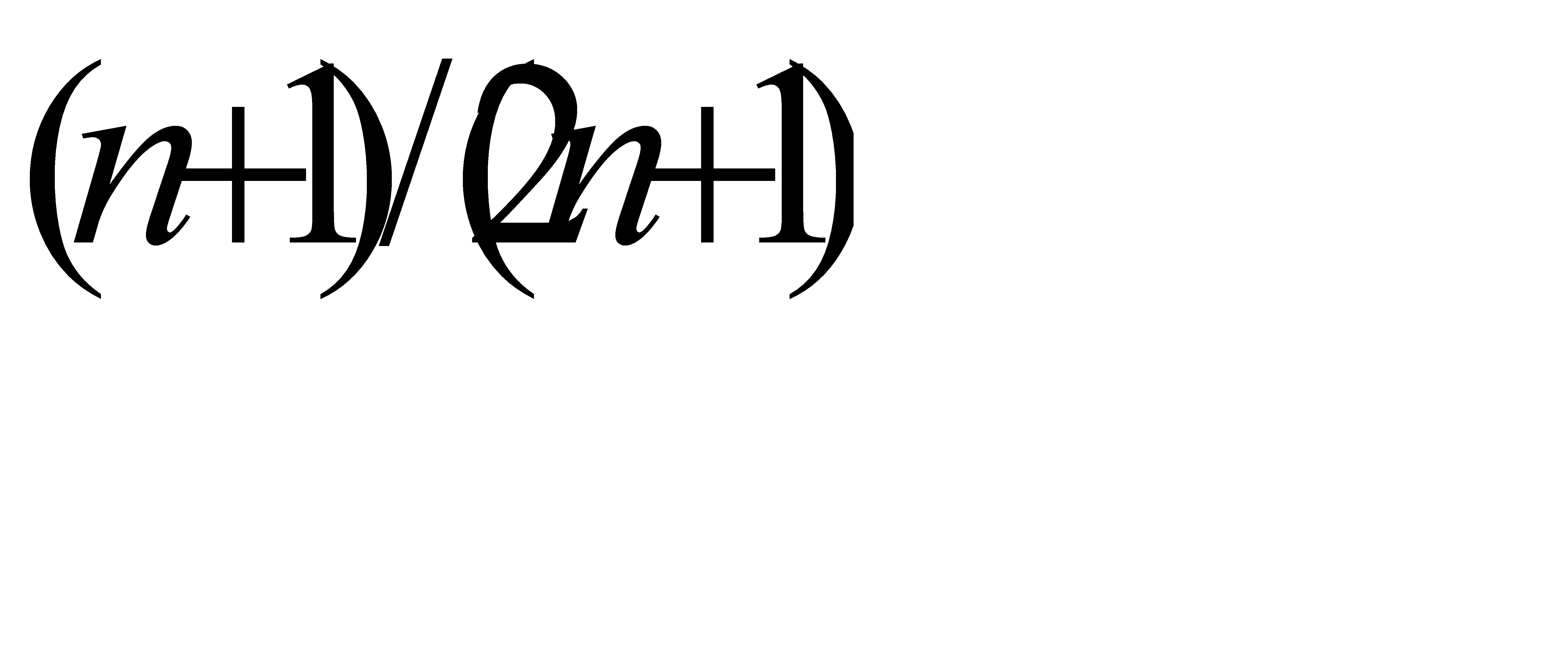
|
или, сложив вероятности одинаковых возможных значений,
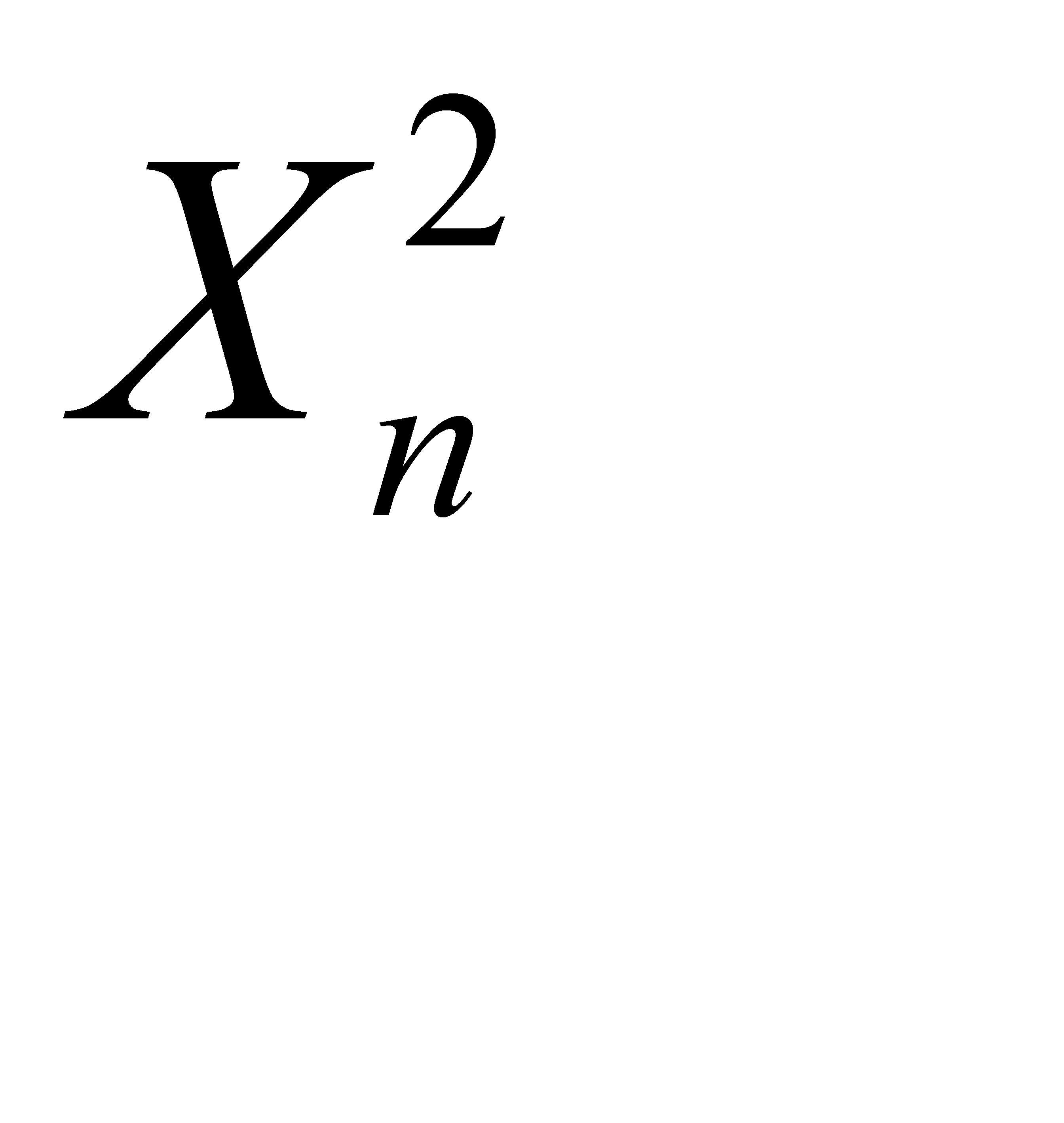
| a 2 |
| p |
Найдём математическое ожидание 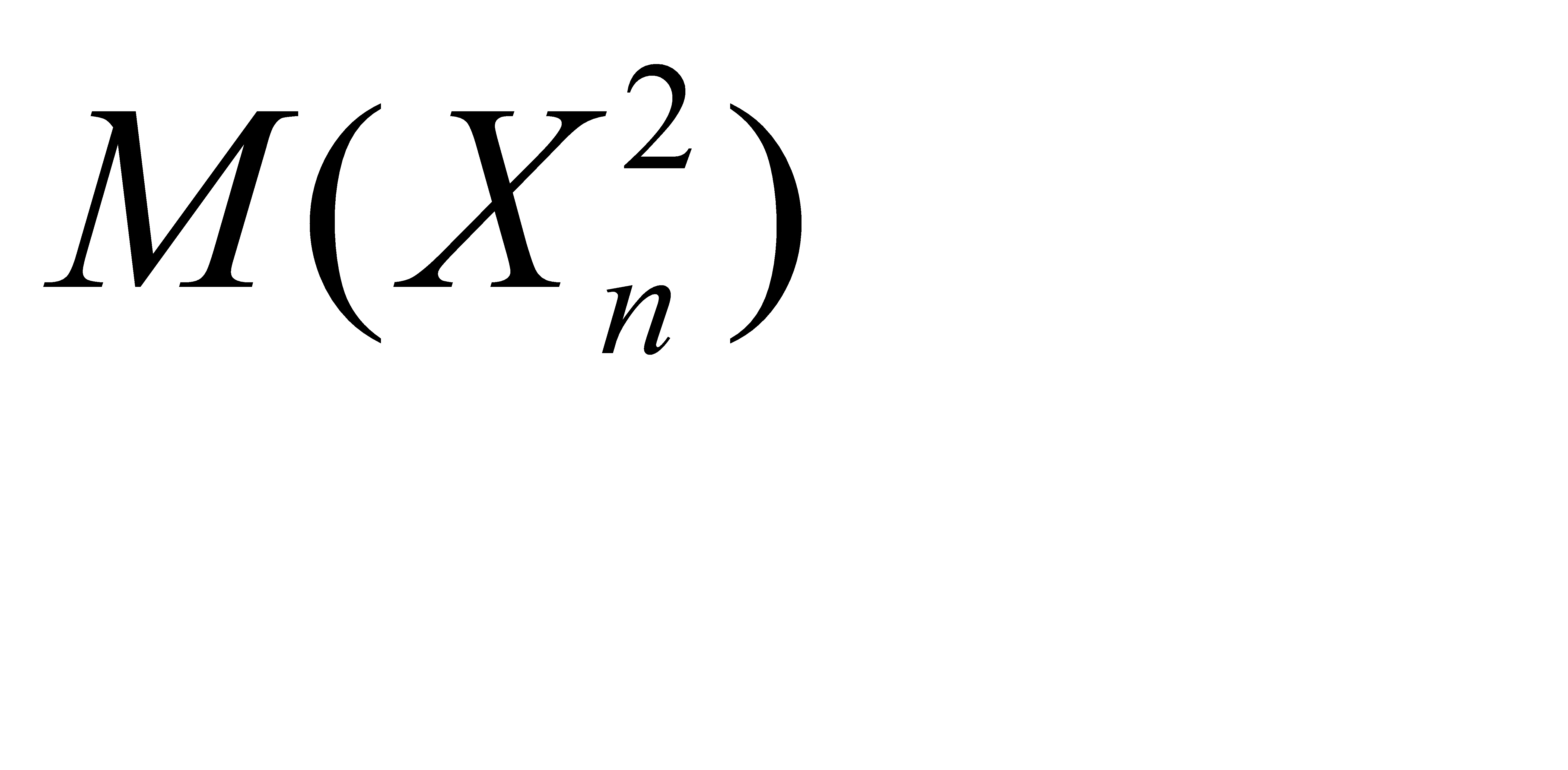 :
:
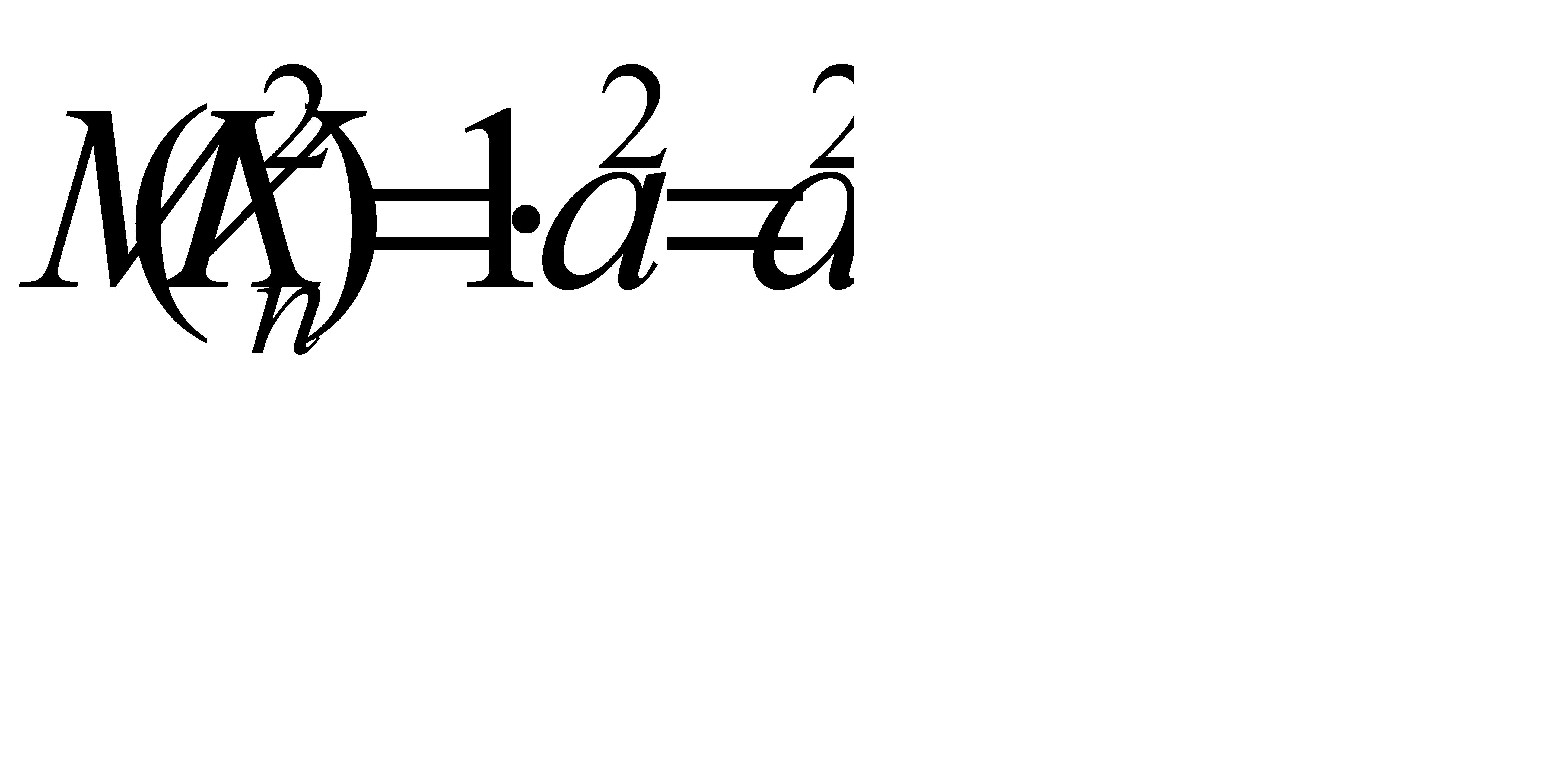
Найдём дисперсию 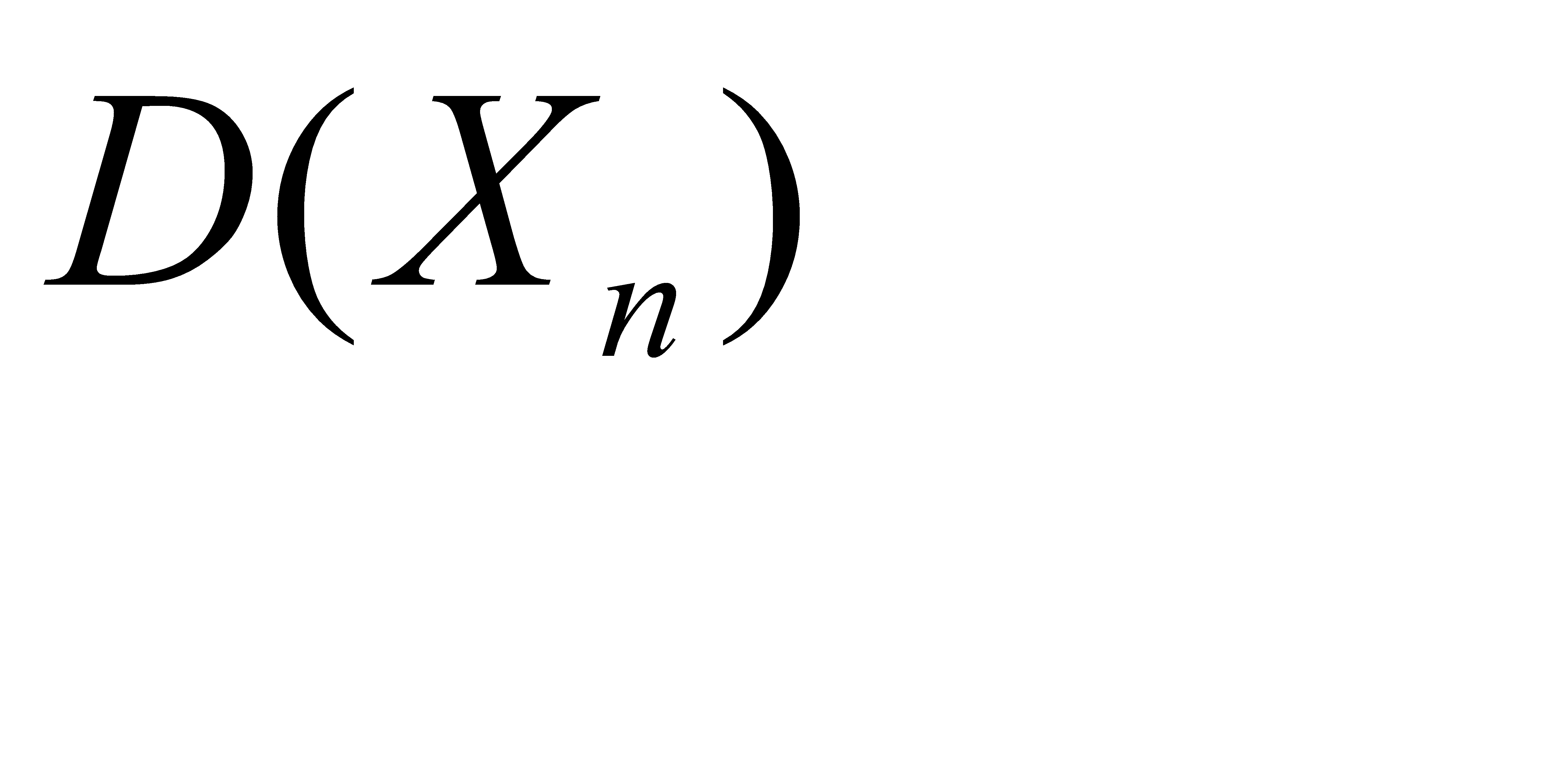 :
:

Эта функция возрастает, следовательно, чтобы вычислить константу, ограничивающую дисперсию, можно вычислить предел:
Таким образом, дисперсии заданных случайных величин равномерно ограничены
числом 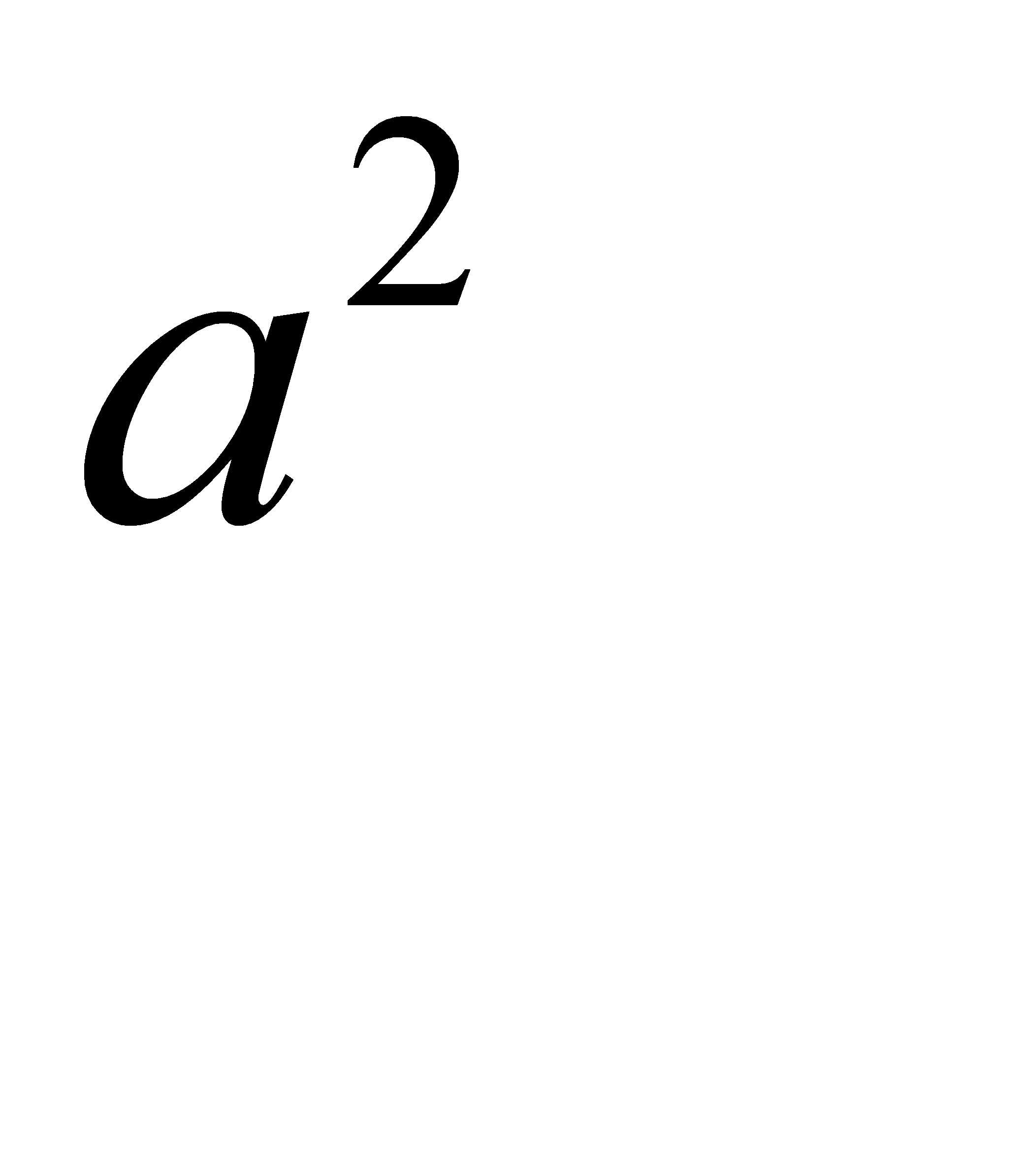 , т. е. третье требование выполняется.
, т. е. третье требование выполняется.
Итак, поскольку все требования выполняются, к рассматриваемой последовательности случайных величин теорема Чебышева применима.
Ответ: применима.
#249
Последовательность независимых случайных величин 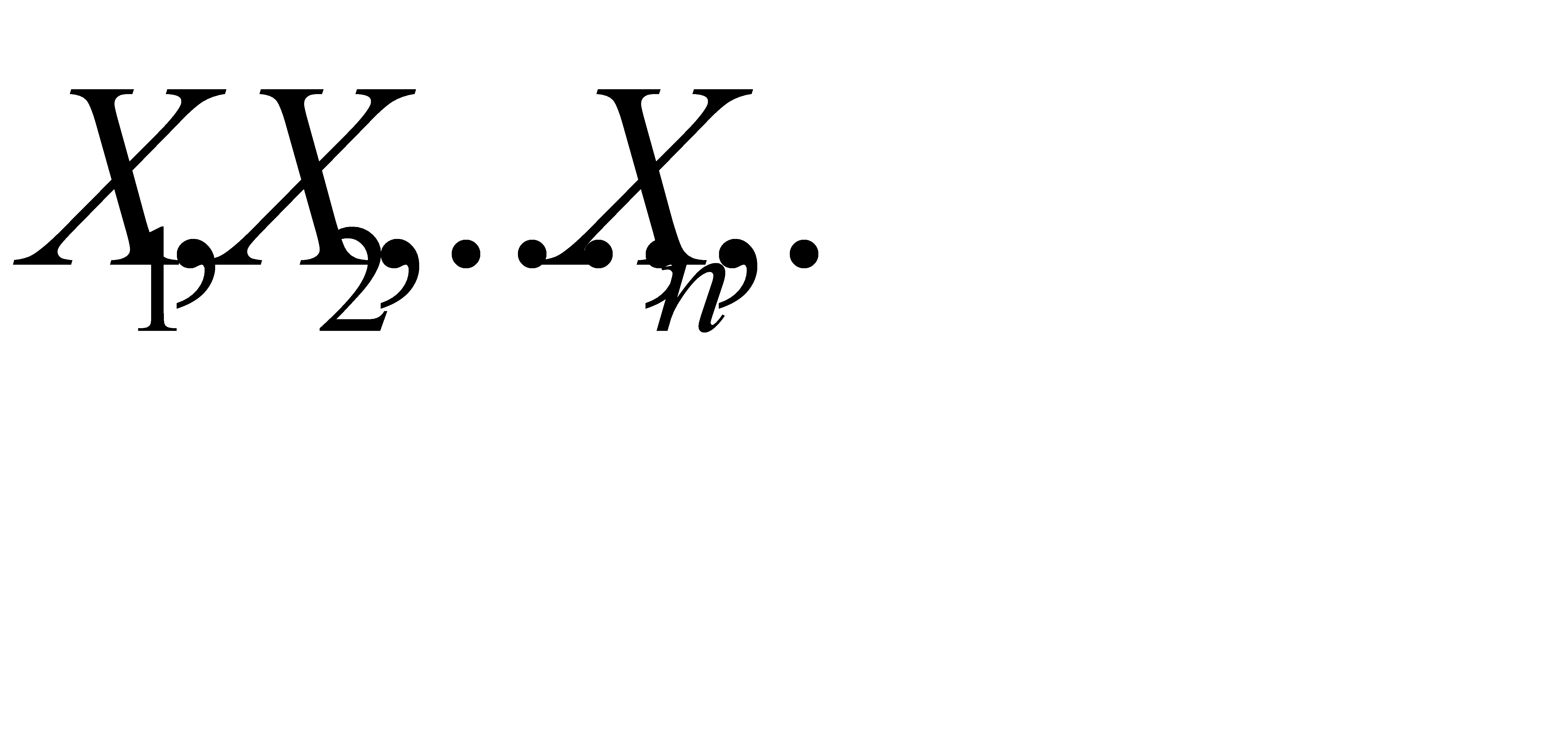 задана законом распределения
задана законом распределения
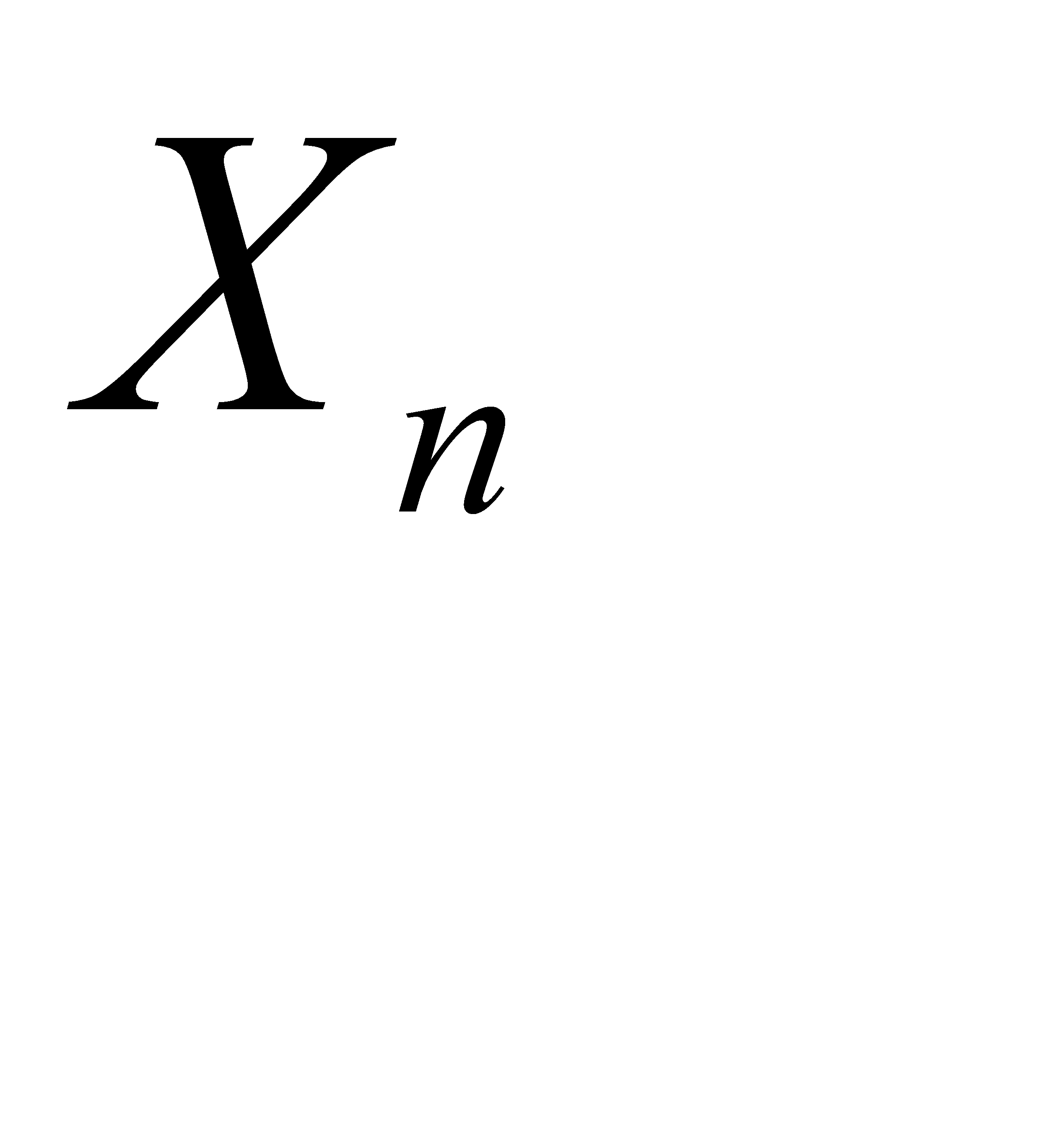
| n+1 | -n |
| p | 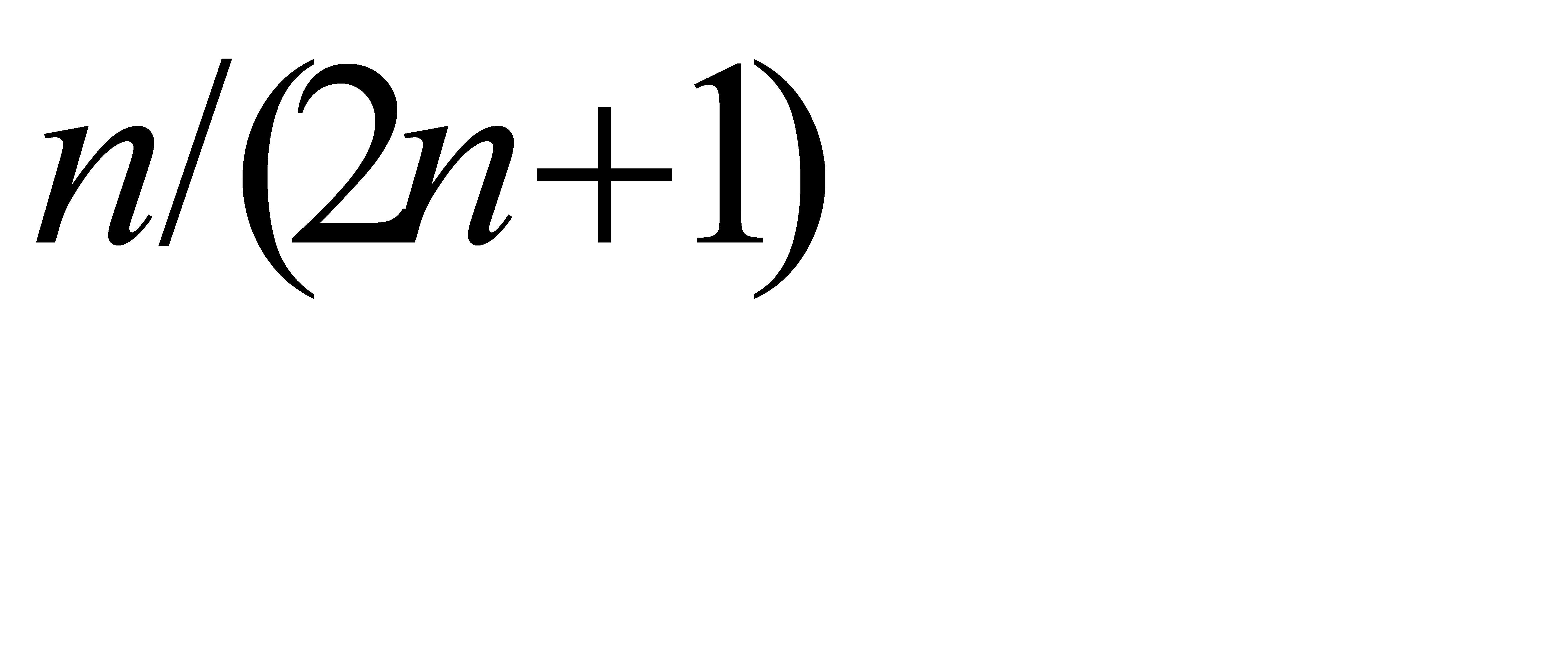
| 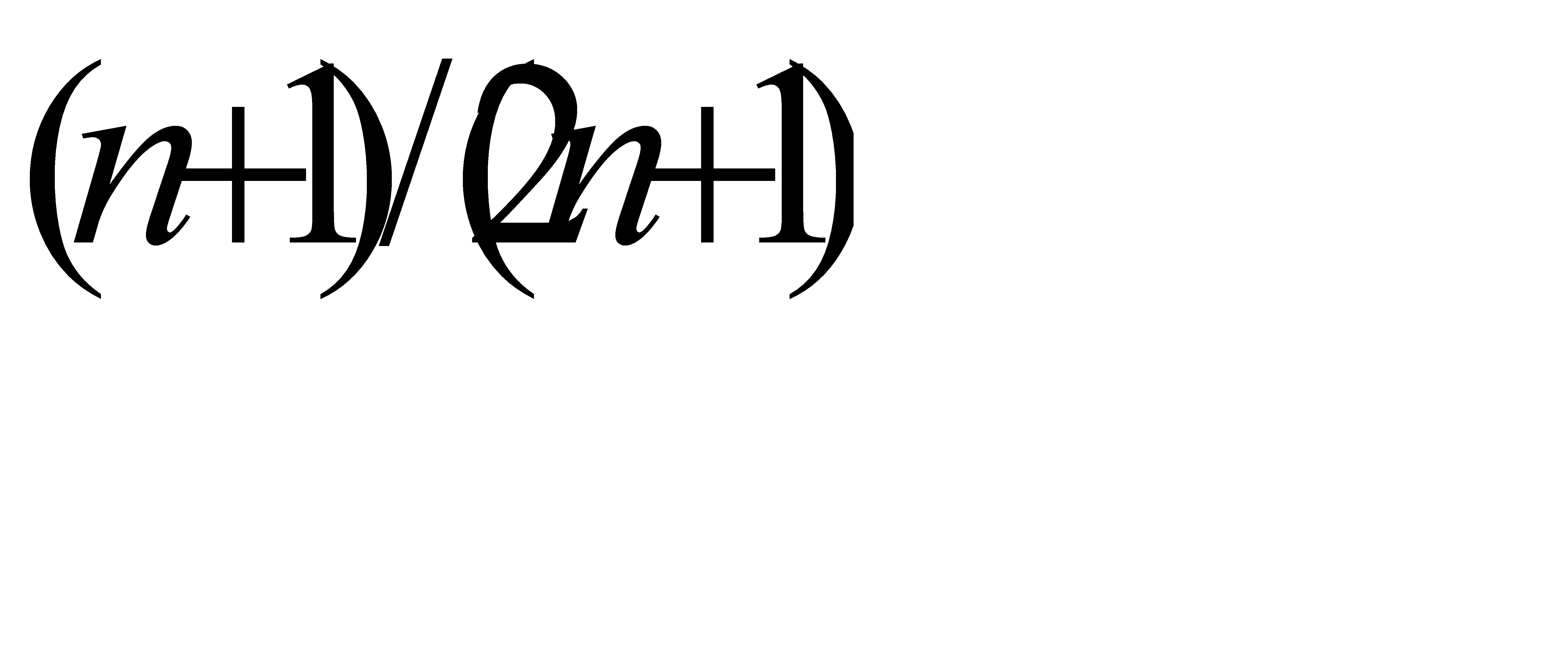
|
А) убедиться, что требование теоремы Чебышева о равномерной ограниченности дисперсии не выполняется
Б) можно ли отсюда заключить, что к рассматриваемой последовательности теорема Чебышева неприменима?
Решение:
А) Найдём математическое ожидание 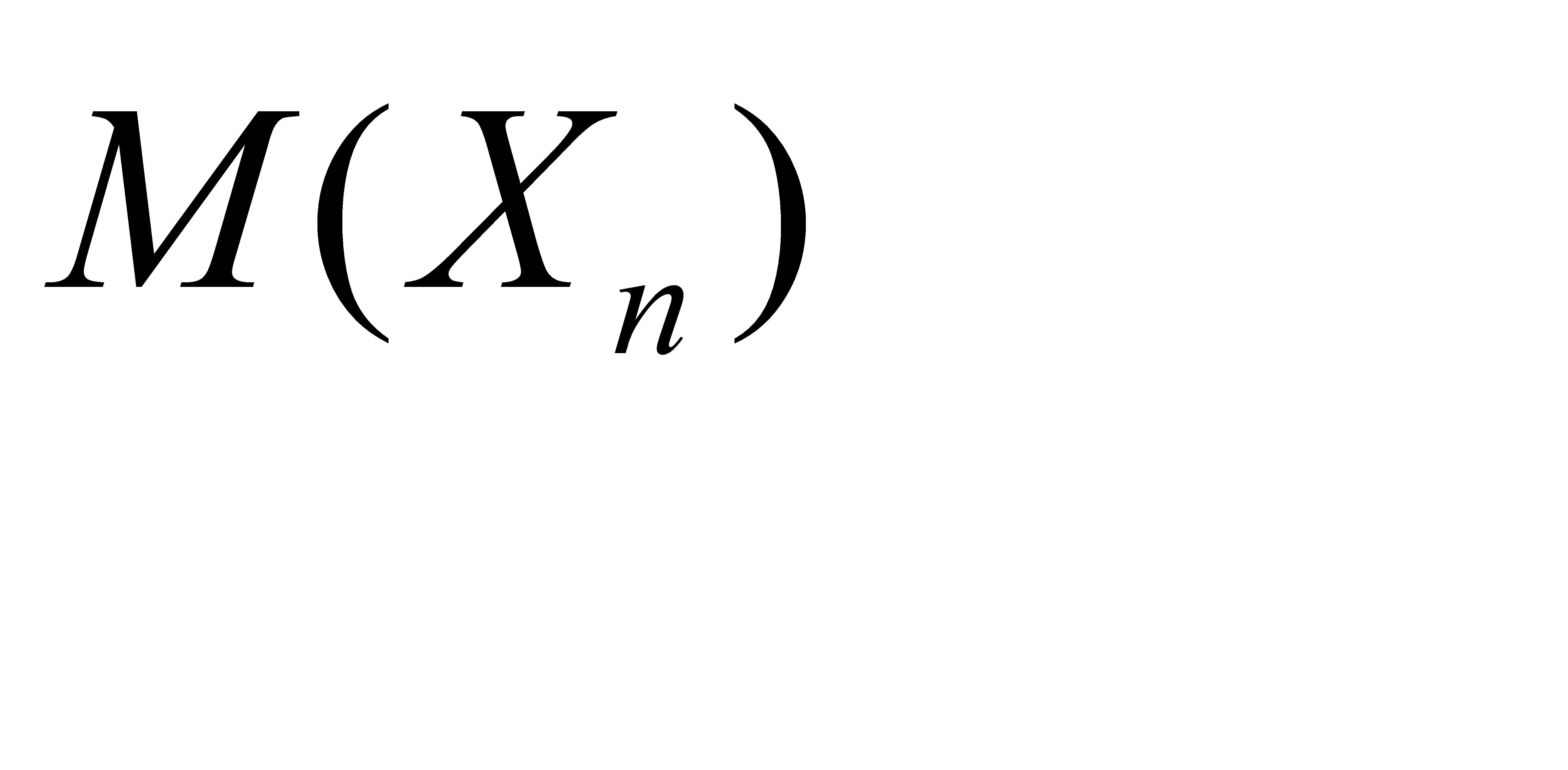 :
:

Проверим, выполняется ли требование равномерной ограниченности дисперсии. Напишем закон распределения 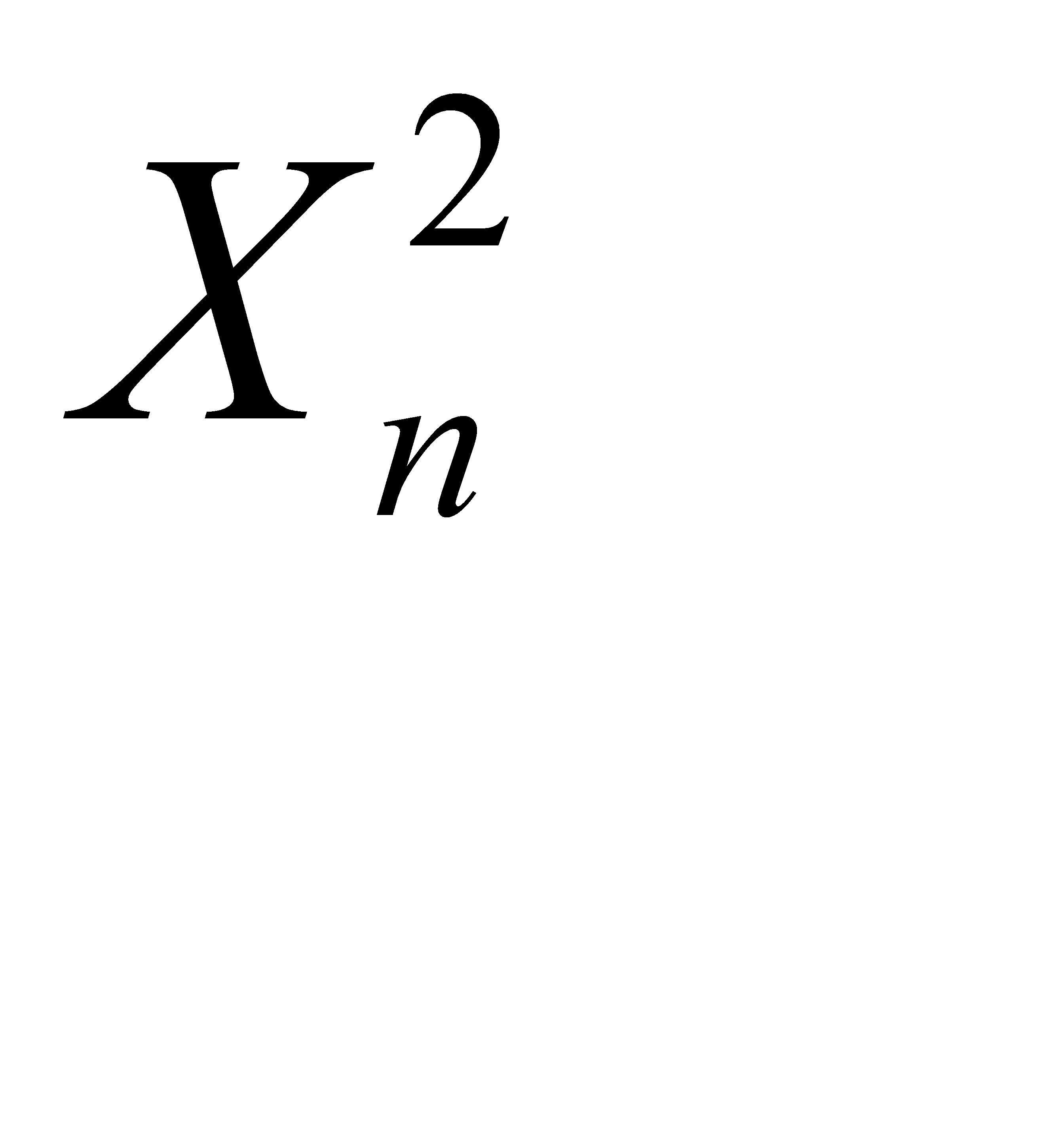 :
:
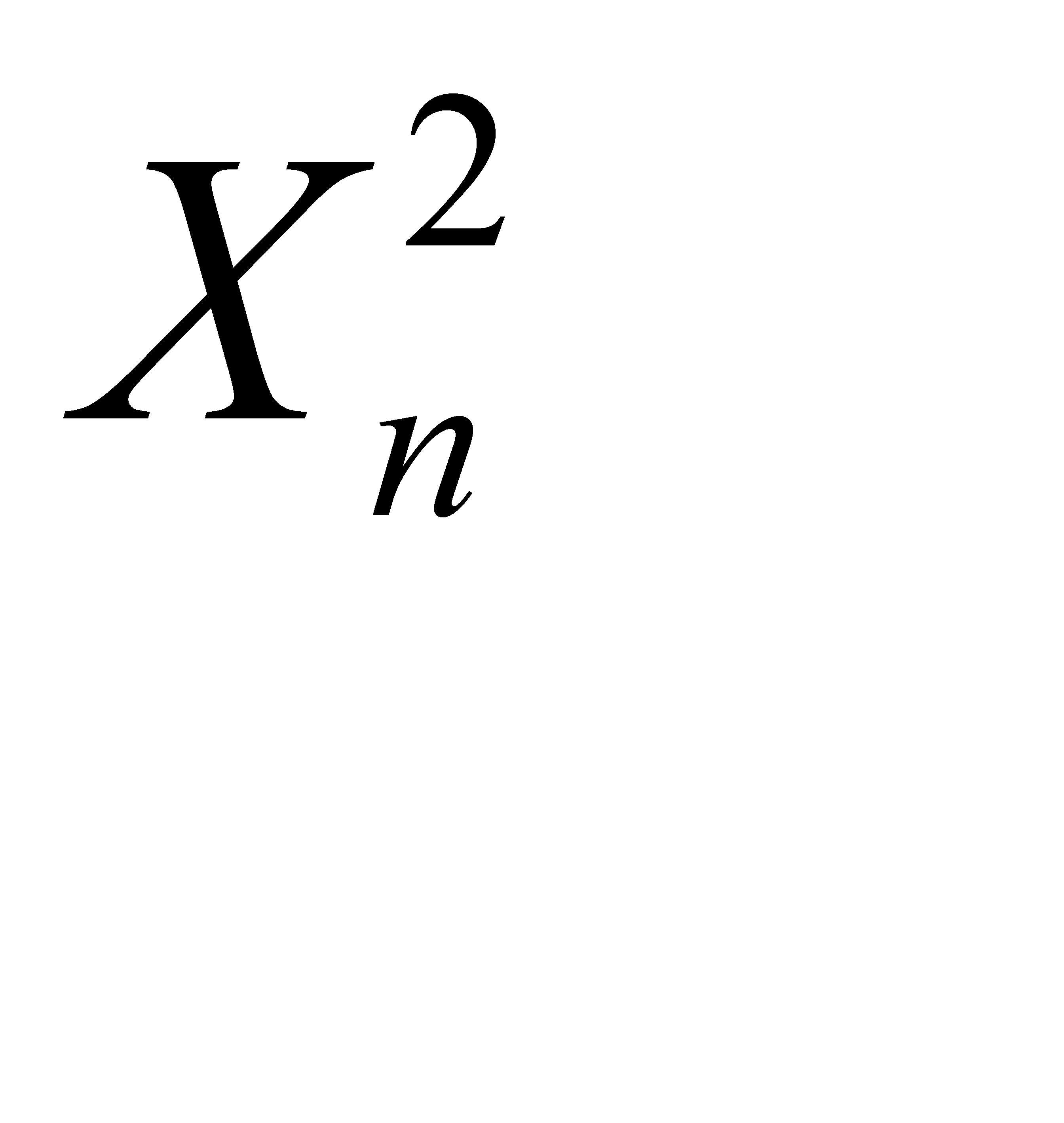
| 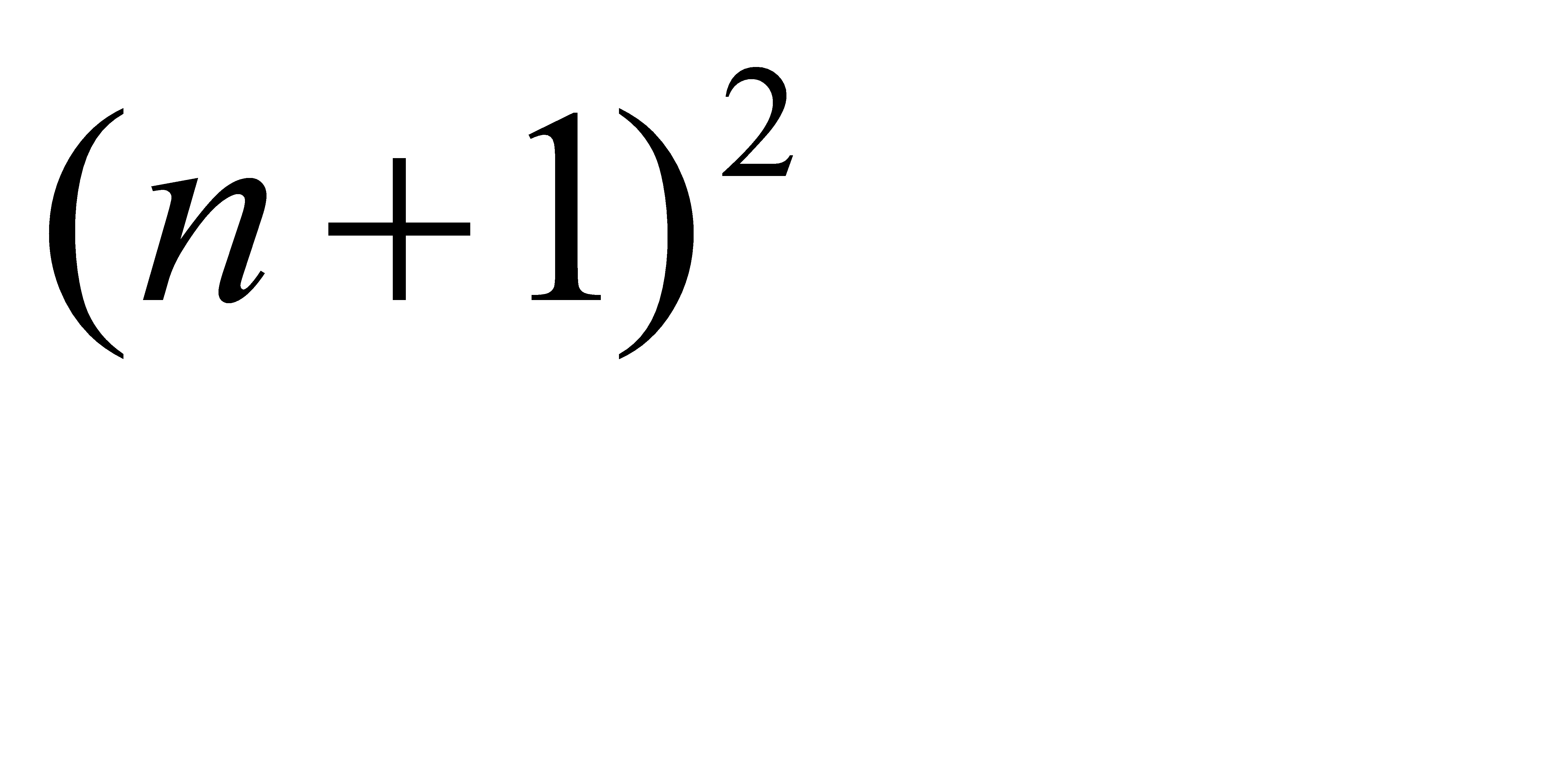
| 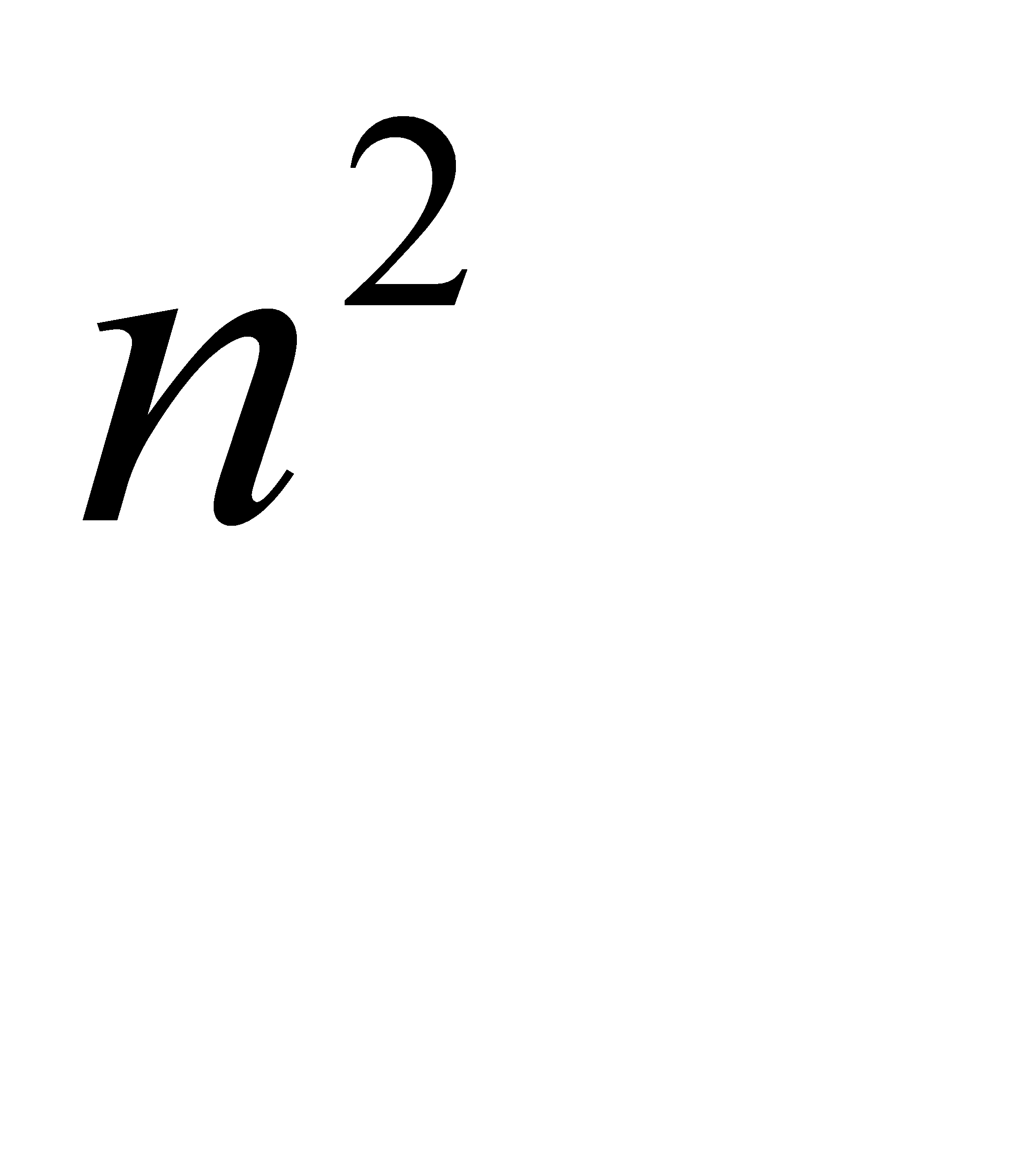
|
| p | 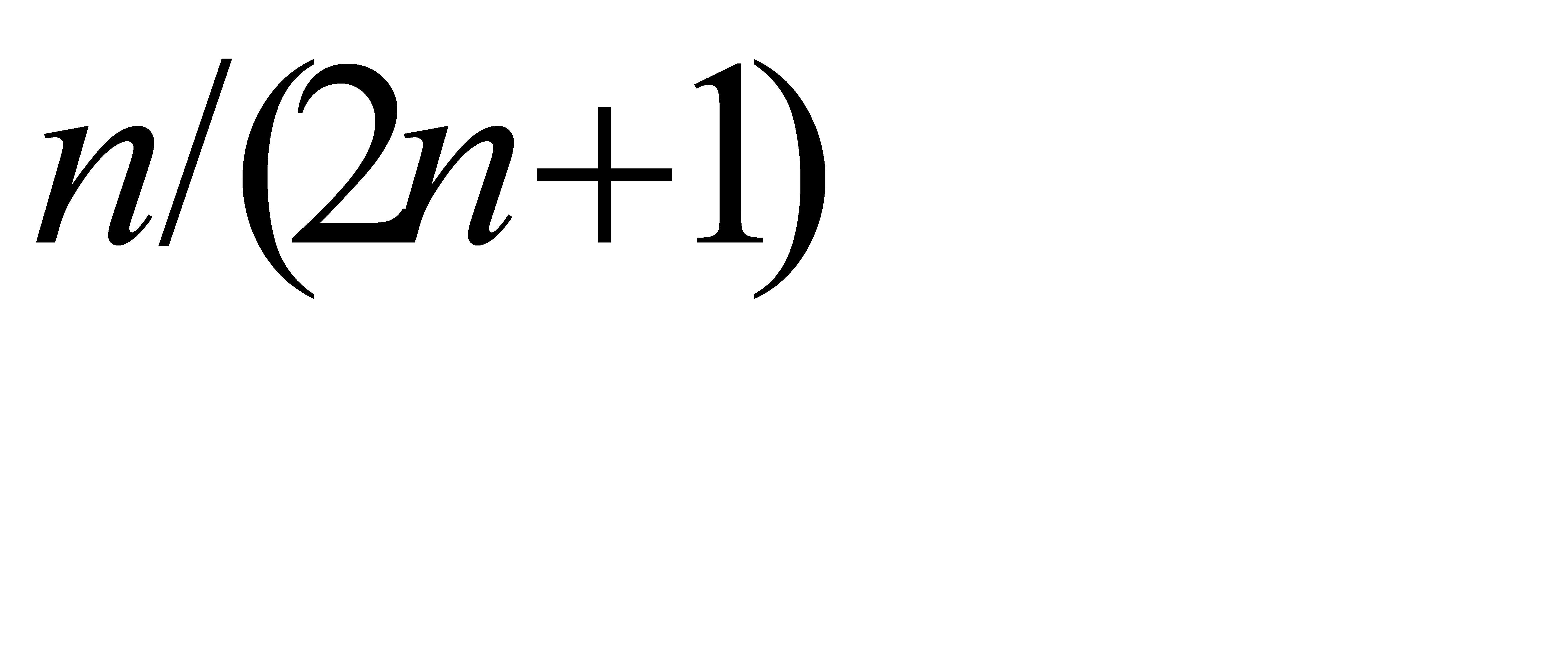
| 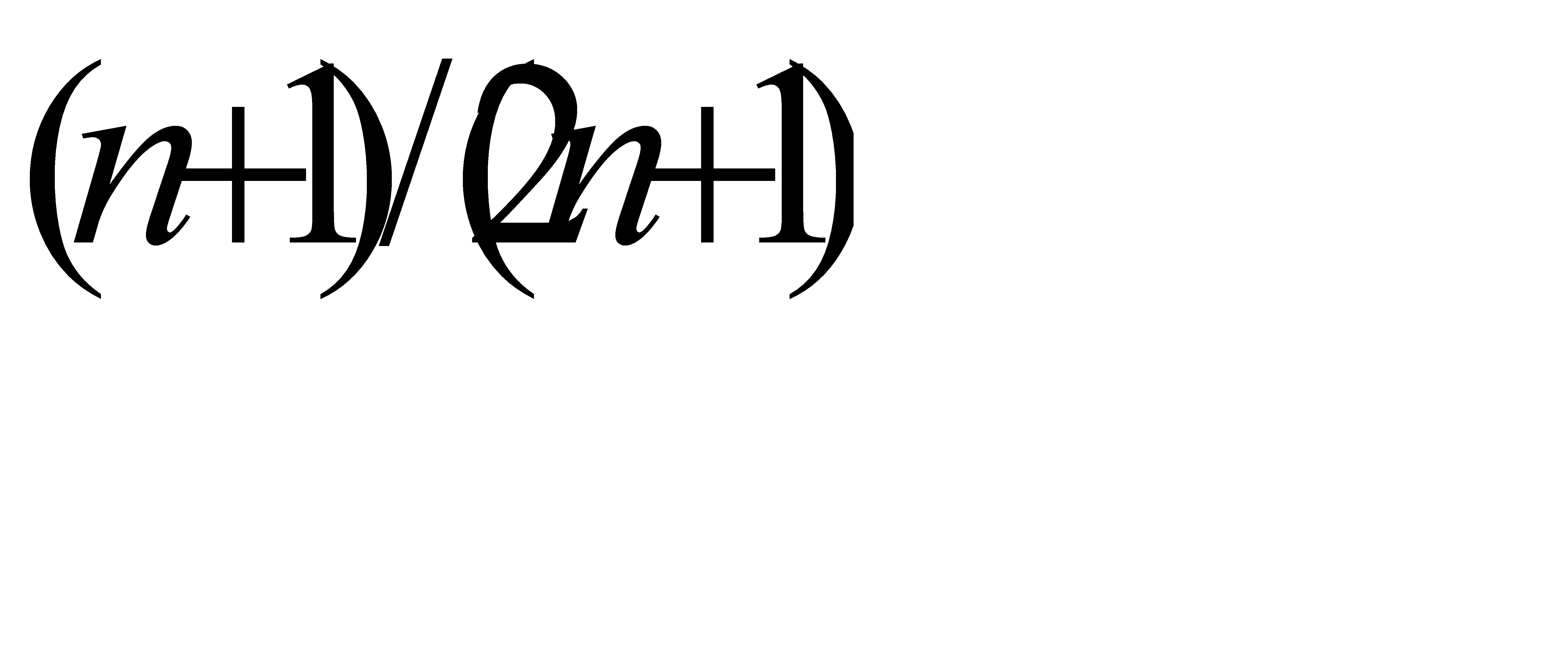
|
Найдём математическое ожидание 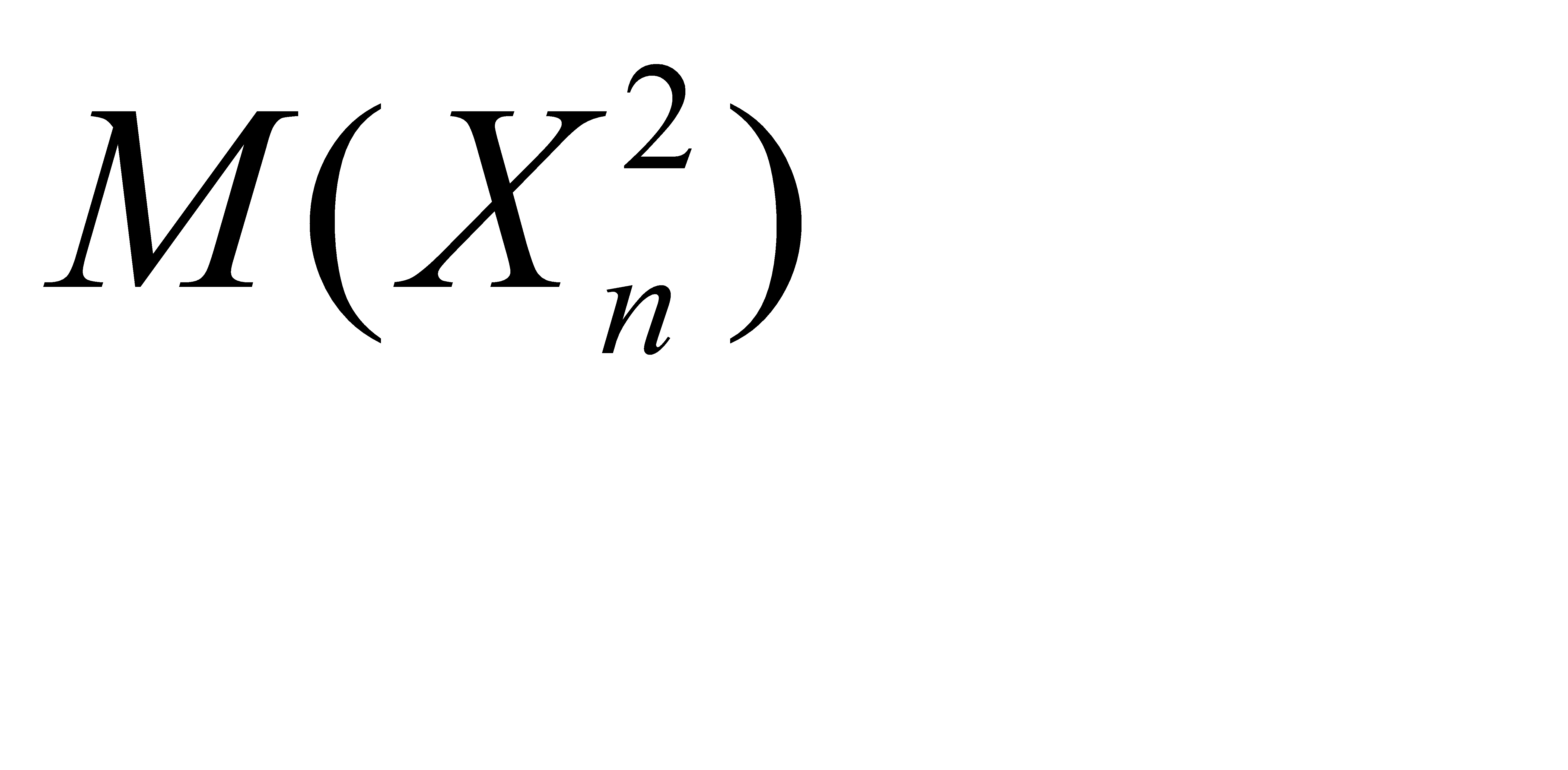 :
:

Найдём дисперсию 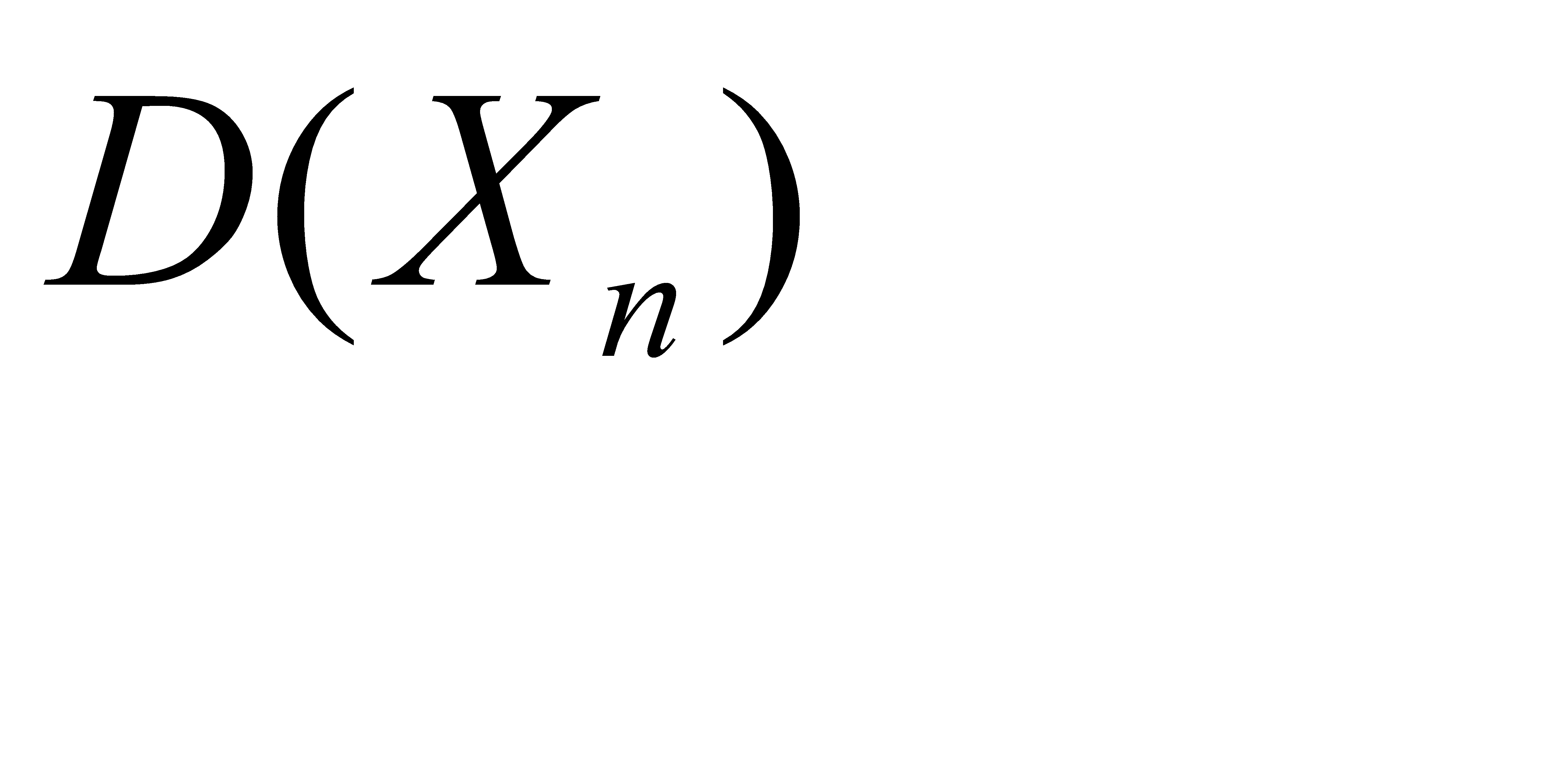 :
:
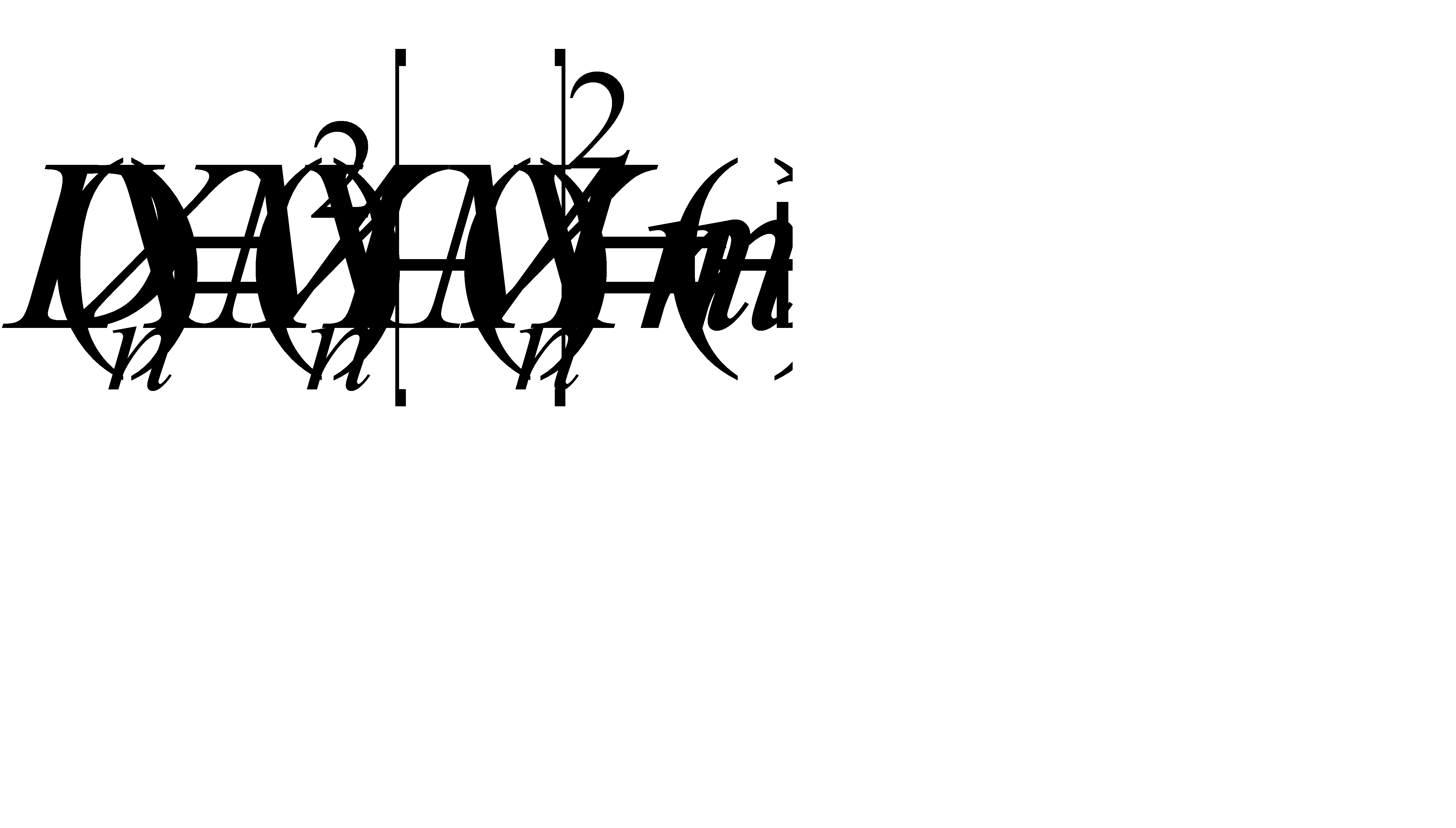
Эта функция возрастает, следовательно, чтобы вычислить константу, ограничивающую дисперсию, можно вычислить предел:
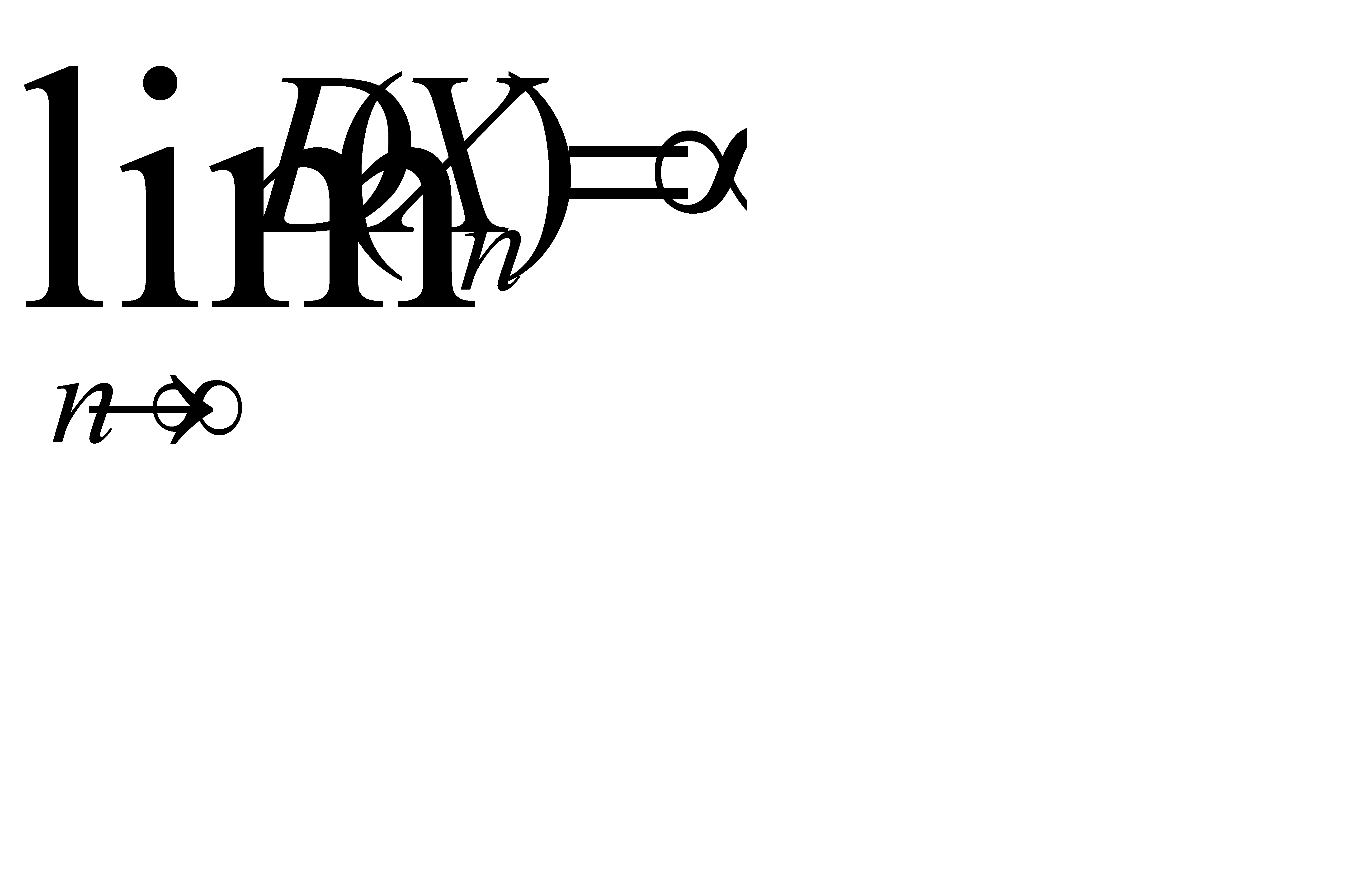
Таким образом, дисперсии заданных случайных величин неограниченны, что и требовалось доказать.
Б) Из формулировки теоремы Чебышева следует, что требование равномерной ограниченности дисперсий является достаточным, но не необходимым условием, поэтому нельзя утверждать, что к данной последовательности эту теорему применить нельзя.
#250
Задача:
Последовательность независимых случайных величин Х1, Х2, …, Хn, … задана законом распределения
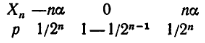
Применима ли к заданной последовательности теорема Чебышева?
Решение:
Поскольку случайные величины Хn независимы, то они подавно и попарно независимы, т. е. первое требование теоремы Чебышева выполняется.
Легко найти, что M(Xn)=0, т. е. первое требование конечности математических ожиданий выполняется.
Остается проверить выполнимость требования равномерной ограниченности дисперсий. По формуле
D(Xn)=M(Xn2)-[M(Xn)]2,
учитывай, что M(Xn)=0, найдем (выкладки предоставляются выполнить читателю)
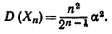
Временно предположим, что n изменяется непрерывно (чтобы подчеркнуть это допущение, обозначим n через х), и исследуем на экстремум функцию φ (х)=х2/2х-1.
Приравняв первую производную этой функции к нулю, найдем критические точки х1=0 и х2=ln 2.
Отбросим первую точку как не представляющую интереса (n не принимает значения, равного нулю); легко видеть, что в точек х2=2/ln 2 функция φ (х) имеет максимум. Учитывая, что 2/ln 2 ≈ 2. 9 и что N – целое положительное число, вычислим дисперсию D(Xn)= (n2/2n-1)α 2 для ближайших к числу 2. 9 (слева и справа) целых чисел, т. е. для n=2 и n=3.
При n=2 дисперсия D(X2)=2α 2, при n=3 дисперсия D(Х3)=9/4α 2. Очевидно,
(9/4)α 2> 2α 2.
Таким образом, наибольшая возможная дисперсия равна (9/4)α 2, т. е. дисперсии случайных величин Хn равномерно ограничены числом (9/4)α 2.
Итак, все требования теоремы Чебышева выполняются, следовательно, к рассматриваемой последовательности эта теорема применима.
#251
Задача:
Последовательность независимых случайных величин X1, X2, …, Xn, … задана законом распределения
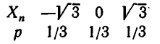
Применима ли к заданной последовательности теорема Чебышева?
Замечание. Поскольку случайные величины Х, одинаково распределены и независимы, то читатель, знакомый с теоремой Хинчина, может ограничиться вычислением лишь математического ожидания и убедиться, что оно кончено.
Решение:
Поскольку случайные величины Хn независимы, то они подавно и попарно независимы, т. е. первое требование теоремы Чебышева выполняется.
Легко найти, что M(Xn)=0, т. е. первое требование конечности математических ожиданий выполняется.
Остается проверить выполнимость требования равномерной ограниченности дисперсий. По формуле
D(Xn)=M(Xn2)-[M(Xn)]2,
учитывай, что M(Xn)=0, найдем
D(Xn)=2
Таким образом, наибольшая возможная дисперсия равна 2, т. е. дисперсии случайных величин Хn равномерно ограничены числом 2.
Итак, все требования теоремы Чебышева выполняются, следовательно, к рассматриваемой последовательности эта теорема применима.
#252
Задача:
Случайная величина Х задана функцией распределения
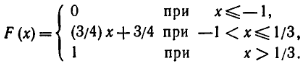
Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0, 1/3).
Решение:
Вероятность того, что Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: P(a< X< b)=F(b)-F(a). Положив а=0, b=1/3, получим
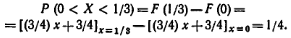
#253
Задача:
Случайная величина Х задана на всей оси Ох функцией распределена F(x)=1/2+(arctgx)/π. Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0, 1).
Решение:
Вероятность того, что Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: P(a< X< b)=F(b)-F(a). Положив а=0, b=1, получим
Р(0< Х < 1) = F(1)-F(0) = [1/2+1/4]x=1 - [1/2+0]x=0 = 1/4
#254
Задача:
Случайная величина Х функцией распределения
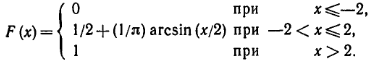
Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (-1, 1).
Решение:
Вероятность того, что Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: P(a< X< b)=F(b)-F(a). Положив а=-1, b=1, получим
Р(-1< Х < 1) = F(1)-F(-1) = [1/2+5/6]x=-1 – [1/2+1/6]x=1 = 1/3.
#255
Задача:
Функция распределения непрерывной случайной величины Х (времени безотказной работы некоторого устройства) равна F(х)=1-е-х/T(х≥ 0). Найти вероятность безотказной работы устройства за время х≥ Т.
Решение:
Вероятность того, что Х примет значение, заключенное в интервале x≥ T, равна приращению функции распределения на этом интервале: P(0< X< T)=F(T)-F(0). Положив это, получим
P(x≥ T) = 1 - P(T< x) = 1 - P(0< X< T) = 1 – F(T)+F(0) = 1 - (1-1/e)+(1-1) = 1/e
#256
Задача:
Случайная величина Х задана функцией распределения
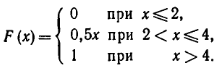
Найти вероятность того, что в результате испытания Х примет значение: а) меньшее 0. 2; б) меньшее трех; в) не меньшее трех; г) не меньшее пяти.
Решение:
а) Так как при х≤ 2 функция F(х)=0, то F(0, 2)=0, т. е. P(х < 0, 2)=0;
б) Р(Х < 3) = F(3) = [0. 5x-1]x=3 = 1. 5-1 = 0. 5;
в) события Х≥ 3 и Х< 3 противоположны, поэтому Р(Х≥ 3)+Р(Х< 3)=1. Отсюда, учитывая, что Р(Х< 3)=0. 5 [см. п. б. ], получим Р(Х≥ 3) = 1-0. 5 = 0. 5;
г) сумма вероятностей противоположных событий равна единице, поэтому Р(Х≥ 5)+Р(Х< 5)=1. Отсюда, используя условие, в силу которого при х> 4 функция F(x)=1, получим Р(Х≥ 5) = 1-Р(Х< 5) = 1-F(5) = 1-1 = 0.
#257
Задача:
Случайная величина Х задана функцией распределния
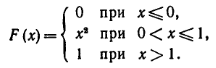
Найти вероятность того, что в результате четырех независимых испытаний величина Х ровно три раза примет значение, принадлежащее интервалу (0. 25, 0. 75).
Решение:
Вероятность того, что Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: P(a< X< b)=F(b)-F(a). Положив а=0. 25, b=0. 75, получим
P(0. 25< X< 0. 75) = F(0. 75)-F(0. 25) = 0. 5
#258
Случайная величина X задана на всей оси Ox функцией распределения . Найти возможное значения
, удовлетворяющее условию: с вероятностью
случайная X в результате испытания примет значение большее
Решение. События и
- противоложные, поэтому
. Следовательно,
. Так как
, то
.
По определению функции распределения, .
Следовательно, , или
Отсюда
, или
.
#259
Случайная величина X задана на всей оси Ox функцией распределения . Найти возможное значения
, удовлетворяющее условию: с вероятностью
случайная X в результате испытания примет значение большее
Решение. События и
- противоложные, поэтому
. Следовательно,
. Так как
, то
.
По определению функции распределения, .
Следовательно, , или
. Отсюда
, или
.
#260
Дискретная случайная величина X задана законом распределения
Найти функцию распределения и начертить ее график.
Решение.
2. Если , то
. Действительно, значений меньших 2 величина X не принимает. Следовательно, при
функция
.
3. Если , то
. Действительно, X может принимать значение 2 с вероятностью 0, 5.
4. 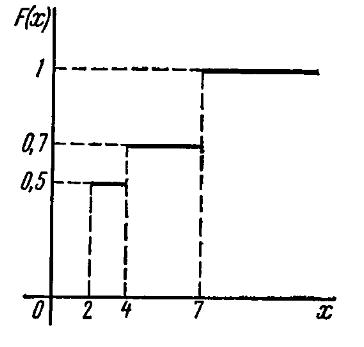 Если
Если , то
. Действительно, X может принять значение 2 с вероятностью 0, 5 и значение 4 с вероятностью 0, 2; следовательно, одно из этих значений, безразлично какое, X может принять (по теореме о сложении вероятностей несовместных событий) с вероятностью
.
5. Если , то
. Действительно, событие
достоверно и вероятность его равна единице.
Итак, искомая функция распределения имеет вид
#261
Дискретная случайная величина X задана законом распределения
Найти функцию распределения и начертить ее график.
Решение.
1. Если , то
. Действительно, значений меньших 3 величина X не принимает. Следовательно, при
функция
.
2. Если , то
. Действительно, X может принимать значение 3 с вероятностью 0, 1.
3. Если , то
. Действительно, X может принять значение 3 с вероятностью 0, 2 и значение 4 с вероятностью 0, 1; следовательно, одно из этих значений, безразлично какое, X может принять (по теореме о сложении вероятностей несовместных событий) с вероятностью
.
4. Если , то
. Действительно, X может принять значение 3 с вероятностью 0, 2, значение 4 с вероятностью 0, 1 и значение 7 с вероятностью 0, 4; следовательно, одно из этих значений, безразлично какое, X может принять (по теореме о сложении вероятностей несовместных событий) с вероятностью
.
6. Если , то
. Действительно, событие
достоверно и вероятность его равна единице.
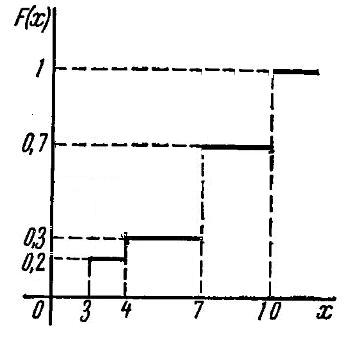
#262
Дана функция распределения непрерывной случайной величины X
Найти плотность распределения f(x).
Решение.
Плотность распределения равна первой производной от функции распределения:
:
При x=0 производная
не существует.
#263
Дана функция распределения непрерывной случайной величины X
Найти плотность распределения f(x).
Решение.
Плотность распределения равна первой производной от функции распределения:
:
При x=0 производная
не существует.
#264
Непрерывная случайная величина X задана плотностью распределения в интервале
; вне этого интервала
. Найти вероятность того, что X примет значение, принадлежащее интервалу
.
Решение
Воспользуемся формулой . По условию
,
и
. Следовательно, искомая вероятность
#265
Непрерывная случайная величина X задана плотностью распределения в интервале
; вне этого интервала
. Найти вероятность того, что X примет значение, принадлежащее интервалу
.
Решение
Воспользуемся формулой . По условию
,
и
. Следовательно, искомая вероятность
#266
Плотность распределения непрерывной случайной величины Х в интервале (-π /2, π /2) равна f(x)=(2/π )*cos2x; вне этого интервала f(x)=0. Найти вероятность того, что в трех независимых испытаниях Х примет ровно два раза значение, заключенное в интервале (0, π /4).
Решение.
Воспользуемся формулой Р(a< X< b)=abfxdx. По условию а=0, b=π /4, f(x)=(2/π )*cos2x. Следовательно, искомая вероятность
Р(0< X< π /4)=(2/π )*0π /4cos2xdx=2π 0π 4cos2x+12dx=1π 12+π 4=π +24π.
Ответ: π +24π.
#267
Задана плотность распределения непрерывной случайной величины Х:
fx=0, при x≤ 0cosx, при 0< x≤ π 20, при x≥ π 2.
Найти функцию распределения F(x).
Решение.
Используем формулу
F(x)=-∞ xfxdx.
Если х ≤ 0, то f(x)=0, следовательно,
F(x)=-∞ 00dx=0.
Если 0< x≤ π 2, то
F(x)=-∞ 00dx+0xcosxdx=sinx.
Если x≥ π 2, то
F(x)=-∞ 00dx+0π 2cosxdx+π 2x0dx=sinx|0π 2=1.
Итак, искомая функция распределения
Fx=0, при x≤ 0sinx, при 0< x≤ π 21, при x> π 2.
#268
Задана плотность распределения непрерывной случайной величины Х:
Fx=0, при x≤ 0sinx, при 0< x≤ π 20, при x> π 2.
Найти функцию распределения F(x).
Решение.
Используем формулу
F(x)=-∞ xfxdx.
#271
Плотность распределения непрерывной случайной величины Х задана на всей оси Ох равеством . Найти постоянный параметр С.
Решение. Плотность распределения должна удовлетворять условию
. Потребуем, чтобы это условие выполнялось для заданной функции:
.
Отсюда
. (*)
Найдем сначала неопределенный интеграл:
.
Затем вычислим несобственный интеграл:
Таким образом,
(**)
Подставив (**) в (*), окончательно получим .
#272
Плотность распределения непрерывной случайной величины задана на всей оси
равенством
Найти постоянный параметр С.
Решение. Плотность распределения должна удовлетворять условию
. Потребуем, чтобы это условие выполнялось для заданной функции:
.
Отсюда
. (*)
Найдем сначала неопределенный интеграл:
.
Затем вычислим несобственный интеграл:
Таким образом,
(**)
Подставив (**) в (*), окончательно получим .
#273
Плотность распределения непрерывной случайной величины X в интервале равна
; вне этого интервала f(х) = 0. Найти постоянный параметр С.
Решение. Плотность распределения должна удовлетворять условию
, но так как f(x) вне интервала
равна 0 достаточно, чтобы она удовлетворяла:
Потребуем, чтобы это условие выполнялось для заданной функции:
.
Отсюда
. (*)
Найдем сначала неопределенный интеграл:
.
Затем вычислим несобственный интеграл:
(**)
Подставив (**) в (*), окончательно получим .
#274
Плотность распределения непрерывной случайной величины Х задана в интервале равенством
; вне этого интервала f(х) = 0. Найти постоянный параметр С.
Решение. Плотность распределения должна удовлетворять условию
, но так как f(x) вне интервала
равна 0 достаточно, чтобы она удовлетворяла:
Потребуем, чтобы это условие выполнялось для заданной функции:
.
Отсюда
. (*)
Найдем сначала неопределенный интеграл:
.
Затем вычислим несобственный интеграл:
(**)
Подставив (**) в (*), окончательно получим .
#275
Случайная величина X задана плотностью распределения ƒ (x) = 2x в интервале (0, 1); вне этого интервала ƒ (x) = 0. Найти математическое ожидание величины X.
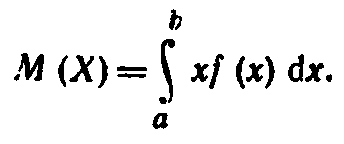 Решение. Используем формулу
Решение. Используем формулу
Подставив a = 0, b = 1, ƒ (x) = 2x, получим
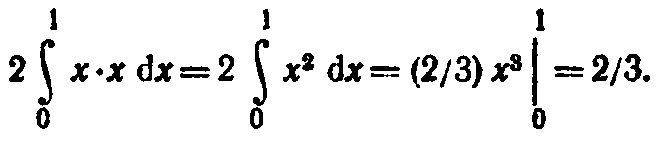
М (Х) =
Ответ: 2/3.
#276
Случайная величина X задана плотностью распределения ƒ (x) = (1/2)x в интервале (0; 2); вне этого интервала ƒ (x) = 0. Найти математическое ожидание величины X.
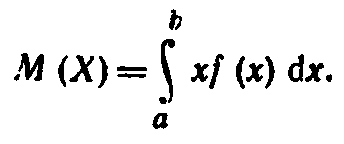 Решение. Используем формулу
Решение. Используем формулу
Подставив a = 0, b = 2, ƒ (x) = (1/2)x, получим
М (Х) = 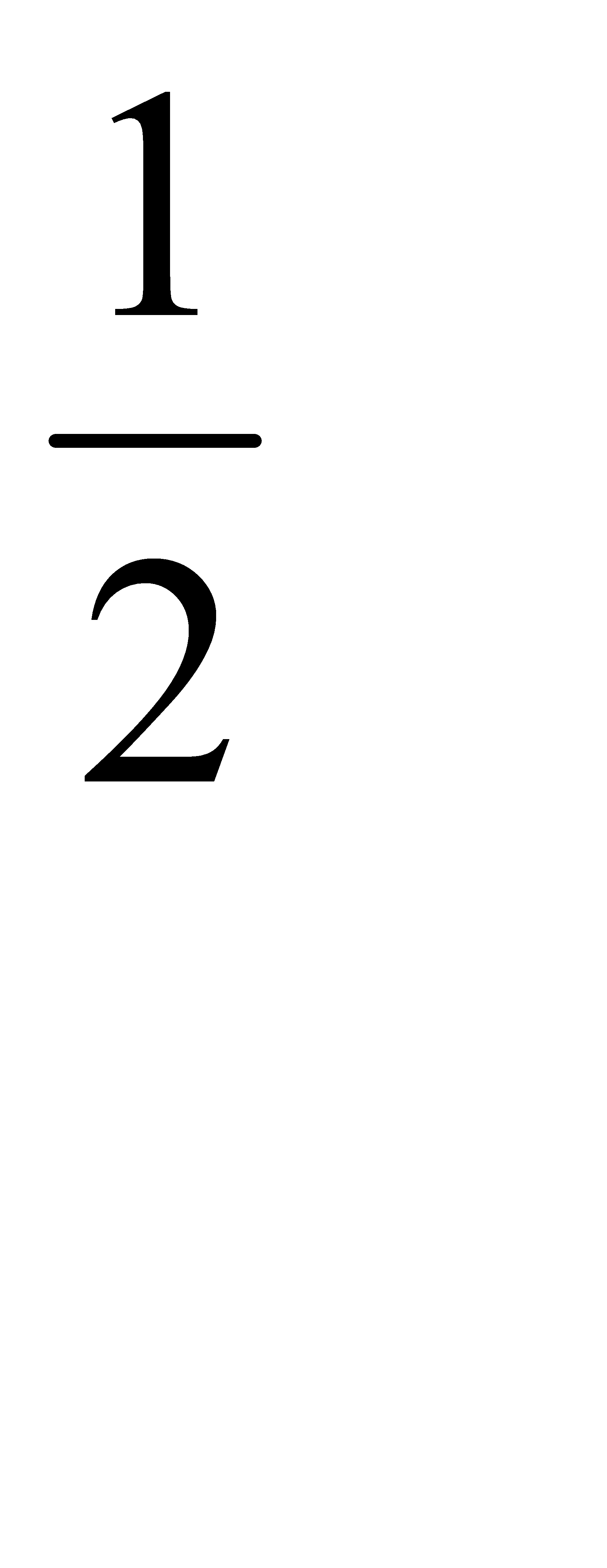
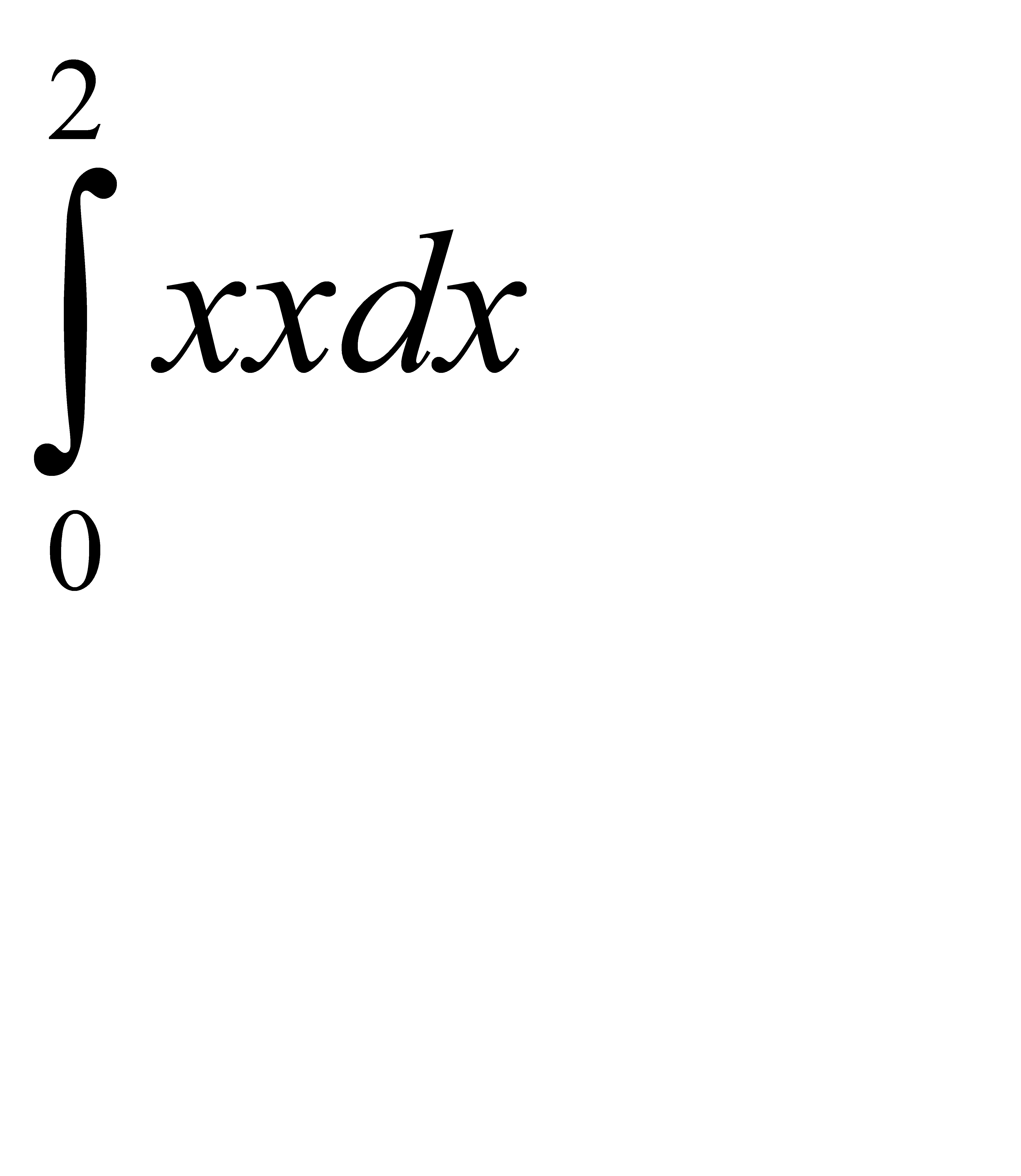 = 4/3
= 4/3
Ответ: 4/3.
#277
Случайная величина X в интервале ( –с, с) задана плотностью распределения
 ƒ (x) = ; вне этого интервала ƒ (x) = 0. Найти математическое ожидание величины X.
ƒ (x) = ; вне этого интервала ƒ (x) = 0. Найти математическое ожидание величины X.
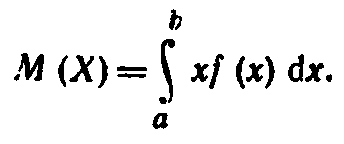 Решение. Используем формулу
Решение. Используем формулу

Подставив a = –с, b = c, ƒ (x) = , получим
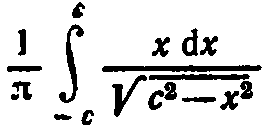
Учитывая, что подынтегральная функция нечетная и пределы интегрирования симметричны относительно начала координат, заключаем, что интеграл равен нулю. Следовательно, М(Х) = 0.
Этот результат можно получить сразу, если принять во внимание, что кривая распределения симметрична относительно прямой х = 0.
Ответ: 0.
#286
Случайная величина Х в интервале (2, 4) задана плотностью распределения f(x)= ; вне этого интервала f(x)=0. Найти моду, математическое ожидание и медиану величины Х.
Решение. Представим плотность распределения в виде . Отсюда видно, что при х=3 плотность распределения достигает максимума; следовательно,
. Кривая распределения симметрична относительно прямой х=3, поэтому
и
.
#287
Случайная величина Х в интервале (3, 5) задана плотностью распределения f(x)= ; вне этого интервала f(x)=0. Найти моду, математическое ожидание и медиану величины Х.
Решение. Представим плотность распределения в виде . Отсюда видно, что при х=3 плотность распределения достигает максимума; следовательно,
. Кривая распределения симметрична относительно прямой х=4, поэтому
и
.
#288
Случайная величина Х в интервале (-1, 1) задана плотностью распределения ; вне этого интервала f(x)=0. Найти: а) моду; б) медиану Х.
Решение. Плотность распределения не имеет максимума, а следовательно мода не существует. Однако легко заметить, что кривая распределения симметрична относительно прямой х=0, следовательно .
#289
Случайная величина Х при х≥ 0 задана плотностью вероятности (распределение Вейбулла) ;
. Найти моду Х.
Решение.
#290
Доказать, что математическое ожидание непрерывной случайной величины заключено между наименьшим и наибольшим её возможными значениями.
Решение. Пусть Х – непрерывная случайная величина, заданная плотностью распределения f(x) на отрезке [a, b]; вне этого отрезка f(x)=0. Тогда a≤ x≤ b. Учитывая, что f(x)=0, получим 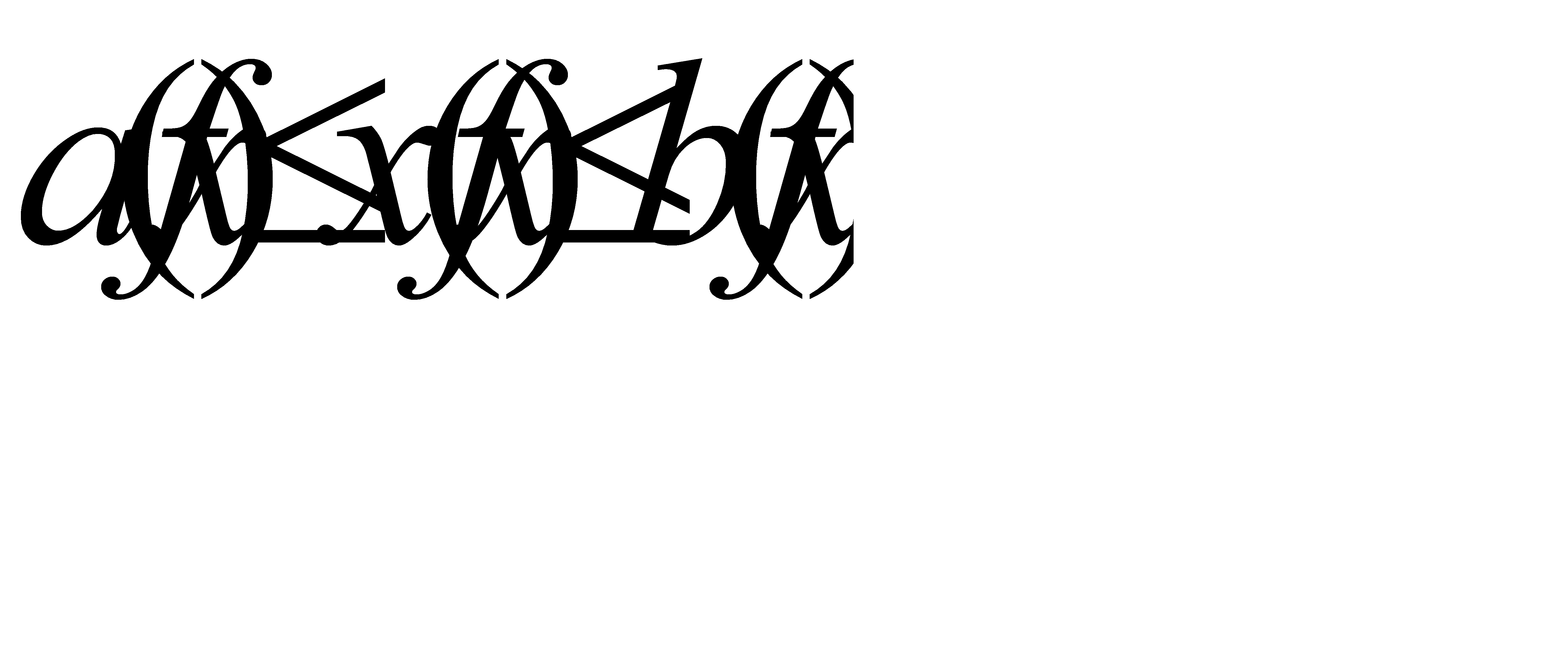 . Проинтегрируем это двойное неравенство в пределах от a до b:
. Проинтегрируем это двойное неравенство в пределах от a до b:
 .
.
Принимая во внимание, что
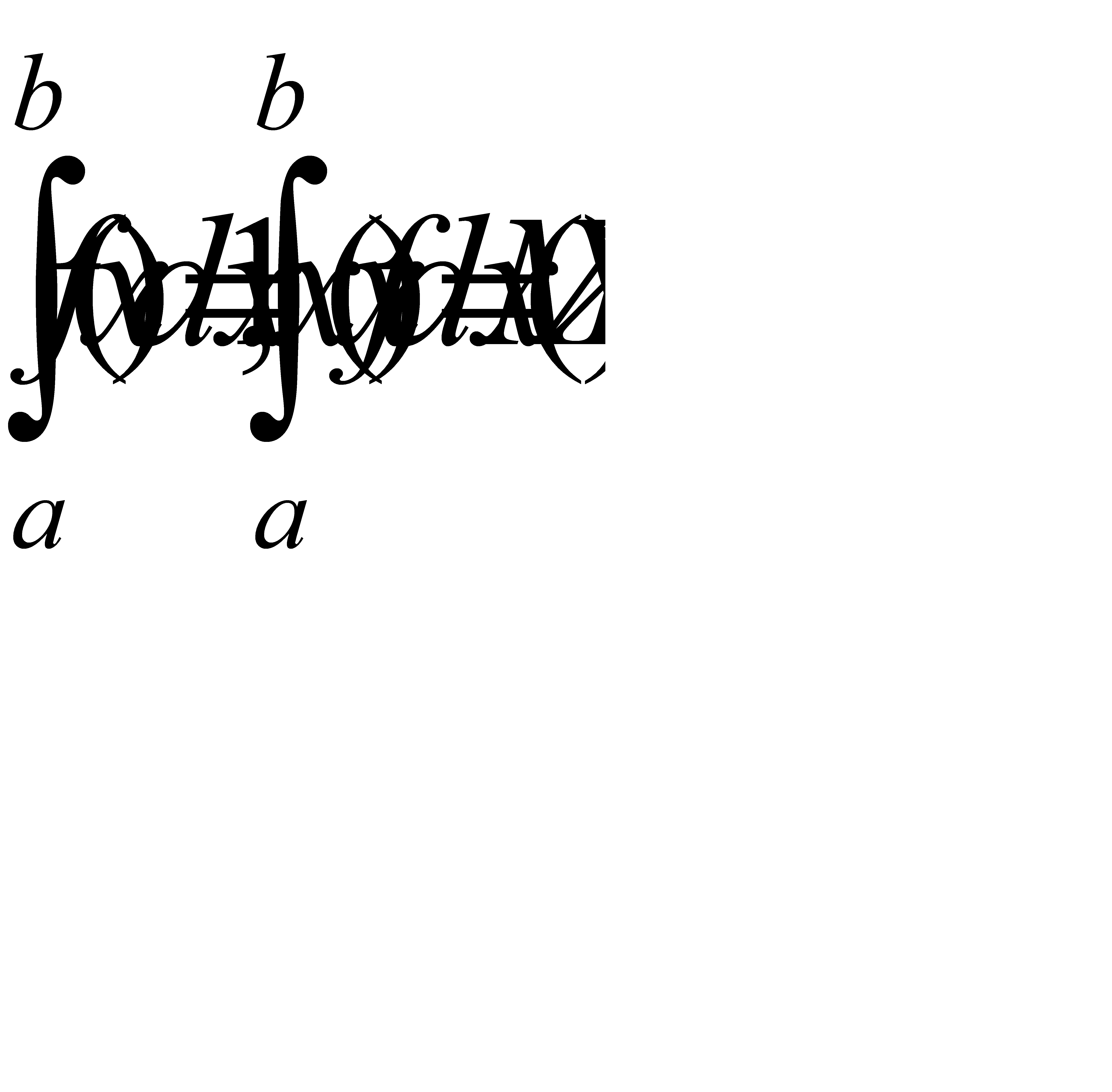 ,
,
Окончательно получим 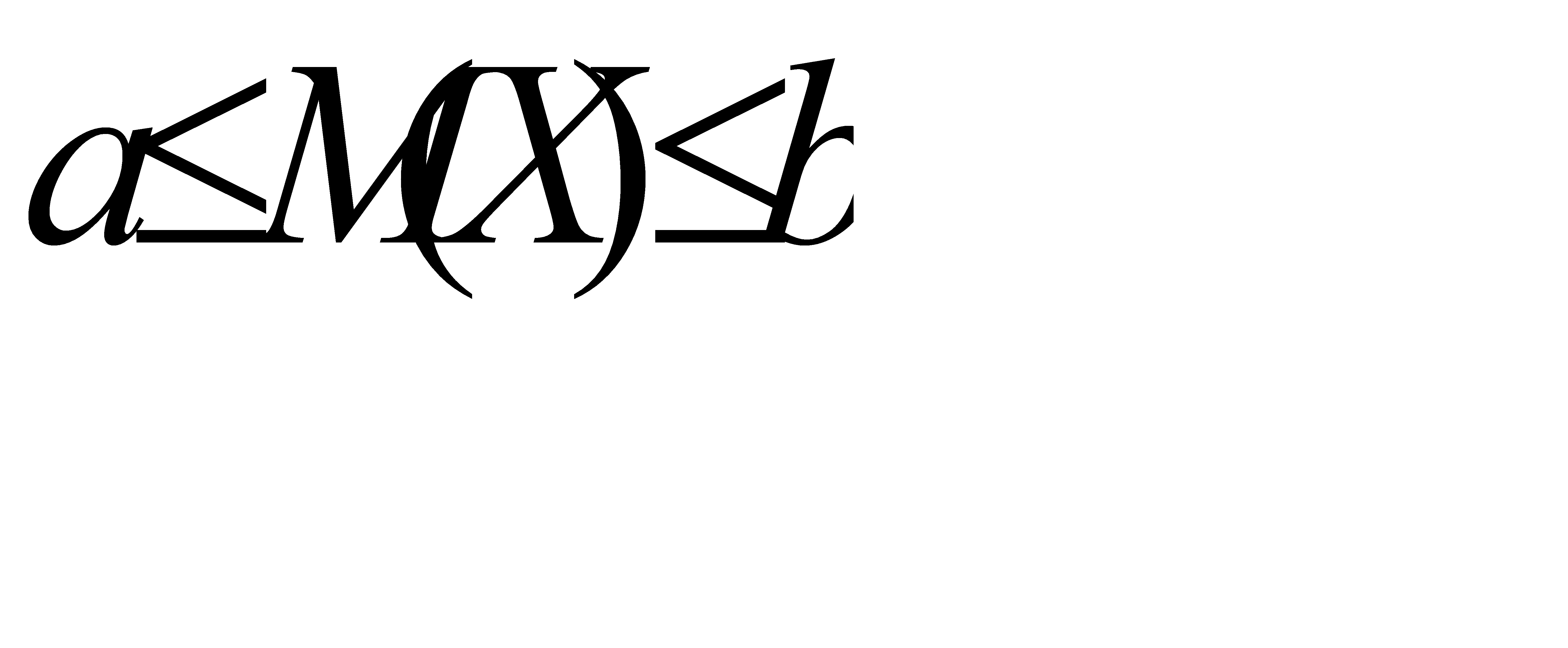 .
.
#291
Доказать, что если  и
и  , то
, то
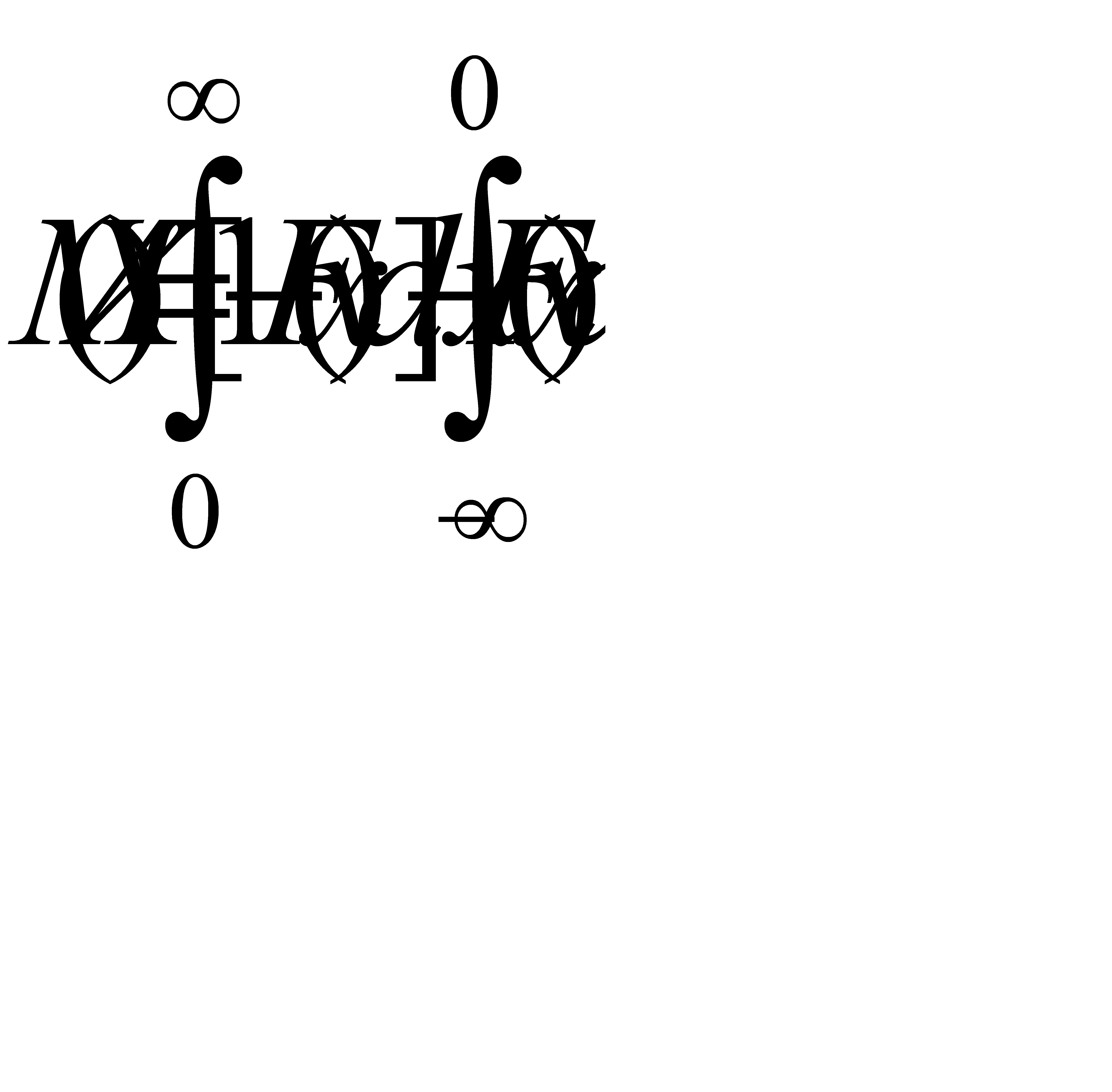 .
.
Решение.
#292
Случайная величина Х в интервале (-c, c) задана плотностью распределения 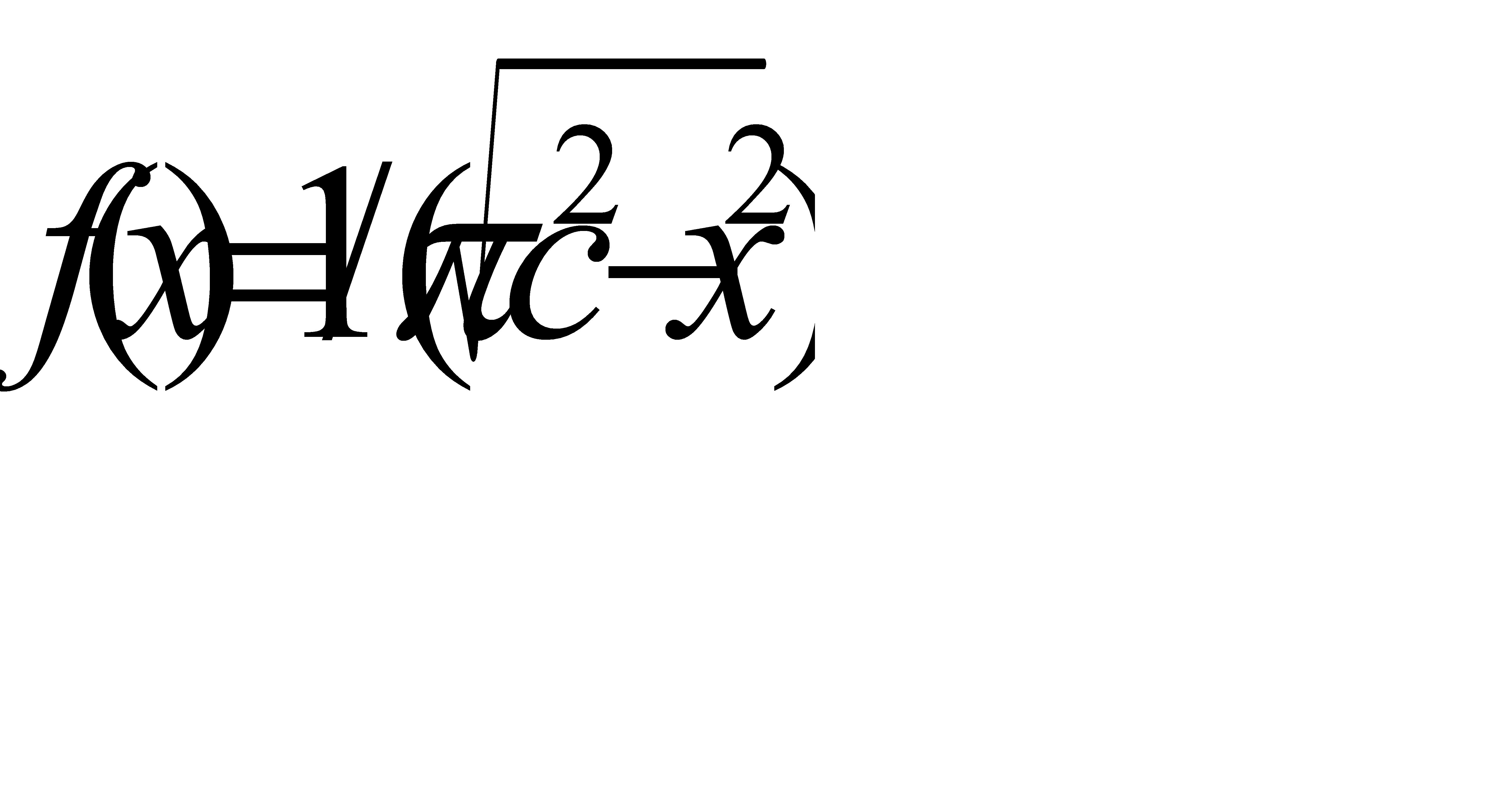 , вне этого интервала f(x)=0. Найти дисперсию Х.
, вне этого интервала f(x)=0. Найти дисперсию Х.
Решение. Будем искать дисперсию по формуле
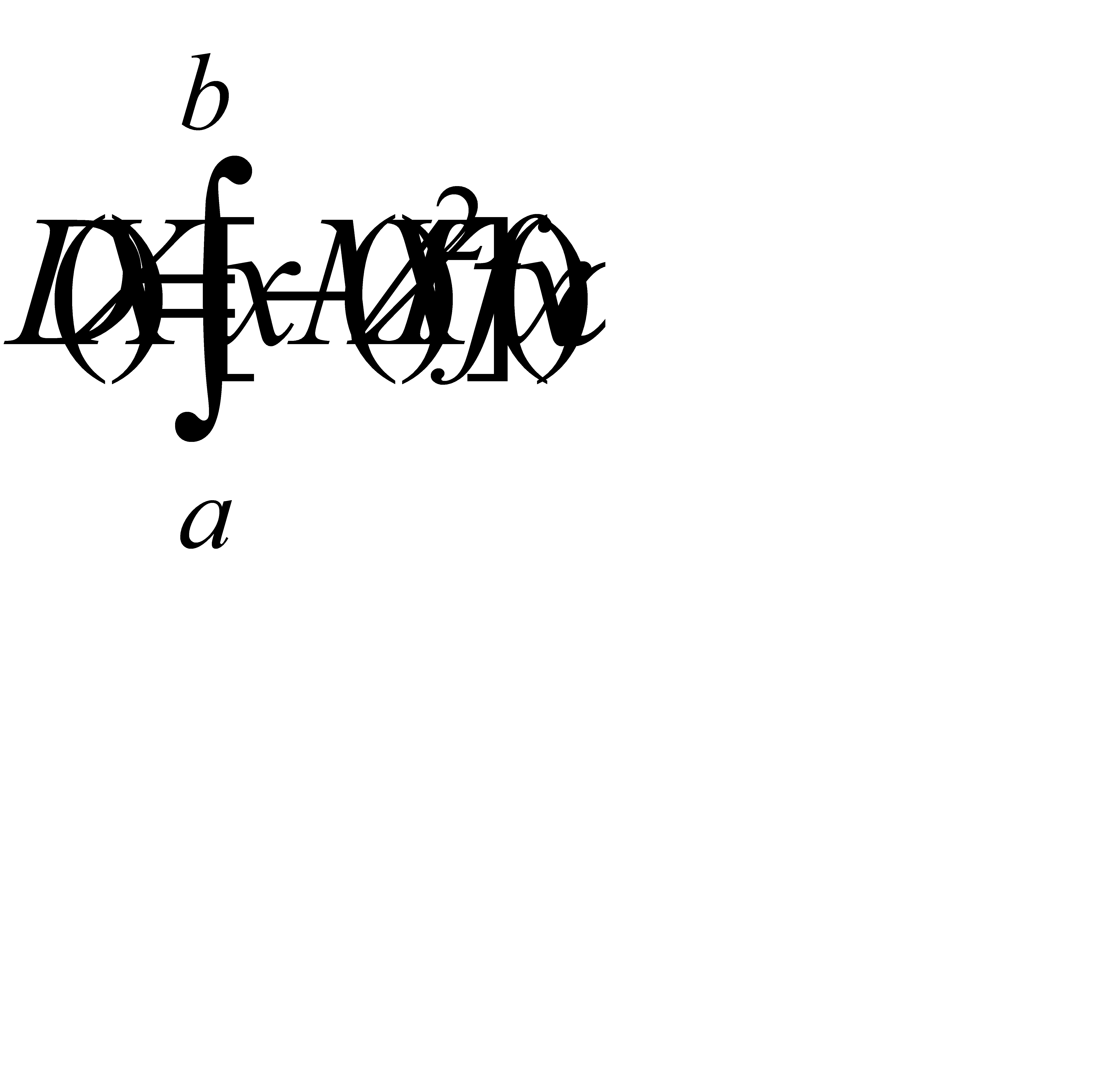 .
.
Подставляя М(Х)=0, получим
 .
.
Сделав подстановку x=csint, окончательно имеем D(X)=c2 /2.
#293
Условие задачи:
Случайная величина Х в интервале (-3, 3) задана плотностью распределения
f(x) = 1/(π 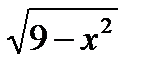 ); вне этого интервала f(x) = 0. а) Найти дисперсию Х; б) Что вероятнее: в результате испытания окажется Х > 1 или Х < 1?
); вне этого интервала f(x) = 0. а) Найти дисперсию Х; б) Что вероятнее: в результате испытания окажется Х > 1 или Х < 1?
Решение задачи:
а) Будем искать дисперсию по формуле:
D(x) = 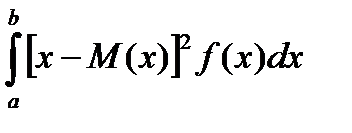 ,
,
где М(x) – математическое ожидание величины Х, вычисляемое по формуле:
М(x) = 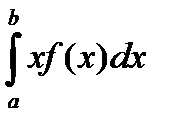
Подставим a = -3, b = 3, f(x) = 1/(π 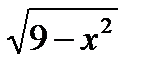 ), получим:
), получим:
M(x) = 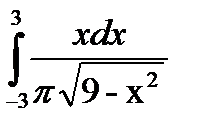
Учитывая, что подынтегральная функция нечетная и пределы интегрирования симметричны относительно начала координат, заключаем, что интеграл равен нулю, т. е. M(x) = 0. Подставляя это значение в формулу для вычисления дисперсии, получим:
D(x) = 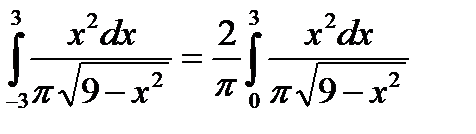
Сделаем замену x = 3sint, dx = 3costdt, тогда окончательно имеем D(x) = 9/2.
б) Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), определяется равенством:
P (a < x < b) = 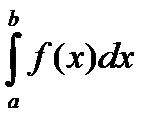
Тогда P (-3 < x < 1) = 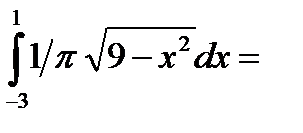 0, 5 + (1/π )arcsin(1/3)
0, 5 + (1/π )arcsin(1/3)
P (1 < x< 3) = 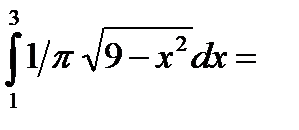 0, 5 - (1/π )arcsin(1/3)
0, 5 - (1/π )arcsin(1/3)
Получаем, что вероятнее в результате испытания окажется x< 1.
#294
Условие задачи:
Доказать, что дисперсию непрерывной случайной величины X можно вычислить по формуле:
D(X) = 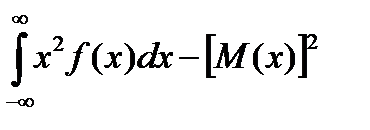
Указание: Воспользоваться формулой
D(X) = 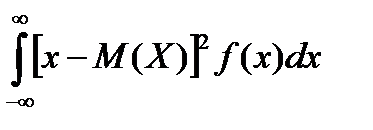 (1)
(1)
и равенствами 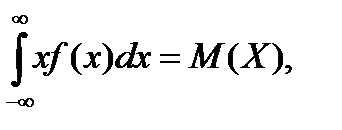
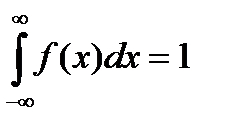 . (2)
. (2)
Решение задачи:
Дисперсия непрерывной случайной величины Х ищется по формуле:
D(X) = 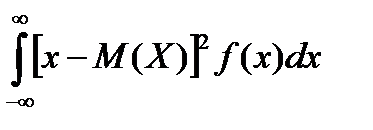
Преобразуем эту формулу следующим образом:
D(X) = 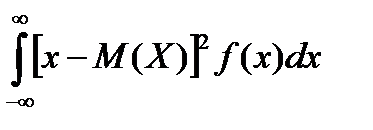 =
= 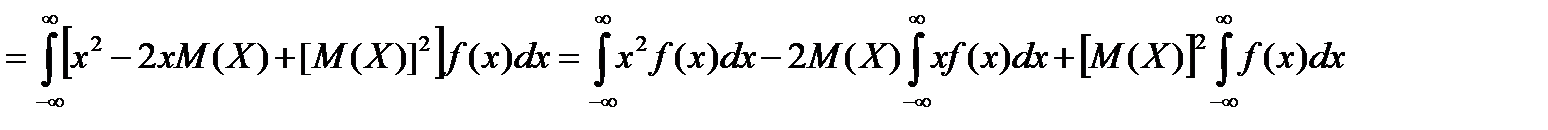
Воспользовавшись равенствами (2), получим:
D(X) = 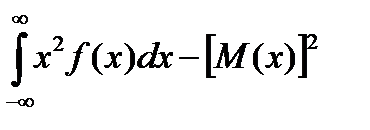
Ч. т. д.
#295
Условия задачи:
Случайная величина X в интервале (0, π ) задана плотностью распределения
f(x) = 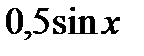 .
.
Вне этого интервала f(x) = 0. Найти дисперсию X.
Решение задачи:
Найдем дисперсию по формуле:
D(X) = 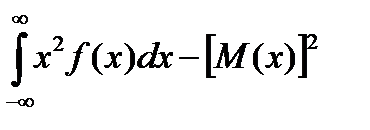
Подставив сюда M(Х) = π /2 (кривая распределения симметрична относительно прямой x = π /2), а = 0, b = π , f(x) = 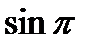 , получим:
, получим:
D(X) = 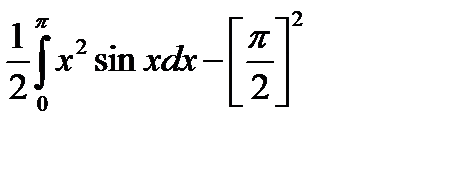
Дважды интегрируя по частям, найдем
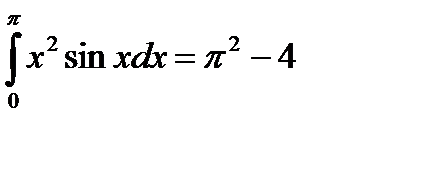
Тогда получим 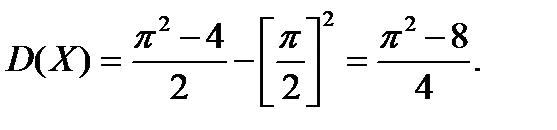
#296
Условие задачи:
Случайная величина X в интервале (0, 5) задана плотностью распределения
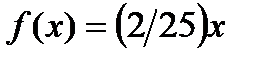 ;
;
вне этого интервала f(x) = 0. Найти дисперсию X.
Решение задачи:
Найдем дисперсию по формуле:
D(X) = 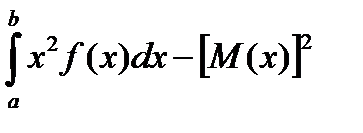
где М(x) – математическое ожидание величины Х, вычисляемое по формуле:
М(X) = 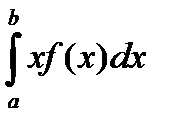
Взяв a = 0, b = 5, 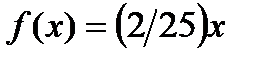 , получим
, получим 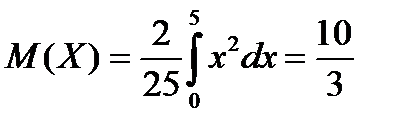
Тогда D(X) = 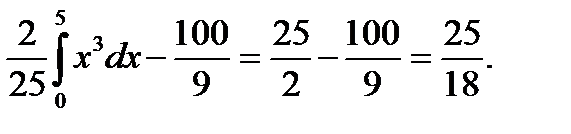
#297
Условие задачи:
Найти дисперсию случайной величины Х, заданной функцией распределения
0 при x ≤ -2
F(x) = 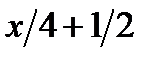 при -2 < x ≤ 2
при -2 < x ≤ 2
1 при x > 2.
Решение задачи:
Найдем плотность распределения
0 при x ≤ -2
f(x) = F’(x) = ¼ при -2 < x ≤ 2
0 при x > 2
Найдем математическое ожидание по формуле
М(X) = 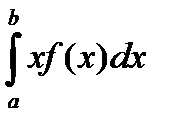
M(X) = 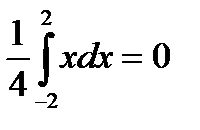 ,
,
т. к. подынтегральная функция нечетная, и пределы симметричны относительно начала координат.
Найдем искомую дисперсию по формуле:
D(X) = 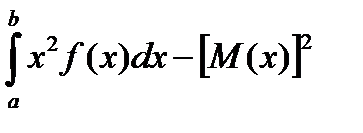
D(X) = 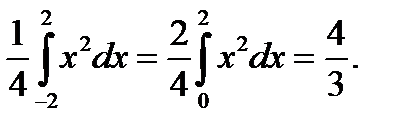
#298
Условие задачи:
Случайная величина задана функцией распределения
F(x) = 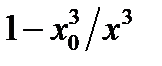 при x ≥
при x ≥ 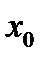 (
( 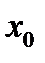 > 0),
> 0),
0 при x< 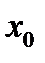 .
.
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение X.
Указание: Найти сначала плотность распределения, использовать формулу:
D(X) = 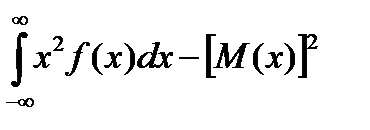
Решение задачи:
Найдем плотность распределения:
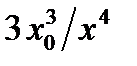 при x ≥
при x ≥ 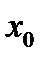 (
( 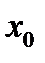 > 0),
> 0),
f(x) = F’(x) = 0 при x< 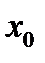 .
.
Найдем математическое ожидание по формуле
М(X) = 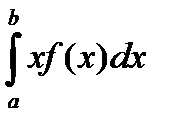
M(X) = 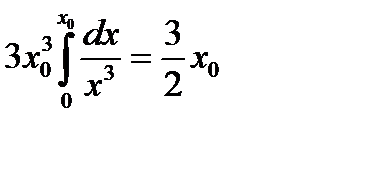
Найдем дисперсию по формуле:
D(X) = 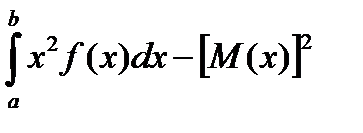
D(X) = 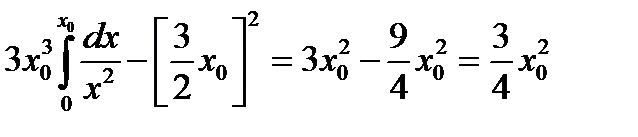
Среднее квадратическое отклонение случайной величины X находится по формуле:
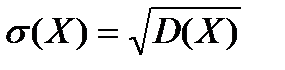
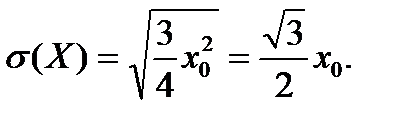
#299
Условие задачи:
Случайная величина X в интервале (0, π ) задана плотностью распределения 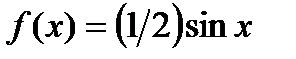 ; вне этого интервала
; вне этого интервала 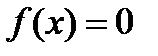 . Найти дисперсию функции
. Найти дисперсию функции 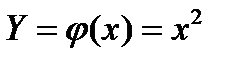 , не находя предварительно плотности распределения Y.
, не находя предварительно плотности распределения Y.
Решение задачи:
Для вычисления дисперсии используем формулу:
D[φ (x)] = 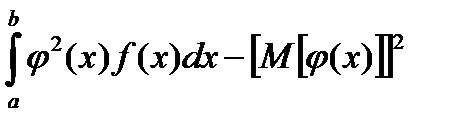
Подставив 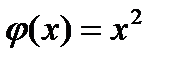 ,
, 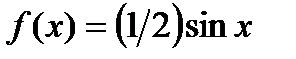 , a = 0, b = π, получим
, a = 0, b = π, получим
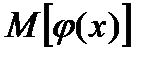 = M[
= M[ 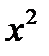 ] =
] = 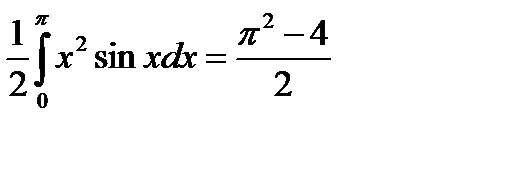
Тогда 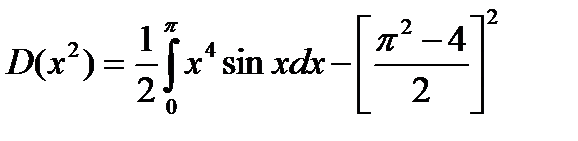
Интегрируя по частям, найдем 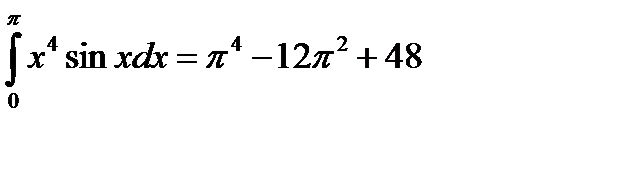 .
.
Тогда 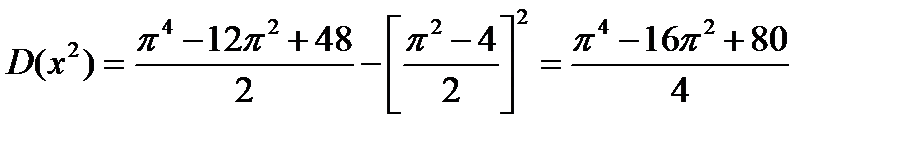 .
.
#300
Условия задачи:
Случайная величина X задана плотностью распределения 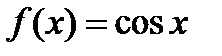 в интервале (0, π /2); вне этого интервала
в интервале (0, π /2); вне этого интервала 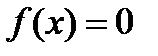 . Найти дисперсию функции
. Найти дисперсию функции 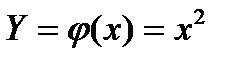 , не находя предварительно плотности распределения Y.
, не находя предварительно плотности распределения Y.
Указание: Использовать формулу:
D[φ (x)] = 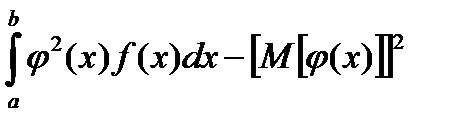
и то, что M( 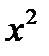 ) =
) = 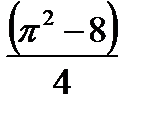 (см. задачу 283).
(см. задачу 283).
Решение задачи:
Для вычисления дисперсии используем формулу:
D[φ (x)] = 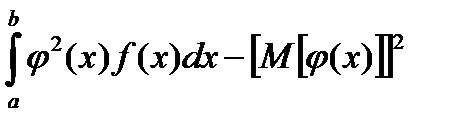
Подставив 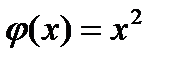 ,
, 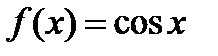 , a = 0, b = π /2, имея M(
, a = 0, b = π /2, имея M( 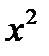 ) =
) = 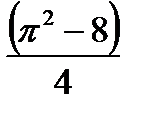 , получим
, получим
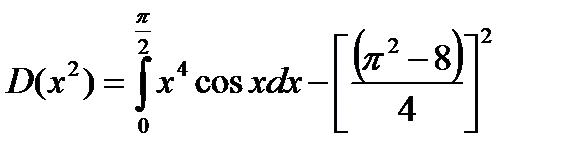
Интегрируя по частям, найдем 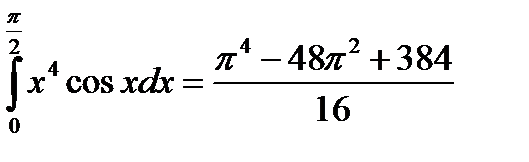 .
.
Тогда 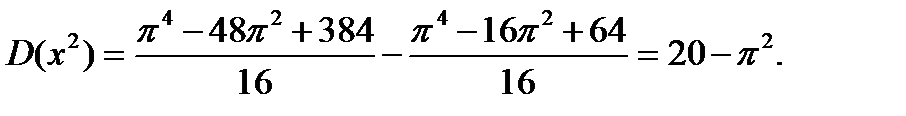
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|