
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
PA(B) ≥ 1 - P(B) / P(A)
#1.
Брошены две игральные кости. Найти вероятность того, чтосумма очков на выпавших гранях – четная, причем на гранях хотя бы одной из костей появится шестерка.
Решение:
На выпавшей грани «первой» игральной кости может появиться одно очко, два очка, …, шесть очков. Аналогичные шесть элементарных исходов возможны и при бросании другой кости. Каждый из исходов бросания «первой» может сочетаться с каждым из исходов бросания «второй». Таким образом общее число возможных элементарных исходов испытания равно 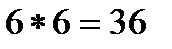 . Эти исходы образуют полную группу и в силу симметрии костей равновозможны.
. Эти исходы образуют полную группу и в силу симметрии костей равновозможны.
Благоприятствующими интересующему нас событию (хотябы на одной грани появится шестерка, сумма выпавших очков четная) являются следующие пять исходов
1)6, 2 2)6, 4 3)6, 6 4)2, 6 5)4, 6
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех возможных элементарных исходов испытания: 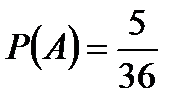
#2.
Решение:
а) Извлеченная стандартная деталь, очевидно, не
могла быть утеряна; могла быть потеряна любая из остальных 30 деталей (21+10—1=30), причем среди них было 20 стандартных (21-1=20). Вероятность того, что была потеряна стандартная деталь, Р= 20/30 = 2/3.
б) Среди 30 деталей, каждая из которых могла быть утеряна, было 10 нестандартных. Вероятность того, что потеряна нестандартная деталь,
Р=10/30=1/3.
Ответ: 1/3
#3
Решение
а) Мы рассматриваем событие:
А – задуманным двузначным числом оказалось случайно названное двузначное число.
Для этого события общее число возможных элементарных исходов n = 90, т. е. количество всех двузначных чисел. А число возможных исходов, благоприятствующих событию m = 1, т. е. только одно двузначное число будет равно задуманному.
Итак, по классическому определению вероятности получаем:
P(A) = m/n = 1/90
б) Мы рассматриваем событие:
А – задуманным двузначным числом оказалось случайно названное двузначное число, цифры которого различны.
Для этого события общее число возможных элементарных исходов n = 81, т. е. количество всех двузначных чисел, цифры которого различны. А число возможных исходов, благоприятствующих событию m = 1, т. е. только одно двузначное число будет равно задуманному.
Итак, по классическому определению вероятности получаем:
P(A) = m/n = 1/81 Ответ: а)1/90; б)1/81
#4
Задание: Указать ошибку «решения» задачи: брошены две игральные кости, найти вероятность того, что сумма очков на костях будет равна 3 (событие  ). решение: Общее число равновозможных исходов испытания равно
). решение: Общее число равновозможных исходов испытания равно 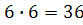 (каждое число очков, выпавших на одной кости, может сочетаться со всеми числами очков, выпавших на другой). Среди этих исходов событию
(каждое число очков, выпавших на одной кости, может сочетаться со всеми числами очков, выпавших на другой). Среди этих исходов событию 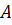 может благоприятствовать только два исхода:
может благоприятствовать только два исхода: 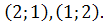 Следовательно, искомая вероятность
Следовательно, искомая вероятность 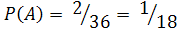 .
.
#5
решение:
Общее число равно равновозможных исходов равно 6*6=36 (Каждое число на одной кости может сочетаться со всеми числами очков, выпавших на другой кости)
А) среди общего количества исходов событию А благоприятствуют только 6: (1. 6), (6, 1), (2, 5), (5, 2), (3, 4), (4, 3) следовательно искомая вероятность 6/36=1/6
Б) среди общего количества исходов событию А благоприятствуют только 6: (2. 6), (6, 2), (3, 5), (5, 3), (4, 4), (4, 4), но в следствии того что разность равна 4 останется только два события: (2, 6) и (6, 2). Следовательно искомая вероятность 2/36=1/18
В) Общее число исходов события А равно 4: (6, 2) (2, 6) (5, 1) (1, 5) (т. к. разность должна быть равна 4). Среди общего количества исходов события А благоприятствуют только 2: (6, 2) и (2, 6). Следовательно искомая вероятность равна 2/4 = ½
Г) среди общего количества исходов событию А благоприятствуют только 4: (1, 4), (4, 1), (3, 2), (2, 3), но в следствии того что произведение равно 4 останется только два события: (1, 4) и (4, 1). Следовательно искомая вероятность 2/36=1/18
#6
Общее число равновозможных исходов равно 1000 (всего столько кубиков). Среди этих исходов благоприятствуют событию 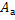 только 384 исхода (64 маленьких кубика имеют одну окрашенную грань на грани большого, граней у куба 6, поэтому
только 384 исхода (64 маленьких кубика имеют одну окрашенную грань на грани большого, граней у куба 6, поэтому 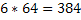 ) следовательно искомая вероятность
) следовательно искомая вероятность 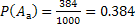 . Благоприятствует событию
. Благоприятствует событию 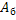 только
только  исходов, т. е.
исходов, т. е. 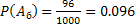 . А событию
. А событию 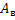 – 8 исходов (только на углах большого куба у маленьких кубиков окрашены 3 грани), т. е.
– 8 исходов (только на углах большого куба у маленьких кубиков окрашены 3 грани), т. е. 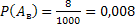 .
.
#7. Монета брошена 2 раза. Найти вероятность того, что хотя бы один раз появится «герб».
Решение: Всего различных случаев выпадения монеты – 4. Обозначим как 1- выпала «решка», 0 – выпал «герб». Тогда можем составить таблицу:
| 1я попытка | 2я попытка |
Т. е. всего удовлетворяющих нас выпадений – 3 из 4. Следовательно, вероятность того, что выпадет хоть один «герб» равна PA= mn= 34;
#8 Число всевозможных исходов эксперимента – 720
(Так как нам важно, в каком порядке извлекаются кубики, то для подсчёта всех возможных исходов необходимо найти все их перестановки, то есть n= 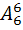 =6! =720)
=6! =720)
Число исходов, удовлетворяющих поставленному условию – 1
(то есть m=1)
Значит шанс, что все кубики извлекутся в нужном порядке - 1/720
( P(a)=m/n=1/720)
Ответ: 1/720
#9 Найти вероятность того, что при бросании трех игральных костей шестерка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой (и не равные 6).
Решение: Общее число элементарных исходов испытания равно числу сочетаний из 6 элементов по 3 с повторениями ( 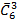 ).
).
Число исходов, благоприятствующих появлению шестерки на одной грани и различного числа очков (не равных 6) на гранях двух других костей, равно числу сочетаний без повторений из 5 элементов по 2 ( 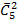 ).
).
Искомая вероятность равна отношению числа исходов, благоприятствующих интересующему нас событию, к общему числу возможных элементарных исходов:
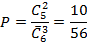
Ответ: 10/56.
#10 В пачке 20 перфокарт, помеченных номерами 101, 102, ... , 120 и произвольно расположенных. Перфораторщица наудачу извлекает две карты. Найти вероятность того, что извлечены перфокарты с номерами 101 и 120.
Решение: Общее число элементарных исходов испытания равно числу сочетаний из 20 элементов по 2 с повторениями ( 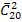 ).
).
Число исходов, благоприятствующих появлению перфокарт с номерами 101 и 120, равно числу сочетаний без повторений из 2 элементов по 2 ( 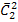 ) = 1.
) = 1.
Искомая вероятность равна отношению числа исходов, благоприятствующих интересующему нас событию, к общему числу возможных элементарных исходов:
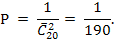
Ответ: 1/190.
#11 В ящике 10 одинаковых деталей, помеченных 1, 2, …, 10. Наудачу извлечены 6 деталей. Найти вероятность того, что среди извлеченных деталей окажутся:
А) деталь № 1;
Б) деталь № 1 и № 2.
Решение.
А) Общее число возможных элементарных исходов равно числу способов, которыми можно извлечь 6 деталей из 10, т. е. 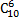 .
.
Найдем число исходов, благоприятствующих интересующему нас событию: среди отобранных 6 деталей есть деталь № 1 и, следовательно, остальные пять деталей имеют другие номера. Число таких исходов, очевидно, равно числу способов, которыми можно отобрать 5 деталей из оставшихся 9, т. е. 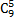 .
.
Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу возможных элементарных исходов: P= 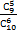 =0, 6.
=0, 6.
Б) Число исходов, благоприятствующих интересующему нас событию (среди отобранных деталей есть детали № 1 и № 2, следовательно, четыре детали имеют другие номера), равно числу способов, которыми можно извлечь четыре детали из оставшихся восьми, т. е. C48. Искомая вероятность P= 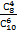 =1/3.
=1/3.
#12 В ящике имеется 15 деталей, среди которых 10
окрашенных. Сборщик наудачу извлекает три детали.
Найти вероятность того, что извлеченные детали окажутся
окрашенными. Решение: Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 3 детали из 15. . Число исходов, благоприятствующих равно числу возможных вариантов извлечения 3 деталей из 10. Искомая вероятность равна отношению С из 15 по 3 деленное на С из 10 по 3.
#13 В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная.
Решение: Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 10 карточек из 100. = 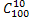 .
.
Число исходов, благоприятствующих равно числу возможных вариантов извлечения 9 карточек. 10ая карточка – это карточка интересующая нас. Это число равно 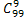 .
.
Искомая вероятность равна отношению P= 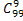 /
/  = 0, 1.
= 0, 1.
#14 В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных.
РЕШЕНИЕ. а) Общее число возможных элементарных исходов испытания равно количеству способов извлечь 4 детали из100, т. е. 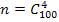 , число благоприятствующих рассматриваемому событию исходов равно количеству способов извлечь 4 не бракованные детали, т. е.
, число благоприятствующих рассматриваемому событию исходов равно количеству способов извлечь 4 не бракованные детали, т. е. 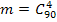 . Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу возможных элементарных исходов:
. Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу возможных элементарных исходов:
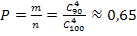 .
.
б) Число благоприятствующих рассматриваемому событию исходов равно количеству способов извлечь 4 бракованные детали, т. е. 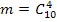 .
.
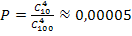 .
.
#15 Решение: Общее число возможных элементарных исходов испытания равно числу вариантов включения двух элементов из пяти, что составляет 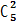 Найдем число исходов, благоприятствующих интересующему нас событию: оба включенных элемента неизношенны, следовательно, все оставшиеся изношены. Чисто таких исходов равно числу способов, которыми можно извлечь два неизношенных элемента из трех:
Найдем число исходов, благоприятствующих интересующему нас событию: оба включенных элемента неизношенны, следовательно, все оставшиеся изношены. Чисто таких исходов равно числу способов, которыми можно извлечь два неизношенных элемента из трех: 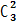
Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу возможных элементарных исходов: 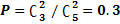
#17
Решение: Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь m деталей из N деталей, т. е.  —числу сочетаний из N элементов по m.
—числу сочетаний из N элементов по m.
Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди m деталей ровно k стандартных): k стандартных деталей можно взять из п стандартных, деталей 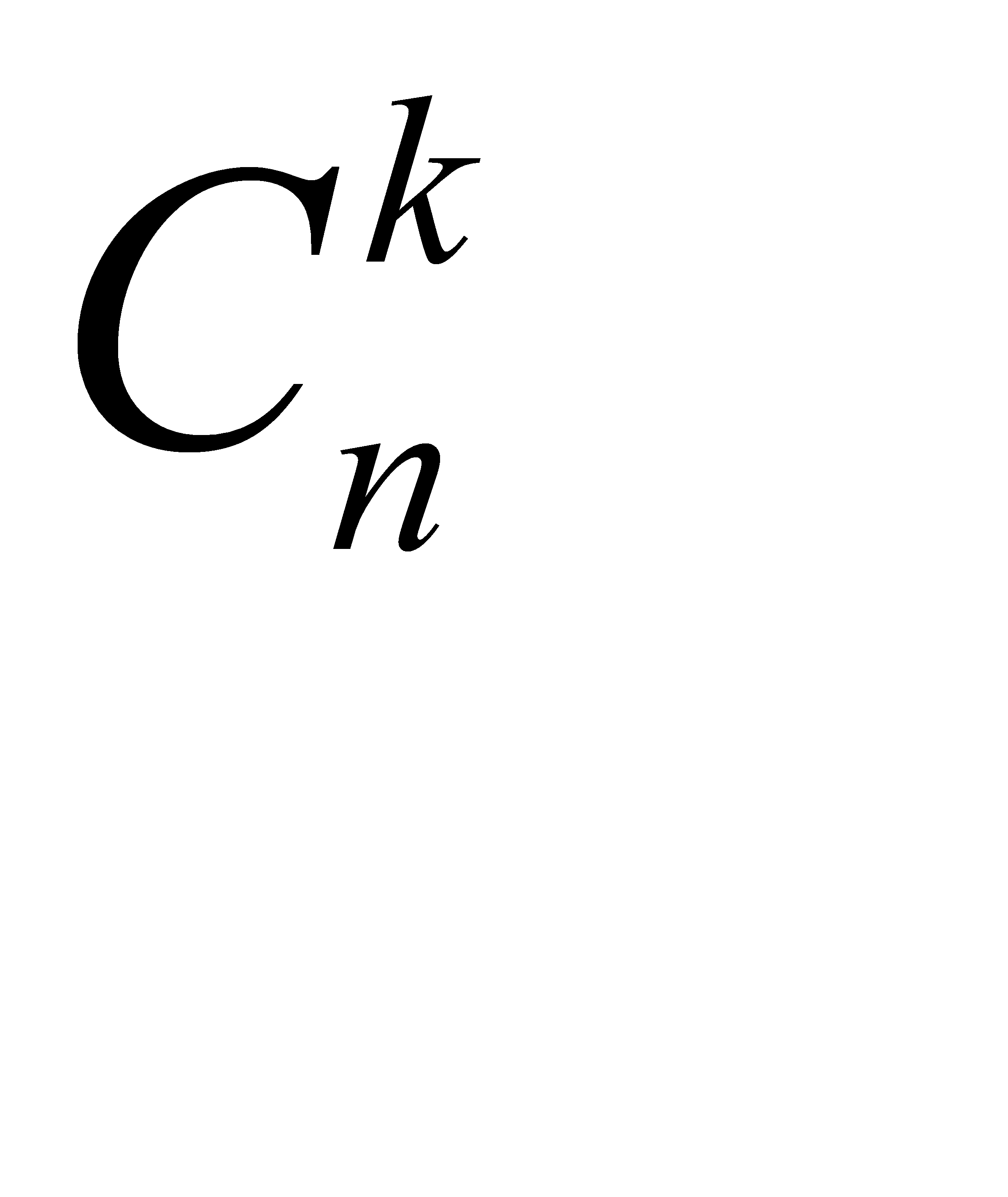 способами; число благоприятствующих исходов равно
способами; число благоприятствующих исходов равно 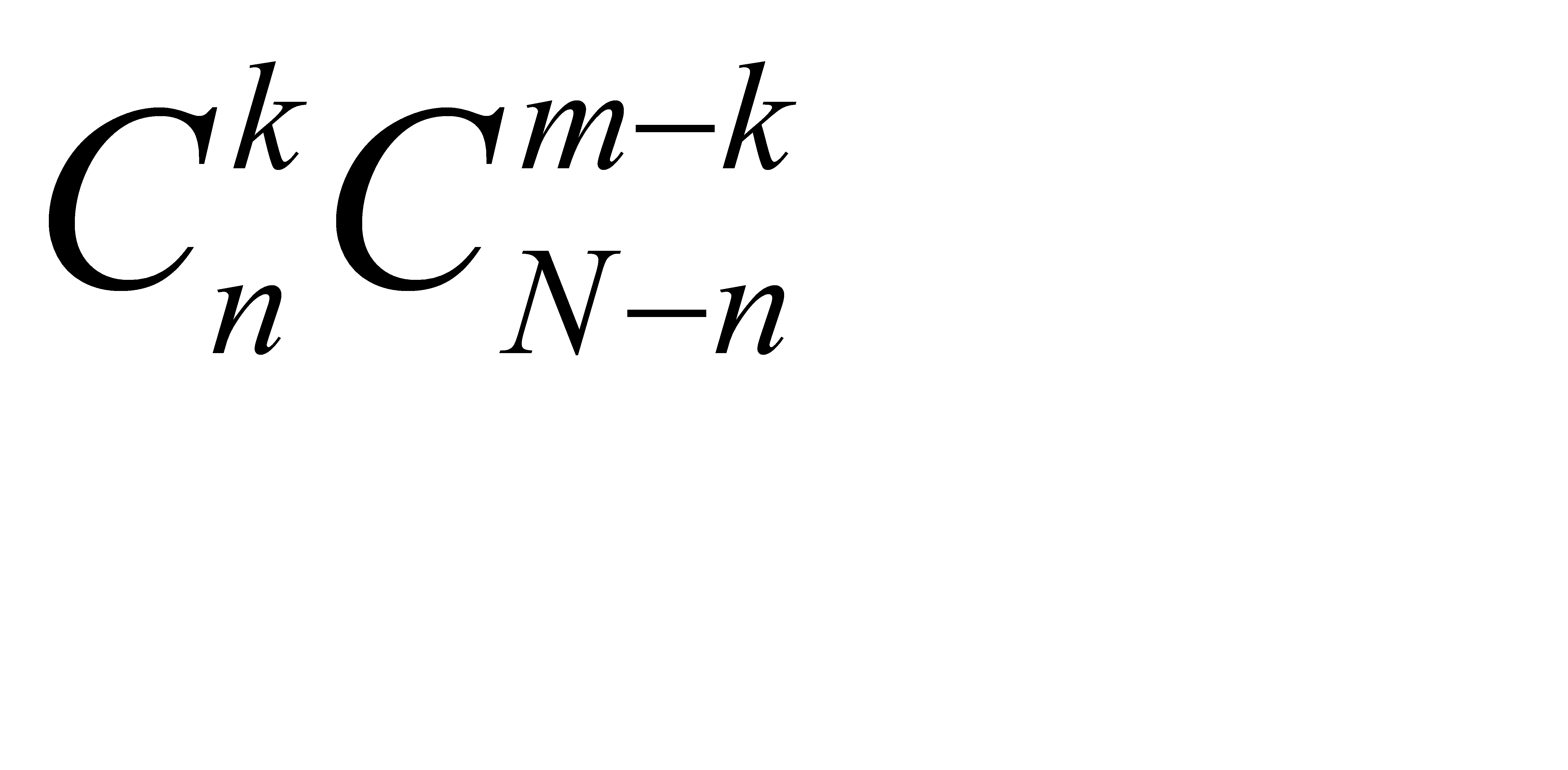
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
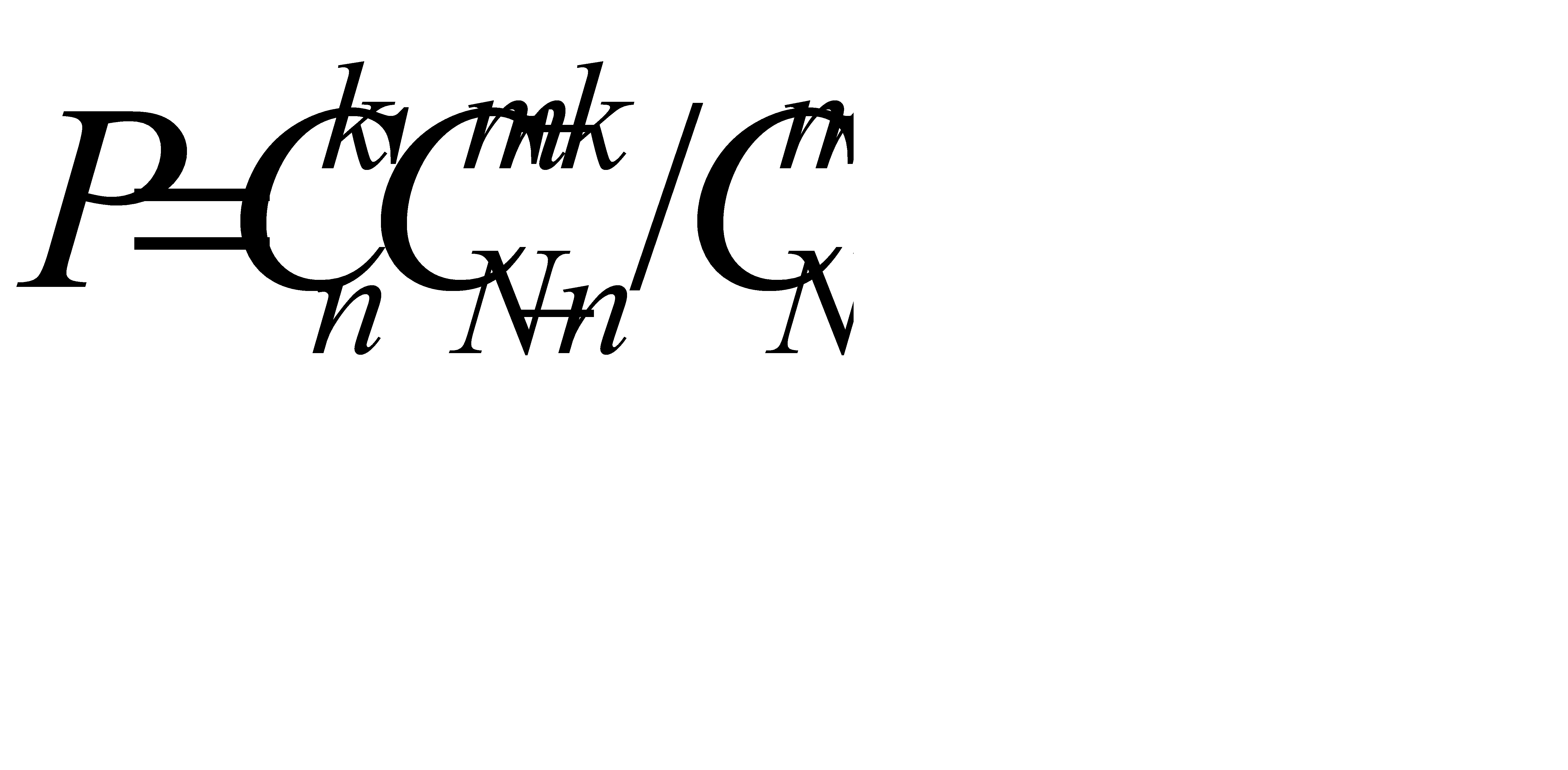
#18 Решение задачи: Общее число равновозможных элементарных исходов испытания равно числу способов отбирания по табельным номерам  человек из
человек из  , т. е числу сочетаний
, т. е числу сочетаний  .
.
Найдем число исходов, благоприятствующих интересующему нас событию: трех из четырех можно отобрать 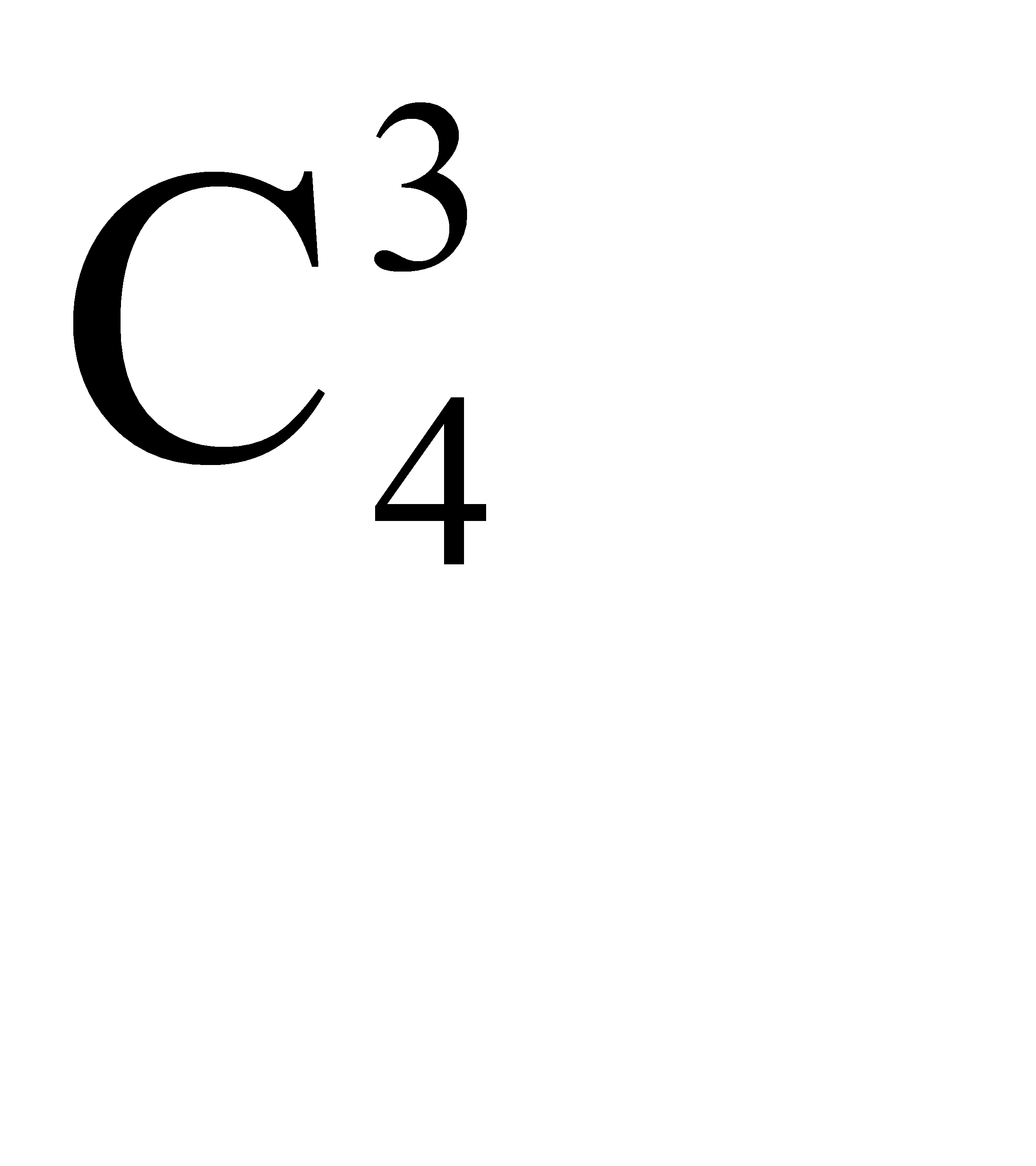 способами. Остальные четыре человека будут мужчинами. Выбор четырех из шести мужчин можно осуществить
способами. Остальные четыре человека будут мужчинами. Выбор четырех из шести мужчин можно осуществить 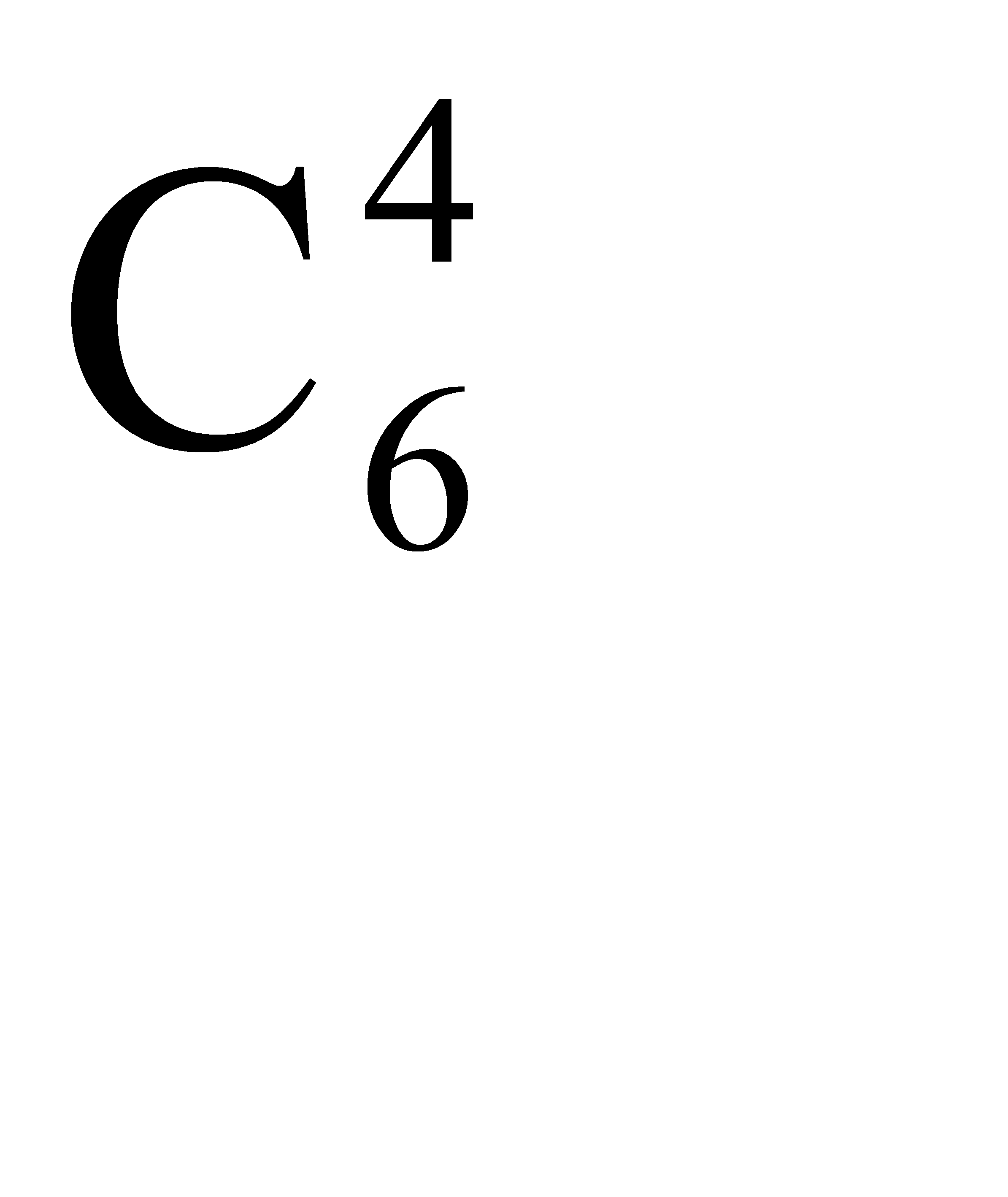 способами. Следовательно число благоприятствующих исходов равно
способами. Следовательно число благоприятствующих исходов равно 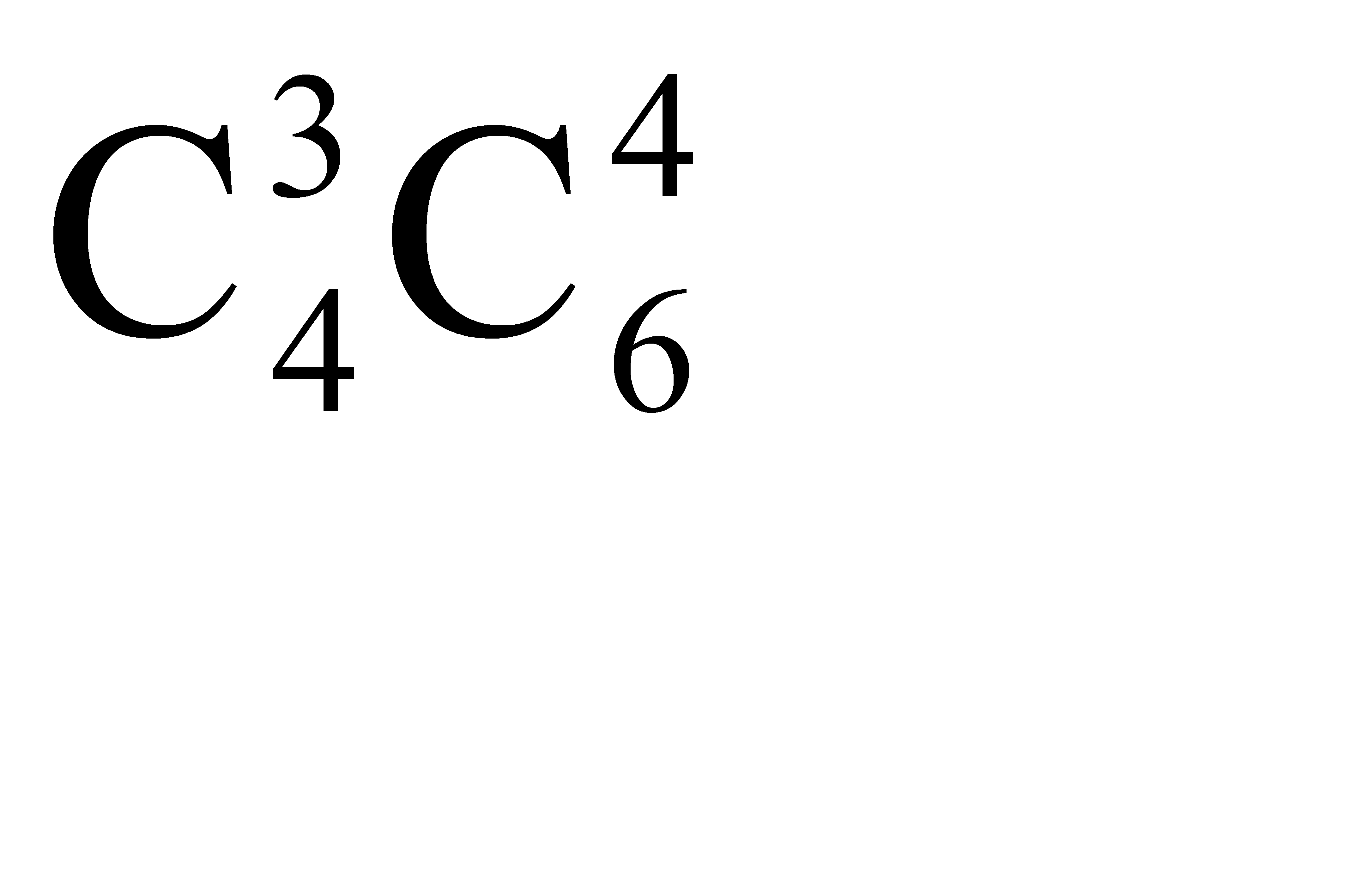 .
.
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех равновозможных элементарных исходов, т. е:
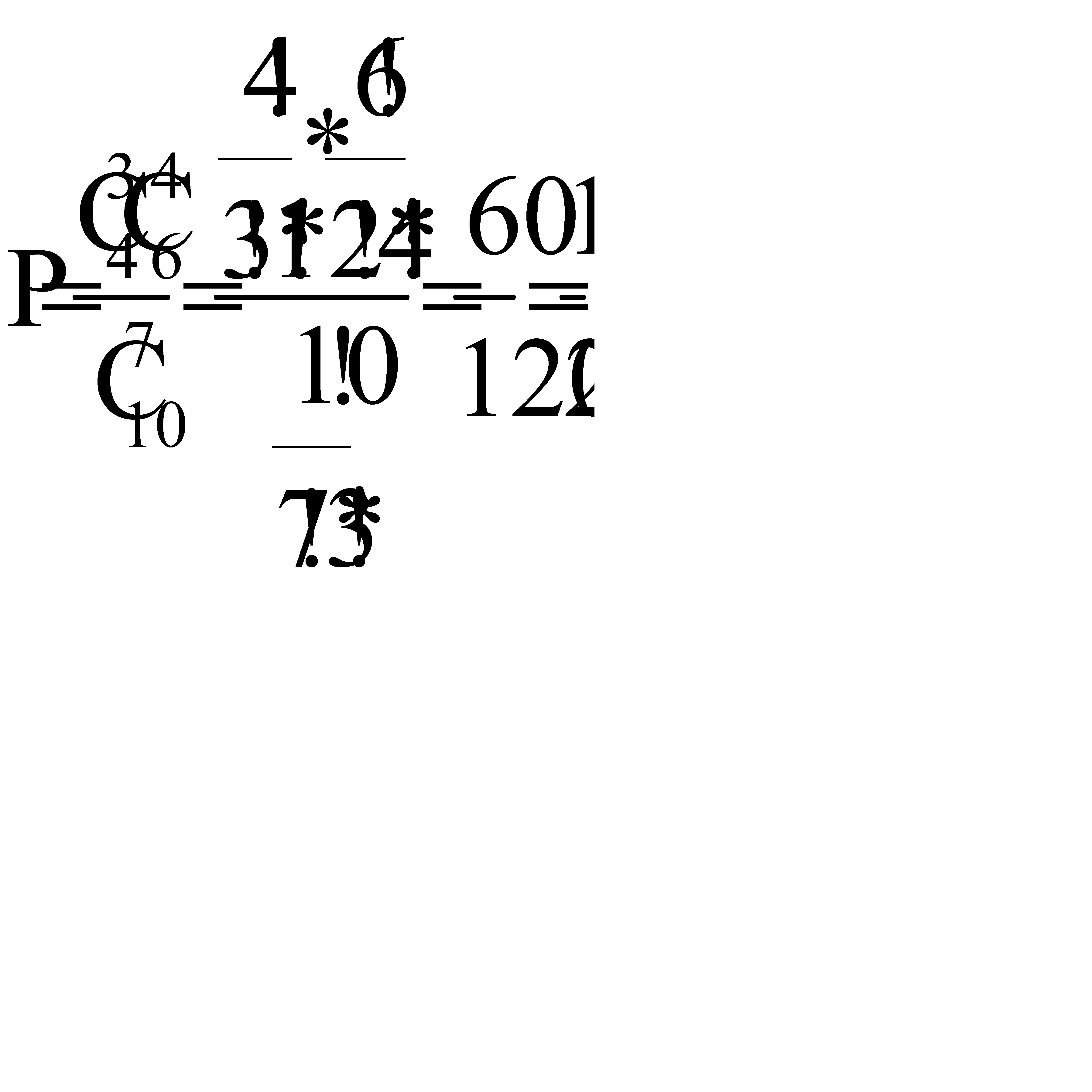
Ответ: 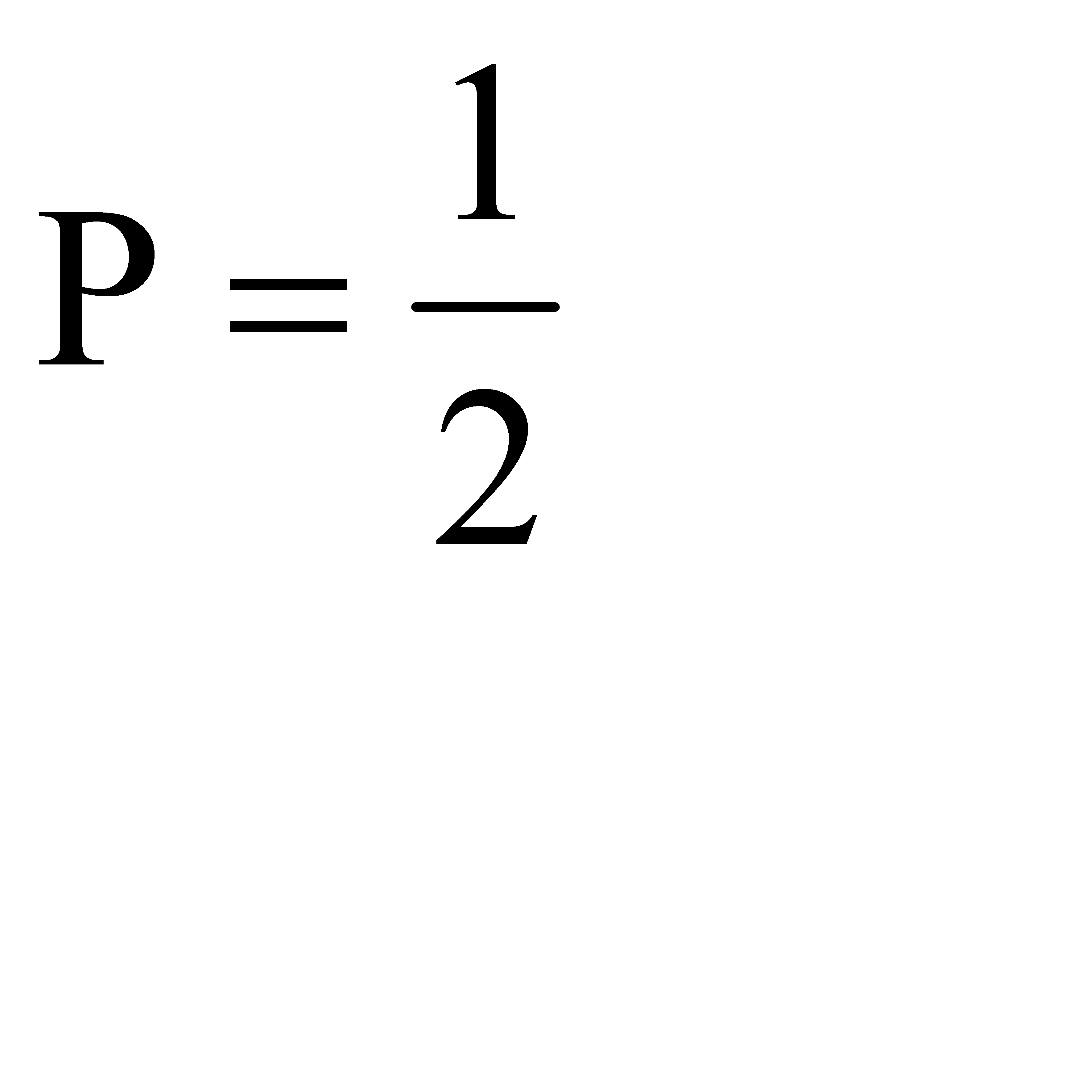
#21 Решение: а)Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь две детали из пяти, и равно числу сочетаний из пяти по два. Одно окрашенное изделие можно взять из трех окрашенных изделий С31 способами. А число способов взять одно неокрашенное изделие из двух неокрашенных равно С21.
Число благоприятствующих условий равно С31 С21. Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов: Р= С31 *С21 /С52=0, 6
б) Р= С32 *С20 /С52=0, 3
в) Р= С31 *С21 /С52 +С32 *С20 /С52=0, 9
# 24
Решение. Относительная частота события А (попадание в цель) равна отношению числа попаданий к числу произведенных выстрелов: 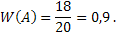
#26
Решение:
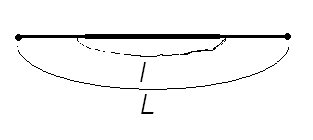
Т. к. вероятность
попадания точки на отрезок
пропорциональна длине отрезка,
и не зависит от его расположения,
то искомую вероятность можно
найти по формуле
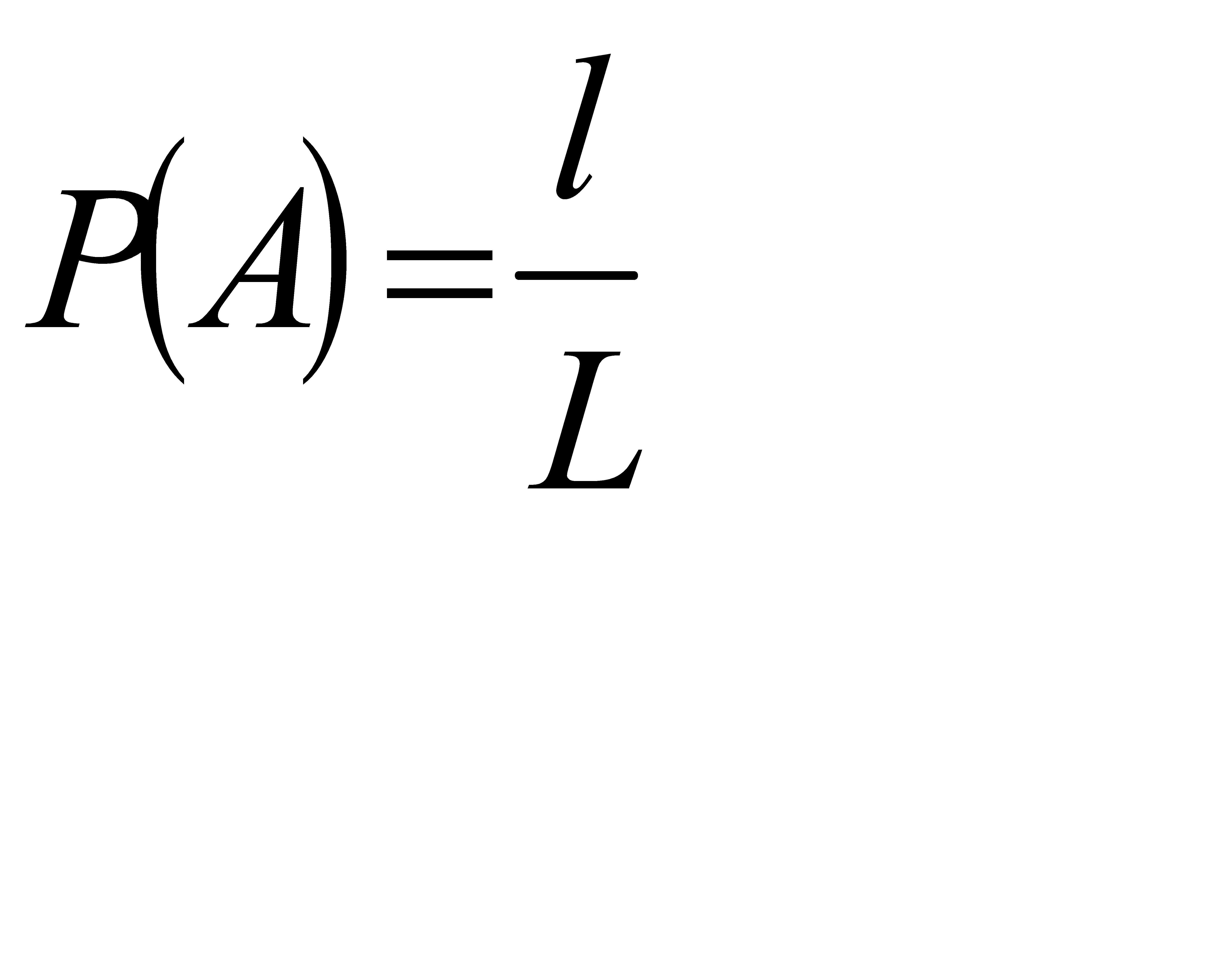
Подставляя наши значения (L=20; l=10) в данную формулу получаем искомую вероятность
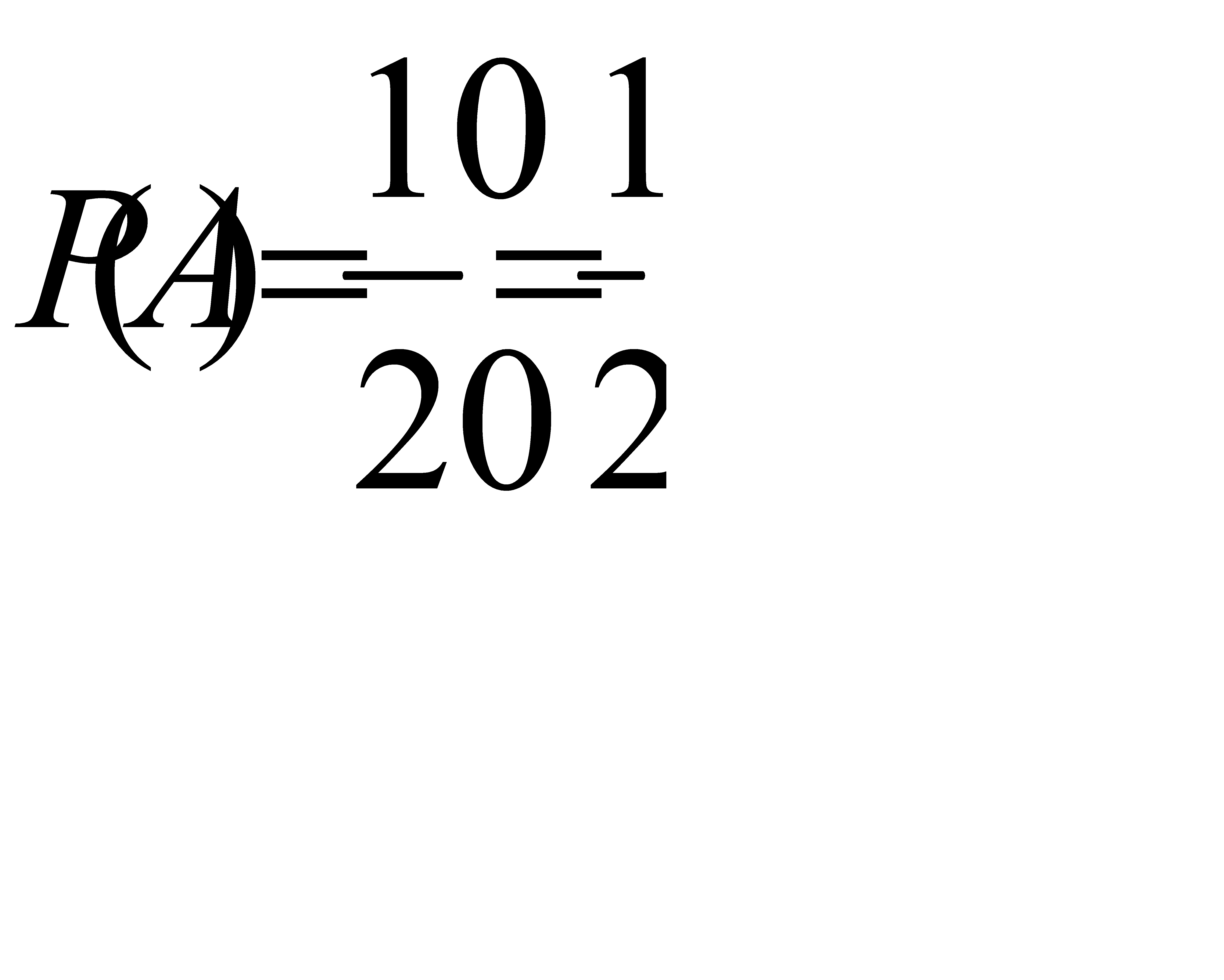
#27
Условие:
На отрезок ОА длины L числовой оси Ох наудачу поставлена точка В(х). Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую чем L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка, и не зависит от его расположения на числовой оси.
Решение:
Разобьём отрезок ОА на 3
отрезка длины L/3. Тогда
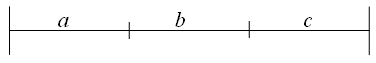 для того чтобы меньший из
для того чтобы меньший из
отрезков ОВ и ВА имеет длину, большую чем L/3, необходимо чтобы наудачу поставленная точка B(x) попала в отрезок b, длина которого l=L/3. А т. к. вероятность
попадания точки на отрезок пропорциональна длине отрезка, и не зависит от его расположения на числовой оси, то искомую вероятность можно найти по формуле
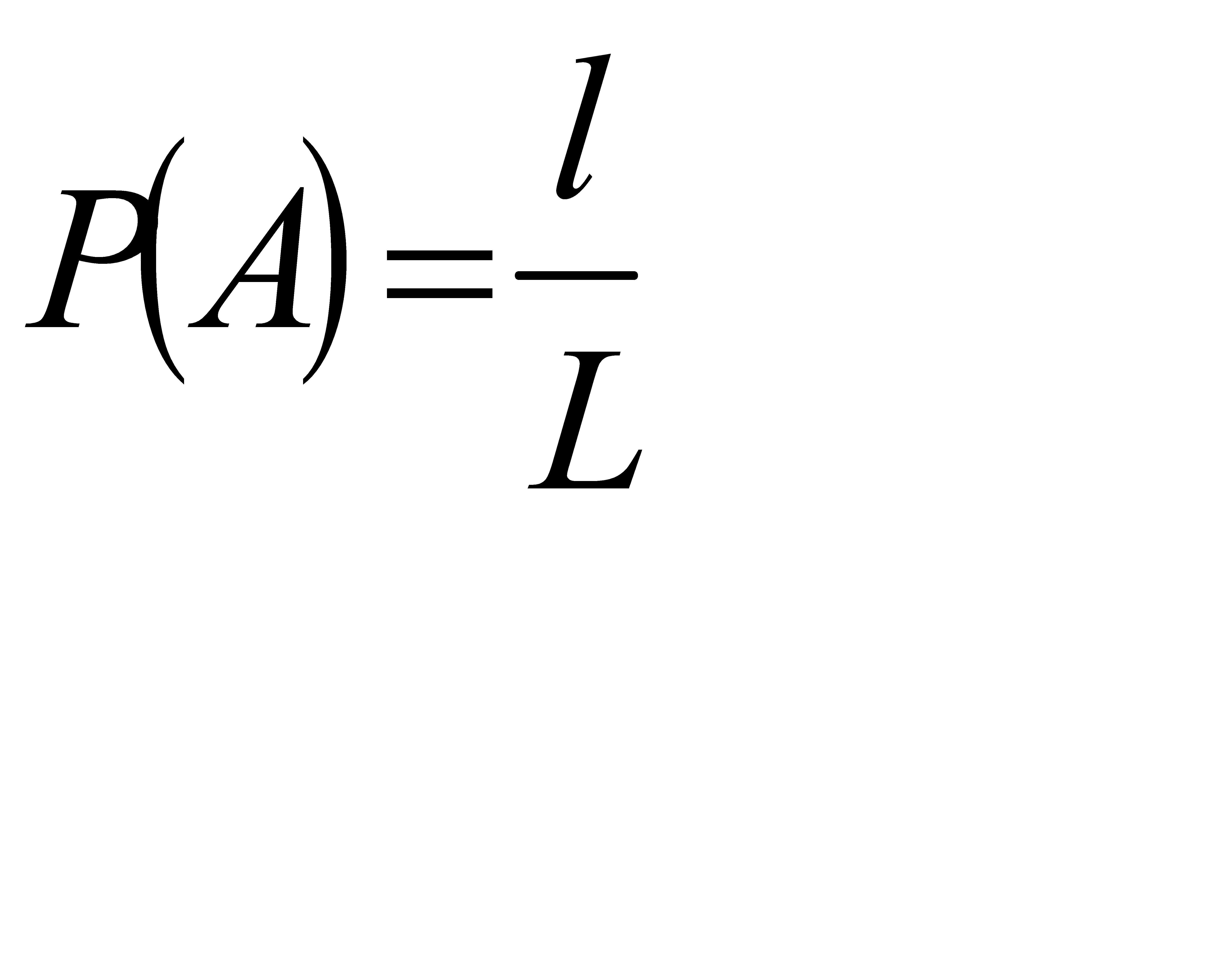
Подставляя наши значения (L=L; l=L/3) в данную формулу получаем искомую вероятность
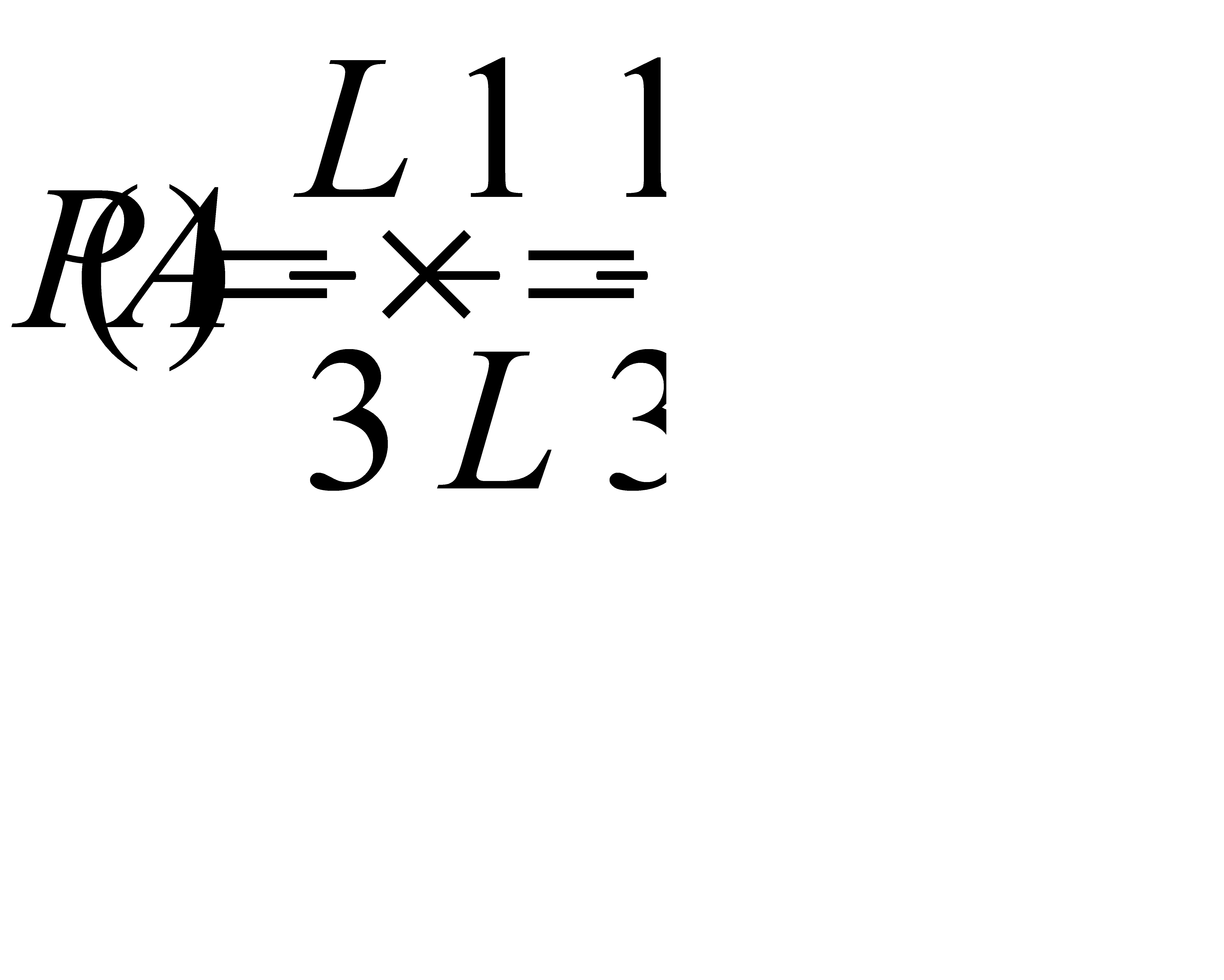
#28
Решение:
Т. к. вероятность попадания точки в круг пропорциональна площади круга, и не зависит от его расположения, то мы можем вычислить вероятность того, что точка наудачу брошенная в большой круг попадет также и в малый круг по формуле:
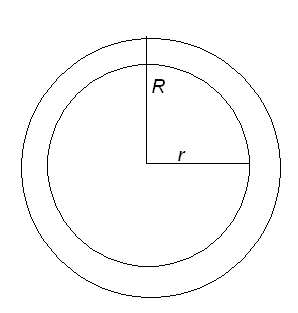
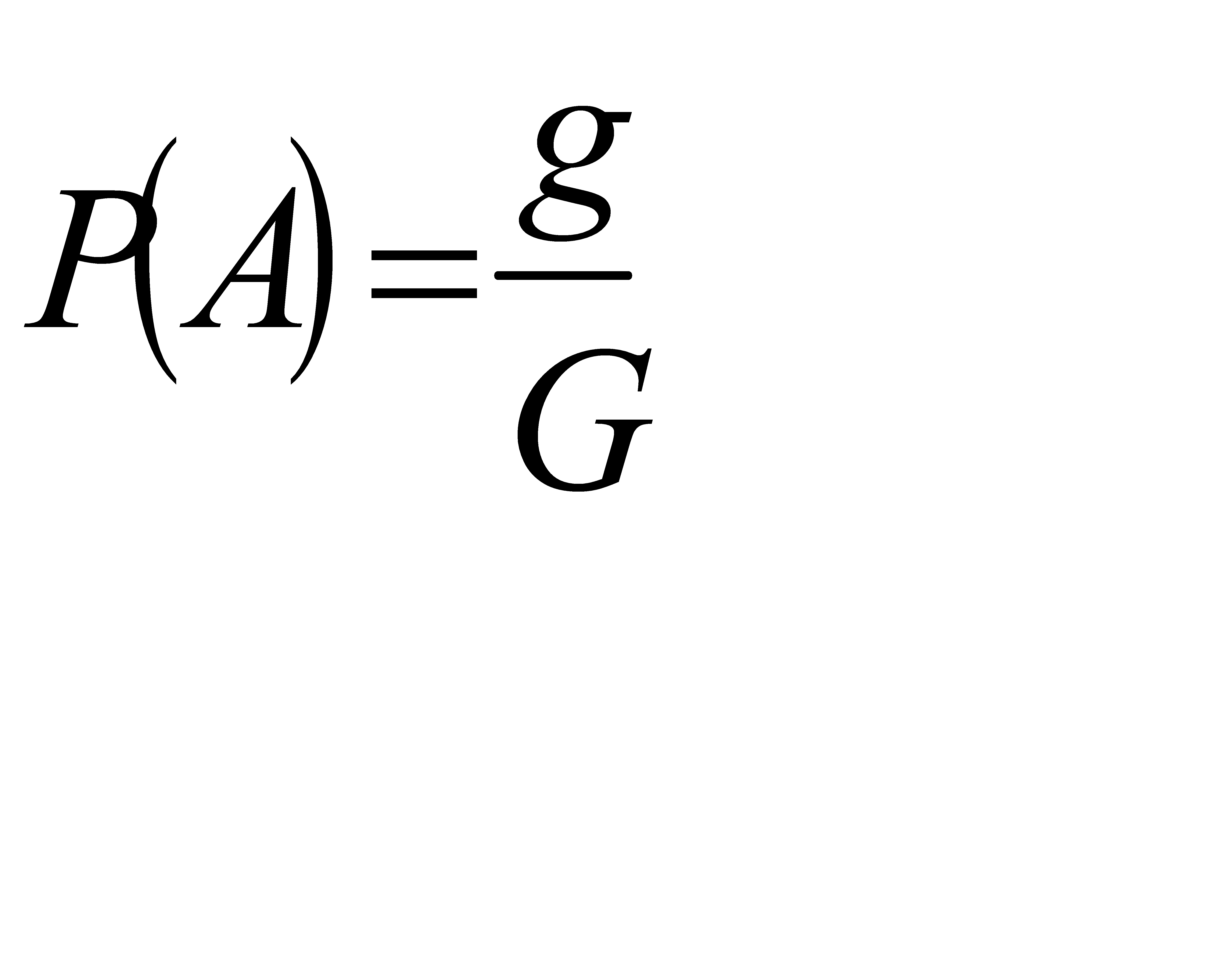 (*)
(*)
Где g-площадь малого круга, а G-площадь большого круга. Вычислим площади.
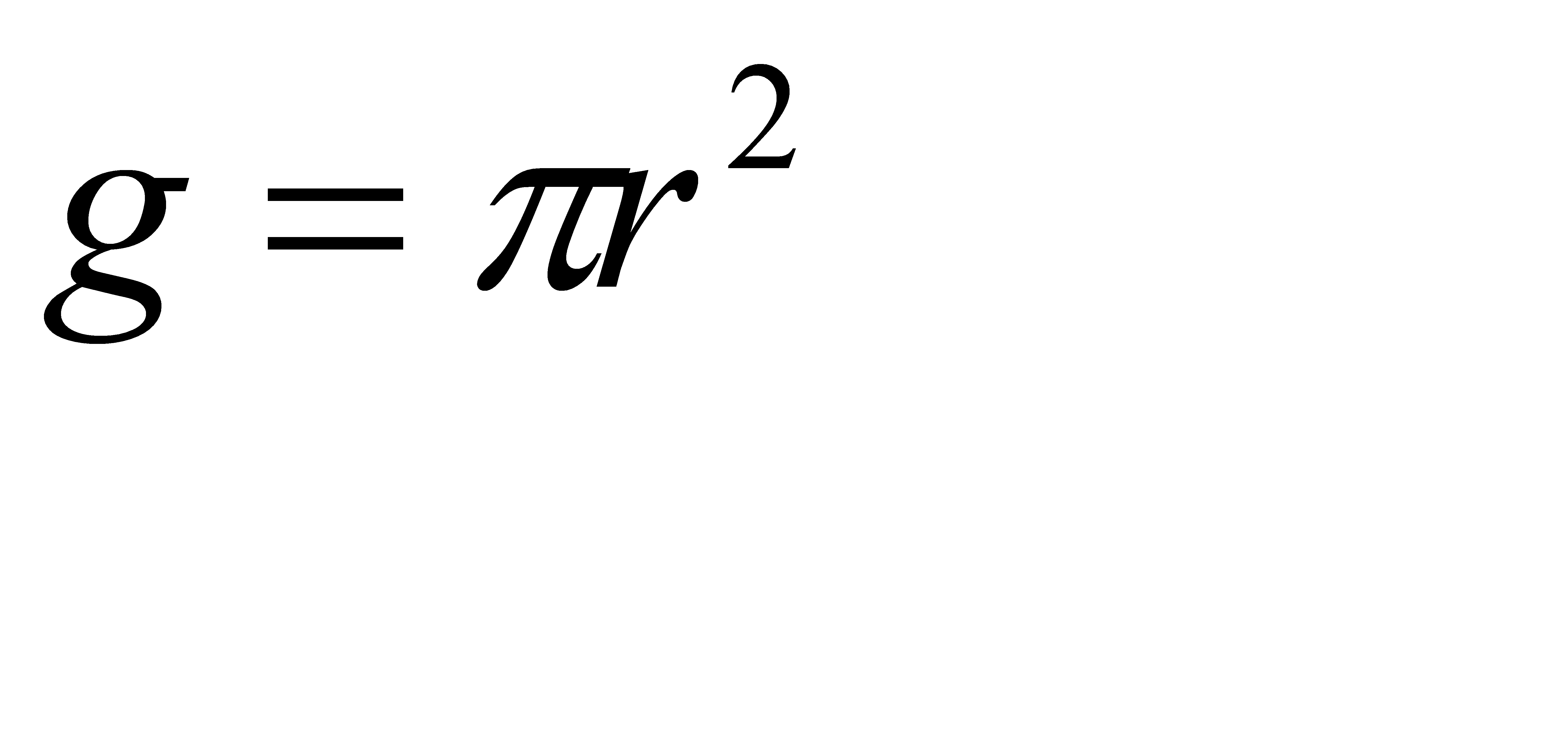

Подставив их в формулу (*) получим искомую вероятность

#29
Решение:
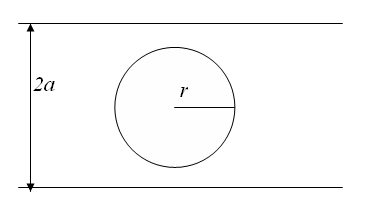 Для того чтобы монета не пересекла параллельные прямые, необходимо, чтобы при броске расстояние от монеты до прямых было равно
Для того чтобы монета не пересекла параллельные прямые, необходимо, чтобы при броске расстояние от монеты до прямых было равно
l=(2a-2r)
А общее расстояние, между двумя прямыми -
L=2a
Т. к. нам не важно куда приземлится монета, а главное чтоб она не пересекла прямые, то мы можем воспользоваться формулой 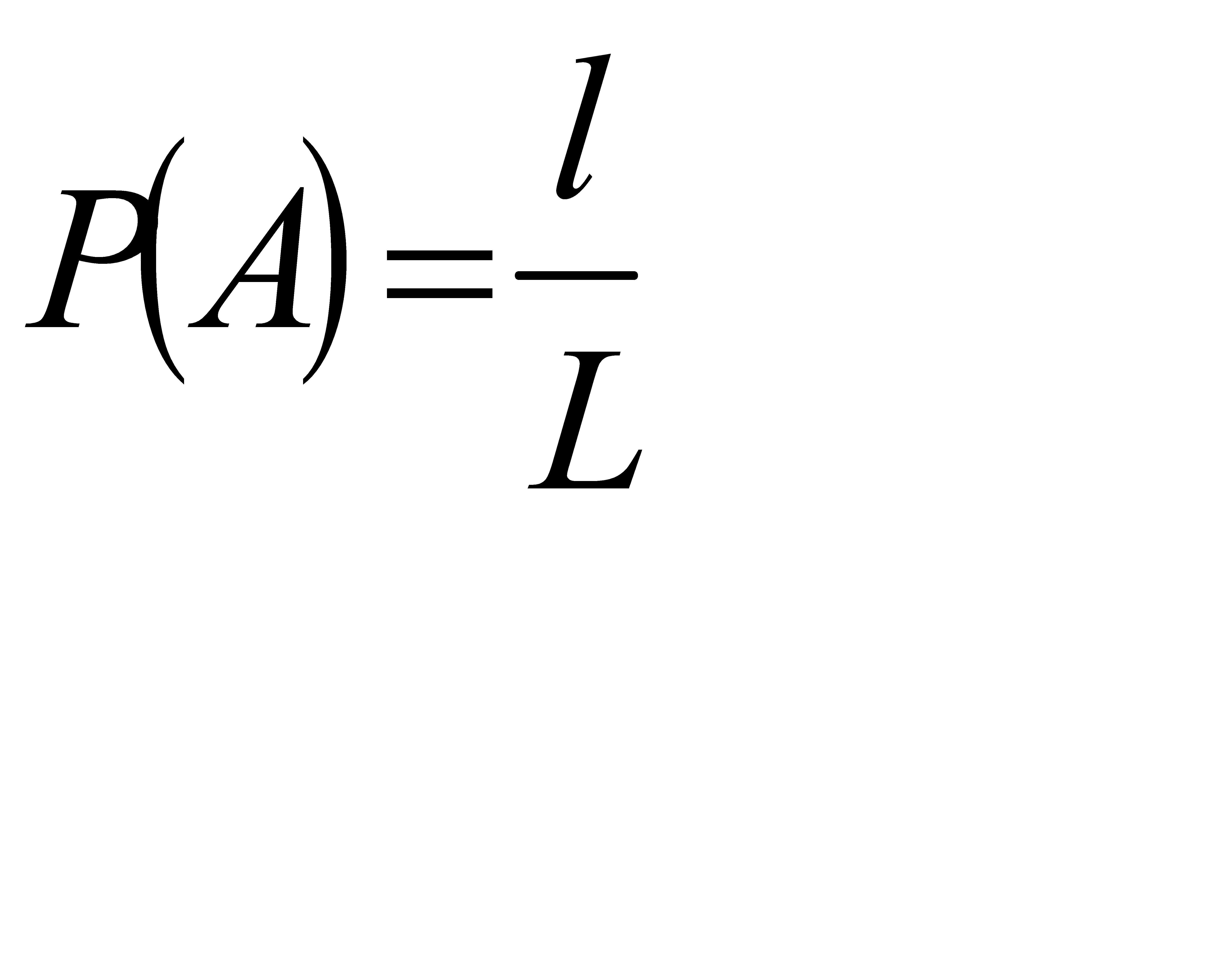 для нахождения вероятности того, что монета не пересечет ни одной из прямых.
для нахождения вероятности того, что монета не пересечет ни одной из прямых.
Тогда искомая вероятность равна 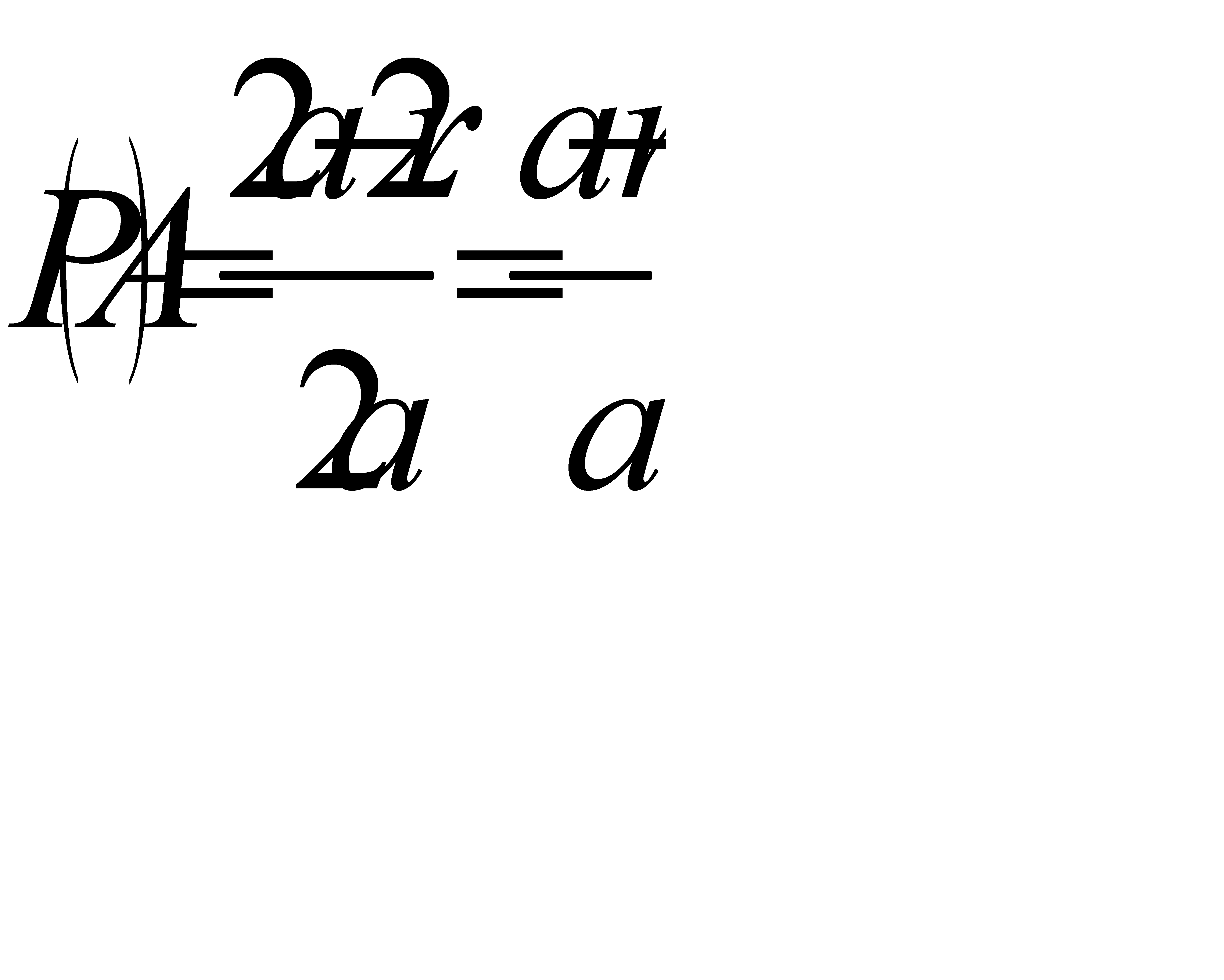
#30
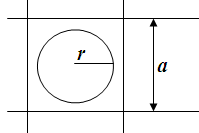 Решение:
Решение:
Событие А – монета не пересечёт ни одной из сторон квадрата можно представить в виде двух событий: В – монета не пересечёт вертикальных линий и С – монета не пересечёт горизонтальных линий. Тогда вероятность наступления события А можно представить в виде умножения вероятностей событий В и С.

Аналогично предыдущей задаче вычисляем вероятности событий В и С. Получаем что
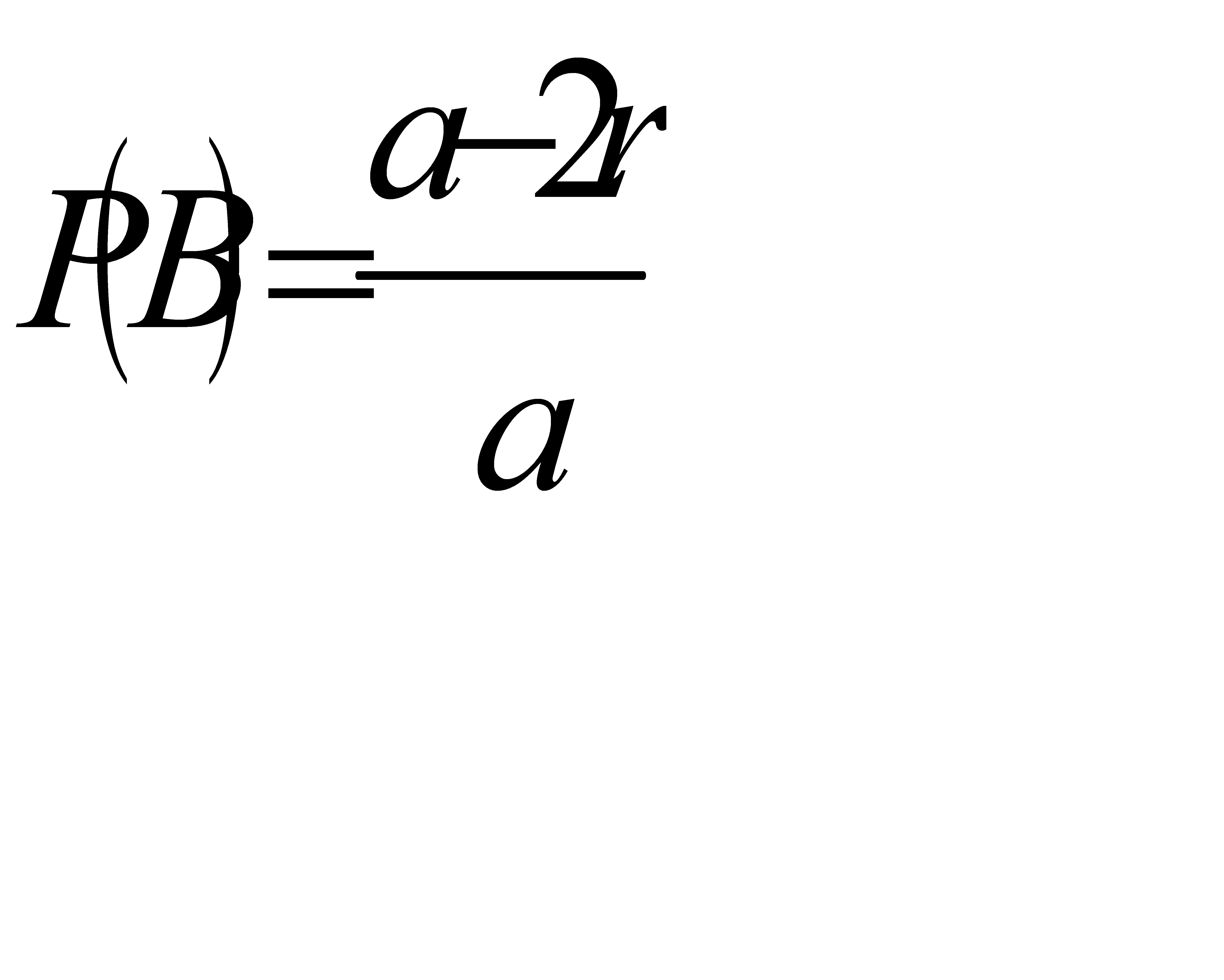 ;
; 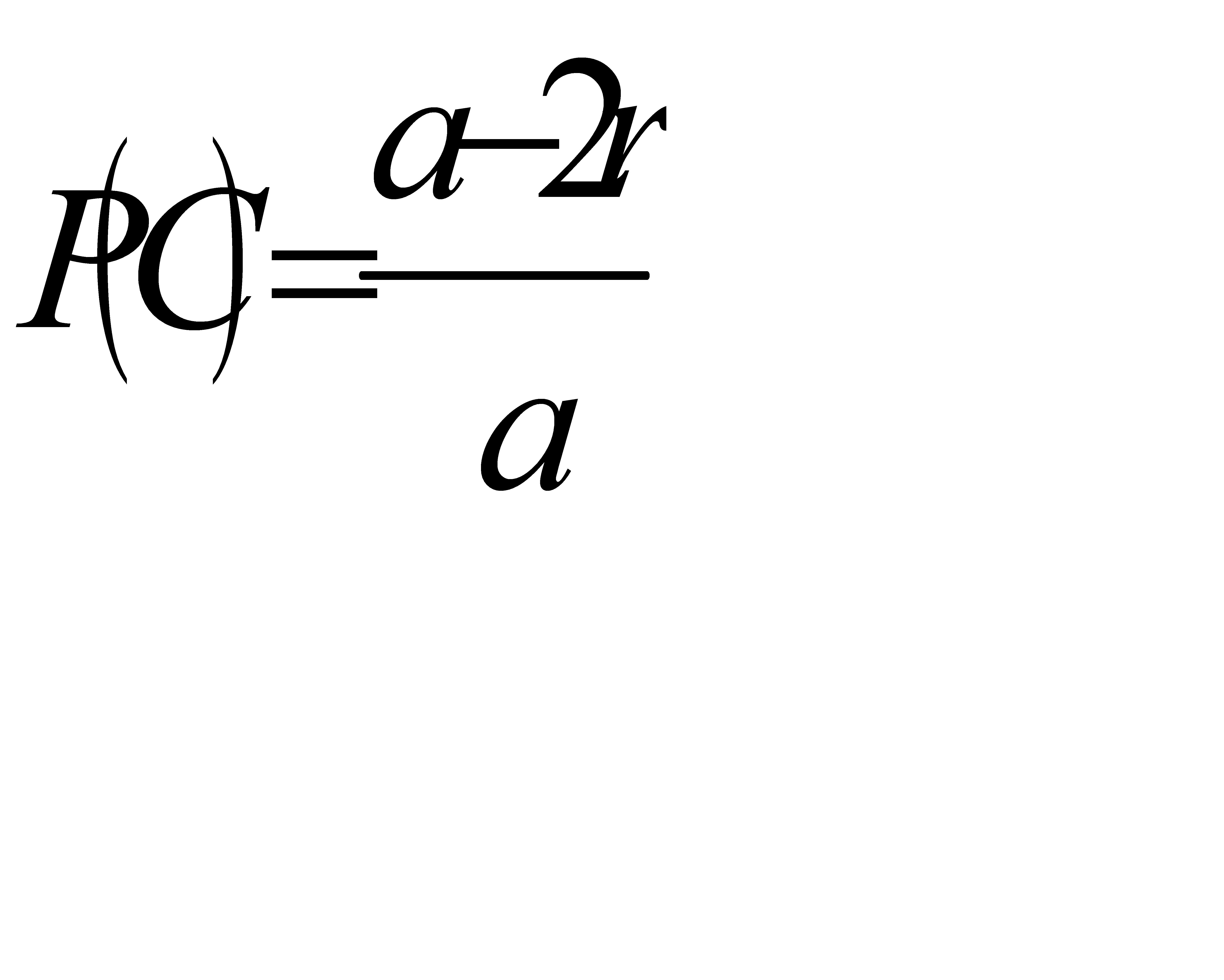
Тогда искомая вероятность равна 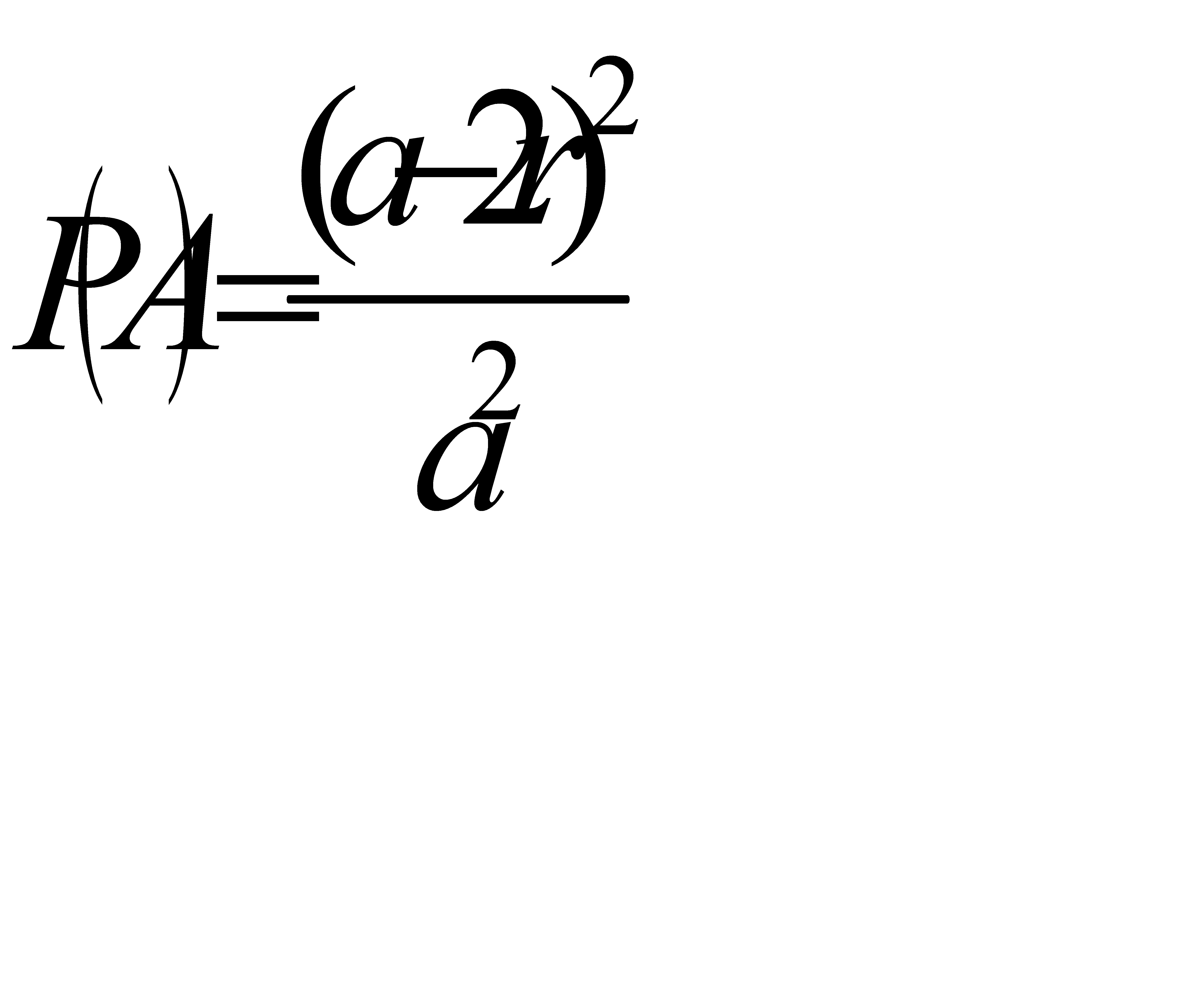
#31
Решение:
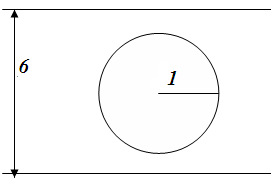 Данная задача является частным случаем задачи №29. Воспользуемся выведенной в ходе решения той задачи формулой, подставив в неё значения a=3; r=1:
Данная задача является частным случаем задачи №29. Воспользуемся выведенной в ходе решения той задачи формулой, подставив в неё значения a=3; r=1:
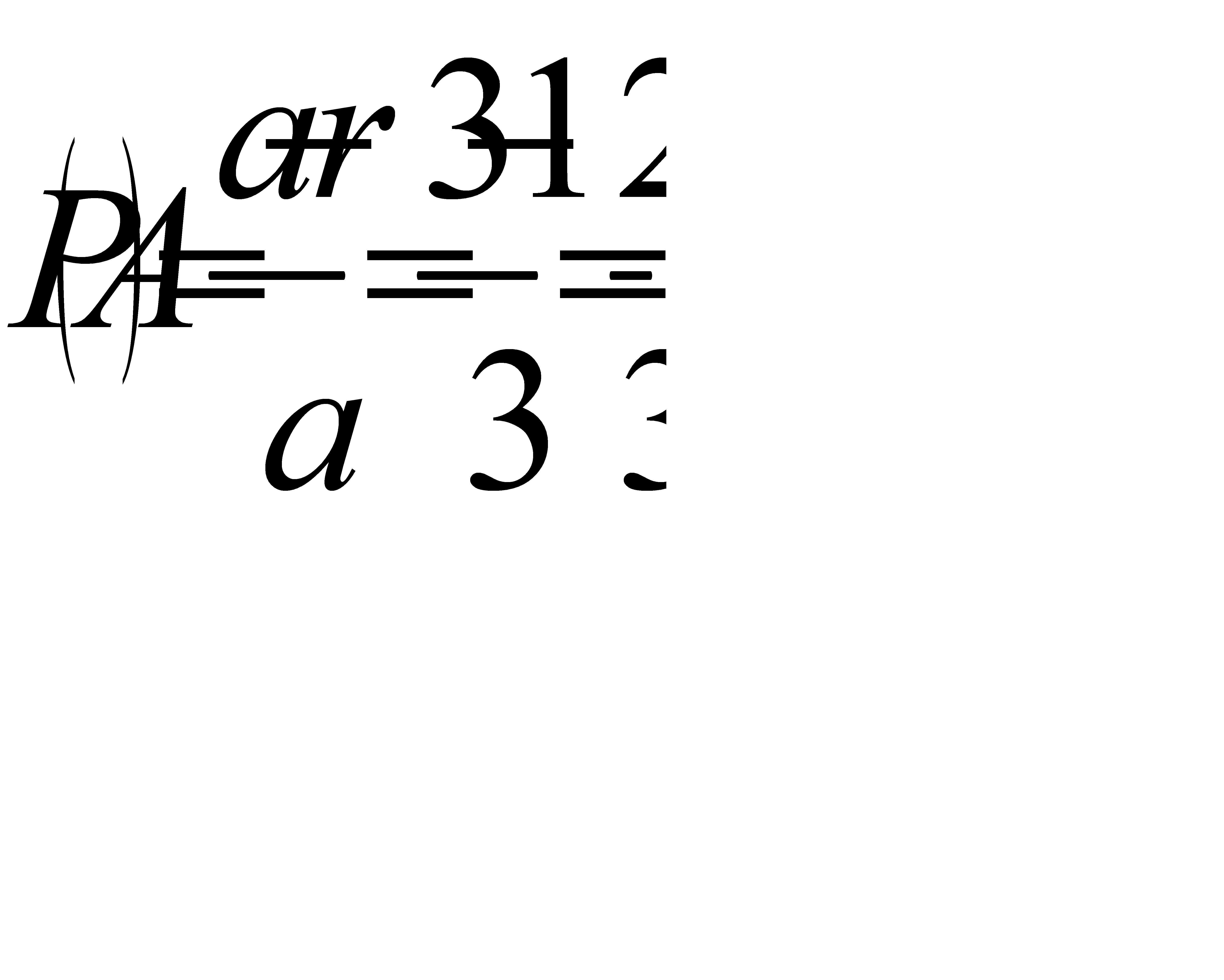
Ответ: вероятность того, что круг не пересечет ни одной из прямых равна 2/3.
#32
Решение:
Т. к. вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры, и не зависит от её расположения, то мы можем вычислить вероятность того, что точка наудачу брошенная в большой круг попадет также и в кольцо, образованное построенными окружностями по формуле:
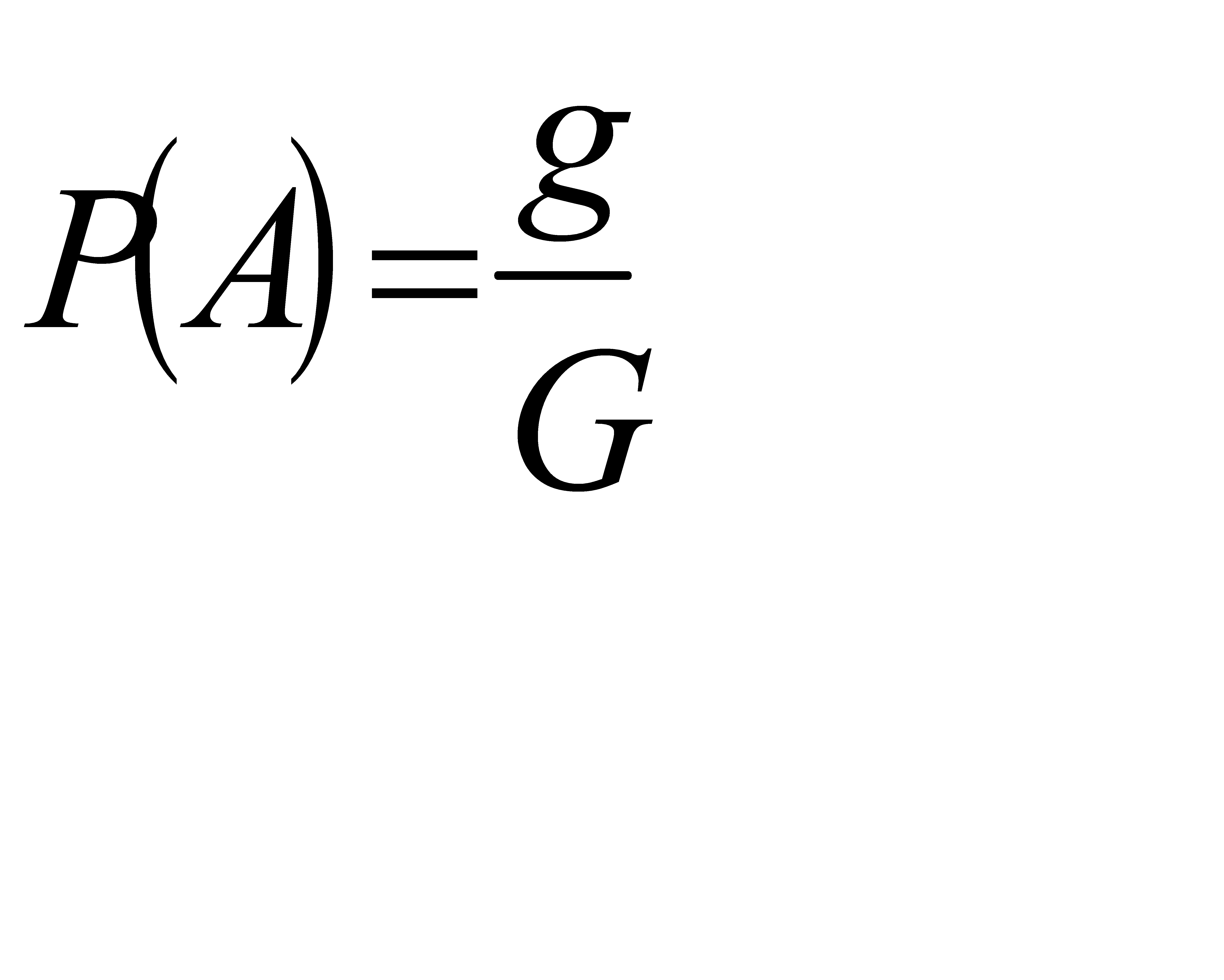
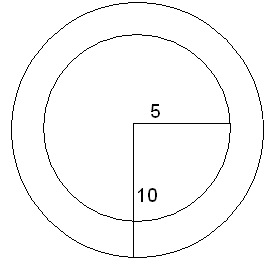 Где g-площадь кольца, а G-площадь большого круга. Вычислим площади. Пусть R – радиус большой окружности, а r – радиус малой окружности.
Где g-площадь кольца, а G-площадь большого круга. Вычислим площади. Пусть R – радиус большой окружности, а r – радиус малой окружности.

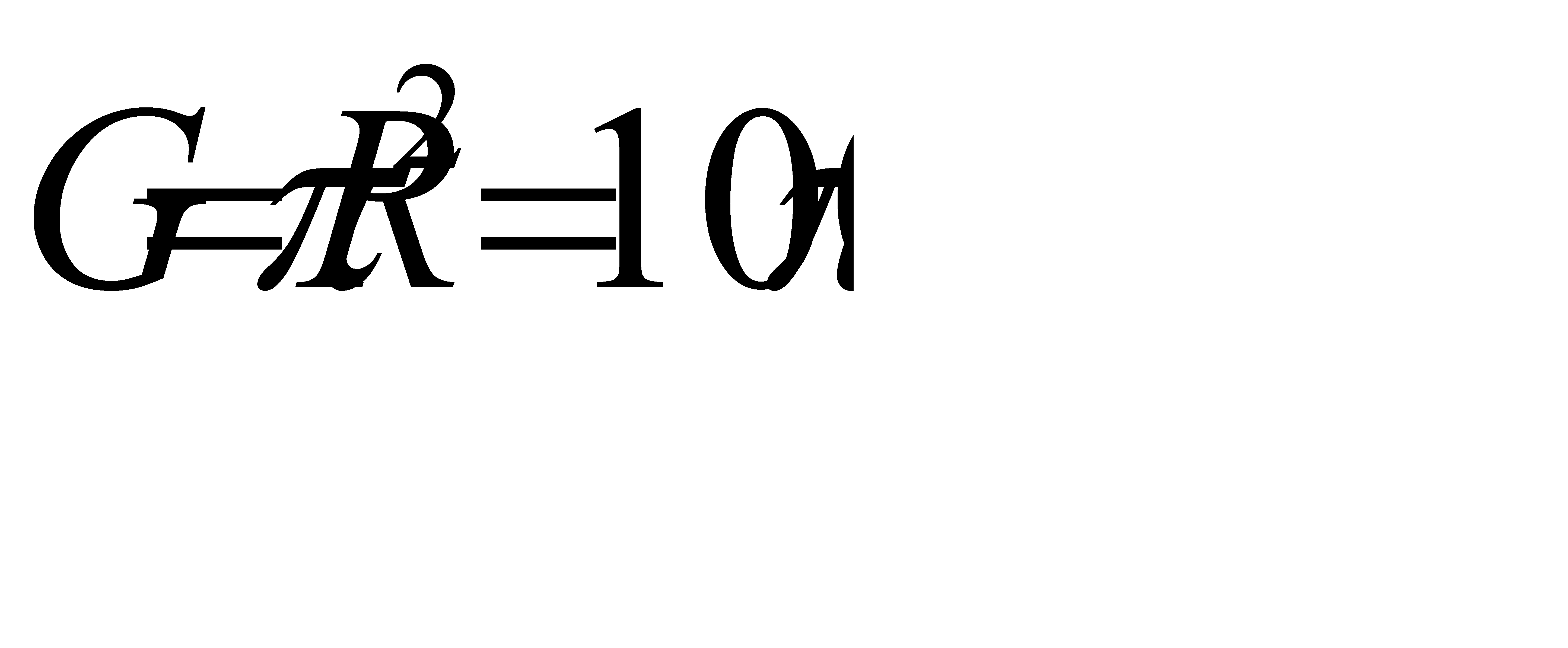
Тогда искомая вероятность равна
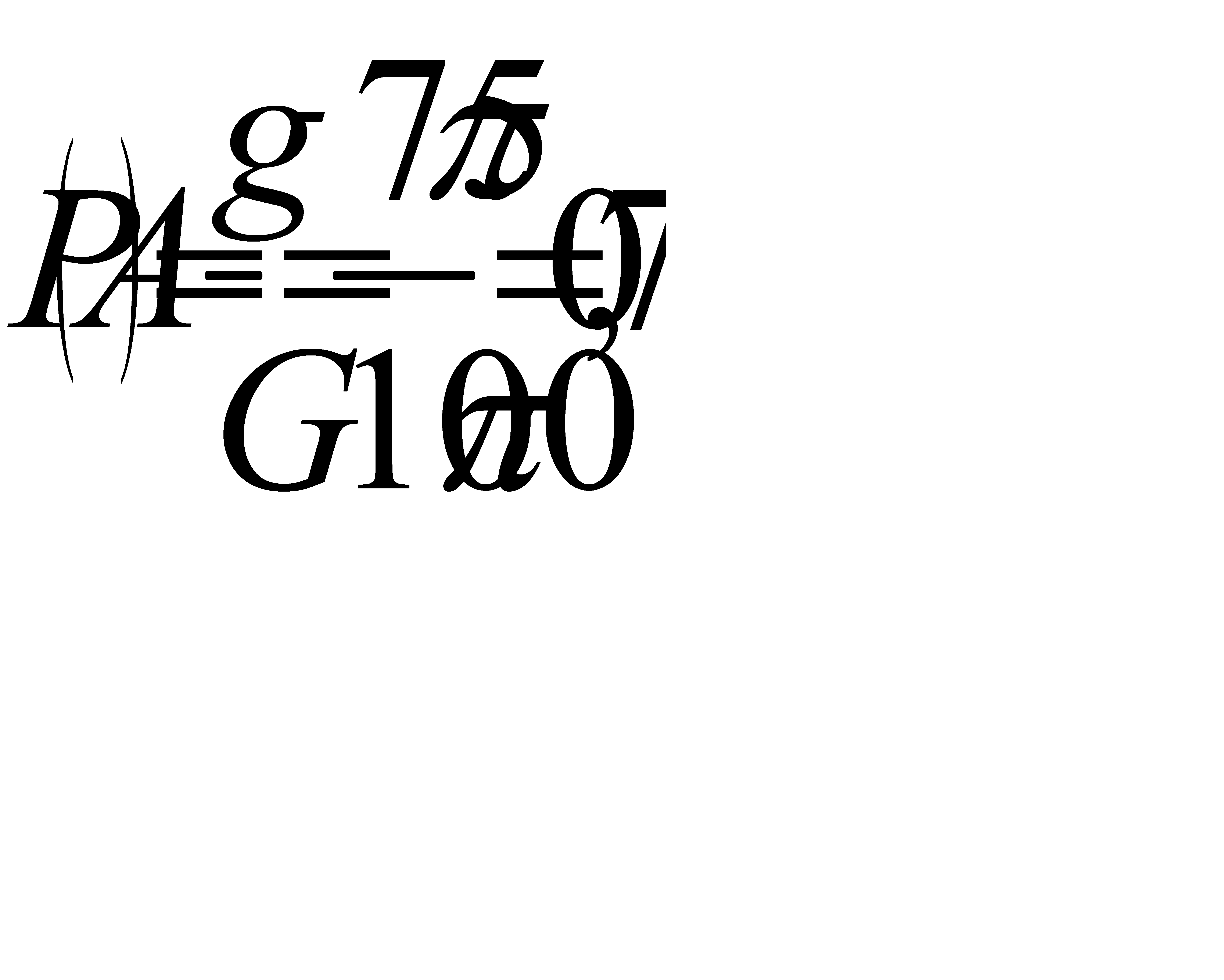
#33
Решение:
А)
B Рассмотрим треугольник АВС. Он является равнобедренным, так как АС=АВ=R. По формуле
А площади любого треугольника, найдем его площадь:
C 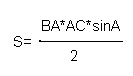 По свойствам квадрата угол
По свойствам квадрата угол
ВАС=90. Следовательно, мы получим:
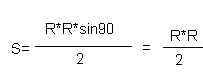 Но так как квадрат составляют 4 таких треугольника, то площадь квадрата
Но так как квадрат составляют 4 таких треугольника, то площадь квадрата
Sкв. =4S=2*R*R. Площадь круга Sкр=п*R*R
Из условия задачи, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга, следует:
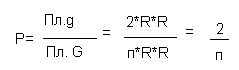
Б) В
По теореме синусов 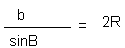
Так как треугольник
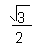 АВС равносторонний, следовательно, все его
АВС равносторонний, следовательно, все его
углы равны 60 градусам. Из данной формулы найдем сторону треугольника, которая a=b=c.
Так как sin60= , то получим, что b= 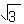 *R.
*R.
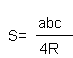 Существует формула площади треугольника, вписанного в окружность
Существует формула площади треугольника, вписанного в окружность
Отсюда, мы получим, что площадь треугольника равна 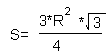 .
.
Из условия задачи, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга, следует:
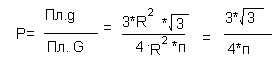
Ответ: А)2/п Б) 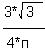
#34
Площадь круга Sкр=п*R*R. Так как диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет, то белый занимает половину круга, а остальную половину круга занимает черный цвет. Следовательно, 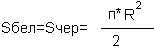
А так как вероятность попадания пули в плоскую фигуру пропорциональна площади этой фигуры, то
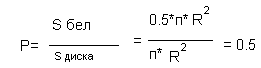
Ответ: ½
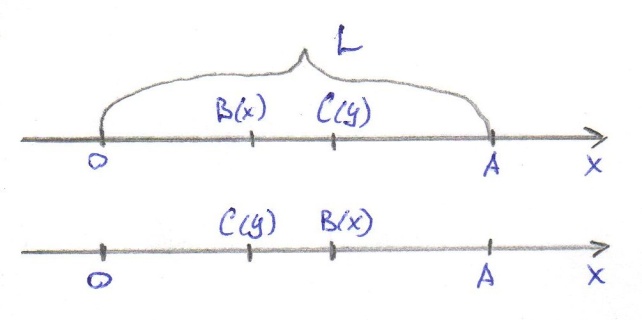
#35
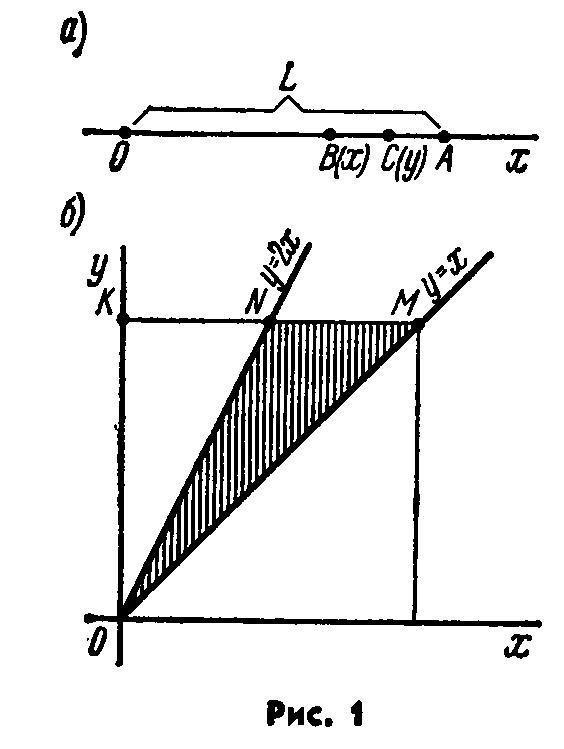 Решение: Координаты точек В и С должны удовлетворять неравенствам
Решение: Координаты точек В и С должны удовлетворять неравенствам  Введём в рассмотрение прямоугольную систему координат xOy. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей прямоугольному треугольнику OKM (рис 1, б). Таким образом, этот треугольник можно рассматривать как фигуру G, координаты точек которой представляют соответственно все возможные значения координат точек В и С.
Введём в рассмотрение прямоугольную систему координат xOy. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей прямоугольному треугольнику OKM (рис 1, б). Таким образом, этот треугольник можно рассматривать как фигуру G, координаты точек которой представляют соответственно все возможные значения координат точек В и С.
Длина отрезка ВС должна быть меньше длины отрезка ОВ, т. е. должно иметь место неравенство 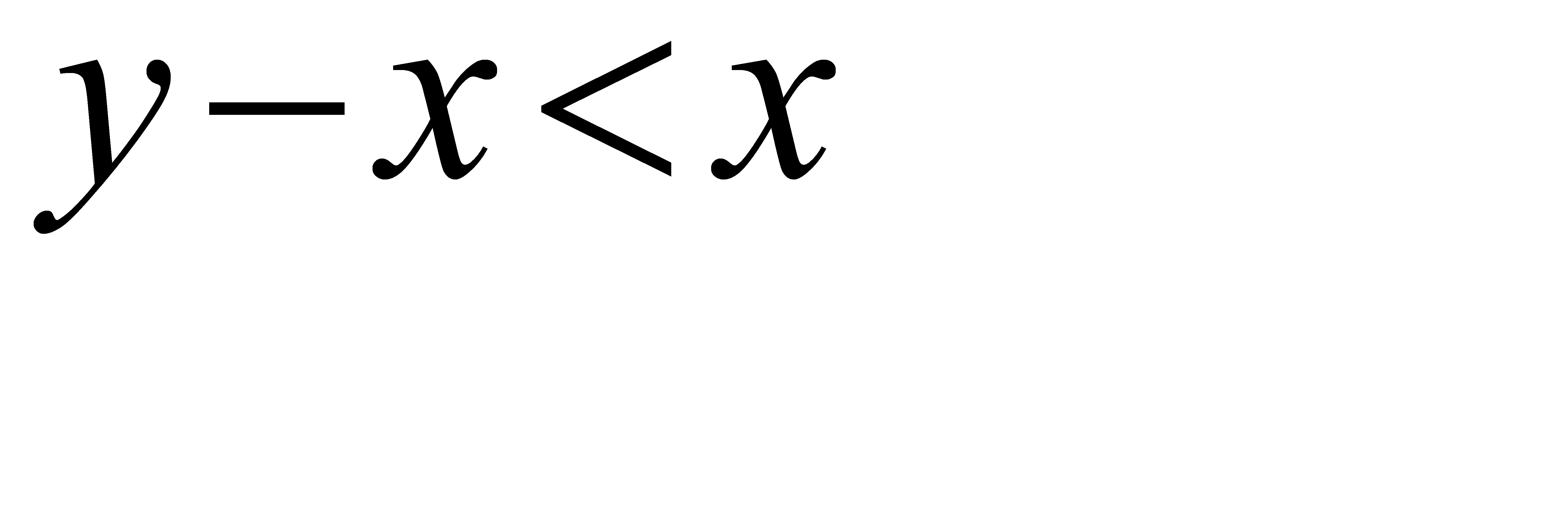 , или
, или 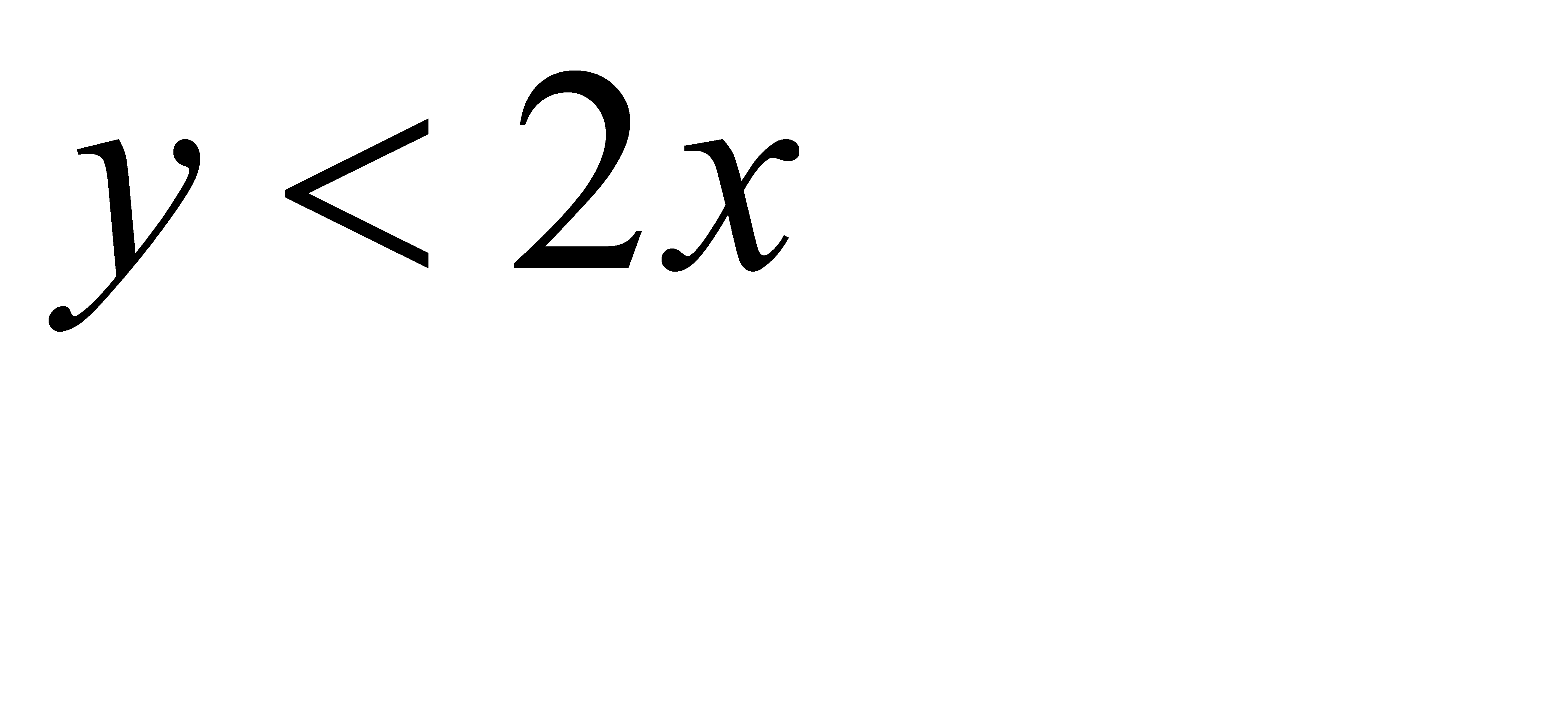 . Последнее неравенство выполняется для координат тех точек фигуры G (прямоугольного треугольника OKM), которые лежат ниже прямой
. Последнее неравенство выполняется для координат тех точек фигуры G (прямоугольного треугольника OKM), которые лежат ниже прямой 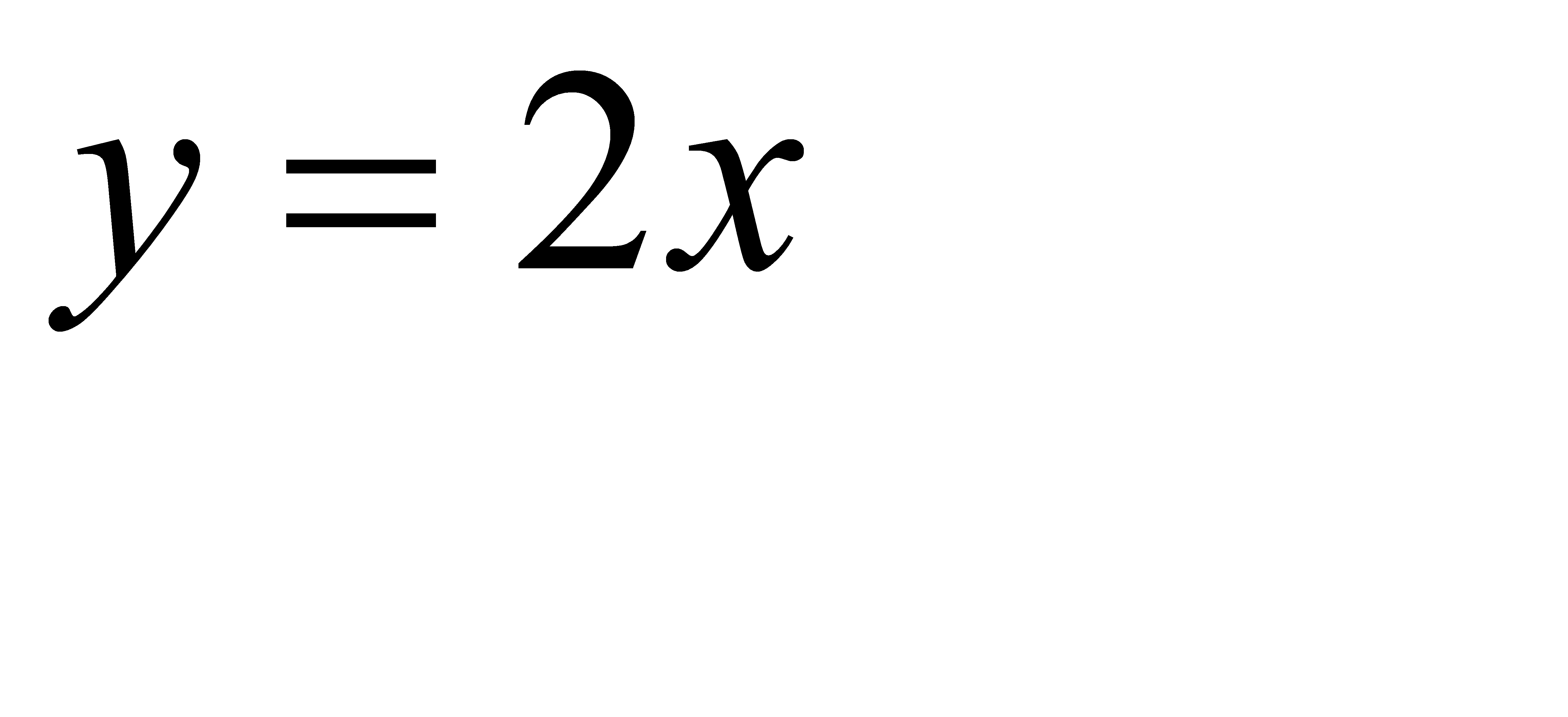 (прямая ON). Как видно из рис. 1, б, все эти точки принадлежат заштрихованному треугольнику ONM. Таким образом, этот треугольник можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими интересующему нас событию (длина отрезка ВС меньше длины отрезка ОВ).
(прямая ON). Как видно из рис. 1, б, все эти точки принадлежат заштрихованному треугольнику ONM. Таким образом, этот треугольник можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими интересующему нас событию (длина отрезка ВС меньше длины отрезка ОВ).
Искомая вероятность

#36
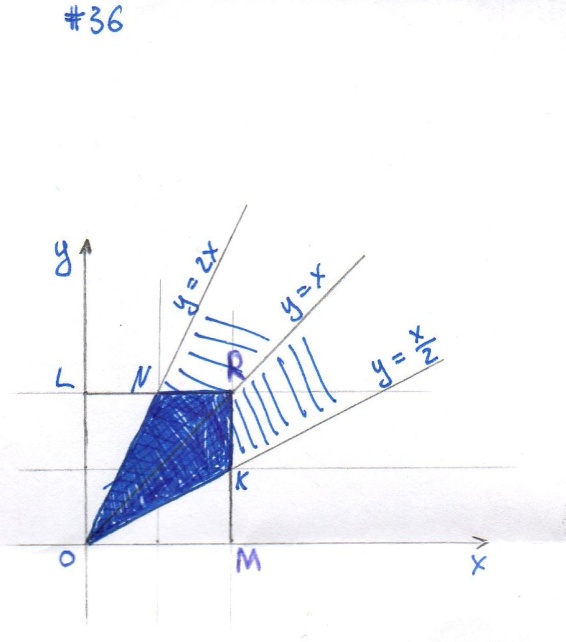
Решение: Координаты точек В и С должны удовлетворять неравенствам
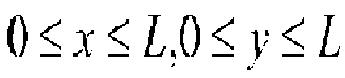
Введём в рассмотрение прямоугольную систему координат xOy. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату OLRM. Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют соответственно все возможные значения координат точек В и С.
Возможны два случая:
1)B< C
Длина отрезка ВС должна быть меньше длины отрезка ОВ, т. е. должно иметь место неравенство 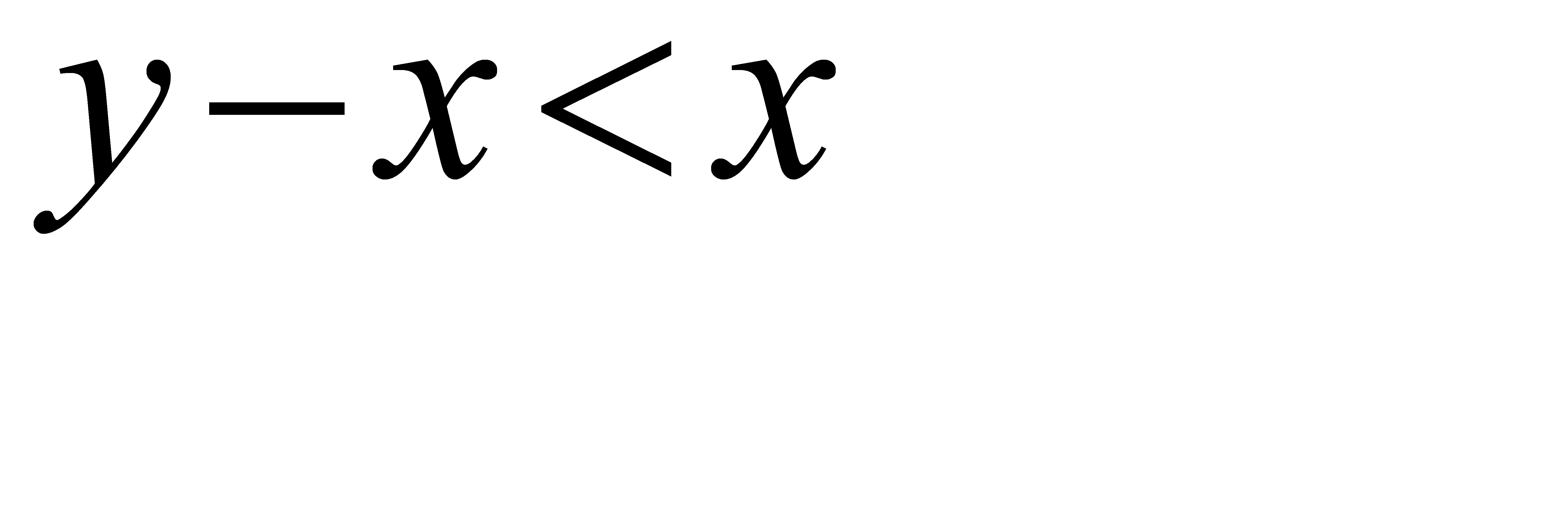 , или
, или 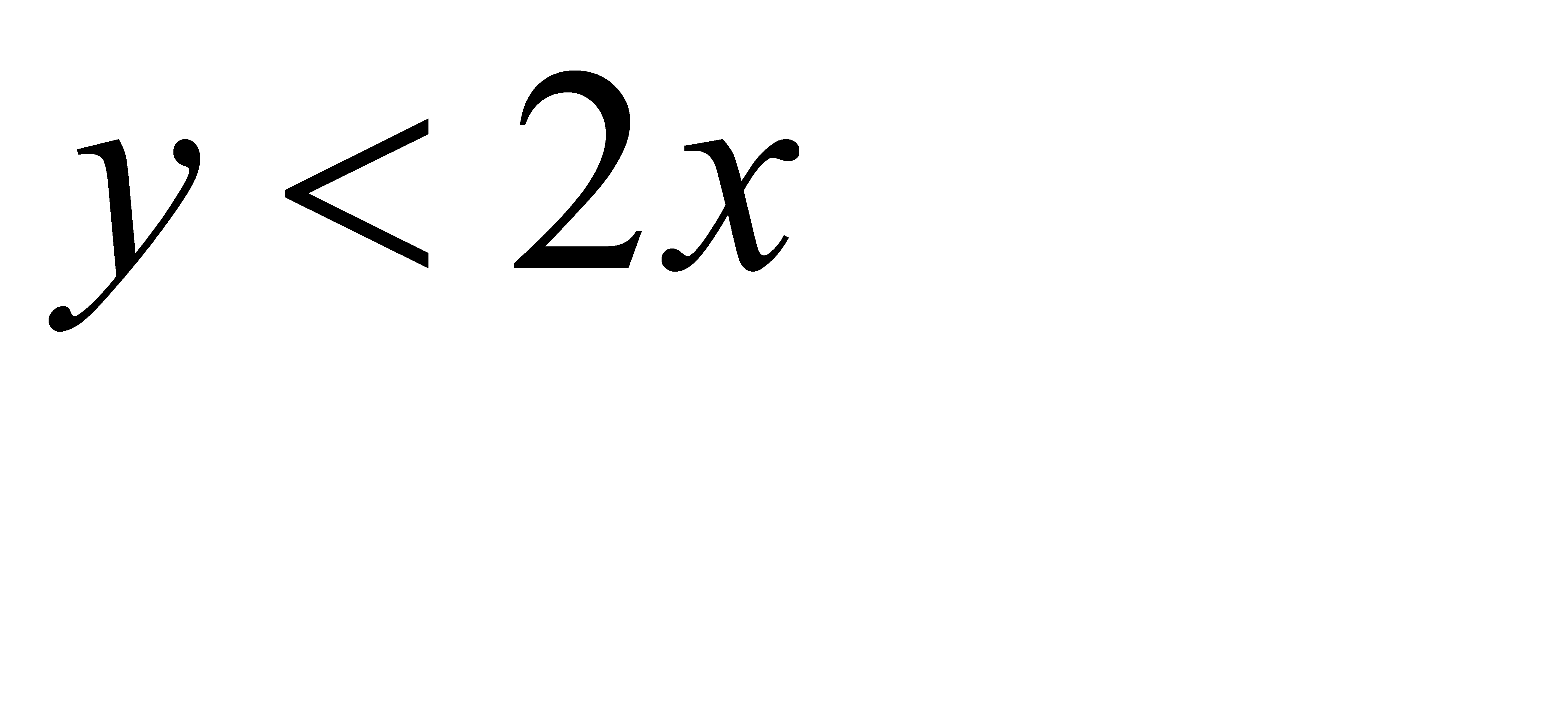 . Последнее неравенство выполняется для координат тех точек фигуры G, которые лежат ниже прямой
. Последнее неравенство выполняется для координат тех точек фигуры G, которые лежат ниже прямой 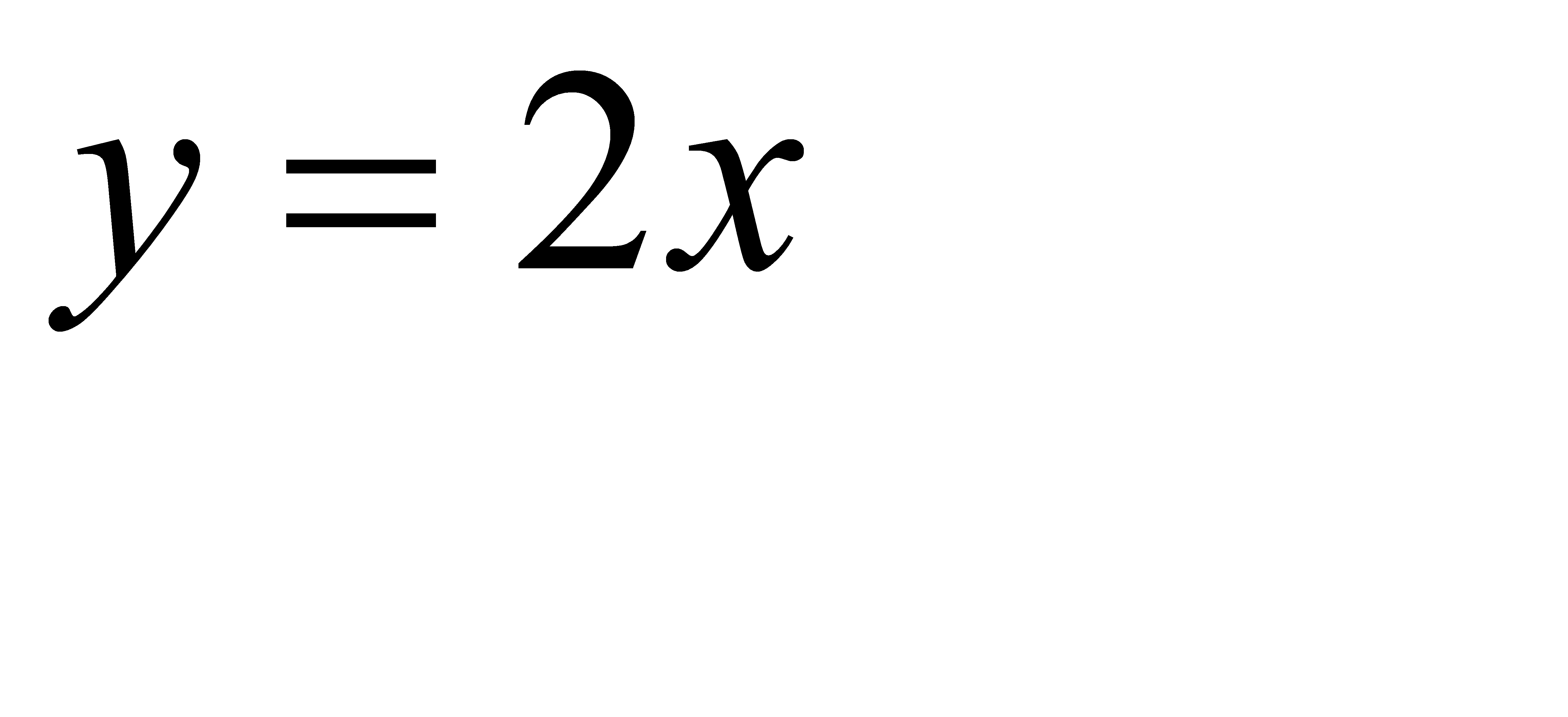 (прямая ON). Как видно из рисунка, все эти точки принадлежат заштрихованному треугольнику ONR.
(прямая ON). Как видно из рисунка, все эти точки принадлежат заштрихованному треугольнику ONR.
2)B> =C
Аналогичное утверждение. Должны одновременно выполняться 2 условия: y< =x, y> x/2.
Как видно из рисунка, все эти точки принадлежат заштрихованному треугольнику ORK.
Таким образом, фигуру ONRK можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими интересующему нас событию.
Искомая вероятность

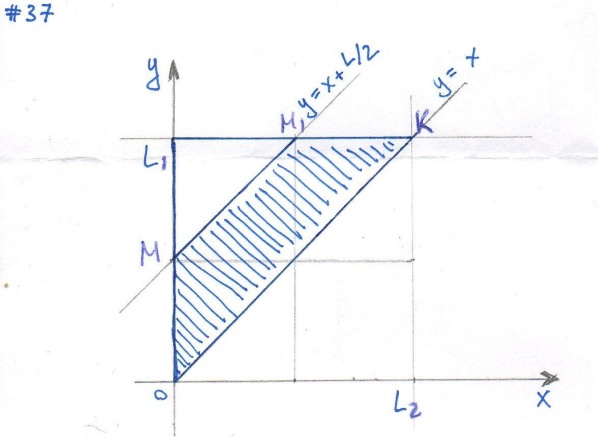
#37
Решение: Координаты точек В и С должны удовлетворять неравенствам 
Введём в рассмотрение прямоугольную систему координат xOy. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей прямоугольному треугольнику OL1 K. Таким образом, этот треугольник можно рассматривать как фигуру G, координаты точек которой представляют соответственно все возможные значения координат точек В и С.
Длина отрезка BC должна оказаться меньше L/2, т. е имеет место неравенство:
y< x+L/2.
Последнее неравенство выполняется для точек фигуры OMM1K( см. рисунок). Таким образом, эту фигуру можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими интересующему нас событию.
Искомая вероятность
#38
.
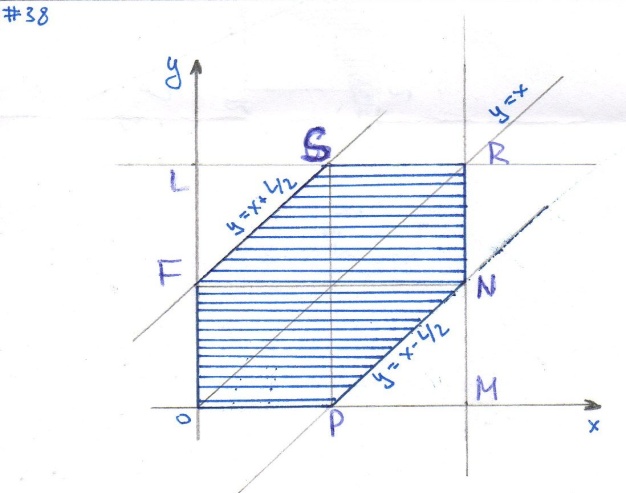
Решение: Координаты точек В и С должны удовлетворять неравенствам
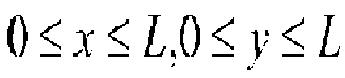
Введём в рассмотрение прямоугольную систему координат xOy. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату OLRM. Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют соответственно все возможные значения координат точек В и С.
Возможны 2 случая:
1)B< C Длина отрезка ВС должна быть меньше L/2, т. е имеет место неравенство
y< x+L/2.
2)B> =C. Имеет место неравенство .
Эти условия выполняются для фигуры OFSRNP( см. рисунок). Таким образом, эту фигуру можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими интересующему нас событию.
Искомая вероятность
#39
Задача Бюффона (французский естествоиспытатель XVIII в. ). плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2a. На плоскость наудачу бросают иглу длины 2l (l< a). Найти вероятность того, что игла пересечет какую-нибудь прямую.
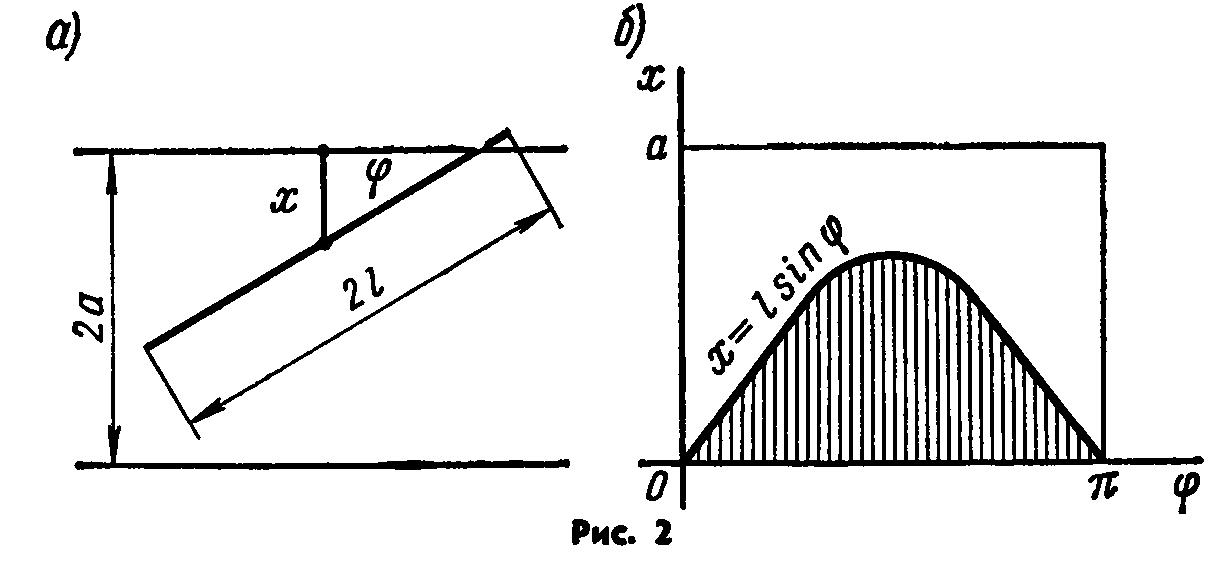
Решение. Введём следующие обозначения: х-расстояние от середины иглы до ближайшей параллели;  -угол, составленный иглой с этой параллелью (рис. 2, а).
-угол, составленный иглой с этой параллелью (рис. 2, а).
Положение иглы полностью определяется заданием определённых значений х и  , причём х принимает значения от 0 до а; возможные значения
, причём х принимает значения от 0 до а; возможные значения  изменяются от 0 до
изменяются от 0 до  . Другими словами, середина иглы может попасть в любую из точек прямоугольника со сторонами а и
. Другими словами, середина иглы может попасть в любую из точек прямоугольника со сторонами а и  (рис. 2, б). Таким образом, этот прямоугольник можно рассматривать как фигуру G, точки которой представляют собой все возможные положения середины иглы. Очевидно, площадь фигуры G равна
(рис. 2, б). Таким образом, этот прямоугольник можно рассматривать как фигуру G, точки которой представляют собой все возможные положения середины иглы. Очевидно, площадь фигуры G равна  .
.
Найдём теперь фигуру g, каждая точка которой благоприятствует интересующему нас событию, т. е. каждая точка этой фигуры может служить серединой иглы, котрая пересекает ближайшую к ней параллель. Как видно из рис. 2, а, игла пересечёт ближайшую к ней параллель при условии 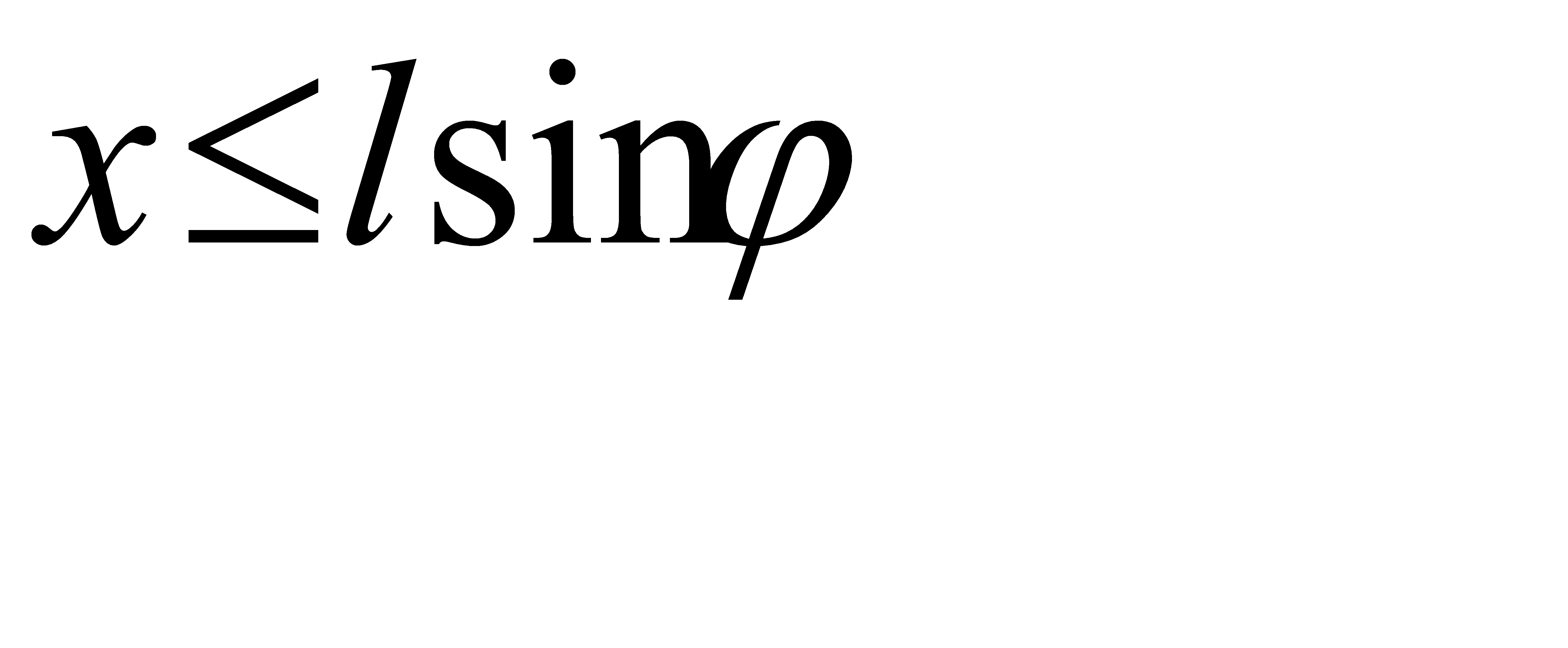 , т. е. если середина иглы попадёт в любую из точек фигуры, заштрихованной на рис. 2, б.
, т. е. если середина иглы попадёт в любую из точек фигуры, заштрихованной на рис. 2, б.
Таким образом, заштрихованную фигуру можно рассматривать как фигуру g. Найдём площадь этой фигуры:

Искомая вероятность того, что игла пересечёт прямую
 .
.
#40
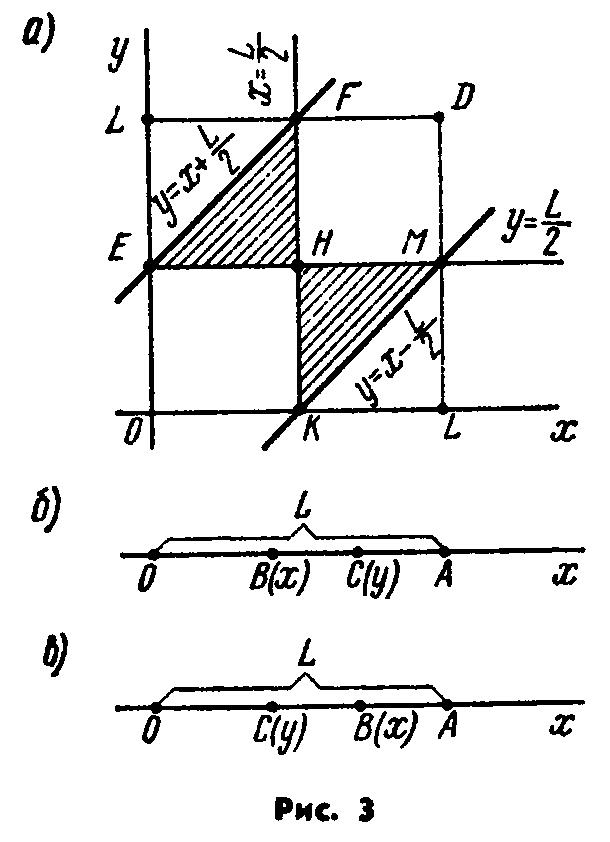
Решение: Для того, чтобы из трёх отрезков можно было построить треугольник, каждый из отрезков должен быть меньше суммы двух других. Сумма всех трёх отрезков равна L, поэтому каждый из отрезков должен быть меньше L/2.
Введём в рассмотрение прямоугольную систему координат xOy. Координаты любых двух точек В и С должны удовлетворять двойным неравенствам: 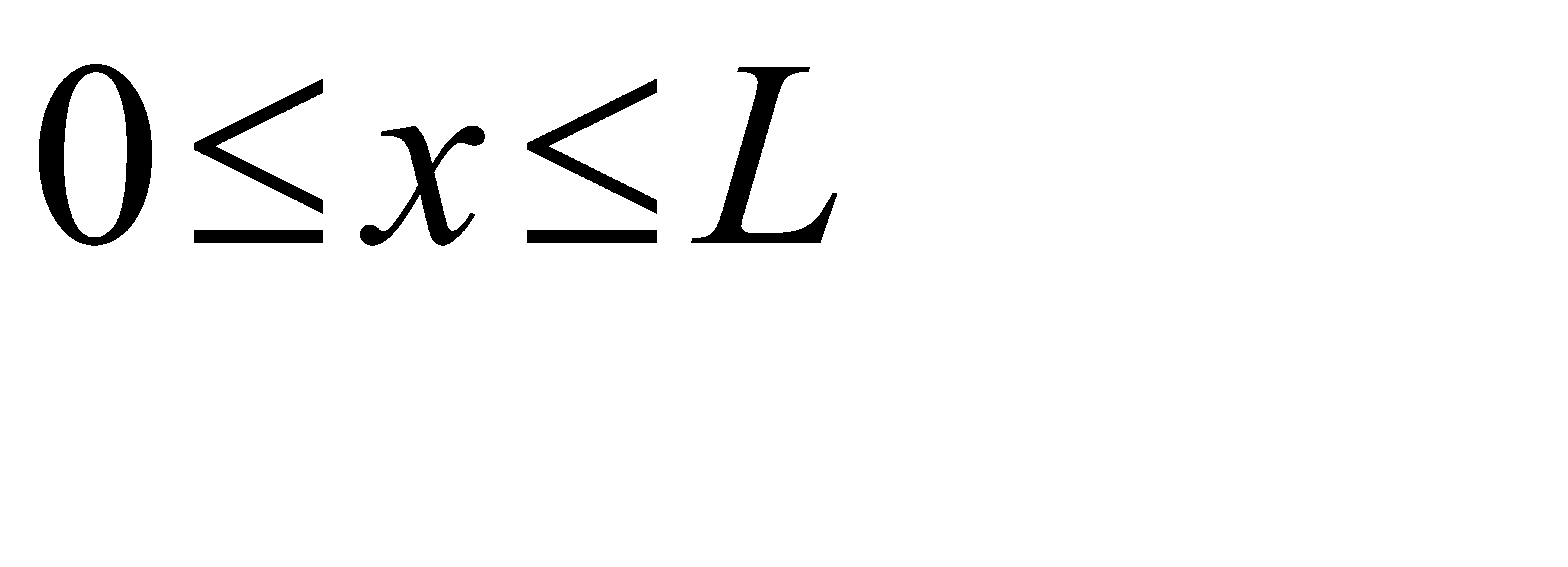
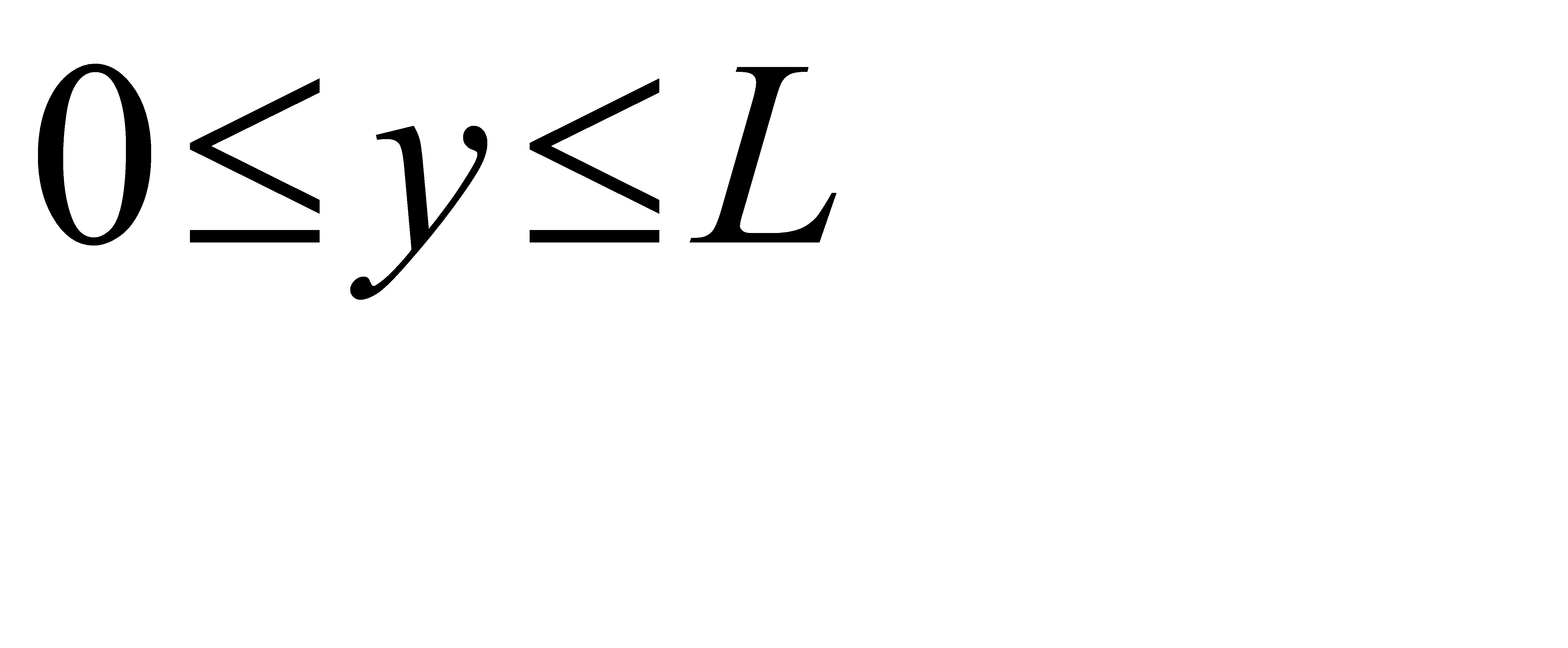 . Этим неравенствам удовлетворяют координаты любой точки М(x, y), принадлежащей квадрату OLDL (рис. 3, а). Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют все возможные значения координат точек В и С.
. Этим неравенствам удовлетворяют координаты любой точки М(x, y), принадлежащей квадрату OLDL (рис. 3, а). Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют все возможные значения координат точек В и С.
1. пусть точка С расположена правее точки В (рис. 3, б). Как указано выше, длины отрезков ОВ, ВС, СА должны быть меньше L/2, т. е. должны иметь место неравенства 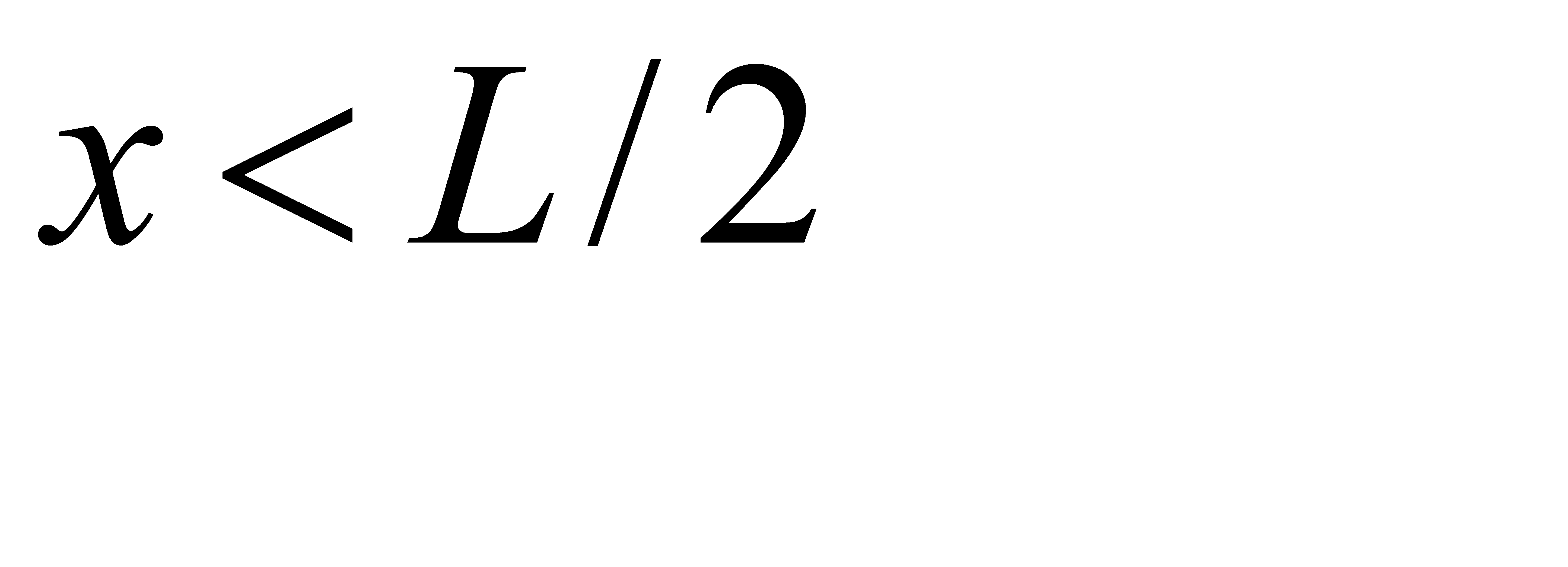 ,
, 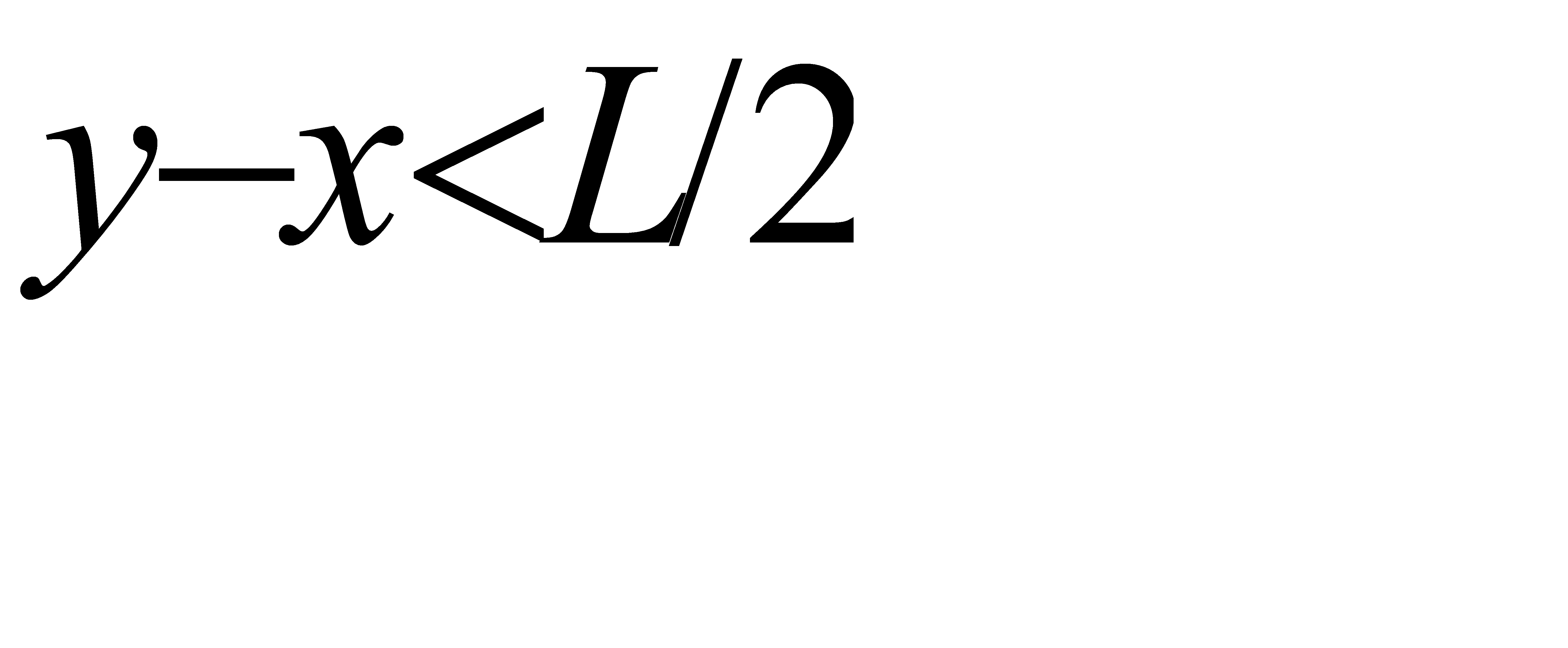 ,
, 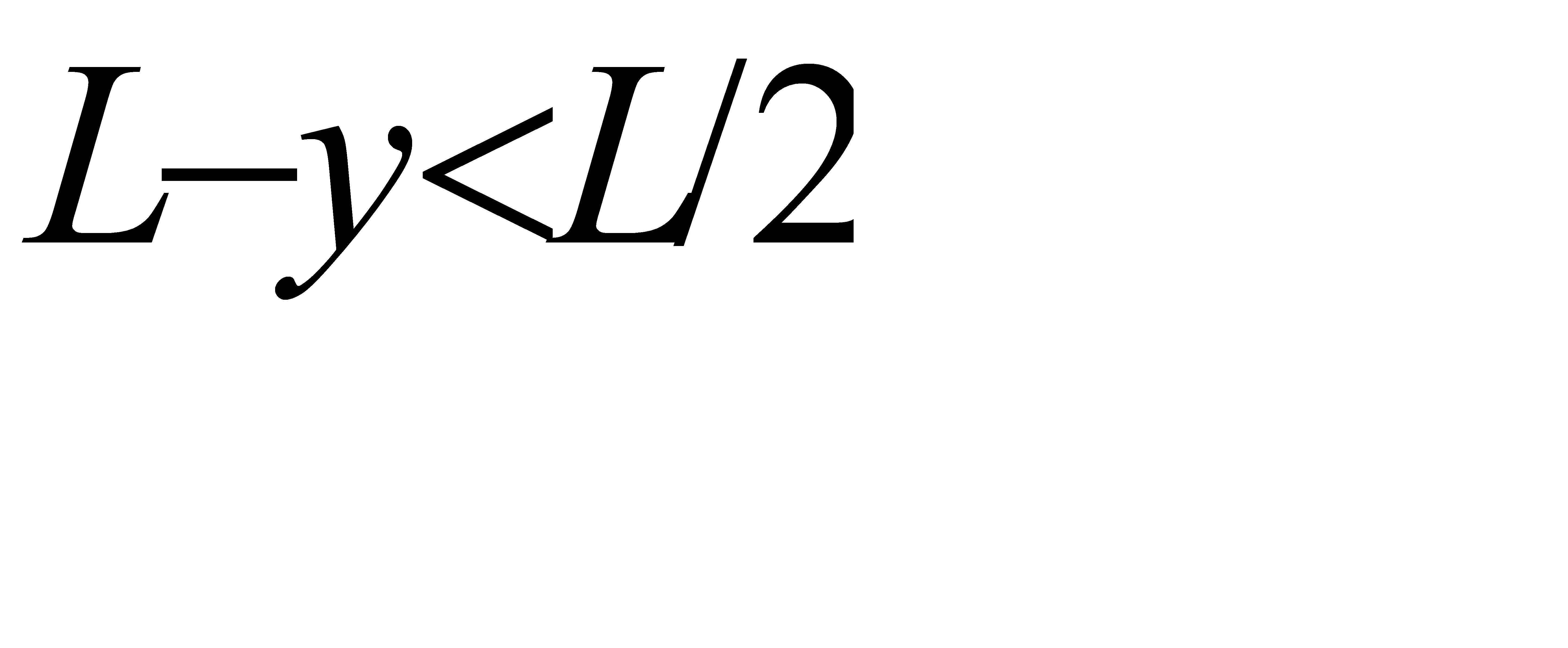 , или, что то же,
, или, что то же,
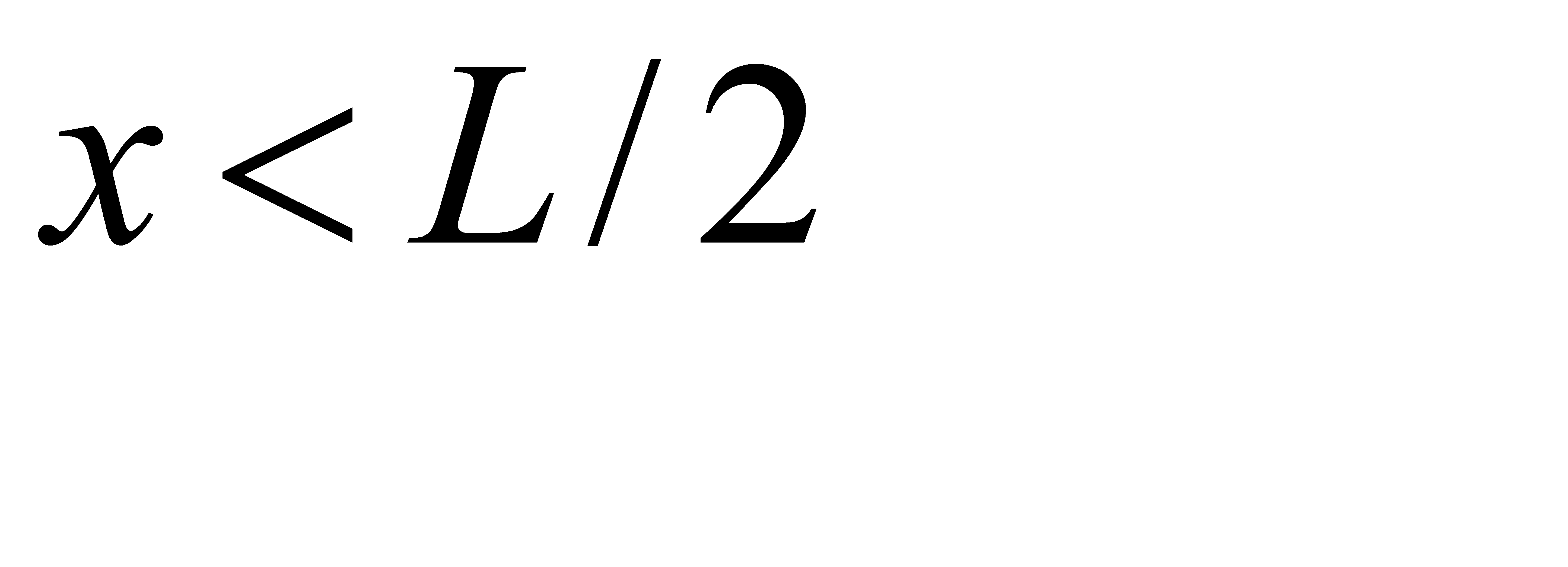 ,
, 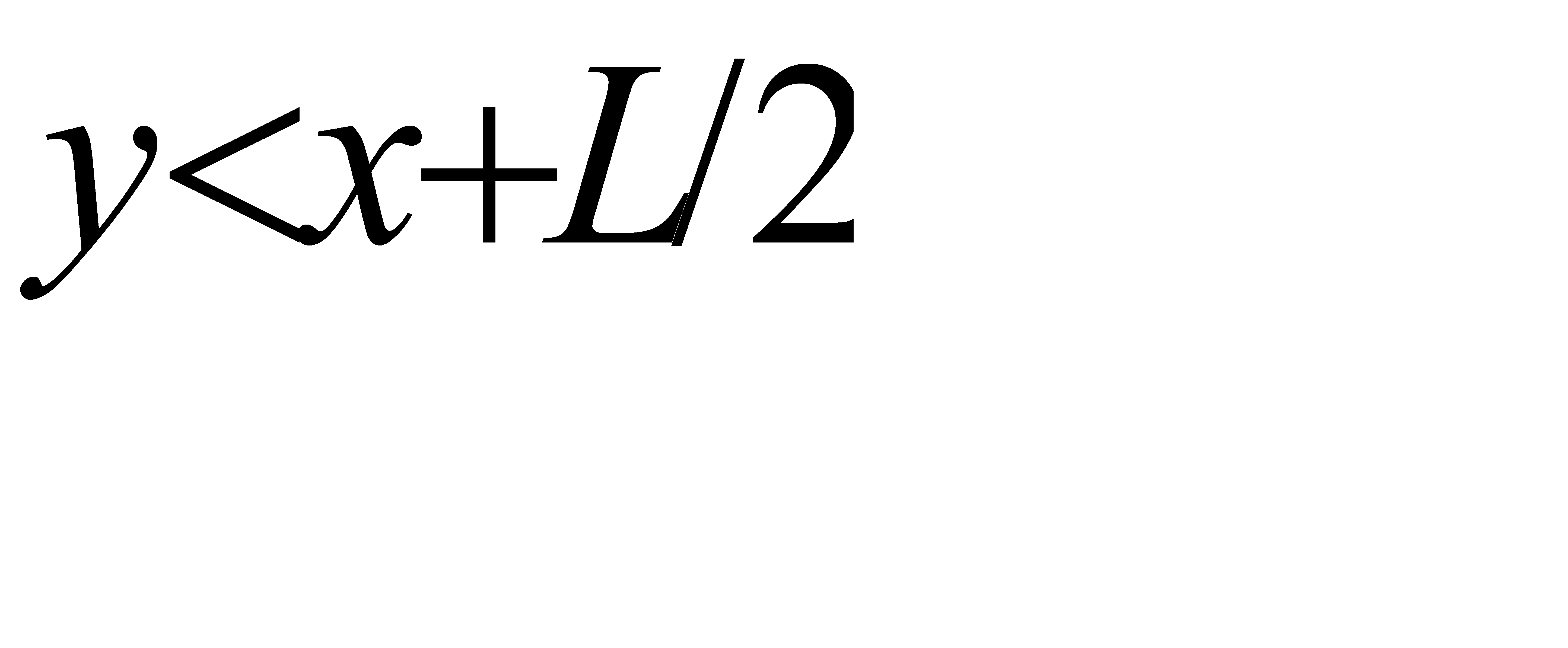 ,
, 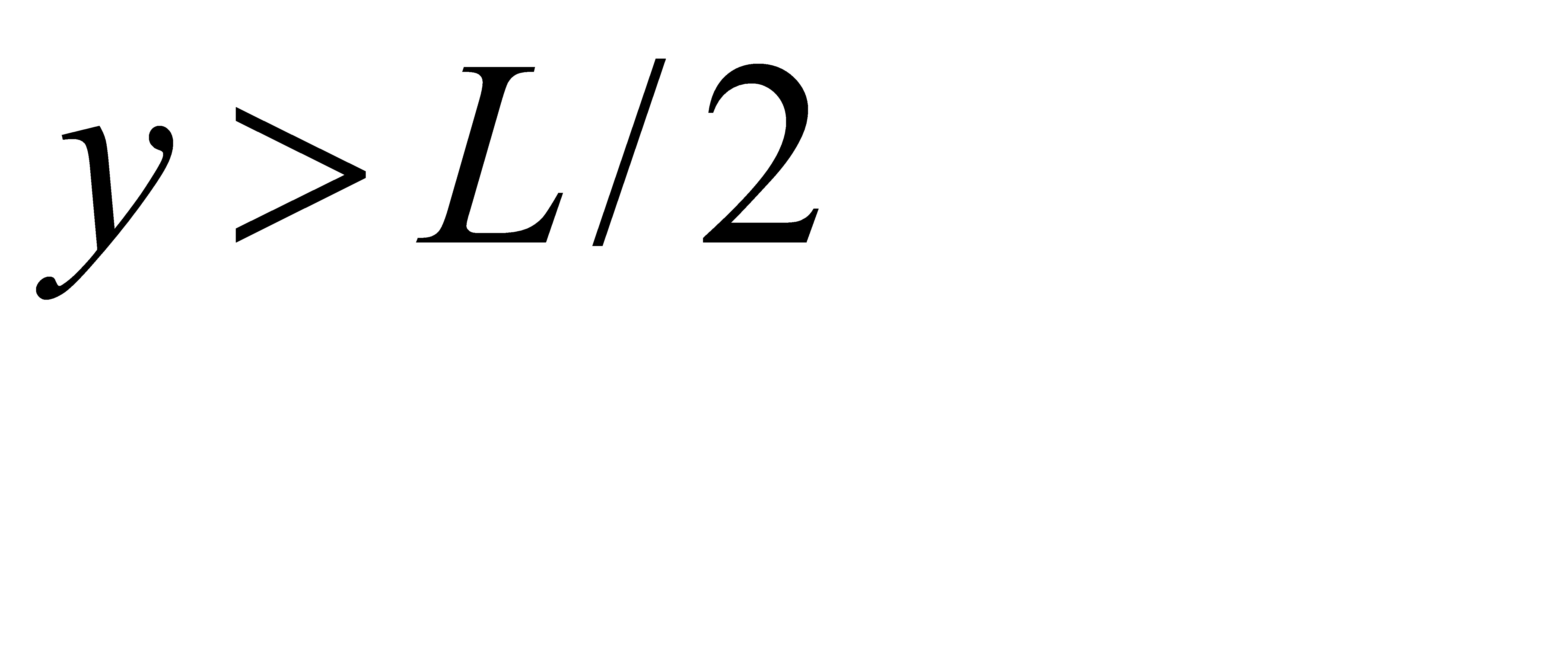 . (*)
. (*)
2. Пусть точка С расположена левее точки В (рис. 3, в). В этом случае должны иметь место неравенства 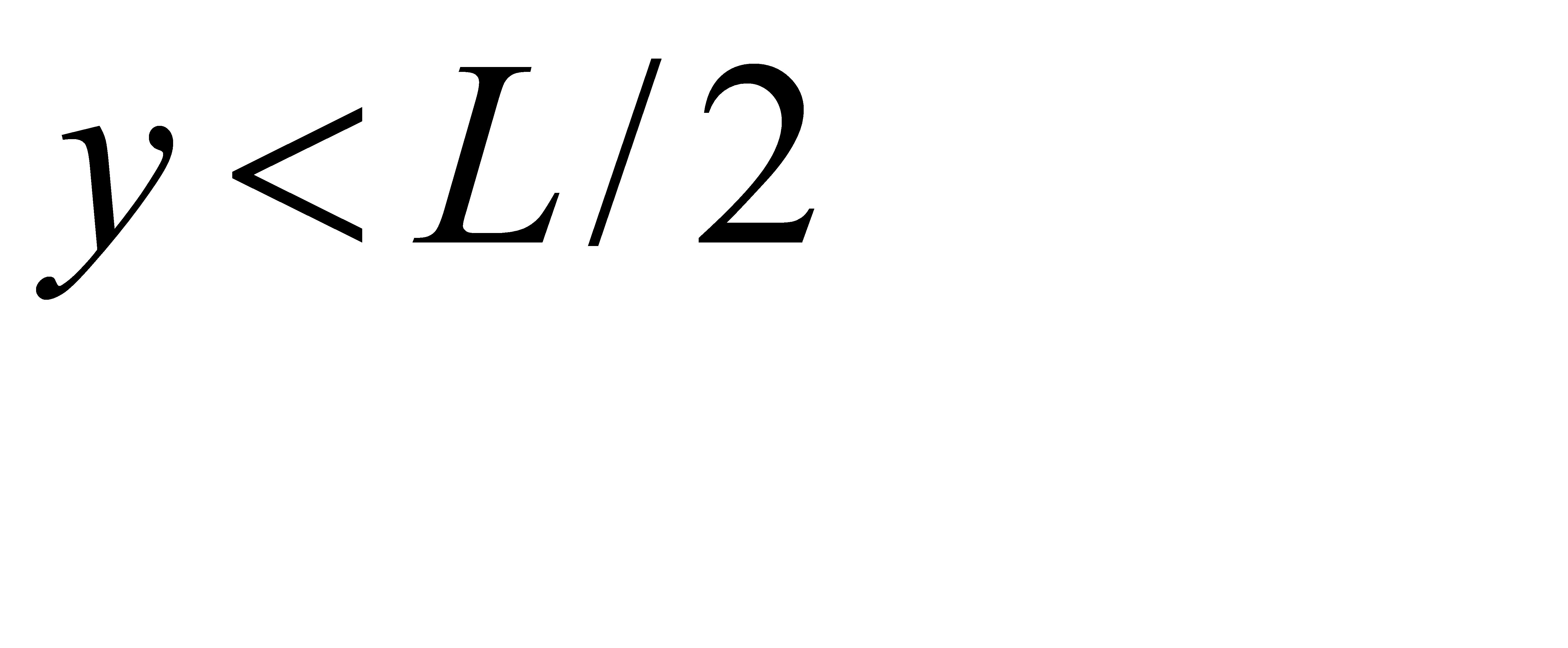 ,
, 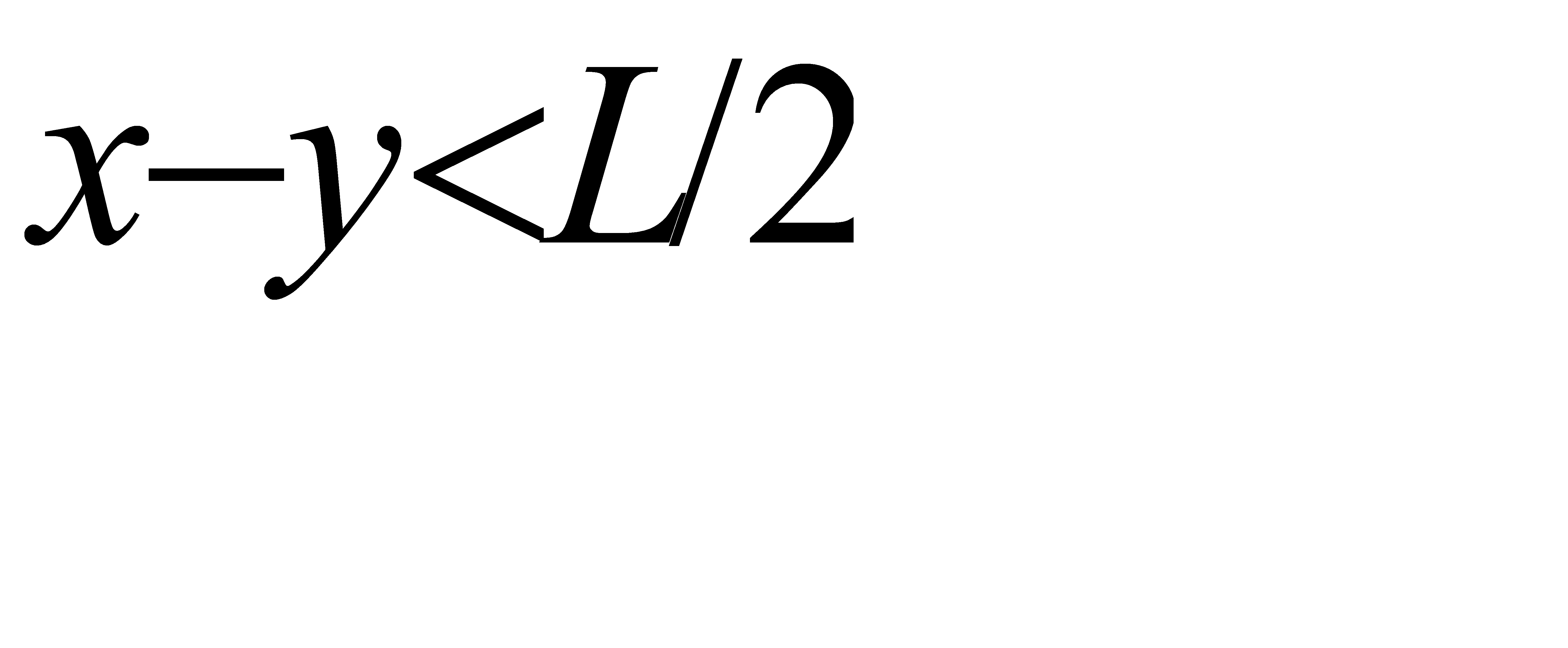 ,
, 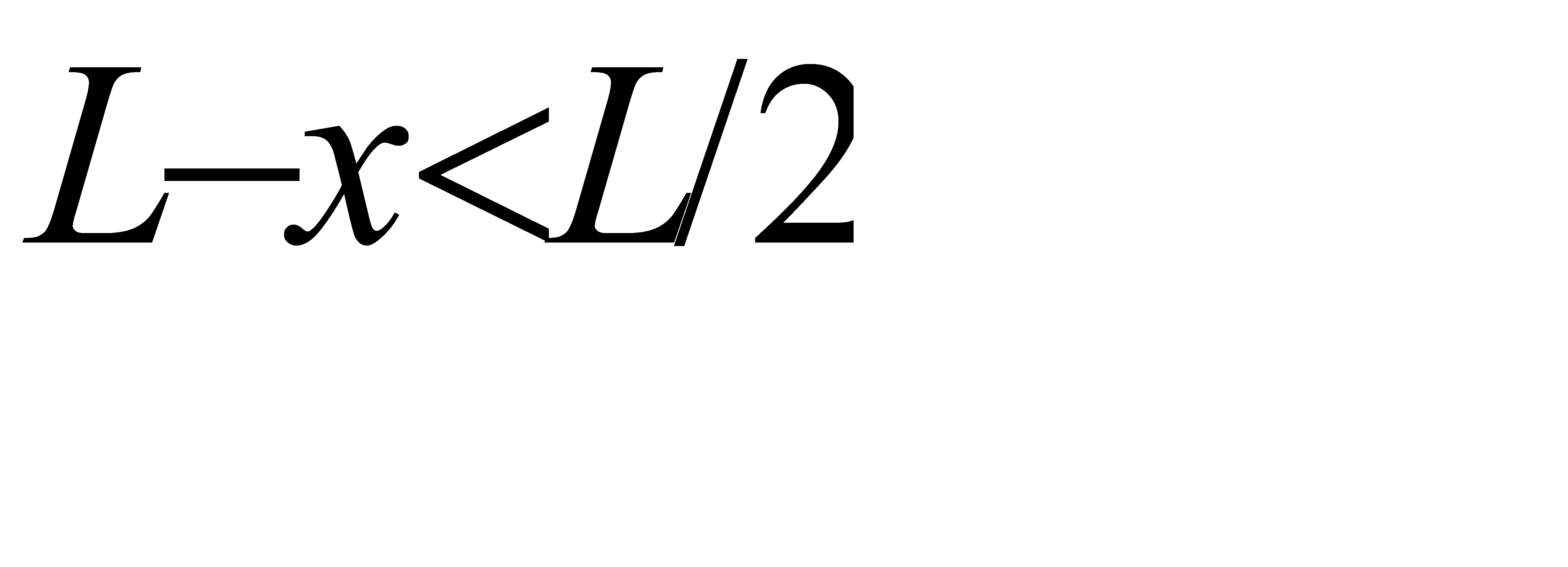 , или, что то же,
, или, что то же,
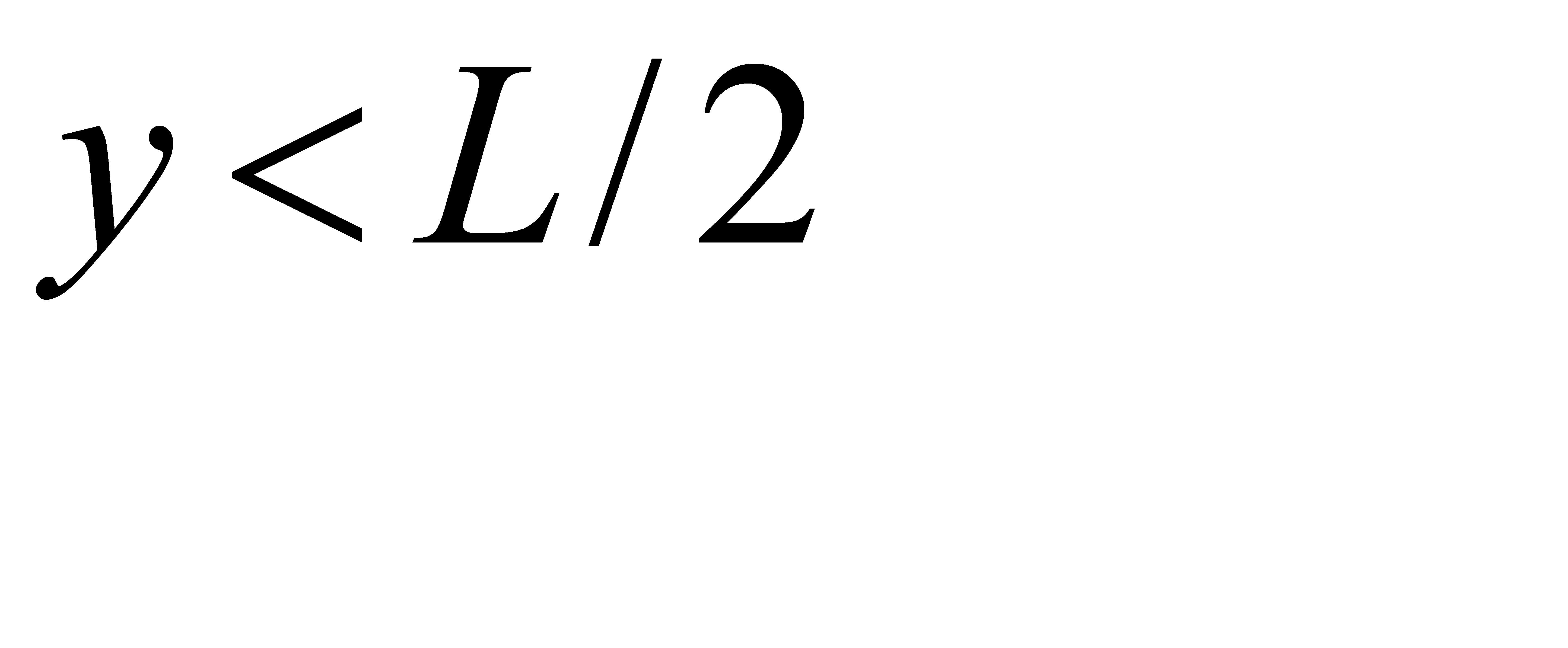 ,
, 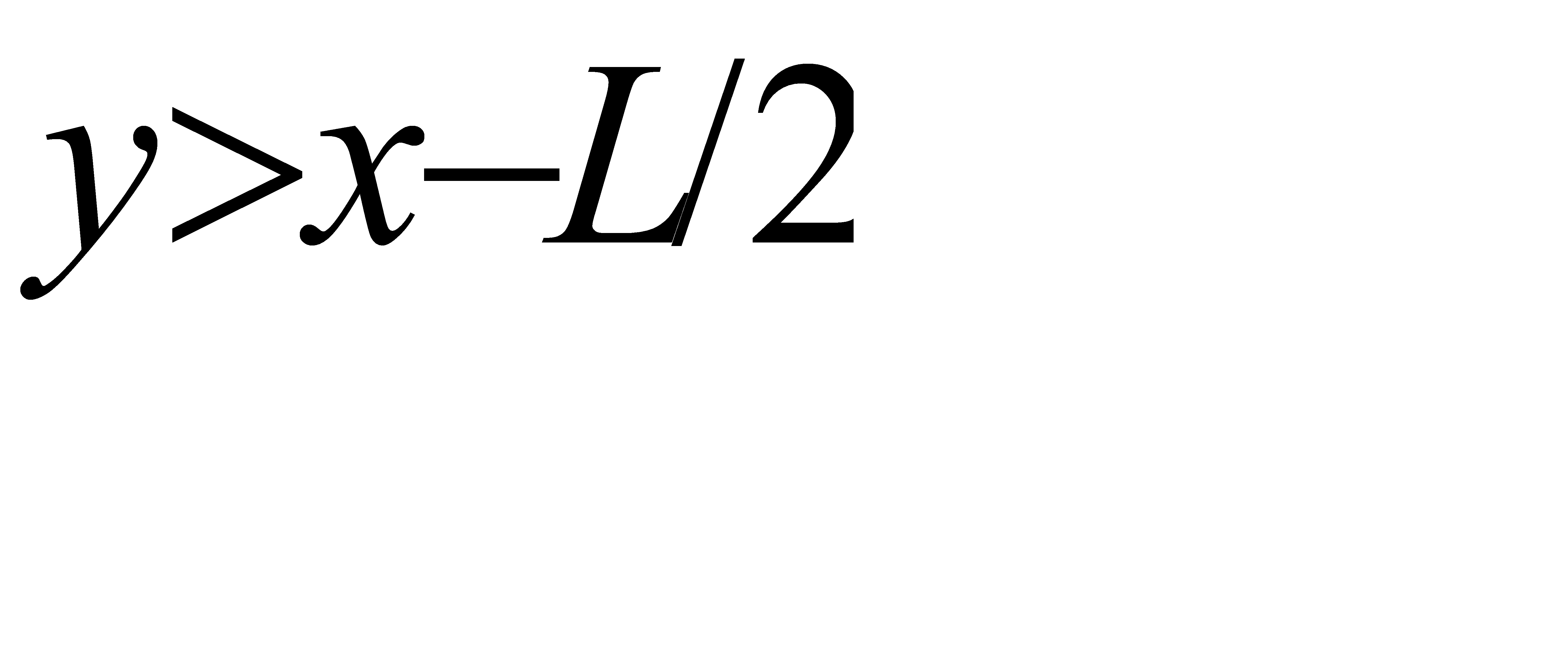 ,
, 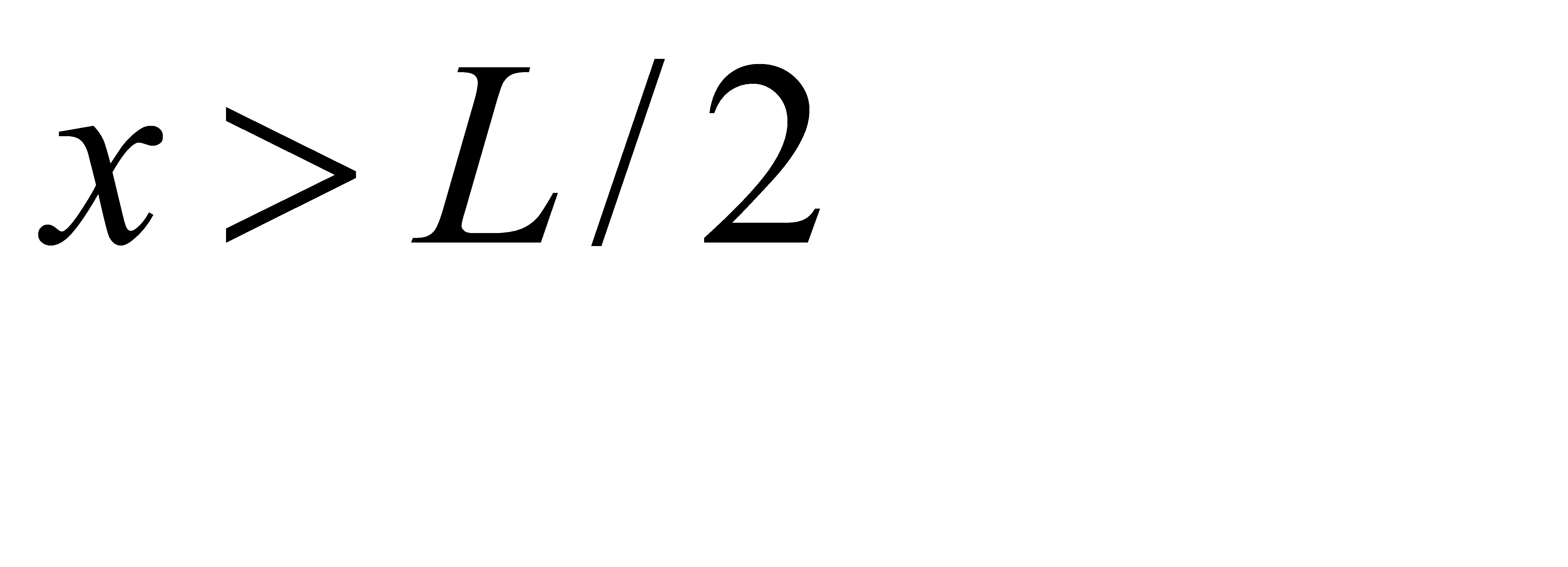 . (**)
. (**)
Как видно из рис. 3. а, неравенства (*) выполняются для координат точек треугольника EFH, а неравенства (**) – для точек треугольника KHM. Таким образом, заштрихованные треугольники можно рассматривать как фигуру g, координаты точек которой благоприятствуют интересующему нас событию (из трёх отрезков можно построить треугольник).
Искомая вероятность
 .
.
#  41 Решение: Обозначим моменты поступления сигналов первого
41 Решение: Обозначим моменты поступления сигналов первого
и второго устройств соответственно через х и у. В силу условия задачи должны выполняться двойные неравенства: 0< х< T, 0< y< T.
Введем в рассмотрение прямоугольную систему координат хОу. В этой системе двойным неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату ОТ AT. Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют все возможные значения моментов поступления сигналов.
Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше t, т. е. если у—х < t при у > х и x — y< tx> y, или, что то же,
у < x+t при у > х, (*)
у> х—t при у < х, (**)
Неравенство (*) выполняется для координат тех точек фигуры G, которые лежат выше прямой у= х и ниже прямой y = x+t; неравенство (**) имеет место для точек, расположенных ниже прямой y=x и выше прямой у = х—t.
Как видно из рис все точки, координаты которых удовлетворяют неравенствам (*) и (**) принадлежат заштрихованному шестиугольнику. Таким образом, этот шестиугольник можно рассматривать как фигуру g. координаты точек которой являются благоприятствующими срабатыванию сигнализатора моментами времени хну.
Искомая вероятность
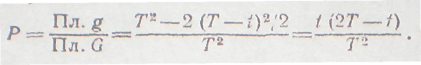
#42
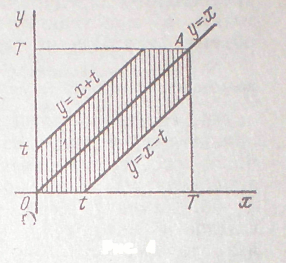
Решение:
Обозначим моменты встречи 2х студентов соответственно через х и у. Они могут встретиться в течение часа(так как 13-12=1). Пусть Т=1. В силу условия задачи должны выполняться двойные неравенства: 0< х< 1, 0< y< 1.
Введем в рассмотрение прямоугольную систему координат хОу. В этой системе двойным неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату ОТ AT. Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют все возможные значения моментов встречи студентов. Так как пришедший первым ждет второго в течение 1/4 часа, после чего уходит, то t=1/4.
Они встретятся, если разность между моментами меньше t, т. е. если у—х < t при у > х и x — y< t, x> y, или, что то же,
у < x+t при у > х, (*)
у> х—t при у < х, (**)
Неравенство (*) выполняется для координат тех точек фигуры G, которые лежат выше прямой у= х и ниже прямой y = x+t; неравенство (**) имеет место для точек, расположенных ниже прямой y=x и выше прямой у = х—t.
Как видно из рис все точки, координаты которых удовлетворяют неравенствам (*) и (**) принадлежат заштрихованному шестиугольнику. Таким образом, этот шестиугольник можно рассматривать как фигуру g. координаты точек которой являются благоприятствующими моментами времени х и у, когда студенты помуг встретиться.
Y
Y=x
T A
t=1/4
1. X
t=1/4 T=1
Искомая вероятность
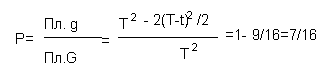 Ответ: 7/16
Ответ: 7/16
#43
РЕШЕНИЕ.
Рассмотрим пространственную систему координат.
A = {из трех наудачу взятых отрезков длиной не более L можно построить треугольник}
Обозначим через x, y и z длины трех выбранных отрезков.
Пространство элементарных исходов имеет вид:
K = {(x, y, z): 0< =x< =L; 0< =y< =L; 0< =z< =L} - куб со стороной длины L 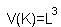
Пространство благоприятных исходов имеет вид:
T = {(x, y, z): 0< =x< =L; 0< =y< =L; 0< =z< =L; x+y> z; x+z> y;
y+z> x} - куб со стороной длины L без трех тетраэдров
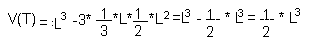
Ответ: 1/2

#44
Решение: Числа удовлетворяют неравенствам . Введём в рассмотрение прямоугольную систему координат xOy. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату OLRM. Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют соответственно все возможные значения координат точек х и у. Согласно условию задачи, имеют место следующие неравенства:
(см. рисунок). Заштрихованную область можно принять за фигуру g, координаты точек которой благоприятствуют интересующему нас событию.
Нетрудно видеть, что
Искомая вероятность
#45 Р ешение. Числа х и у должны удовлетворять неравенствам: . Введём в рассмотрение прямоугольную систему координат xOy. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату OLRM. Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют соответственно все возможные значения координат точек х и у. Согласно условию задачи, имеют место следующие неравенства:
(си. Рисунок). Заштрихованную область можно принять за фигуру g, координаты точек которой благоприятствуют интересующему нас событию.
Нетрудно видеть, что
Искомая вероятность
#46 Решение: Обозначим искомое событие А, а противоположное ему В(ни один из взятых учебников не окажется в переплете). Так как сумма вероятностей двух противоположных событий равно 1, тоР(А)=1-Р(В)
Р(А)=1- С103 /С153=1-24/91=67/91
#47 Решение. Требование – хотя бы одна из взятых деталей окрашена – будет осуществлено, если произойдет любое из следующих трех несовместных событий: B – одна деталь окрашена, C – две детали окрашены, D – три детали окрашены.
Интересующее нас событие A можно представить в виде суммы событий: A=B+C+D. По теореме сложения,
P(A)=P(B)+P(C)+P(D). Найдем вероятность событий B, C и D: 

Получим: 
#48 Доказательство
Событие В можно представить в виде суммы несовместных событий  и
и 
 :
:
 =
=  +
+ 
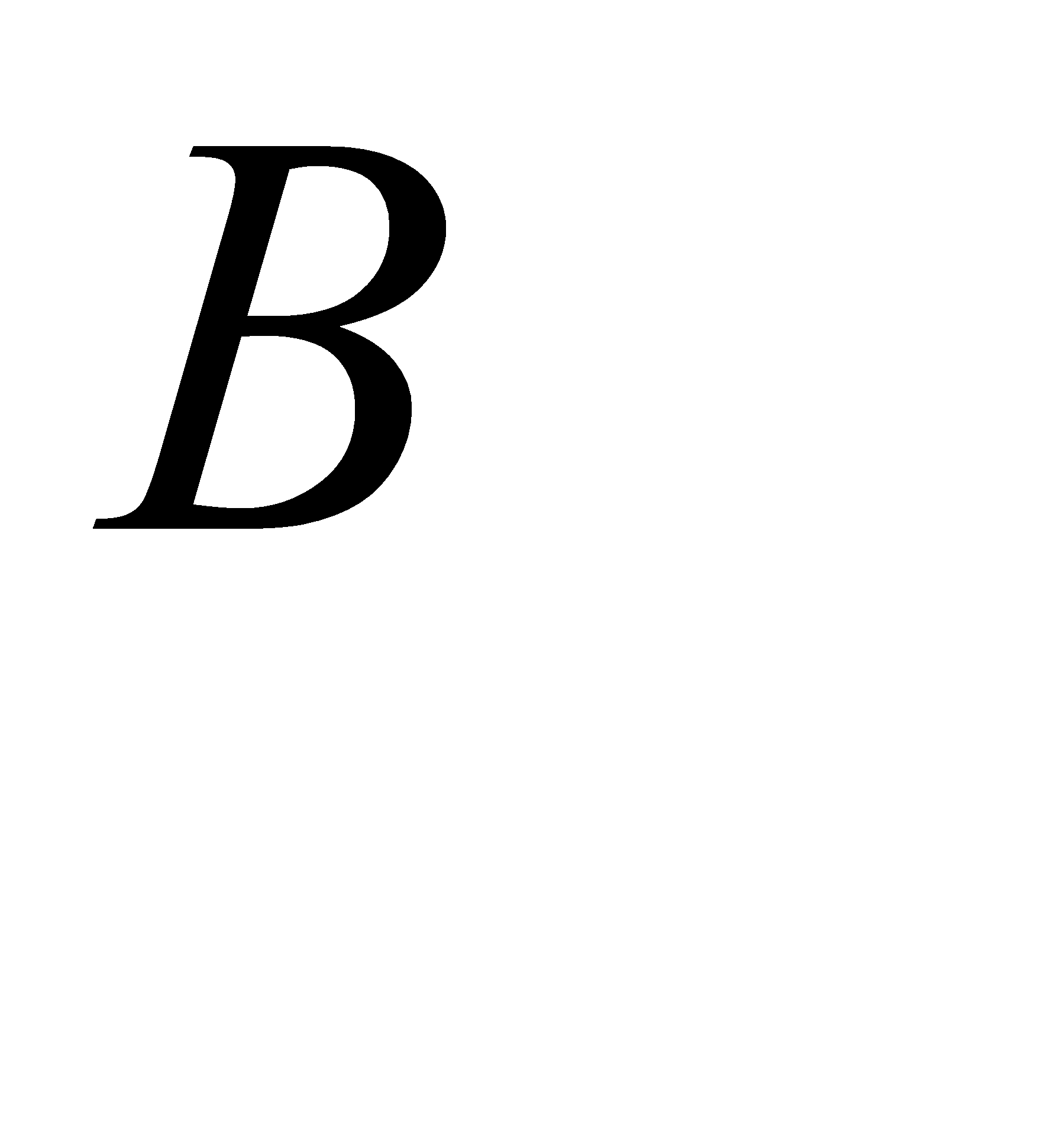 .
.
По теореме сложения вероятностей несовместных событий получим
 .
.
Так как 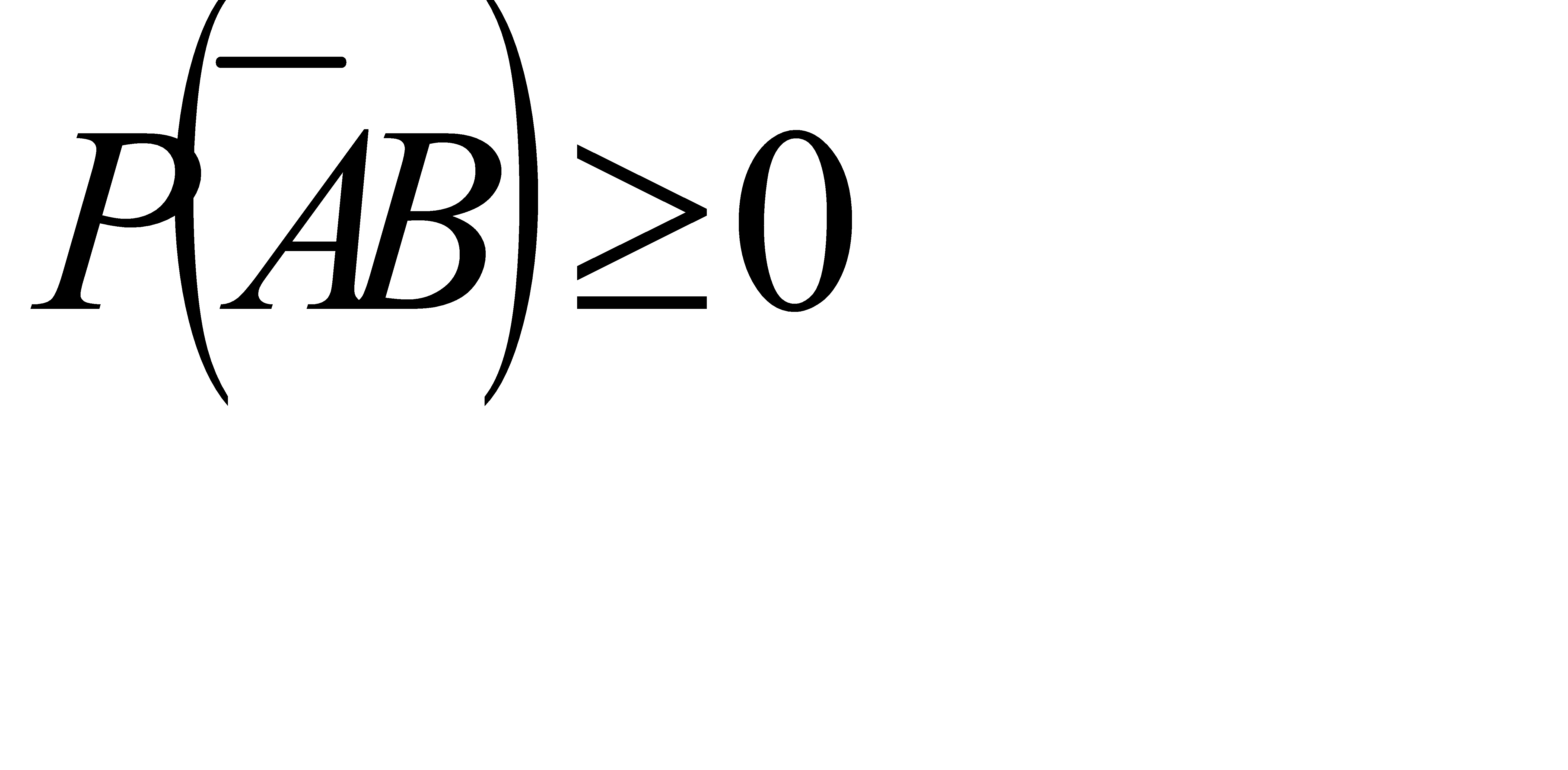 , то
, то 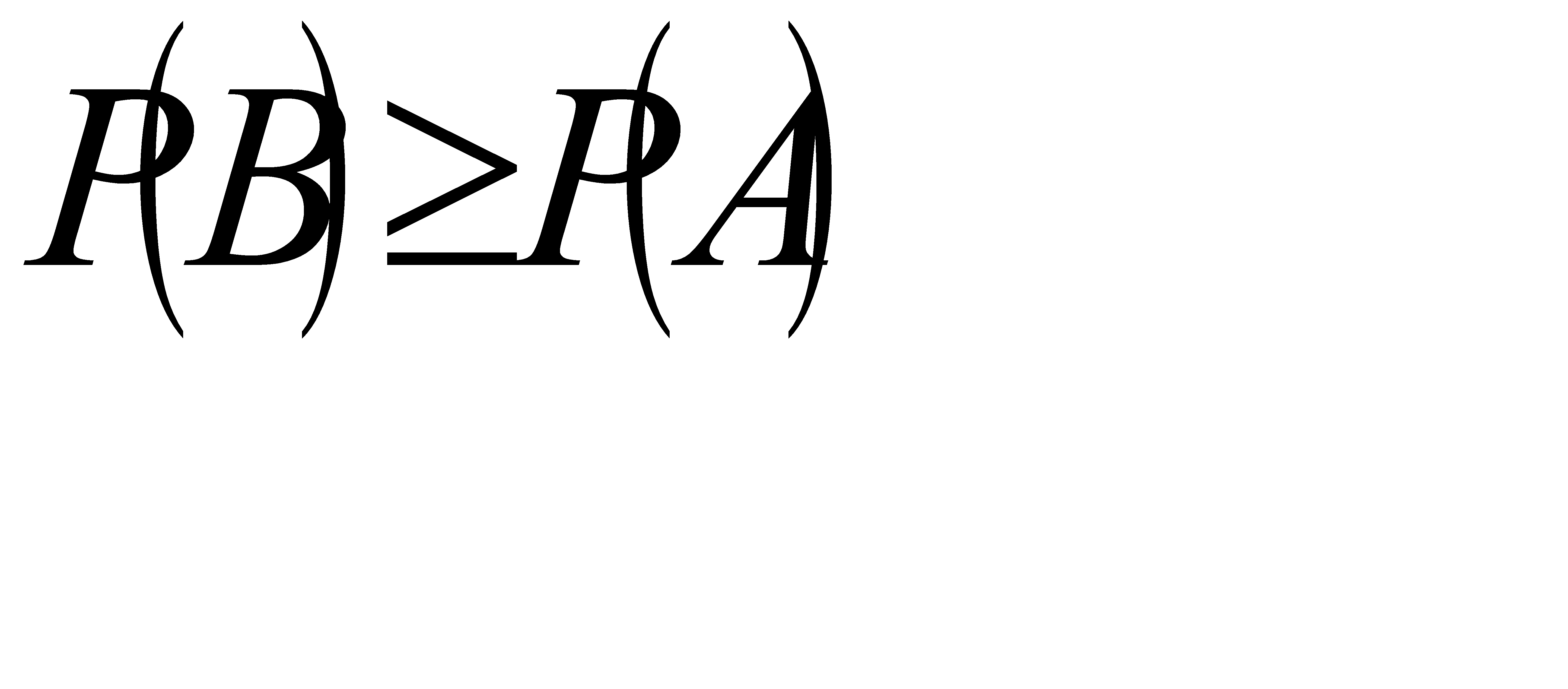 Ч. т. д.
Ч. т. д.
#49 Решение. Введем обозначения событий: В1 – появилось только одно событие А1, В2 – появилось только событие А2.
Появление события В1 равносильно появлению события 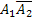 (появилось первое событие и не появилось второе), т. е. В1 =
(появилось первое событие и не появилось второе), т. е. В1 = 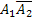 . Появление события В2 равносильно появлению события
. Появление события В2 равносильно появлению события 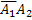 (появилось второе событие и не появилось первое), т. е. В2 =
(появилось второе событие и не появилось первое), т. е. В2 = 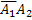 .
.
Таким образом, чтобы найти вероятность появления только одного из событий А1 и А2, достаточно найти вероятность появления одного, безразлично какого, из событий В1 и В2. События В1 и В2 несовместны, поэтому применима теорема сложения: 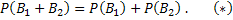
Остается найти вероятности каждого из событий В1 и В2. События А1 и А2 независимы, следовательно, независимы события А1 и 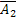 , а также
, а также 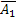 и А2, поэтому применима теорема умножения:
и А2, поэтому применима теорема умножения:
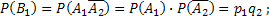
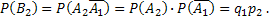
Подставив эти вероятности в соотношение (*), найдем искомую вероятность появления только оного из событий А1 и А2:
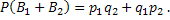
#50 Решение: Введем обозначения событий: 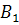 — появилось только событие
— появилось только событие 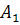 ( Срабатывание первого сигнализатора);
( Срабатывание первого сигнализатора); 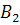 — появилось только событие
— появилось только событие 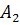 ( Срабатывание второго сигнализатора).
( Срабатывание второго сигнализатора).
Появление события 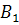 равносильно появлению события
равносильно появлению события 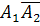 (появилось первое событие и не появилось второе), т. е.
(появилось первое событие и не появилось второе), т. е. 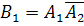 . Появление события
. Появление события 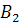 равносильно появлению события
равносильно появлению события 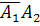 (появилось второе событие и не появилось первое), т. е.
(появилось второе событие и не появилось первое), т. е. 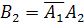 . Таким образом, чтобы найти вероятность появления только одного из событий
. Таким образом, чтобы найти вероятность появления только одного из событий 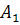 и
и 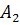 , достаточно найти вероятность появления одного, безразлично какого, из событий
, достаточно найти вероятность появления одного, безразлично какого, из событий 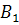 и
и 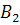 . События
. События 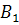 и
и 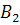 несовместны, поэтому применима теорема сложения:
несовместны, поэтому применима теорема сложения: 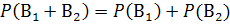
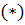 остается найти вероятности каждого из событий
остается найти вероятности каждого из событий 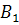 и
и 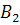 . События
. События 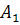 и
и 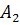 независимы, следовательно, независимы события
независимы, следовательно, независимы события 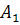 и
и 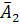 , а также
, а также 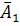 и
и 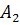 , поэтому применима теорема умножения:
, поэтому применима теорема умножения:


Подставив эти вероятности в соотношение 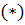 , найдем искомую вероятность появления только одного из событий
, найдем искомую вероятность появления только одного из событий 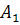 и
и 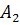 .
. 
#51 Вероятность попадания при одном выстреле для первого стрелка равна 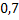 , значит вероятность промаха –
, значит вероятность промаха – 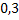 . Для второго –
. Для второго – 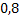 , а промаха –
, а промаха – 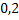 . Потому вероятность того, что при одном залпе в мишень попадет только один из стрелков
. Потому вероятность того, что при одном залпе в мишень попадет только один из стрелков 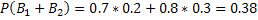 .
.
#52
Решение: Из данных задачи следует, что PA2=0, 8; PB1+B2=0, 38; где A1 и A2 – события попадания в цель первого и второго орудия соответственно. B1и B2 - попадание только одного из соответствующих орудий, т. е. B1 = A1*A2 и B2 = A2*A1. Обозначим как PA1=p. Так как PB1+B2=PB1+ PB2, то подставляя, получим: 0, 38=0, 8-0, 8p+0, 2p. p=0, 7;
Вероятность поражения цели при одном выстреле первым из орудий составляет – 0, 7.
#53 Обозначим за 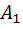 событие, что изделие 1 - стандартно
событие, что изделие 1 - стандартно
Обозначим за 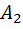 событие, что изделие 2 - стандартно
событие, что изделие 2 - стандартно
Событие Ā 1 означает, что изделие 1 - нестандартно
Событие Ā 2 означает, что изделие 2 - нестандартно
Тогда по теореме умножения вероятностей получаем, что вероятность того, что первое изделие стандартно, а второе – нет, равна 0, 09
( 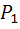 = P(
= P( 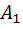 *Ā 2)=P(
*Ā 2)=P( 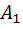 )*P(Ā 2)=0. 9*0. 1=0. 09)Соответственно вероятность обратного события (изделие 2 – стандартно, а изделие 1 - нестандартно) такая же(
)*P(Ā 2)=0. 9*0. 1=0. 09)Соответственно вероятность обратного события (изделие 2 – стандартно, а изделие 1 - нестандартно) такая же( 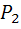 = P
= P 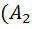 *Ā 1)=P(
*Ā 1)=P( 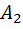 )*P(Ā 1)=0. 9*0. 1=0. 09)Тогда по теореме сложения вероятностей несовместных событий получаем, что вероятность того, что одно изделие стандартно, а другое – нет, равна 0, 18(P((
)*P(Ā 1)=0. 9*0. 1=0. 09)Тогда по теореме сложения вероятностей несовместных событий получаем, что вероятность того, что одно изделие стандартно, а другое – нет, равна 0, 18(P(( 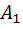 *Ā 2)+
*Ā 2)+ 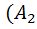 *Ā 1))= P(
*Ā 1))= P( 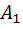 *Ā 2)+ P
*Ā 2)+ P 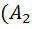 *Ā 1)=
*Ā 1)= 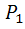 +
+ 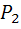 = 0. 09+0. 09=0. 18)
= 0. 09+0. 09=0. 18)
Ответ: 0, 18
#54 Решение: Обозначим допущение ошибки, превышающей заданную точность, в измерениях 1, 2 и 3 как А1, А2 и А3 соответственно. Так как эти события независимы, то по теореме умножения вероятностей независимых событий искомая вероятность будет вычисляться по формуле:
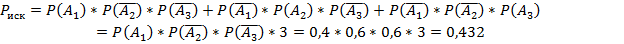
Ответ: 0, 432.
#55 Решение: Обозначим появления товаров высшего сорта 1, 2 и 3 как А1, А2 и А3 соответственно. Так как эти события независимы, то по теореме умножения вероятностей независимых событий искомая вероятность будет вычисляться по формуле:
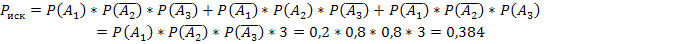
Ответ: 0, 384.
#56 Решение. Введем обозначение событий: безотказно работало первое устройство - A1; безотказно работало второе устройство - А2; безотказно работало третье устройство - A3.
B1 – безотказно работала за время t первое устройство A1; B2 – безотказно работало за время t второе устройство А2; B3 – безотказно работало за время t третье устройство A3.
а) Появление события B1 равносильно появлению события A1 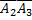 ;
; 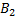 равносильно появлению события A2
равносильно появлению события A2 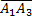 ;
; 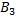 равносильно появлению A3
равносильно появлению A3 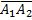 . Таким образом, чтобы найти вероятность появления только одного из событий
. Таким образом, чтобы найти вероятность появления только одного из событий  ,
, 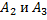 достаточно найти вероятность появления одного, безразлично какого, из событий
достаточно найти вероятность появления одного, безразлично какого, из событий 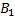 ,
, 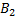 и
и 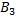 . События
. События 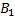 ,
, 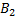 и
и 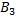 несовместы, поэтому применима теорема сложения: P (
несовместы, поэтому применима теорема сложения: P ( 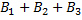 ) = P(
) = P( 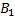 )+ P(
)+ P( 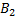 )+ P(
)+ P( 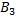 ). (*)
). (*)
Остается найти вероятности каждого из событий 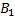 ,
, 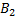 и
и 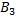 . События
. События  ,
, 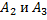 независимы, поэтому применима теорема умножения: P (
независимы, поэтому применима теорема умножения: P ( 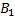 ) =P (A1
) =P (A1 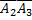 ) =
) = 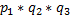 ;
;
P ( 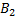 ) =P (A2
) =P (A2 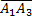 ) =
) = 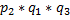 ;
;
P ( 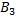 ) =P (A3
) =P (A3 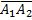 ) =
) = 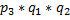 .
.
Подставив эти вероятности в соотношение (*), найдем искомую вероятность появления только одного из событий  ,
, 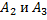 : P (
: P ( 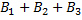 ) =
) = 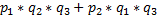 +
+ 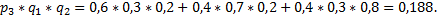
Б) Появление события B1 равносильно появлению события A1 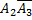 ;
; 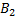 равносильно появлению события A1
равносильно появлению события A1 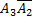 ;
; 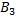 равносильно появлению A3
равносильно появлению A3 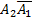 . Аналогично предыдущему решению:
. Аналогично предыдущему решению:
P ( 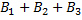 ) =
) = 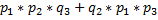 +
+ 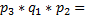 0, 6*0, 7*0, 2+0, 6*0, 3*0, 8+0, 4*0, 7*0, 8=0, 452.
0, 6*0, 7*0, 2+0, 6*0, 3*0, 8+0, 4*0, 7*0, 8=0, 452.
В) Пусть  - безотказная работа всех устройств. Тогда событие B равносильно появлению
- безотказная работа всех устройств. Тогда событие B равносильно появлению 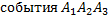 , поэтому P(B)=P(
, поэтому P(B)=P( 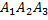 )=
)= 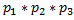 =0, 6*0, 7*0, 8=0, 336.
=0, 6*0, 7*0, 8=0, 336.
#57 Решение.  - детали нет ни в одном из ящиков,
- детали нет ни в одном из ящиков, 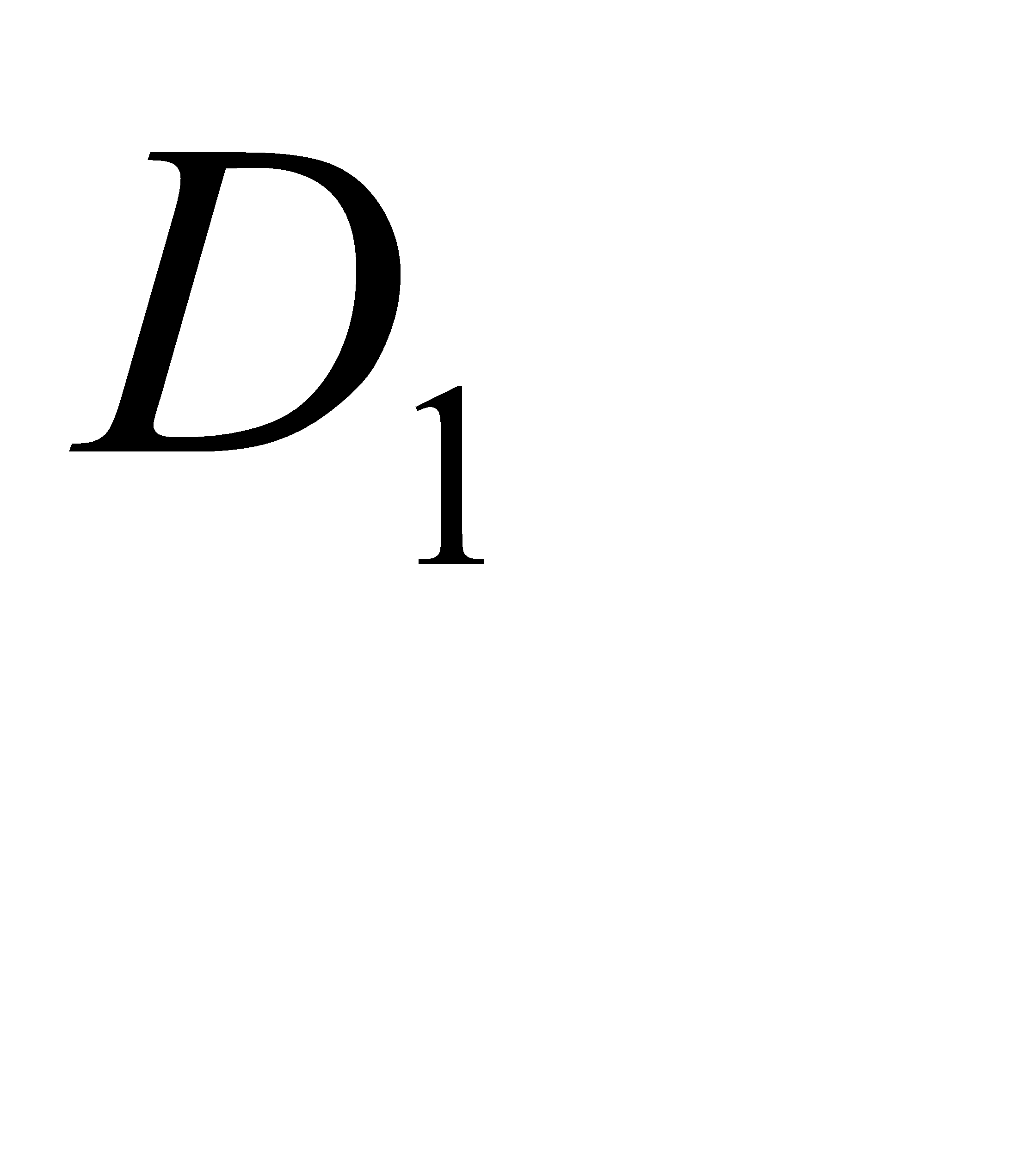 - деталь содержится в одном ящике,
- деталь содержится в одном ящике,  - в двух,
- в двух, 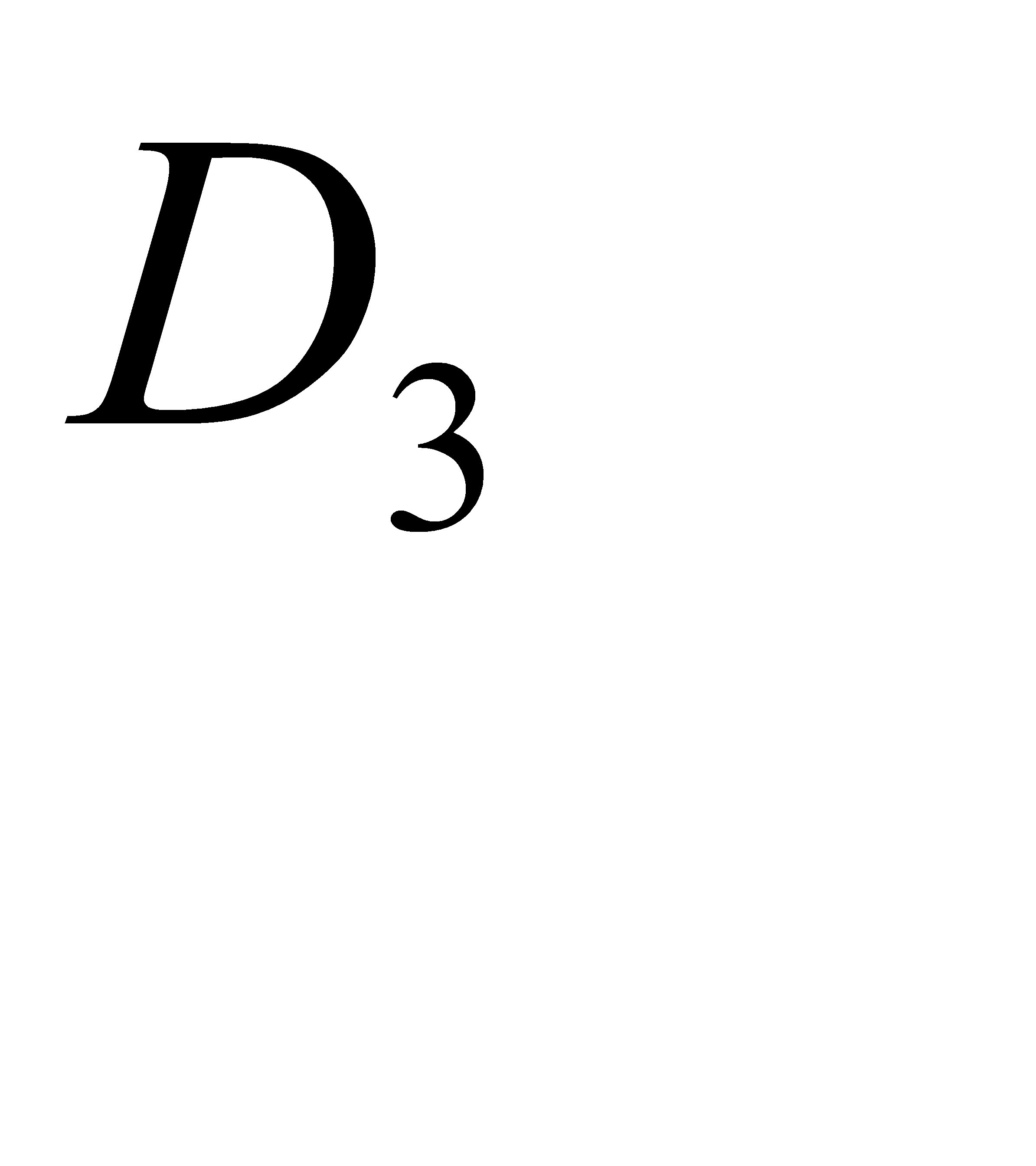 - в трёх,
- в трёх, 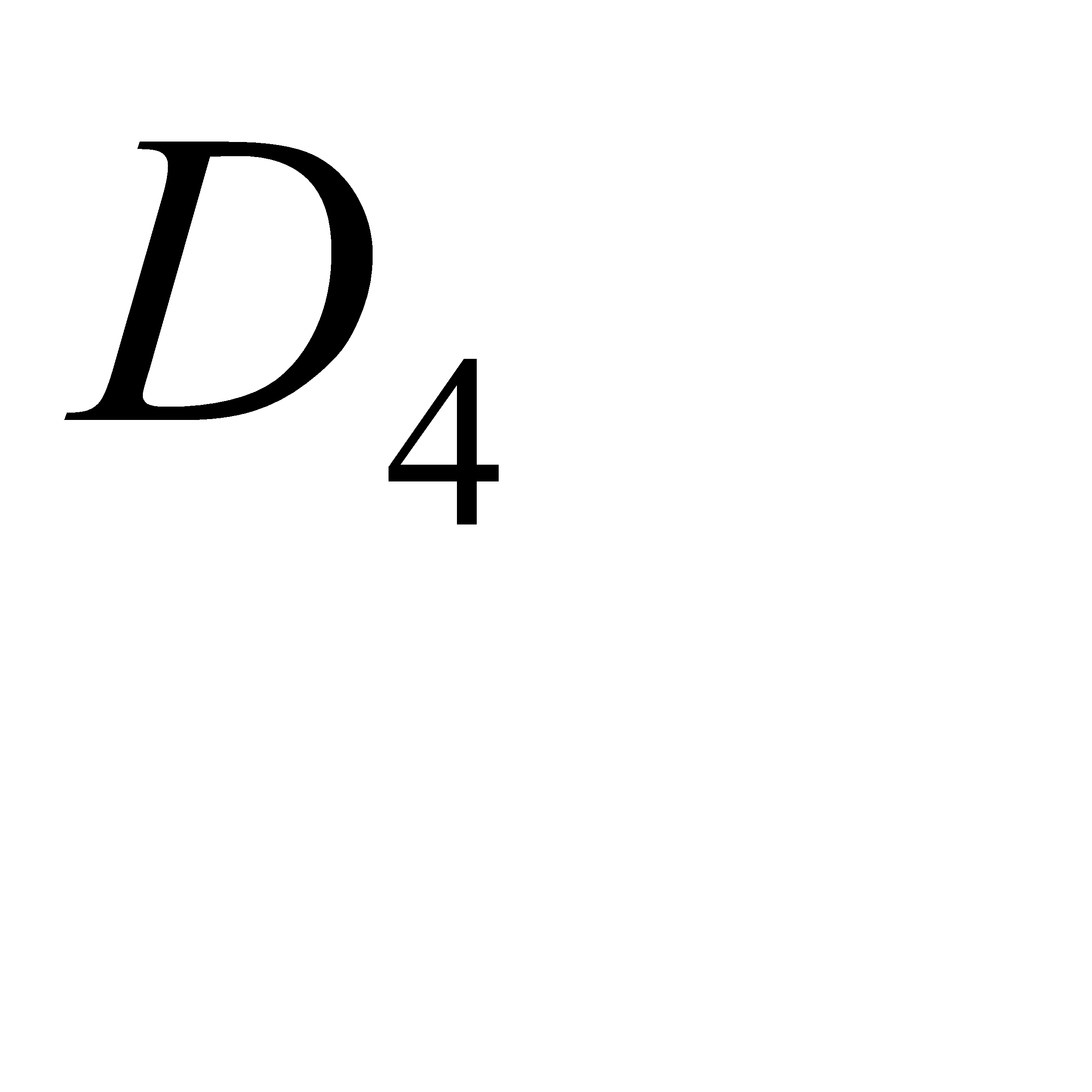 - в четырёх. Эти события несовместны и образуют полную группу, поэтому
- в четырёх. Эти события несовместны и образуют полную группу, поэтому 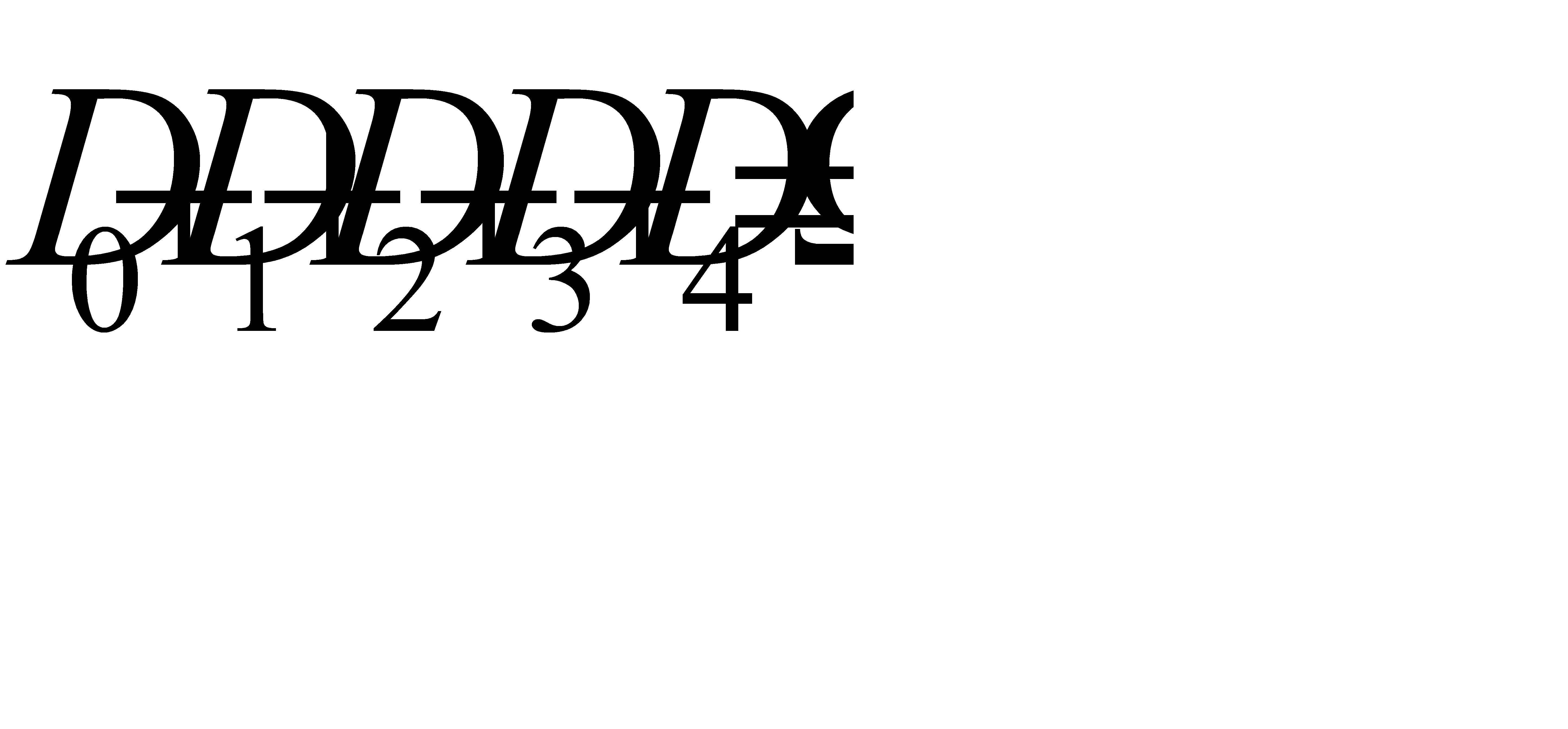 .
.
а)  .
.
Искомая вероятность равна вероятности того, что деталь содержится не во всех четырёх ящиках.  .
.
б)  .
.

 .
.
#58 Решение: а) Вероятность выпадения на одной игральной кости пяти очков равна p=1/6.
Тогда вероятность совместного появления 3 одинаковых событий равна P(A)=p*p*p=1/216.
б) Из первого решения видно, что вероятность появления на каждой из 3 граней одного определенного очка равна P(A)=p*p*p=1/216. Так как таких вариантов 6 ( по числу граней кости), то вероятность появления одинаковых очков равна P(B)=6*P(A)=6*1/216=1/36.
#59 РЕШЕНИЕ. а) Вероятность того, что на выпавших двух гранях появится одно очко, равна 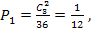 а вероятность того, что на другой грани появится другое количество очков, равна
а вероятность того, что на другой грани появится другое количество очков, равна 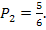
Искомую вероятность найдем по теореме умножения вероятностей: 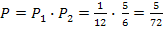 .
.
б) Вероятность того, что на некоторых двух гранях выпадет одинаковое число очков, равна 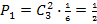 , а вероятность того, что на третьей грани выпадет другое число очков, равна
, а вероятность того, что на третьей грани выпадет другое число очков, равна 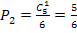 . Искомую вероятность найдем по теореме умножения вероятностей
. Искомую вероятность найдем по теореме умножения вероятностей 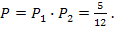
в) Количество благоприятствующих исходов равно 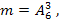 общее количество элементарных исходов равно
общее количество элементарных исходов равно 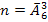 , искомая вероятность равна:
, искомая вероятность равна: 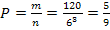 .
.
#60 Решение: Введем обозначения событий: 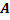 - ни на одной из выпавших граней не появится 6 очков;
- ни на одной из выпавших граней не появится 6 очков; 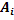 – на выпавшей грани
– на выпавшей грани 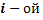 кости
кости  не появится 6 очков.
не появится 6 очков.
Интересующее нас событие 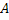 состоит в совмещении событий
состоит в совмещении событий 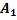 ,
, 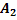 , …,
, …, 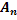 , т. е.
, т. е. 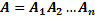
Вероятность того, что на любой выпавшей грани появится число очков, не равное шести, равна 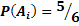
События 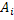 независимы в совокупности, поэтому применима теорема умножения:
независимы в совокупности, поэтому применима теорема умножения:
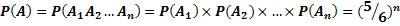
По условию, 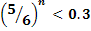 . Следовательно,
. Следовательно, 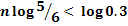 . Отсюда, учитывая, что
. Отсюда, учитывая, что  , найдем:
, найдем: 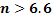 . Таким образом, искомое число игральных костей
. Таким образом, искомое число игральных костей 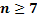
#68 Решение: а) введем обозначение событий: А – выпал шар с номером 1, В – выпал шар с номером 4, С – выпал шар с номером 5. Вероятность наступления события А – Р(А) =  . Вероятность наступления события В при условии, что событие А уже наступило -
. Вероятность наступления события В при условии, что событие А уже наступило - 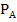 (В) =
(В) =  , вероятность события С при условии А, В -
, вероятность события С при условии А, В - 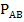 (С) =
(С) =  . Искомая вероятность того, что последовательно выпадут шары с номерами 1, 4, 5 по правилу умножения равна произведению вероятностей событий А, В, С: Р =
. Искомая вероятность того, что последовательно выпадут шары с номерами 1, 4, 5 по правилу умножения равна произведению вероятностей событий А, В, С: Р = 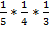 =
=  ≈ 0, 016б) вероятность того, что шары с номерами 1, 4, 5 выпадут в произвольной последовательности равна произведению вероятностей событий А, В, С и количества возможных последовательностей, которые могут составить номера шаров:
≈ 0, 016б) вероятность того, что шары с номерами 1, 4, 5 выпадут в произвольной последовательности равна произведению вероятностей событий А, В, С и количества возможных последовательностей, которые могут составить номера шаров:
Р = 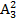
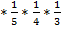 =
= 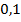
#69 Решение: введём обозначения событий: А – студент знает ответ на первый вопрос, В – студент знает ответ на второй вопрос, С – студент знает ответ на третий вопрос. Вероятность события А равна отношению количества вопросов которые знает студент, к общему количеству вопросов: Р(А) = 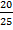 =
=  . Вероятность события В при условии А -
. Вероятность события В при условии А - 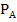 (В) =
(В) = 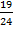 , вероятность С при условии А, В -
, вероятность С при условии А, В - 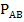 (С) =
(С) = 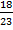 . Вероятность того, что студент знает все три вопроса по правилу умножения вероятностей равна: Р =
. Вероятность того, что студент знает все три вопроса по правилу умножения вероятностей равна: Р = 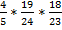 =
=  ≈ 0, 23.
≈ 0, 23.
#70 Решение: a) введем обозначение событий: А – выпал кубик с номером 1, В – выпал кубик с номером 2, С – выпал кубик с номером 3. Вероятность наступления события А – Р(А) =  . Вероятность наступления события В при условии, что событие А уже наступило -
. Вероятность наступления события В при условии, что событие А уже наступило - 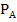 (В) =
(В) =  , вероятность события С при условии А, В -
, вероятность события С при условии А, В - 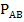 (С) =
(С) =  . Искомая вероятность того, что при вынимании без возврата выпадут кубики с номерами 1, 2, 3 по правилу умножения равна произведению вероятностей событий А, В, С: Р =
. Искомая вероятность того, что при вынимании без возврата выпадут кубики с номерами 1, 2, 3 по правилу умножения равна произведению вероятностей событий А, В, С: Р = 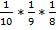 =
= 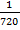 .
.
б) вероятность того, что выпадут кубики с номерами 1, 2, 3 при вынимании их с возвращением обратно равна произведению равных вероятностей событий А, В, С:
Р = 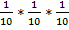 =
= 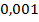 .
.
#71 Решение: По условию, 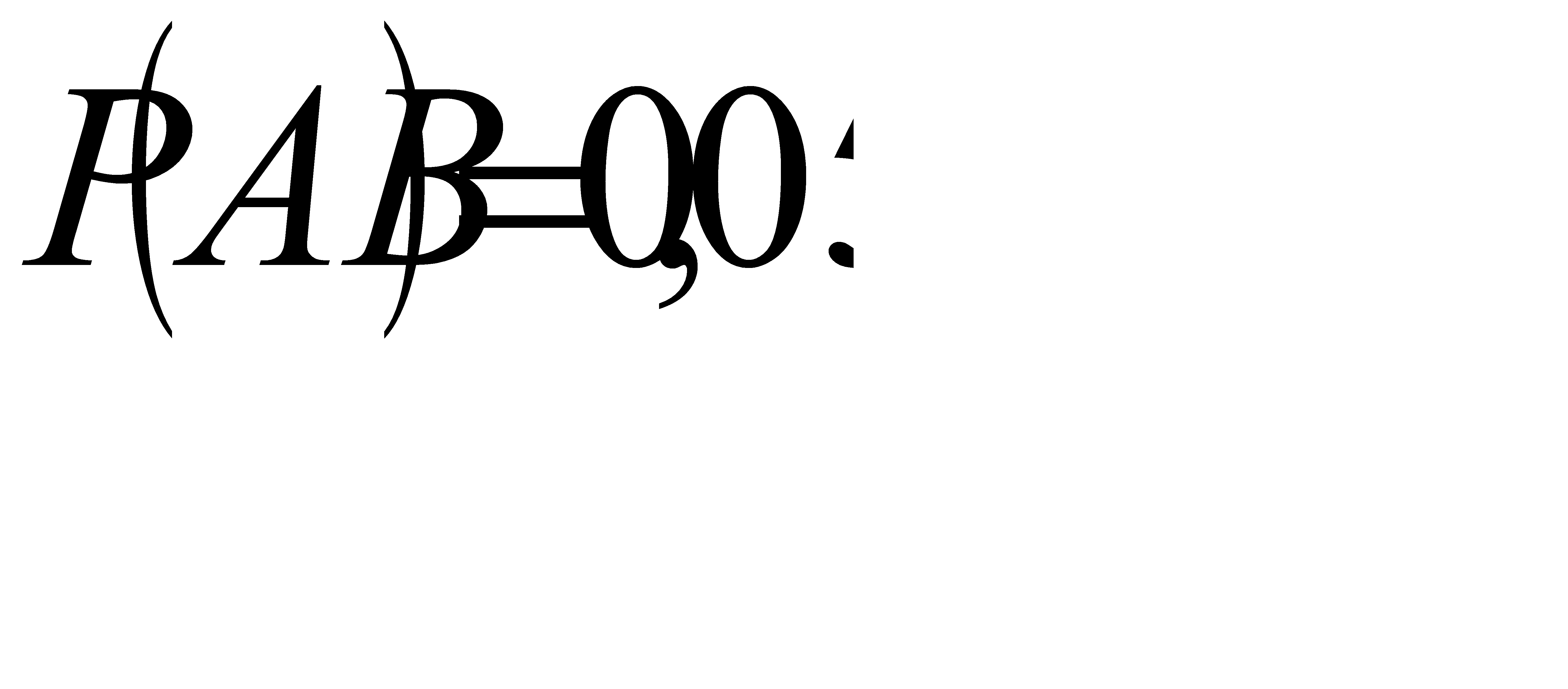
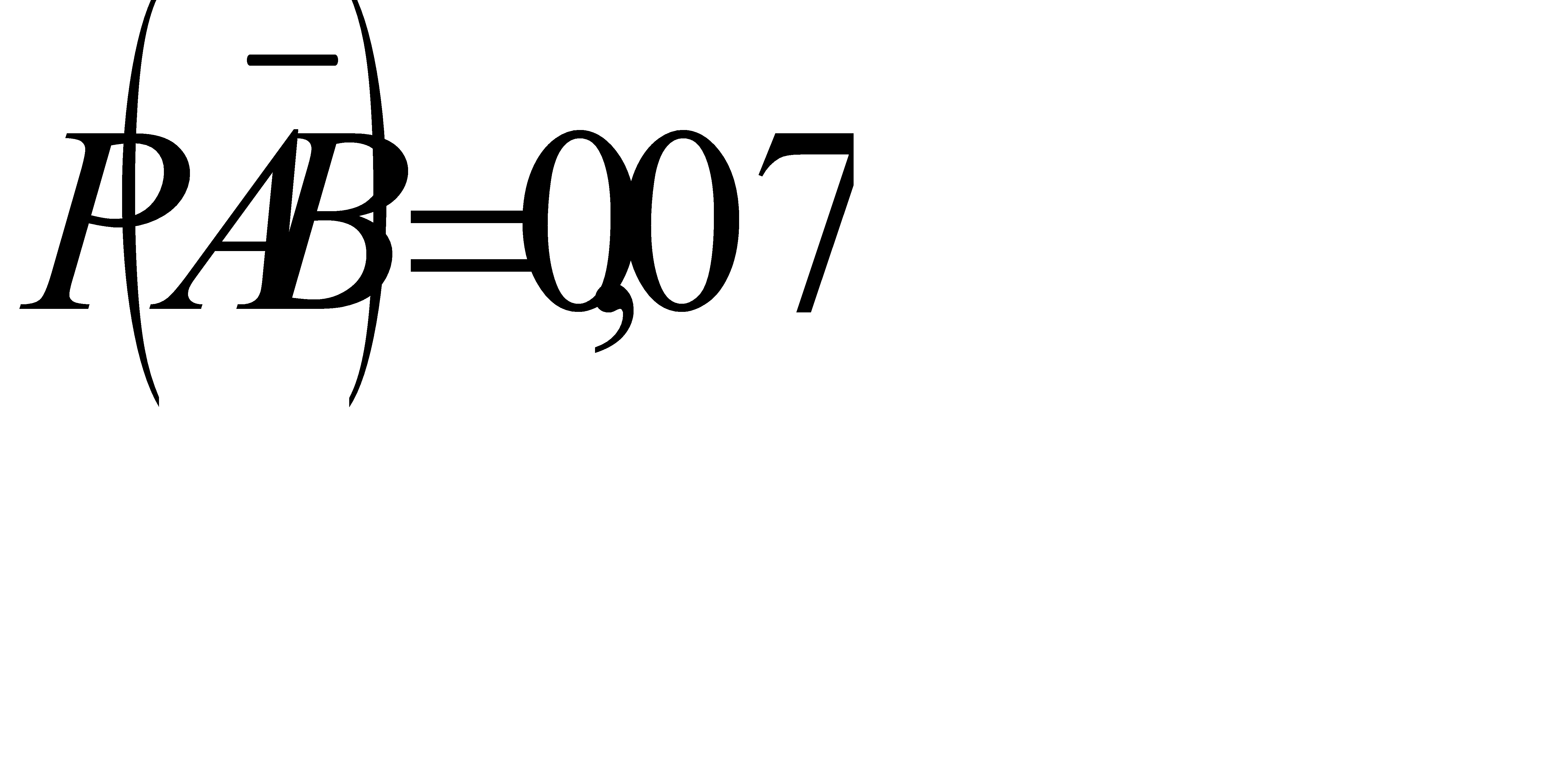

Найдем условную вероятность того, что сын темноглазый если отец темноглазый:

Найдем условную вероятность того, что сын светлоглазый, если отец темноглазый:

Найдем условную вероятность того, что сын темноглазый, если отец светлоглазый:

Найдем условную вероятность того, что сын светлоглазый, если отец светлоглазый:

#72 Найти вероятность Р(А) по данным вероятностям:
Р(АВ)=0, 72, Р(А 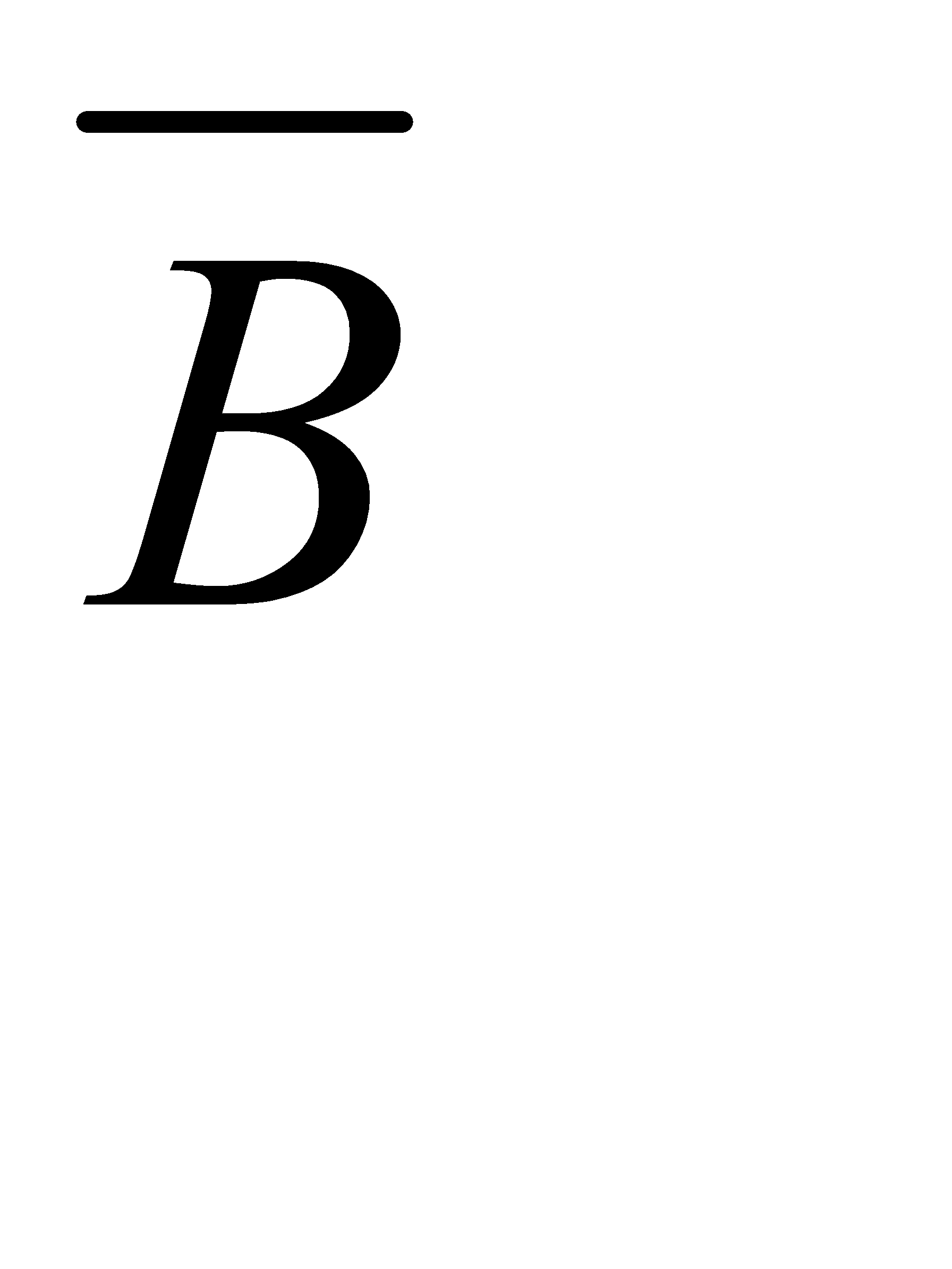 )=0, 18.
)=0, 18.
Решение.
Событие А можно представить в виде суммы следующих двух несовместных событий:
А=АВ+ А 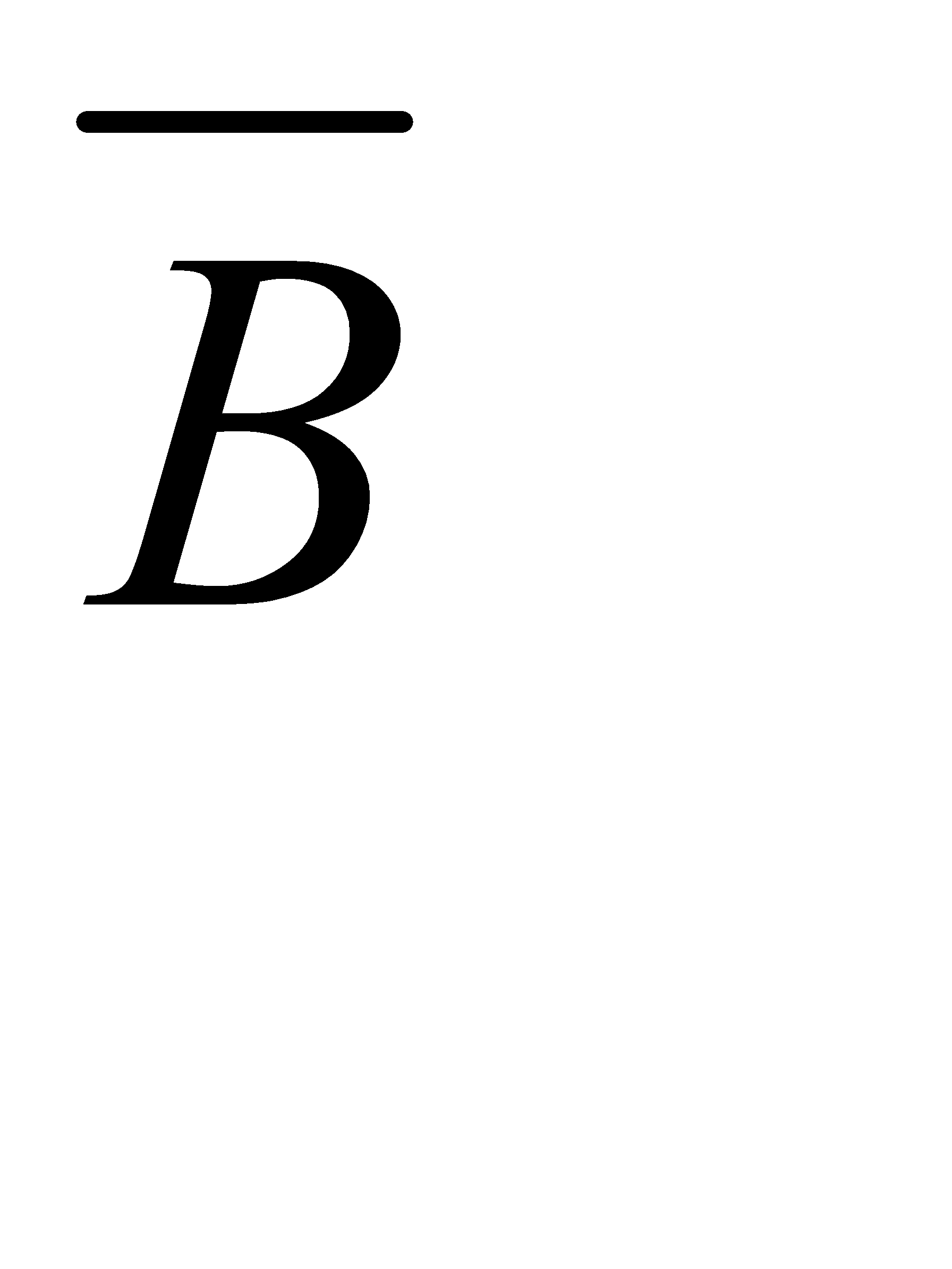 . По теореме сложения вероятностей несовместных событий получим
. По теореме сложения вероятностей несовместных событий получим
Р(А)= Р(АВ+ А 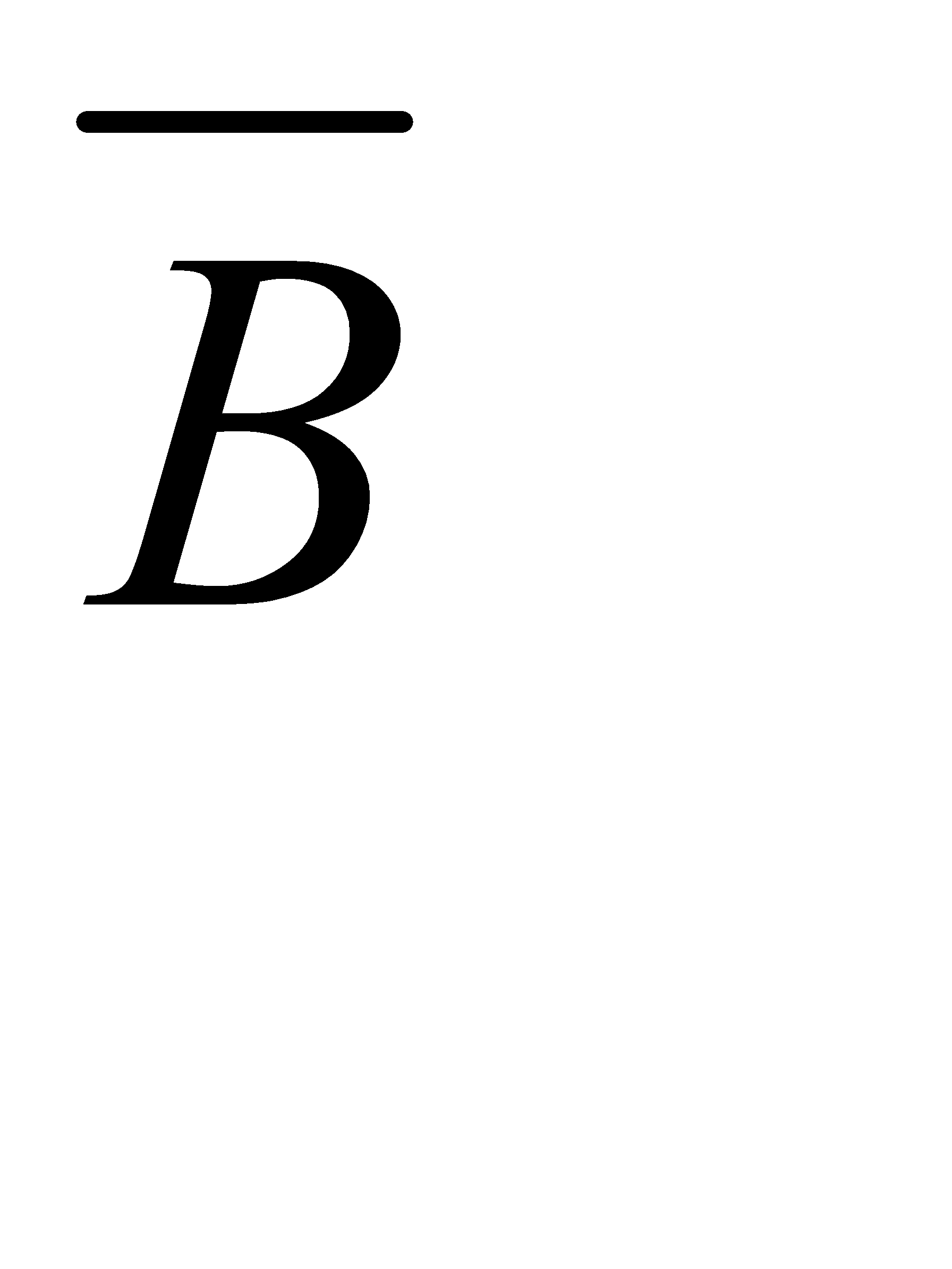 )=Р(АВ)+Р(А
)=Р(АВ)+Р(А 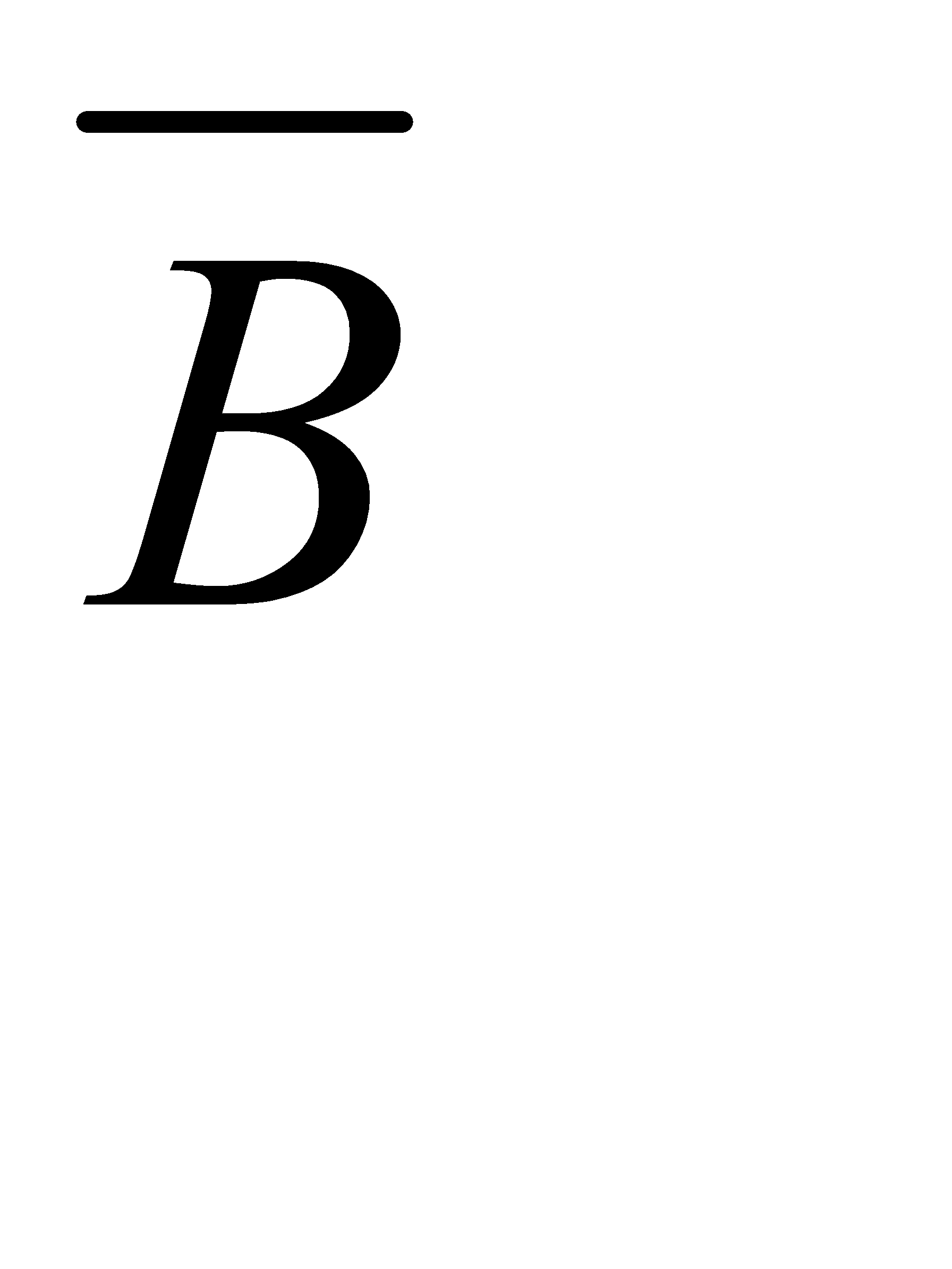 )=0, 72+0, 18=0, 9.
)=0, 72+0, 18=0, 9.
Ответ: 0, 9
#73 Найти вероятность 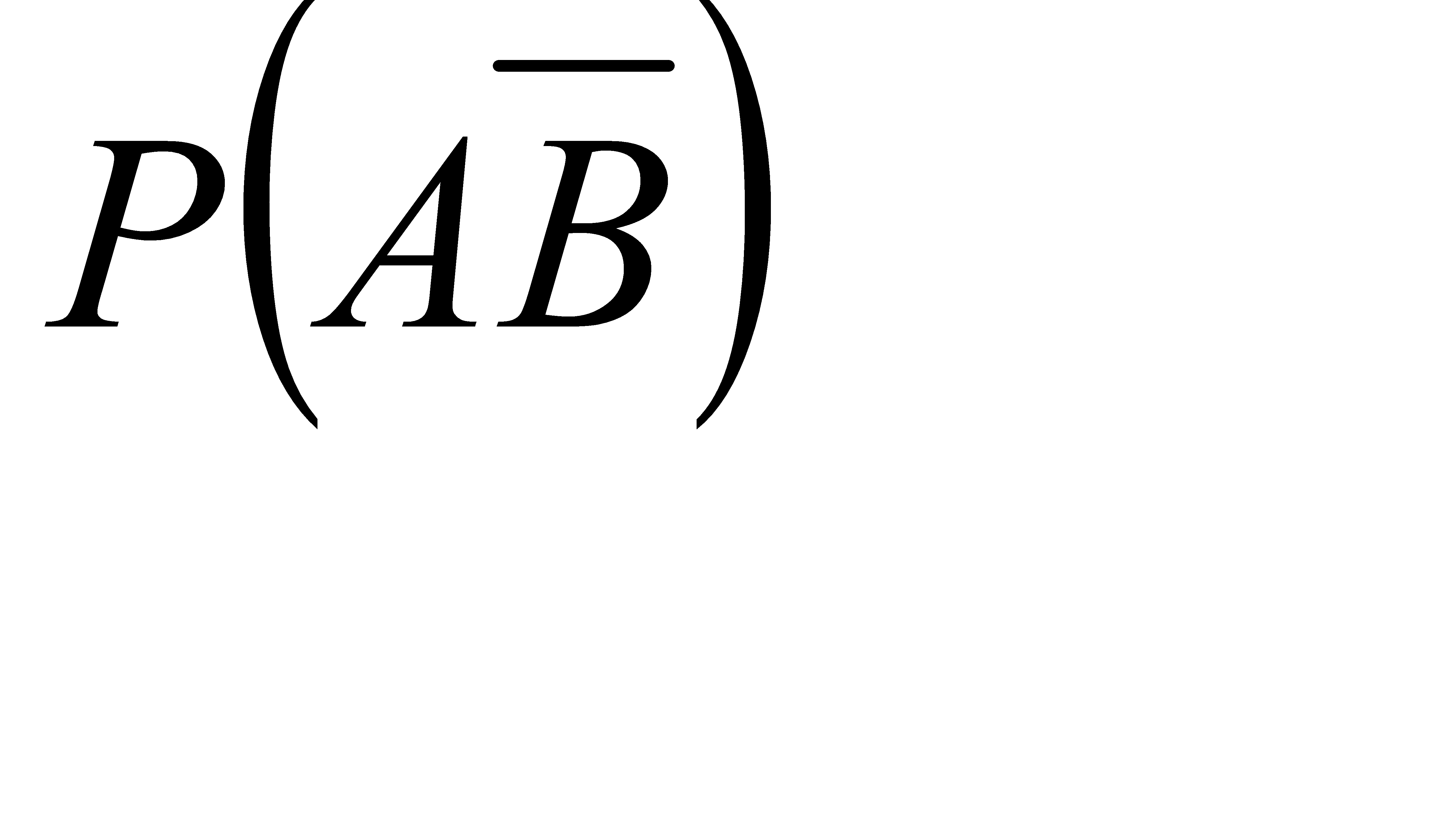 по данным вероятностям:
по данным вероятностям: 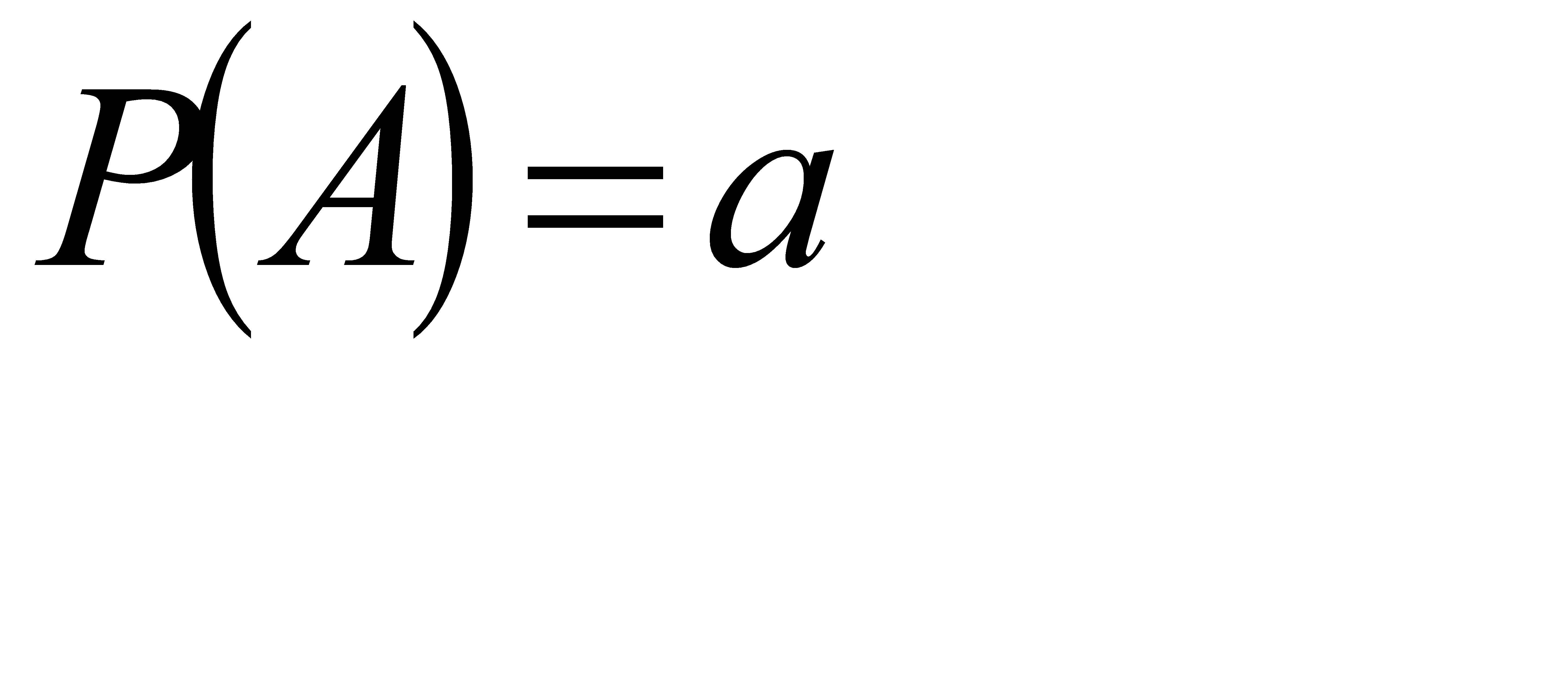 ,
, 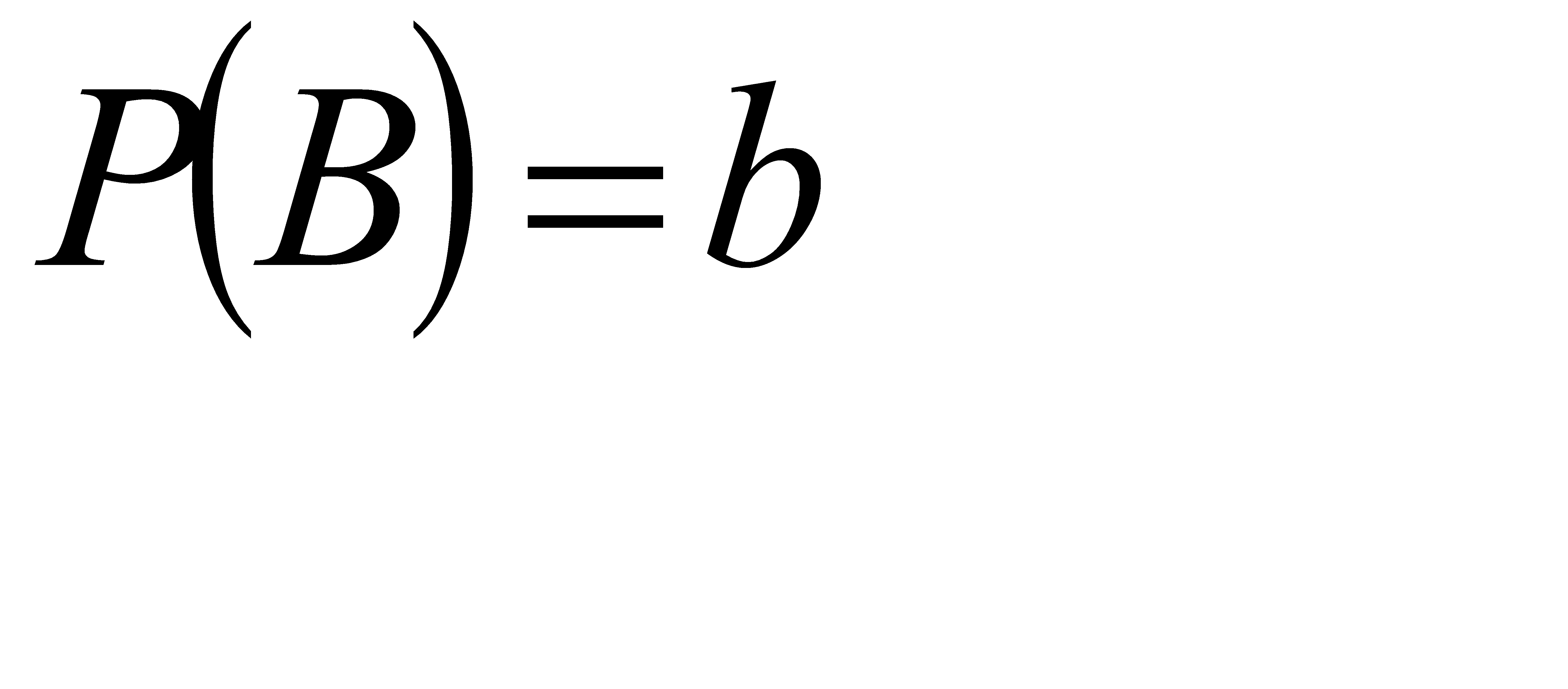 ,
, 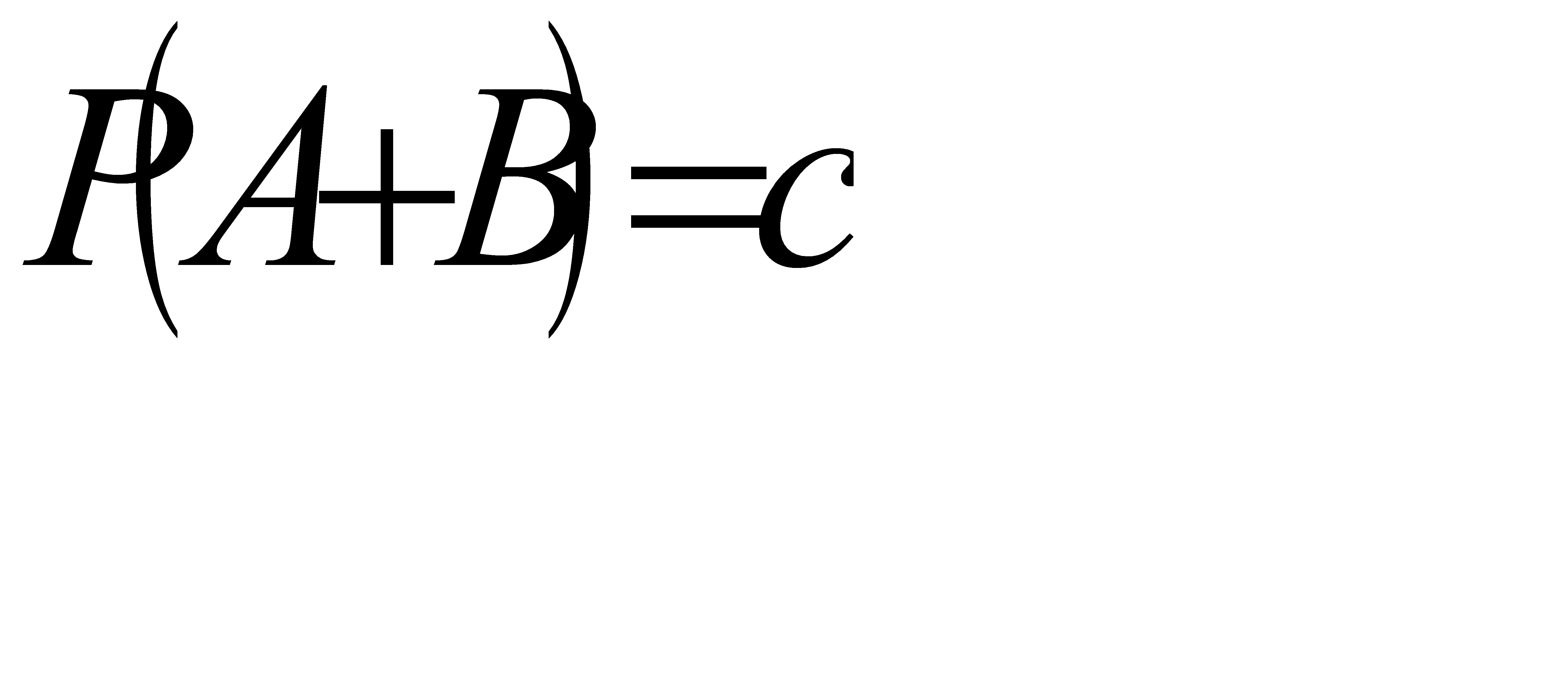 .
.
Решение. Используя тождество  найдём
найдём
 (*)
(*)
Из равенства  выразим
выразим 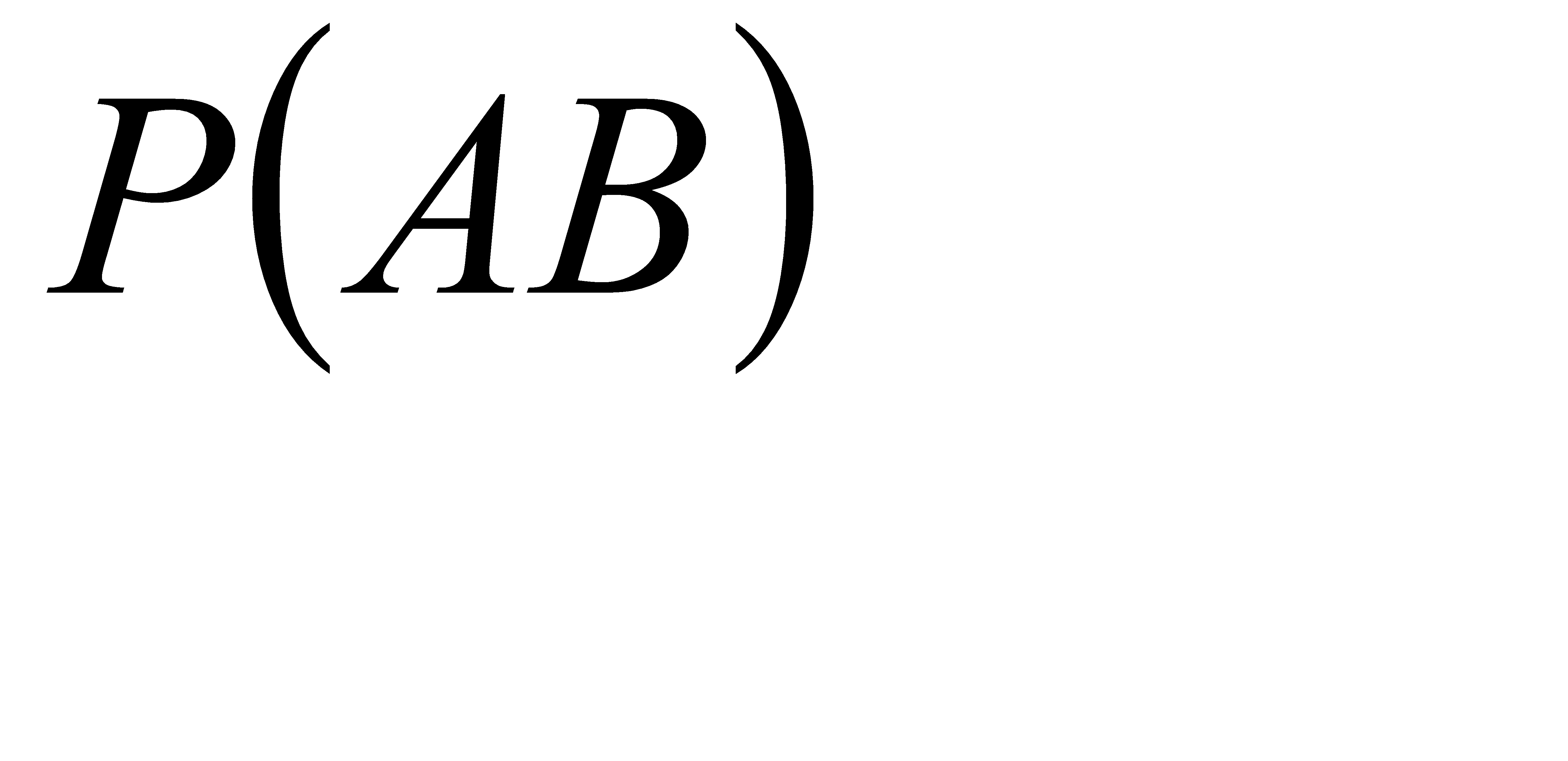 :
:
 (**)
(**)
Подставив (**) в (*), получим

#74 Задание: Найти вероятность 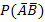 по данным вероятностям:
по данным вероятностям:
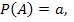
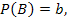
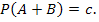 Решение: Используя тождество
Решение: Используя тождество 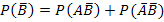 , найдем
, найдем 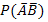 :
: 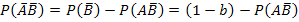
Подставив в последнее равенство 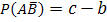 (см. задачу 73), получим:
(см. задачу 73), получим:
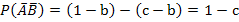 .
.
#75 Наступление события  необходимо влечёт наступление события
необходимо влечёт наступление события  . Доказать, что
. Доказать, что 
Решение: По условию, наступление события АВ влечёт наступление события  , поэтому.
, поэтому.  (*)
(*)
Используя тождества  ,
,  ,
, 
и учитывая неравенство (*), получим

#76 Доказать, что PA(B)≥ 1 - P(B)/P(A). Предполагается, что P(A)> 0.
Решение. Справедливо неравенство: P(A) + P(B) - P(AB) ≤ 1.
Воспользуемся тождествами: P(AB) = P(A)*PA(B), P(B) = 1 – P(B).
Подставив P(AB) = P(A)*PA(B), P(B) = 1 – P(B) в P(A) + P(B) - P(AB) ≤ 1,
получим P(A) + 1 – P(B) – P(A)*PA(B) ≤ 1, или
P(A)*PA(B) ≥ P(A) – P(B).
Разделив обе части неравенства на положительное число P(A), окончательно имеем:
PA(B) ≥ 1 - P(B) / P(A)
#77 По условию, наступление события 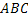 необходимо влечет наступление события
необходимо влечет наступление события  , следовательно (см. задачу 48),
, следовательно (см. задачу 48), 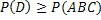 . Таким образом, если будет доказано неравенство
. Таким образом, если будет доказано неравенство 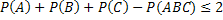 (*), то будет справедливо и неравенство, указанное в условии задачи.
(*), то будет справедливо и неравенство, указанное в условии задачи.
Докажем неравенство (*). Воспользуемся тождествами:
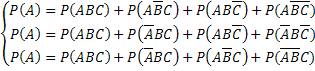 (**)
(**)
Из трех событий 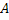 ,
, 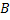 ,
, 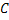 можно составить следующую полную группу «сложных событий», состоящих из появлений и непоявлений рассматриваемых трех событий:
можно составить следующую полную группу «сложных событий», состоящих из появлений и непоявлений рассматриваемых трех событий:
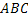 -появились все три события,
-появились все три события, 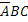 ,
, 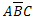 ,
, 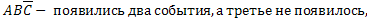
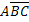 ,
, 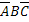 ,
, 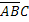 – появилось одно событие, а два других не появились,
– появилось одно событие, а два других не появились, 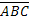 – не появились все три события.
– не появились все три события.
Сумма вероятностей событий, образующих полную группу, равна единице, поэтому 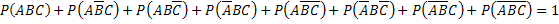
Отсюда 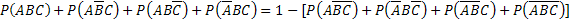 . (***)
. (***)
Подставив (**) в (*) и используя (***), после упрощений получим 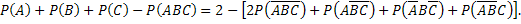
Учитывая, что каждое слагаемое в квадратной скобке неотрицательно, окончательно получим
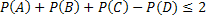 .
.
#78. Решение. Сведем сумму трех событий к сумме двух событий: А + В + С = (А + В) + С.
Воспользуемся теоремой сложения вероятностей двух событий:
Р(А + В + С) = Р[(А + В) + С] = Р(А + В) + Р(С) - Р[(А + В)*С] = Р(А + В) + Р(С) - Р[(А*С) + (В*С)]
Применим теорему сложения вероятностей двух совместных событий дважды (для событий А и В, а также для событий АС и ВС):
Р(А + В + С) = Р(А) + Р(В) – Р(АВ) + Р(С) - {Р(АС) + Р(ВС) – Р[(АС)(ВС)]}.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|