Таблица 1. Таблица 2. Таблица 3

Стр 1 из 2Следующая ⇒

Задано распределение двумерной случайной величины:

УIX 1 2 3

; 4 0, 1 0, 15 0, 12

5 0, 2 0, 22 0, 21.

распределения X имеет вид:

Какие из приведенных зависимостей являются законами распределения?

Таблица 1

УIX 1 2 3

; 4 0, 1 1, 5 0, 12

5 0, 2 0, 22 0, 1.

6 0, 01 0 0, 1

Таблица 2

УIX 1 2 3 5

; 4 0, 1 0, 15 0, 1 0, 02

5 0, 13 -0, 2 0, 15. 0, 05

6 0, 01 0, 03 0, 03 0, 04

Таблица 3

УIX 1 2 3

4 0, 42 0, 51 0, 15.

6 0, 1 0, 15 0, 1

8 0, 01 0, 03 0, 03

10 0, 05 0, 02 0, 04

Двумерную случайную величину обозначают через (X, У); каждая из величин X и Y называется... . ком

Законом распределения двумерной случайной величины (X, У) называют множество возможных пар чисел (х_i, у_j) и их вероятностей p(x_i, y_j)

Верно

закон распределения двумерной случайной величины (X, У) имеет вид прямоугольной таблицы из элементов p_ij, где p_ij=P(X=x_i: Y=y_j)

верно

Сумма всех вероятностей в законе распределения равна единице:

Верно

Из того, что Д(Х)+Д(У)¹ Д(Х+У) можно сделать вывод о том, что случайные величины являются независимыми.

Корреляционным моментом случайных величин X и У (или ковариацией) называется математическое ожидание произведений их отклонений:

ц_ху = Cov (X, У) = М{[Х - M(X)][Y -M(Y)]}

Корреляционный момент двух зависимых случайных величин X и Y равен нулю неверно

Коэффициентом корреляции случайных величин X и У называется отношение их ковариации ( корреляционного момента) к произведению средних квадратических отклонений этих величин:

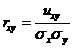
Верно

Коэффициент корреляции имеет свойство:

его абсолютная величина не превосходит единицы │ r_xy│ 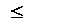1

Две случайные величины X и Y называются коррелированными, если их корреляционный момент (коэффициент корреляции) отличен от нуля

две коррелированные случайные величины (т. е. при г_ху № 0) являются также и зависимыми неверно

две зависимые величины могут быть как коррелированными, так и некоррелированными

верно

коэффициент корреляции близок к нулю; это означает, что случайные величины X и Y коррелированы.

Неверно

Линейная средняя квадратическая регрессия Y на X имеет вид

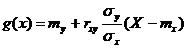
Верно

Коэффициент b = r_хуs_у/s_х называют коэффициентом регрессии Y на X

Верно

Сумма всех вероятностей в законе распределения равна нулю

Неверно

Две случайные величины X и Y называются коррелированными, если их корреляционный момент (коэффициент корреляции) равен нулю

Неверно

Законы распрелелднмия

медиана случайной величины X, имеющей равномерное распределение R(2; 8) равна:
5

Вероятность Р(Х. > 7) случайной величины X, имеющей равномерное распределение R(2; 8) равна:
1/6

Вероятность Р(Х. =7) случайной величины X, имеющей равномерное распределение R(2; 8) равна:
0

Вероятность Р(Х. > 10) случайной величины X, имеющей равномерное распределение R(2; 8) равна 0

Вероятность Р(Х< 1) случайной величины X, имеющей равномерное распределение R(2; 8) равна 0

Вероятность Р(3< Х< 7) случайной величины X, имеющей равномерное распределение R(2; 8) равна 2/3

математическое ожидание случайной величины X, имеющей равномерное распределение R(2; 8) равно 5

Функцией распределения случайной величины X называется функция F(x), определяющая вероятность того, что случайная величина X примет значение, меньшее х:

F(x) = Р(Х < х). верно

Случайная величина называется непрерывной, если ее функция распределения есть непрерывная кусочно-дифференцируемая функция с непрерывной производной. Верно

Производная от функции распределения непрерывной случайной величины X называется плотностью распределения вероятностей X:

f(x) = F'(x). Верно

Интеграл с переменным верзним пределом от плотности распределения вероятностей f(x) непрерывной случайной величины X называется функцией распределения F(x):

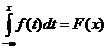верно

Вероятность того, что непрерывная случайная величина X не примет значение на интервале (а, b), определяется по формуле

Р(а < X < b) = 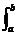f(x)dx=F(b)-F(a).

Верно

Функция распределения является неубывающей, т. е.

F(x₂) 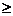F(x₁) при x₂> x₁

Верно

Область значений функции распределения лежит на отрезке [0, 1]:

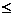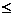О F(x) 1. верно

Если возможные значения случайной величины находятся на интервале (а, b), то F(x) = 0 при х< а и F(x) = 1 при х > b. верно

Вероятность того, что случайная величина X принимает значения, заключенные внутри интервала (а, b), равна разности значений функции распределения на концах этого интервала:

Р(а £ X< b)=F(b)- F(a).

Верно

Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю. Верно

Если возможные значения непрерывной случайной величины X расположены на всей числовой оси, то

lim F(x) = 0, lim F( x) = 1. верно

^x^®^-^¥ ^x^®¥

Плотность распределения не является неотрицательной функцией:

Невероно

Несобственный интеграл от плотности распределения в пределах интегрирования по всей числовой оси равен единице:

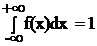верно

Математическим ожиданием непрерывной случайной величины X, называется определенный интеграл:

М(Х) = 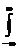xf(x)dx.

Верно

Дисперсией непрерывной случайной величины X называется математическое ожидание квадрата ее отклонения:

D(X) = 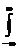{x - M(X)}²f(x)dx. Верно

Среднее квадратическое отклонение случайной величины определяется по формуле

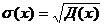
Верно

Классич опр вероя

Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее пяти очков, равна…

2/6

Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет «четверка», равна…1/6

Игральная кость бросается два раза. Тогда вероятность того, что на верхней грани оба раза выпадет «четверка», равна…1/36

Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани не выпадет «четверка», равна…5/6

Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее четырех очков, равна…1/2

Игральная кость бросается два раза. Тогда вероятность того, что на верхней грани оба раза не выпадет «тройка», равна…25/36

Бросают 2 монеты. События А - «герб на первой монете» и В - «цифра на второй монете» являютсяюю сомв и пезав

Бросают 2 игральные кости. События А - «шестерка на первой кости» и В - «двойка на второй кости» являются… совм и незав

Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет менее четырех очков, равна… ½

12 Следующая ⇒