
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Повтор Выход
ЧАСТЬ 2
Разработать алгоритм и программу вычисления корня уравнения f(x)=0 заданного на отрезке [A; B] методом дихотомии с допустимой погрешностью ε, равной: 0. 01, 0. 005, 0. 0005, 0. 002, 0. 00001.

Таблица данных:
| Название переменной | Тип | Структура | Смысл |
| Исходные данные: | |||
| A | real | Простая переменная | Левая граница |
| B | Правая граница | ||
| E | Массив | Допустимая погрешноть | |
| Результаты: | |||
| X | real | Простая переменная | Исходное значение с допустимой погрешностью |
| l | Integer | Количество итераций | |
| Промежуточные данные: | |||
| At | real | Простая переменная | Текущая левая граница |
| Bt | Текущая правая граница | ||
| St | Средняя точка | ||
| Fat | Знак функции в левой половине | ||
| Fst | Знак функции в средней точке | ||
| i | Integer | Счетчик цикла | |
Алгоритм:
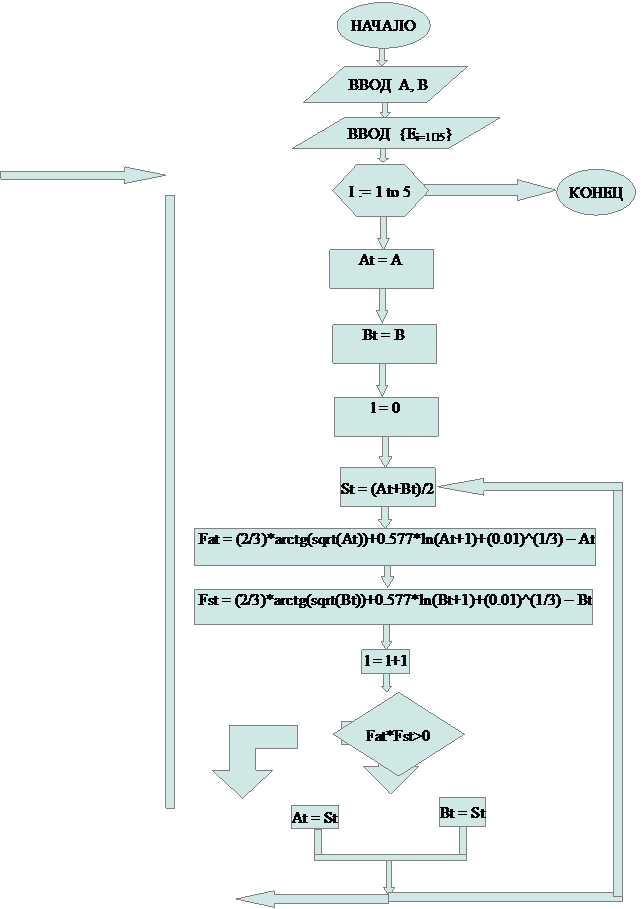
Повтор Выход
Да Нет
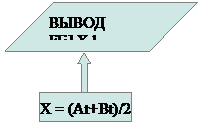 | |||
 | |||
Программа:
var E: array[1.. 5] of real;
A, B, At, Bt, St, fat, fst, x: real;
l, i: integer;
Begin
write('Input A, B: ');
read(A, B);
write('Input E[1.. 5]: ');
for i: = 1 to 5 do
read(E[i]);
writeln('Epsilon Root Iterations');
for i: = 1 to 5 do
begin
At: = A;
Bt: = B;
l: = 0;
repeat
st: = (At+Bt)/2;
fat: = (2/3)*arctan(sqrt(At))+0. 577*ln((At+1))+(0. 01/abs(0. 01)*exp((1/3)*ln(abs(0. 01)))) - At;
fst: = (2/3)*arctan(sqrt(Bt))+0. 577*ln((Bt+1))+(0. 01/abs(0. 01)*exp((1/3)*ln(abs(0. 01)))) – st;
l: =l+1;
if fat*fst > 0 then
At: = st
else Bt: = st;
until abs(Bt-At) < = E[i];
x: = (At+Bt)/2;
write(E[i]: 7: 5, ' ');
write(x: 10: 5, ' ');
writeln(l);
end;
readln;
end.
Тесты:
1. Тест 1
ñ Исходные данные:
◦ A =
◦ B =
◦ E = 0. 01 0. 05 0. 005 0. 002 0. 00001
ñ Результат:
| Epsilon | Root | Iterations |
| 0. 01 | ||
| 0. 005 | ||
| 0. 0005 | ||
| 0. 002 | ||
| 0. 00001 |
2. Тест 2
ñ Исходные данные:
◦ A =
◦ B =
◦ E = 0. 01 0. 05 0. 005 0. 002 0. 00001
ñ Результат:
| Epsilon | Root | Iterations |
| 0. 01 | ||
| 0. 005 | ||
| 0. 0005 | ||
| 0. 002 | ||
| 0. 00001 |
3. Тест 3
ñ Исходные данные:
◦ A =
◦ B =
◦ E = 0. 01 0. 05 0. 005 0. 002 0. 00001
ñ Результат:
| Epsilon | Root | Iterations |
| 0. 01 | ||
| 0. 005 | ||
| 0. 0005 | ||
| 0. 002 | ||
| 0. 00001 |
ЧАСТЬ 3
Разработать алгоритм и программу вычисления корня уравнения f(x)=0 заданного на отрезке [A; B] методом дихотомии с допустимой погрешностью ε, равной: 0. 01, 0. 005, 0. 0005, 0. 002, 0. 00001. Для вычисления корня уравнения и числа итераций при данном значении ε использовать подпрограмму-процедуру вместо внутреннего цикла.

Таблица данных процедуры Solve:
| Название переменной | Тип | Структура | Смысл |
| Входные формальные параметры: | |||
| A | real | Простая переменная | Левая граница |
| B | Правая граница | ||
| E | Допустимая погрешноть | ||
| Выходные формальные параметры: | |||
| X | real | Простая переменная | Исходное значение с допустимой погрешностью |
| l | Integer | Количество итераций | |
| Промежуточные данные: | |||
| At | real | Простая переменная | Текущая левая граница |
| Bt | Текущая правая граница | ||
| St | Средняя точка | ||
| Fat | Знак функции в левой половине | ||
| Fst | Знак функции в средней точке | ||
Таблица данных основной части программы:
| Название переменной | Тип | Структура | Смысл |
| Исходные данные: | |||
| A | real | Простая переменная | Левая граница |
| B | Правая граница | ||
| E | 1-мерный массив | Допустимая погрешноть | |
| Результаты: | |||
| X | real | Простая переменная | Исходное значение с допустимой погрешностью |
| l | Integer | Количество итераций | |
| Промежуточные данные: | |||
| i | Integer | Простая переменная | Счетчик цикла |
Блок-схема процедуры Solve:





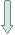

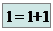



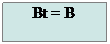

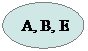
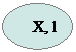
 |


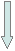

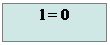
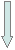


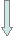



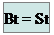
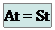
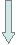

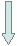





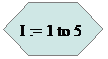



 Блок-схема основной части программы:
Блок-схема основной части программы:
 |
 |

 | |||
 | |||
Код:
var E: array[1.. 5] of real;
A, B, x: real;
l, i: integer;
Procedure Solve(A: real; B: real; E: real; var X: real; var l: integer);
var At, Bt, St, Fat, Fst: real;
begin
At: = A;
Bt: = B;
l: = 0;
repeat
st: = (At+Bt)/2;
Fat: = (2/3)*arctan(sqrt(At)) + 0. 577*ln(At+1) + (0. 01/abs(0. 01)*exp((1/3)*ln(abs(0. 01)))) - At;
Fst: = (2/3)*arctan(sqrt(St)) + 0. 577*ln(St+1) + (0. 01/abs(0. 01)*exp((1/3)*ln(abs(0. 01)))) - St;
if Fat*Fst > 0 then
At: = St
else
Bt: = St;
l: = l+1;
until abs(Bt-At) < = E;
X: = (At+Bt)/2;
end;
begin
write('Input A, B: ');
read(A, B);
write('Input E[1.. 5]: ');
for i: = 1 to 5 do
read(E[i]);
writeln('Epsilon Root Iterations');
for i: = 1 to 5 do
begin
Solve(A, B, E[i], x, l);
write(E[i]: 7: 5, ' ');
write(x: 10: 5, ' ');
writeln(l);
end;
readln;
end.
Тесты:
1. Тест 1
ñ Исходные данные:
◦ A =
◦ B =
◦ E = 0. 01 0. 05 0. 005 0. 002 0. 00001
ñ Результат:
| Epsilon | Root | Iterations |
| 0. 01 | ||
| 0. 005 | ||
| 0. 0005 | ||
| 0. 002 | ||
| 0. 00001 |
2. Тест 2
ñ Исходные данные:
◦ A =
◦ B =
◦ E = 0. 01 0. 05 0. 005 0. 002 0. 00001
ñ Результат:
| Epsilon | Root | Iterations |
| 0. 01 | ||
| 0. 005 | ||
| 0. 0005 | ||
| 0. 002 | ||
| 0. 00001 |
3. Тест 3
ñ Исходные данные:
◦ A =
◦ B =
◦ E = 0. 01 0. 05 0. 005 0. 002 0. 00001
ñ Результат:
| Epsilon | Root | Iterations |
| 0. 01 | ||
| 0. 005 | ||
| 0. 0005 | ||
| 0. 002 | ||
| 0. 00001 |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|