
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример.. Пример.. Решение.. 1.6.2. Композиция функций
Пример.
Отношение f = {(x, y)| y = x2, x, y Î R} – функция. Но обратное отношение 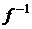 = {(x, y)| x = y 2} уже функцией не является, ему, например, принадлежат пары (9, 3) и (9, -3).
= {(x, y)| x = y 2} уже функцией не является, ему, например, принадлежат пары (9, 3) и (9, -3).
Чтобы условие однозначности выполнялось для отношения 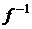 , функция
, функция 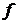 должна быть, очевидно, инъективной.
должна быть, очевидно, инъективной.
Утверждение.
Пусть 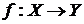 - тотальная биекция, тогда отношение
- тотальная биекция, тогда отношение 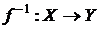 также является тотальной биекцией.
также является тотальной биекцией.
Доказательство.
1. Докажем, что 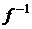 - функция.
- функция.
Пусть 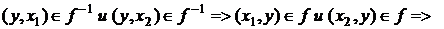
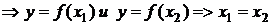 , т. к. функция f – инъекция (у каждого образа y есть единственный прообраз x).
, т. к. функция f – инъекция (у каждого образа y есть единственный прообраз x).
2. 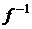 – тотальна,
– тотальна, 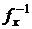 = Y, т. к. f – сюръекция.
= Y, т. к. f – сюръекция.
3. 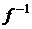 – сюръекция,
– сюръекция, 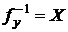 т. к. f – тотальна.
т. к. f – тотальна.
Итак, если f – тотальная биекция, то все элементы множества X – прообразы (тотальность), а все элементы множества Y – образы (сюръекция). Тогда, по определению 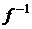 , все элементы множества Y становятся прообразами (тотальность), а элементы множества X становятся образами (сюръективность).
, все элементы множества Y становятся прообразами (тотальность), а элементы множества X становятся образами (сюръективность).
4. Докажем, что 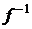 – инъекция. Допустим, что это не так,
– инъекция. Допустим, что это не так, 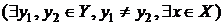 :
: 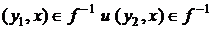 . Но тогда
. Но тогда 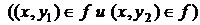 - противоречие, так как f – функция.
- противоречие, так как f – функция.
Пример.
Функция 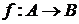 задана формулой: f (x) = 1+2/x, где A = R\{0}, B = R\{1}.
задана формулой: f (x) = 1+2/x, где A = R\{0}, B = R\{1}.
Показать, что f – тотальная биекция и найти 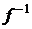 .
.
Решение.
Возьмем х 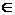 R\{0}. По этому значению х однозначно определяется у = =1+2/x. Следовательно, f – тотальная функция.
R\{0}. По этому значению х однозначно определяется у = =1+2/x. Следовательно, f – тотальная функция.
Покажем, что f – биекция. Возьмем у 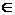 R\{1}. Определим х по этому значению у, у = 1+2/x Þ х = 2/(у - 1). Значение х вычисляется однозначно, f – тотальная биекция.
R\{1}. Определим х по этому значению у, у = 1+2/x Þ х = 2/(у - 1). Значение х вычисляется однозначно, f – тотальная биекция.
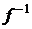 = {(у, х)| y = 1+2/x, x, y Î R,
= {(у, х)| y = 1+2/x, x, y Î R, 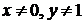 } =
} =
= {(х, у)| y = 2/(х - 1), x, y Î R, 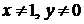 }.
}.
Пусть AÍ X, тогда по определению 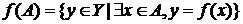 . Множество
. Множество 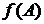 называется образом множества А.
называется образом множества А.
Пусть BÍ Y, тогда по определению 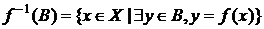 . Множество
. Множество 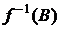 называется прообразом множества В.
называется прообразом множества В.
Пример .
Положим у = х2. Найти образы множеств [0; 1]; [-2; 1); [-2; 2);
(-3; -1. 5) 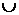 (0; 2).
(0; 2).
Найти прообразы множеств [0; 1]; [1; 4]; [0, 01; 0, 25].
Решение. f([0; 1]) = [0; 1]; f([-2; 1)) = [0; 4]; f([-2; 2)) = [0; 4]; f((-3; -1, 5) 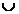 (0, 2)) = (0; 9);
(0, 2)) = (0; 9); 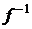 ([0; 1]) = [-1; 1];
([0; 1]) = [-1; 1]; 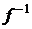 ([1; 4]) = [-2; -1]
([1; 4]) = [-2; -1] 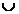 [1; 2];
[1; 2]; 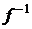 ([0, 01; 0, 25]) = [-0, 5; -0, 1]
([0, 01; 0, 25]) = [-0, 5; -0, 1] 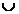 [0, 1; 0, 5].
[0, 1; 0, 5].
1. 6. 2. Композиция функций
Так как всякая функция – это бинарное отношение, можно строить композицию функций, как композицию бинарных отношений.
Если f: X® Z (z = f(x)) и g: Z® Y (y = g(z)), их композиция f  g определяется обычным образом,
g определяется обычным образом,
f  g = {(x, y)| xÎ X, yÎ Y, (
g = {(x, y)| xÎ X, yÎ Y, ( 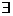 zÎ Z): (x, z)Î f и (z, y)Î g}.
zÎ Z): (x, z)Î f и (z, y)Î g}.
Учитывая, что f и g – функции, можно записать f  g = {(x, y)| xÎ X, yÎ Y, (
g = {(x, y)| xÎ X, yÎ Y, ( 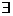 zÎ Z): (x, z)Î f и (z, y)Î g} = {(x, y)| (
zÎ Z): (x, z)Î f и (z, y)Î g} = {(x, y)| ( 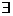 z): z = f(x)и y = g(z)} = {(x, y)| y = g(f(x))}.
z): z = f(x)и y = g(z)} = {(x, y)| y = g(f(x))}.
Теперь видно, что композиция функций – не просто бинарное отношение, а тоже функция, отображающая множество Х в множество Y.
Пример.
Пусть f(x) = 2x + 1, g(x) = 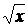 .
.
Найти f  g, g
g, g 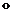 f и f
f и f 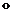 f. Указать области определения и области значений этих функций.
f. Указать области определения и области значений этих функций.
Решение .
(f  g)(x) = g(f(x)) =
g)(x) = g(f(x)) = 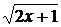 ,
, 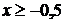 , (f
, (f  g)(x) ³ 0;
g)(x) ³ 0;
(g 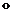 f)(x) = f(g(x)) = 2
f)(x) = f(g(x)) = 2 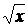 +1,
+1, 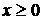 , (g
, (g 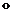 f)(x) ³ 1.
f)(x) ³ 1.
Композиция - некоммутативная операция,
f 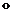 g(x)≠ g
g(x)≠ g 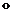 f(x).
f(x).
Покажем, что для композиции справедлив закон ассоциативности.
Пусть f, g, h - три функции с согласованными областями определений и значений, так что их композицию можно найти. Тогда
(f  g)
g)  h(x) = h(f
h(x) = h(f  g(x)) = h(g(f(x)))
g(x)) = h(g(f(x)))
f  (g
(g  h)(x)= (g
h)(x)= (g  h)(f(x)) = h(g(f(x)))
h)(f(x)) = h(g(f(x)))
Закон ассоциативности справедлив для любого числа функций. Та единственная функция, которая есть результат композиции функций f1, f2, f3, …, fn (в указанном порядке), так и обозначается:
f1  f2
f2  f3
f3  …
…  fn.
fn.
Пример.
Найти все композиции функций f1 = x2, f2 = sin(x), f3 = x3 – 1
f1  f2
f2  f3 = (sin(x2))3– 1, f1
f3 = (sin(x2))3– 1, f1  f3
f3  f2 = sin(x6 – 1), f2
f2 = sin(x6 – 1), f2  f1
f1  f3 = sin6(x) – 1,
f3 = sin6(x) – 1,
f2  f3
f3  f1 = (sin3(x)-1)2, f3
f1 = (sin3(x)-1)2, f3  f1
f1  f2 = sin(x3 – 1)2, f3
f2 = sin(x3 – 1)2, f3  f2
f2  f1 = sin2(x3 – 1).
f1 = sin2(x3 – 1).
Положим теперь, что f и g - биекции. Если z = f(x), то
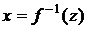 – биекция. Если y = g(z), то z =
– биекция. Если y = g(z), то z = 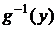 – биекция. Выясним, какими свойствами обладает композиция биекций.
– биекция. Выясним, какими свойствами обладает композиция биекций.
Утверждение.
Композиция взаимно однозначных функций – взаимно однозначная функция, при этом 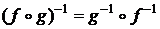 .
.
Доказательство.
1. 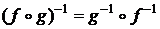 в силу доказанного в лекции 1. 4 свойства композиции всяких бинарных от ношений.
в силу доказанного в лекции 1. 4 свойства композиции всяких бинарных от ношений.
2. Допустим, что 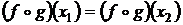 . Тогда g(f(x1)) = g(f(x2)) = y. В силувзаимной однозначности функции g f(x1) = f(x2). В силу взаимной однозначности функции f x1 = x2.
. Тогда g(f(x1)) = g(f(x2)) = y. В силувзаимной однозначности функции g f(x1) = f(x2). В силу взаимной однозначности функции f x1 = x2.
В заключение приведем ещё несколько примеров решения задач.
Пример 1. Пусть Х, Y – два множества, состоящие из n и m элементов соответственно. Какова мощность множества всех тотальных функций, определенных на Х, со значениями в Y?
Решение. Чтобы задать любую тотальную функцию нужно выполнить одно за другим и независимо одно от другого n действий: указать образ каждого элемента множества Х. Но каждое действие можно выполнить m способами Þ число функций равно mn.
Пример 2. Доказать, что 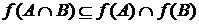 , где f – произвольная функция, и что равенство получается, когда
, где f – произвольная функция, и что равенство получается, когда 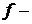 инъекция. Привести пример строгого включения.
инъекция. Привести пример строгого включения.
Решение .
1. 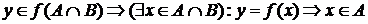 и
и 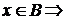
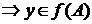 и
и 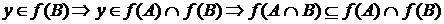 .
.
2. Если 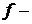 инъекция, условие однозначности выполнено также и для значений функции
инъекция, условие однозначности выполнено также и для значений функции 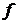 , по каждому значению
, по каждому значению 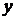 однозначно определяется аргумент
однозначно определяется аргумент 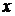 , значение которого равно
, значение которого равно 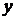 .
.
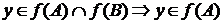 ,
, 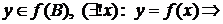
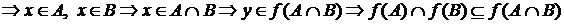 ,
, 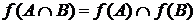 .
.
3. Если 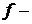 не инъекция, то множества
не инъекция, то множества 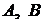 аргументов могут вообще не пересекаться, а множества
аргументов могут вообще не пересекаться, а множества 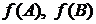 значений могут иметь не пустое пересечение. Положим
значений могут иметь не пустое пересечение. Положим 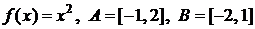 . Тогда
. Тогда 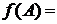
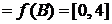 ,
,  ,
, 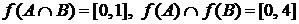 ,
,
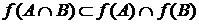 .
.
Пример 3. Доказать, что 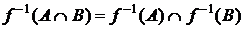 .
.
Решение .
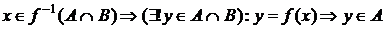 ,
,
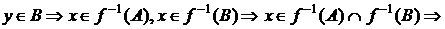 ,
, 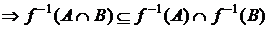 .
.
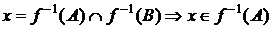 ,
, 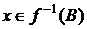 и
и 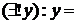
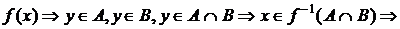

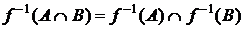 .
.
Замечание. Запись 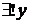 читается так: существует и единственен элемент
читается так: существует и единственен элемент 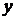 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|