ДО 4 БАЛЛОВ ЗА КОНСПЕКТ. Функции. 1.6.1. Определение функции. Областью определения функции f называют множество ее аргументов (прообразов), . Если область определения совпадает с Х, то функция называется тотальной, в противном случае функция называется ч

ДО 4 БАЛЛОВ ЗА КОНСПЕКТ

Функции

1. 6. 1. Определение функции

Определение. Функцией называют бинарное отношение 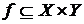, обладающее следующим свойством: если и 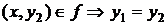. Это означает, что если определён первый элемент упорядоченной пары, то второй элемент определяется единственным образом.

Такое свойство функции называют однозначностью . Говорятеще, чтодля функции выполнено условие однозначности. Обозначения функции: 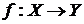, , 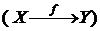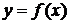. Функция f отображает множество 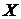в множество Y.

Если y = f(x), то элемент x из множества Х называют аргументом функции или прообразом элемента y, а элемент y – значением функции или образом элемента x.

В силу условия однозначности у всякого прообраза есть единственный образ.

Аргументы функции - элементы произвольной природы. В частности, они могут быть упорядоченными энками, 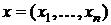. В этом случае функцию 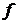называют функцией 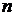переменных и пишут: 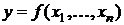. Функция двух переменных 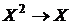в некоторых случаях называется бинарной операцией.

Областью определения функции f называют множество ее аргументов (прообразов), . Если область определения совпадает с Х, то функция называется тотальной, в противном случае функция называется частично определенной.

Областью значений 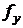функции f называют множество ее значений (образов), 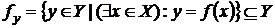Если область значений совпадает с множеством Y, функция называется сюръекцией или сюръективной.

О сюръективной функции говорят, что она отображает множество Х на множество Y.

Пример.

Определить, какие из приведенных бинарных отношений являются функциями.

1. {(1, 1), (1, 2), (2, 4), (3, 6)}; 2. {(1, 1), (2, 4), (3, 4)};

3. {(x, y)| x = y², x, y Î R}; 4. {(x, y)| y = x², x, y Î R}.

Решение .

1. Это бинарное отношение, не функция, нарушено условие однозначности. В бинарное отношение входят две разные упорядоченные пары – (1, 2) и (1, 1) с одинаковым первым элементом.

2. Данное бинарное отношение – функция с областью определения    {1, 2, 3} и множеством значений {1, 4}.

3. Отношение {(x, y)| x = y², x, y Î R} функцией не является. В него входят, например, упорядоченные пары (4, 2) и (4, -2).

4. Задана функция y = x². Значение у единственным образом определяется по значению аргумента х.

Определение. Функция 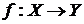называется инъективной или инъекцией, если 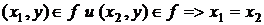. Другими словами, у каждого образа есть единственный прообраз.

Определение. Функция 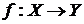называется биективной или биекцией, если она одновременно инъективна и сюръективна. Биекцию по-другому называют взаимно однозначным соответствием между областью определения и областью значений; каждому элементу x из области определения функция f ставит в соответствие единственный элемент y из области значений и наоборот, для каждого yÎ Y существует единственный xÎ X.

Проиллюстрируем введенные определения.



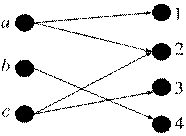
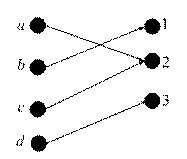
    Рис. 1. Бинарное отношение,             Рис. 2. Сюръекция, но не

                     но не функция                                 инъекция



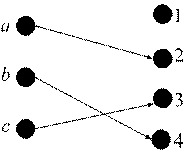
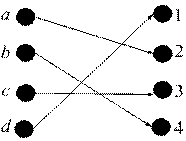
        Рис. 3. Инъекция, но не              Рис. 4. Тотальная биекция

                    сюръекция

Так как функция – это бинарное отношение, можно построить обратное бинарное отношение 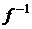, которое не обязательно является функцией. Условие однозначности может быть нарушено.

12 Следующая ⇒