
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
1. Похідна степеневої функції.
ПРАКТИЧНЕ ЗАНЯТТЯ №5
| Дисципліна: | «Математичний аналіз» | ||||
| Модуль | Модуль КЗН. 02. 03 Диференційне числення функції однієї та декількох змінних | ||||
| Модульна одиниця: | Похідна степеневої, показникової та складної показникової функції при будь-якому дійсному показнику. | ||||
План:
1. Похідна степеневої функції.
2. Похідна показникової функції, складної показникової та степенево-показникової.
3. Логарифмічне диференціювання.
1. Похідна степеневої функції.
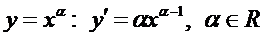 .
.
□ Диференціальне відношення (1) має такий вигляд:
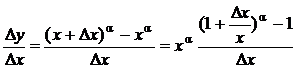 .
.
Згідно з одним із наслідків особливих границь, маємо:
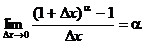 .
.
Отже, 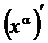 =
= 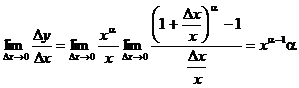 ■
■
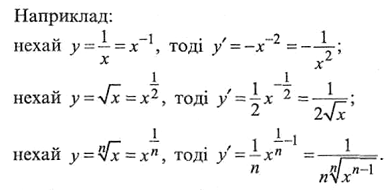
Приклади. Знайти похідні заданих функцій:
1) 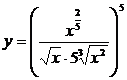 ; 2)
; 2) 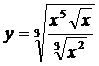 ; 3)
; 3) 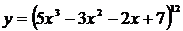 .
. 
□ 2) 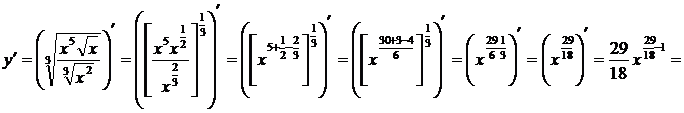
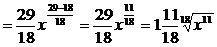 . ■
. ■
2. Похідна показникової функції, складної показникової та степенево-показникової.
Озн. Функція 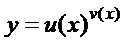 називається показниково-степеневою функцією.
називається показниково-степеневою функцією.
Окремі випадки:
1. Нехай функція y = f(x) є показниковою: 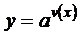 , тобто
, тобто 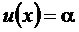 .
.
Тоді
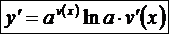 .
.
2. Нехай функція у = f(x) є степеневою, , тобто v(x) = a.
Тоді
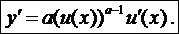
Приклади. Знайти похідні заданих функцій:
1) 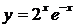 ; 2)
; 2) 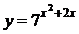 3)
3) 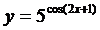 ; 4)
; 4)  .
.
□ 1) 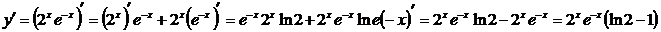 ■
■
□ 2) 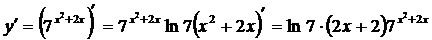 ■
■
□ 3) 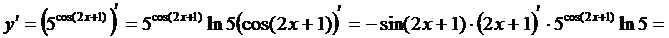
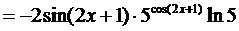 ■
■
□ 4) 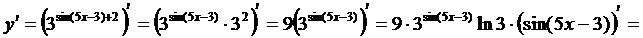
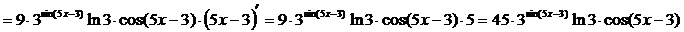 ■
■
Як знаходять похідну показниково-степеневої функції:
прологарифмуємо рівняння
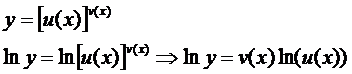

Продиференціюємо обидві частини останнього рівняння:
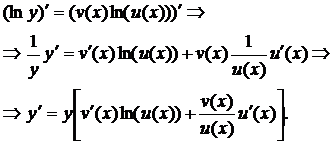
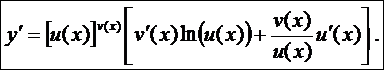
Правило диференціювання показниково-степеневої функції:
Щоб знайти похідну показниково-степеневої функції, потрібно спочатку продиференціювати її як показникову, а потім як степеневу функцію. Результати додати.
Приклади. 1) Знайти у¢, якщо у = х-tgx.
2) Знайти у¢, якщо у = (х2 + 1)sinx.
□ а) 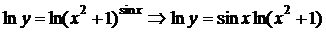 .
.
б) 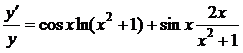 .
.
в) 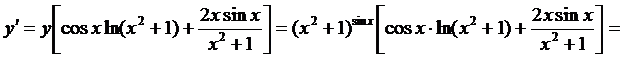

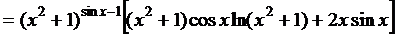 . ■
. ■
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|