
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Показники ЧСС до розминки та алгоритм їх статистичної обробки. Таблиця 1.
Показники ЧСС до розминки та алгоритм їх статистичної обробки. Таблиця 1.
| № з/п | xі | nі | xі nі | xі – x* | (xі – x*)2 | (xі – x*)2 nі |
| -7 -3 -1 | ||||||
| Всього | - | - | - |
Х* = 2832: 3018 = 157, 3 ~ 157 уд ● хв-1 ; S2x = 192: 18 ~ 10, 66 (уд ● хв-1)2;
Sx = 10, 66 ~ 3, 26 уд ● хв-1
Таким чином, до розминки показники групи складали Х* ± Sx = 157 ± 3, 0 уд ● хв-1.
Показники ЧСС після розминки та алгоритм їх статистичної обробки. Таблиця 2.
| № з/п | yі | nі | yі nі | yі – y* | (yі – y*)2 | (yі – y*)2 nі |
| -5 -3 | ||||||
| Всього | - | - | - |
Y*= 3042: 18 = 169 уд ● хв-1 ; S2y = 148: 18 ~ 8, 22 (уд ● хв-1)2;
Sy = 8, 22 ~ 2, 87 ~3, 0 уд ● хв-1
Відповідно, після розминки показники групи склали: Y* ± Sy = 169 ± 3, 0 уд ● хв-1.
Тепер визначимо дві помилки репрезентації. За умови невідомої генеральної сукупності і малого об`єму вибірки (n < 20) для визначення помилки використовуємо формулу:
mx = Sx / n – 1 = 3/ 18-1 = 3: 4, 12 = 0, 73 уд ● хв-1.
my = Sy / n – 1 = 3/ 18-1 = 3: 4, 12 = 0, 73 уд ● хв-1.
Помилки по двох групах співпали в зв`язку з тим, що об`єми вибірки рівні (досліджувалась одна й та сама группа за різних умов), а середнє квадратичне відхилення склало Sx = Sy = 3, 0 уд ● хв-1.
Переходимо до визначення критерію Стьюдента:
t = | x*1 - x*2 |: m21 + m22 = | x* - y* |: m2x + m2y = |157-169|: 0, 732 + 0, 732 = 11, 62.
Задаємо мінімальну надійність розрахунку: p = 0, 95. Кількість ступенів свободи k = n1 + n2 – 2 = 18+18-2 = 34. За таблицею знаходимо tкр = 2, 03. Звідси статистичний висновок такий: 11, 62 > 2, 03, тобто t > tкр. В цьому випадку різниця між вибірками статистично достовірна. Для даного випадку можуть розглядатись також інші (більш високі) ступені надійності (наприклад, p = 0, 999). На цьому рівні також підтверджується значимість відмінностей 2-х середніх величин: 11, 62 > 3, 60 (p < 0, 001). Таким чином за показниками ЧСС можна стверджувати, що розминка є ефективною.
Критерій Фішера. Якщо потрібно перевірити гіпотезу про те, що 2 незалежні вибірки, які одержані від 2-х генеральних сукупностей, відрізняються одна від одної, використовують F-критерій Фішера. Умови застосування цього критерія наступні: 2 вибірки повинні бути незалежними; вибірки повинні бути одержані від двох генеральних сукупностей з нормальним розподілом. Критерій Фішера знаходять за формулою:
F = S21 : S22
де S21 і S22 – дисперсії порівнюваних вибірок.
Умовами критерію Фішера передбачено, що в чисельнику формули знаходиться більша дисперсія, тобто значення коефіцієнта F завжди більше одиниці.
Наступний алгоритм підрахунку такий. Визначаємо надійність підрахунку: р = 0, 95 і визначаємо число ступенів свободи для обох вибірок – k1 = n1 -1; k2 = n2 -1. За таблицею знаходимо критичне значення критерію Fкр. Порівнюючи критерій F і Fкр, можна сформулювати висновки: якщо F ≥ Fкр, то різниця між двома вибірками достовірна; якщо F < Fкр – різниця статистично недостовірна.
Непараметричні методи порівняння вибірок засновані на рангових (порядкових) відмінностях між елементами вибірок. Ці методи значно простіші в розрахунках, ніж їх параметричні аналоги. При вирішенні питання вибору параметричних або непараметричних методів порівняння необхідно мати на увазі, що параметричні методи мають значно більшу статистичну чутливість, ніж непараметричні.
Умови, при яких застосування непараметричних методів - виправдане:
● вважають, що розподіл значень ознак в генеральній сукупності не відповідають нормальному розподілу;
● є сумнів щодо нормальності розподілу ознаки в генеральній сукупності, але вибірка достатньо мала, щоб за вибірковим розподілом робити висновки про генеральну сукупність;
● не виконується вимога гомогенності дисперсії при порівнянні середніх значень для незалежних вибірок.
Розглянемо наступні методи: критерії Вілкоксона, Уайта, Ван-дер-Вардена (критерій знаків).
Критерій Вілкоксона (W) є найчутливішим аналогом критерію t –Стьюдента для вибірок однакового об`єму при попарному порівнянні їх елементів. Він передбачає упорядкування величин різниці (зрушень) значень ознаки в кожній парі і визначається так:
1. Задаємо надійність підрахунку і визначаємо кількість ступенів свободи (k = n -1, де n – кількість пар елементів обох груп). За таблицею знаходимо критичні значення Wкр.
2. Порівняння критеріїв W і Wкр. дозволяє зробити висновки:
якщо W ≥ Wкр, то різниця між двома вибірками статистично недосто-вірна; якщо W < Wкр – різниця статистично достовірна.
За допомогою Критерію Уайта ( Т ) порівнюють 2 різні за об`ємом, але невеликі вибірки. Цей критерій визначають таким чином:
1. Задаємо надійність підрахунку при двох об`ємах вибірки n1 і n2.
2. За таблицею Уайта знаходимо величину критичного значення (Ткр).
3. Порівняння критеріїв Т і Ткр дозволяє зробити висновки: якщо Т ≥ Ткр, то різниця між порівнюваними групами статистично недосто-вірна; якщо Т < Ткр – різниця статистично достовірна.
Критерій Ван-дер-Вардена (критерій знаків) призначений для переведення попарного альтернативного порівняння і застосовується для вибірок значного об`єму. Послідовність використання цього критерію.
1. Порівняємо попарно елементи вибірок і визначимо кожній парі відповідний знак: «+» у випадку покращення ознаки, «-» - погіршен-ня, «)» - без зміни.
2. Задамо надійність р = 0, 95 при кількості порівнюваних пар, наведе-них в умовах завдання (без врахування нульових пар); за таблицею Ван-дер-Вардена визначимо критичні значення критерю zкр, який представляє собою певний інтервал, що обмежений нижнім числом а і верхнім числом в (zкр =[a…в]).
3. Порівняння ознак двох статистичних рядів дозволяє зробити висновки: якщо додатній (+) або від`ємний (-) знак залежно від умов завдання входить в інтервал, різниця між вибірками – статистично недостовірна; якщо вони виходять за межі інтервалу – різниця достовірна.
Взаємозв`язок результатів вимірювань. В дослідженнях у ФВС дуже часто стоїть завдання визначення взаємоз`язку між декількома ознаками (наприклад, розвитком швидкісних здібностей і результатом стрибків у довжину). Існують три способи аналізу щільності взаємозв`язку: функціональний, статистичний і кореляційний.
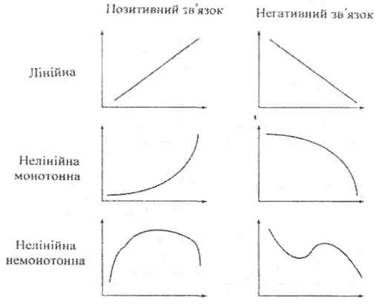 Функціональний зв`язок – це залежність, за якої кожному значенню одного показника відповідає чітко визначене значення іншого. Приклади ймовірного функціонального зв`язку наведені на Рис. 1.
Функціональний зв`язок – це залежність, за якої кожному значенню одного показника відповідає чітко визначене значення іншого. Приклади ймовірного функціонального зв`язку наведені на Рис. 1.
Рис. 1. Приклади графіків функцій, які часто зустрічаються
Якщо змінюваність однієї змінної на одну одиницю завжди приводить до змінюваності іншої змінної на одну й ту саму величину, то функція є лінійною. Інший зв`язок – нелінійний. Якщо збільшення однієї змінної пов`язано із збільшенням іншої, то зв`язок додатній (прямий), а якщо – із зменшенням іншої, то зв`язок від`ємний (зворотний). Якщо напрям зміни однієї змінної не міняється із зростанням (зниженням) іншої змінної, тоді така функція – монотонна, в іншому випадку функція – немонотонна.
Статистичний зв`язок – це такий зв`язок, коли одному значенню певного показника відповідає декілька значень іншого. Така залежність існує, наприклад, між масою та довжиною тіла. Одному значенню довжини тіла може відповідати декілька значень маси тіла і навпаки.
Кореляційний зв`язок представляє собою деяке об`єднання вищезазна-чених видів зв`язку. В якості числової характеристики ймовірності зв`язку використовують коефіцієнти кореляції. Коефіцієнт кореляції – це якісна міра сили і напряму ймовірного зв`язку двох змінних і знаходиться в межах від -1 до +1.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|