
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Общая схема решения квадратного неравенства , где х - неизвестное; - действительные числа или функции от параметра, причем .
Решить неравенства а)  ; б)
; б) 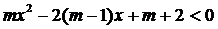 и обсудить в каждом случае схему решения.
и обсудить в каждом случае схему решения.
а)  .
.
Решение.
1) 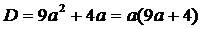 ;
;  , если
, если 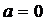 или
или 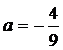 , тогда имеем: при
, тогда имеем: при 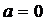 :
: 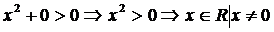 ;
;
при 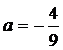 :
: 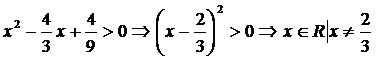 ;
;
2)
 |
Знаки
 в зависимости от параметра а:
в зависимости от параметра а:
Видим, что при 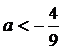 ,
, 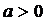
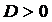 , тогда
, тогда  , где
, где 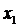 и
и 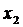 - корни квадратного трехчлена
- корни квадратного трехчлена 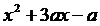 :
: 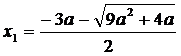 ,
, 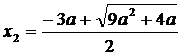 ;
;
при 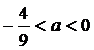
 , тогда х - любое из R.
, тогда х - любое из R.
Ответ: 1) при 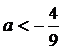 и при
и при 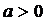
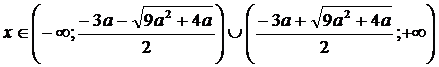 ;
;
2) при 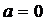 ,
, 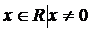 ;
; 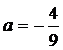 ,
, 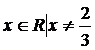 ;
;
3) при 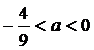 ,
, 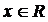 .
.
б) 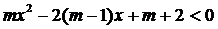
Решение.
1) 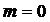 :
: 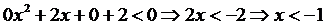 ;
;
2)  :
: 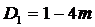 . Знаки
. Знаки  :
:
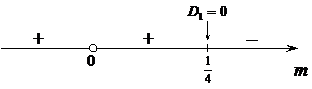 |
Если
 , то имеем
, то имеем
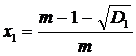 ,
, 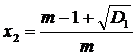 .
.
3) Используя график квадратичной функции (Приложение 1), имеем:
а) 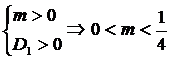 , тогда
, тогда 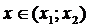 ;
;
б) 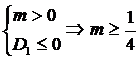 , тогда решений нет.
, тогда решений нет.
4) а)  , тогда
, тогда 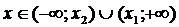 , учитывая, что при
, учитывая, что при 
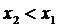 !
!
б) 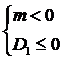 ни при каких значениях
ни при каких значениях 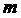 .
.
Ответ: 1)  имеем
имеем  ;
;
2) при 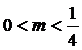 ,
, 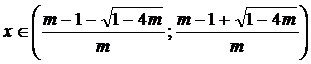 ;
;
3) при 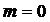 ,
, 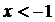 ; 4) при
; 4) при 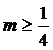 решений нет.
решений нет.
Общая схема решения квадратного неравенства , где х - неизвестное; - действительные числа или функции от параметра, причем .
1. Решить неравенство при .
2. Найти дискриминант и корни квадратного трехчлена, считая, что ; указать знаки дискриминанта в зависимости от параметра.
3. Решить неравенство, если:
а) 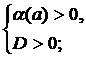 б)
б) 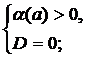 в)
в) 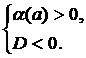
4. Решить неравенство, если:
а) 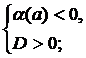 б)
б) 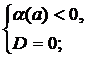 в)
в) 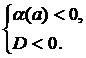
5. Записать ответ.
ПРИЛОЖЕНИЕ 1

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|