
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Четвертая часть. (№13 и №15 в ЕГЭ по математике профильного уровня). Уравнения и неравенства. Ответы с пояснением. Первая часть. Вторая часть. Третья часть. Четвертая часть. №15 вариант 11
Четвертая часть
(№13 и №15 в ЕГЭ по математике профильного уровня)
Уравнения и неравенства
№ 514623
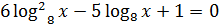
№15 вариант 11

№15 вариант 20
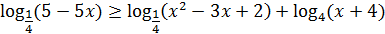
Ответы с пояснением
Первая часть
№ 26646
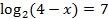
1) 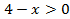
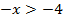
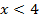
2) 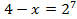
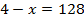
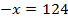
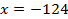
3) 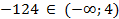
Ответ: -124
№ 26647 Ответ: 21
№ 26658 Ответ: -42
№ 26649
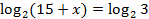
1) 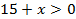
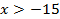
2) 
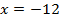
3) 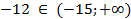
Ответ: -12
№ 26657 Ответ: 6
№ 77380 Ответ: 5
№ 77381 Ответ: 2
№ 77382

1) 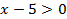 и
и 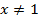

2) 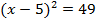
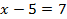
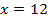
3) 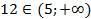 и
и 
Ответ: 12
№ 315120
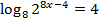
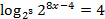
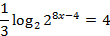
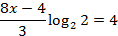
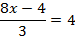

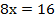
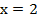
Ответ: 2
№ 315535 Ответ: 13, 4
Вторая часть
№ 26843
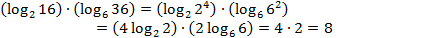
№ 26848
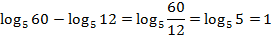
№ 26851
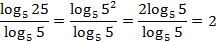
№ 26853

№ 510939
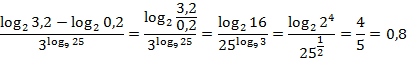
№ 77416
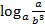 , если
, если 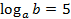
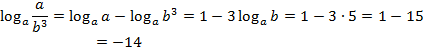
№ 77415
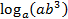 , если
, если 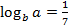
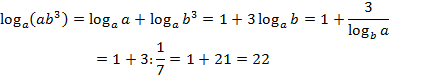
№ 77417
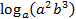 ,
, 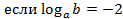
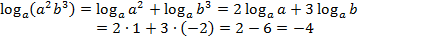
№ 98471
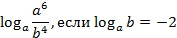
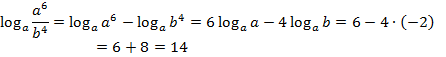
Третья часть
№ 27994
Задача сводится к решению неравенства 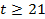 при заданных значениях начального напряжения на конденсаторе
при заданных значениях начального напряжения на конденсаторе 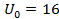 кВ, сопротивления резистора
кВ, сопротивления резистора 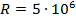 Ом и ёмкости конденсатора
Ом и ёмкости конденсатора  Ф:
Ф:
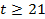
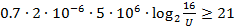
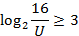
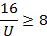
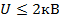
Ответ: 2
№ 27995
Задача сводится к решению уравнения 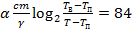 при заданных значениях теплоёмкости воды
при заданных значениях теплоёмкости воды 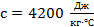 , коэффициента теплообмена
, коэффициента теплообмена 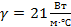 , постоянной
, постоянной 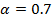 , температуры помещения
, температуры помещения 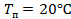 , и расхода воды
, и расхода воды 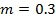 кг/с:
кг/с:

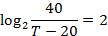

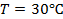
Ответ: 30
№ 27996
Задача сводится к решению уравнения 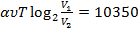 при заданных значениях постоянной
при заданных значениях постоянной 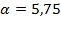 , температуры воздуха
, температуры воздуха 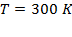 , количества вещества воздуха
, количества вещества воздуха 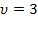 моль и объема воздуха
моль и объема воздуха  л:
л:
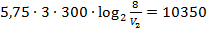
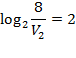

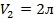
Ответ: 2
Четвертая часть
№ 514623
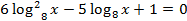
ОДЗ: 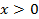
Пусть 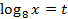
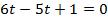
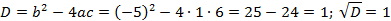
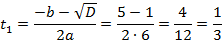
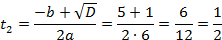
Если 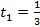 , то
, то 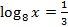
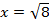
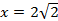
Если 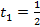 , то
, то 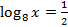
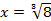
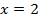
Ответ: 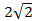 ;
; 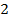
№15 вариант 11
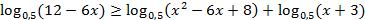
ОДЗ неравенства:
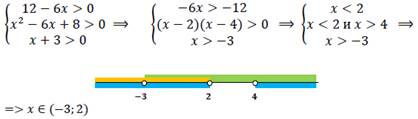
Преобразуем неравенство:
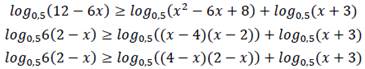
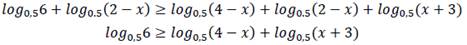
Сумма логарифмов равна логарифму произведения подлогарифмических выражений:
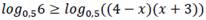
Так как основание логарифмического неравенства 0 < 0, 5 < 1, то логарифмическое неравенство равносильно неравенству:

Решим неравенство методом интервалов, найдем нули квадратного трехчлена:
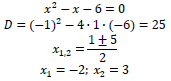
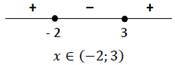
Учитывая ОДЗ неравенства, найдем его решение:
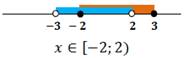
Ответ: [-2; 2)
№15 вариант 20

ОДЗ неравенства:
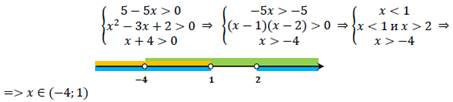
Преобразуем неравенство:
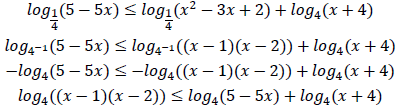
Сумма логарифмов равна логарифму произведения подлогарифмических выражений:
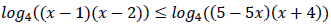
Так как основание логарифмического неравенства 4 > 1, то логарифмическое неравенство равносильно неравенству:
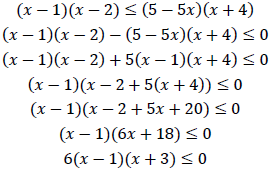
Решим неравенство методом интервалов, нули левой части неравенства:
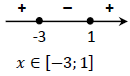
Учитывая ОДЗ неравенства, найдем его решение:

Ответ: 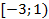
Математика
Сборник заданий
по теме «Логарифмы»
Автор: Савина София Сергеевна
Рецензент: Оганисян Ирина Михайловна
Задания взяты с сайта РешуЕГЭ и сборника И. В. Ященко
Дата создания: январь 2021
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|