Информационная карта. Тема урока: Рациональные неравенства. Основные приемы их решения.. 1. Изучение нового материала. Решение целых неравенств. Пример.

Стр 1 из 2Следующая ⇒

Урок

Задание: изучить материал урока, выполнить упражнения и домашнее задание.

Информационная карта

Тема урока: Рациональные неравенства. Основные приемы их решения.

Цель: научиться решать рациональные неравенства.

Ход урока:

1. Изучение нового материала

Рациональное неравенство – это неравенство с переменными, обе части которого есть рациональные выражения.

Неравенства подразделяются на целые и дробные.

Определение: Рациональное неравенство будем называть целым, если обе его части – целые рациональные выражения.

Определение: Дробно рациональное неравенство – это рациональное неравенство, хотя бы одна часть которого – дробное выражение.

Решение целых неравенств

Пример .

Найдите решение целого рационального неравенства x·(x+3)+2·x≤ (x+1)²+1.

Решение.

x·(x+3)+2·x− (x+1)²− 1≤ 0, раскроем скобки, приведём подобные, получим: 3·x− 2≤ 0, 3·x≤ 2, x≤ 2/3.

Ответ: x≤ 2/3.

Пример.

Выполните решение неравенства x+6+2·x³− 2·x·(x²+x− 5)> 0.

Решение.

Преобразуем целое выражение, находящееся в левой части, в многочлен:
x+6+2·x³− 2·x³− 2·x²+10·x> 0,
− 2·x²+11·x+6> 0.

Получили квадратное неравенство, которое равносильно исходному неравенству.

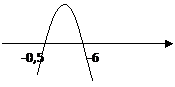Находим корни квадратного трехчлена − 2·x²+11·x+6:

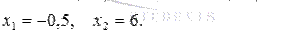
Делаем схематический чертеж, на котором отмечаем найденные нули, и учитываем, что ветви параболы направлены вниз, так как старший коэффициент отрицательный:

Так как мы решаем неравенство со знаком >, то нас интересуют промежутки, на которых парабола располагается выше оси абсцисс. Это имеет место на интервале (− 0, 5, 6), он и является искомым решением.

Ответ: (− 0, 5, 6).

12 Следующая ⇒