7.2 Критерий Михайлова

Критерий Михайлова дает возможность судить об устойчивости системы по годографу, описываемому концом характеристического вектора замкнутой системы, который может быть получен из уравнения (6. 3):

М(р) = D(p) + G(p). (6. 8)

Если заменить р на jω и изменять ω от 0 до ∞, то вектор своим концом опишет в комплексной плоскости кривую, называемую годографом Михайлова. Выражение (6. 8) представляет полином m-го порядка, который может быть разложен (при р = jω ) на множители по теореме Безу:

М(jω ) = (jω – p₁)( jω – p₂)…( jω – р_m), (6. 9)

где р₁, р₂, …, р_m – корни уравнения (6. 3).

Уравнение (6. 9) написано в предположении, что замкнутая система устойчива. Правая часть этого уравнения представляет произведение векторов, расположенных слева от мнимой оси в плоскости корней (рисунок 6. 3, а). Так как векторы (jω – p_k), соответствующие вещественным корням, совпадают с осью абсцисс, то при изменении ω от 0 до ∞ каждый из них повернется на угол π /2. Каждая же пара комплексно-сопряженных корней повернется при этом на угол π. Действительно, вектор (jω – р₂) при изменении ω от 0 до ∞ повернется на угол α ₁, а вектор (jω – р₃) на угол α ₂. Так как ∟ ABO = ∟ BAO = α ₂ (Δ OAB — равнобедренный), то результирующий угол поворота обоих векторов α ₁ + α ₂ = π.

Таким образом, вектор М(jω ), представляющий произведение m векторов, аргументы которых при умножении складываются, повернется при этих условиях на угол m(π /2).

При ω =0 годограф Михайлова отсекает на вещественной оси в положительном направлении отрезок, равный свободному члену характеристического уравнения. Начало характеристического вектора совпадает с началом координат. Поэтому, если система устойчива, характеристический вектор при своем вращении нигде не должен обращаться в нуль.

Критерий Михайлова формулируется следующим образом: замкнутая система устойчива в том случае, если вектор кривой Михайлова при изменении ω от 0 до ∞ проходит в положительном направлении m квадрантов комплексной плоскости, начиная свое движение от положительной вещественной полуоси, и при этом нигде не обращается в нуль (m – порядок характеристического уравнения замкнутой системы).

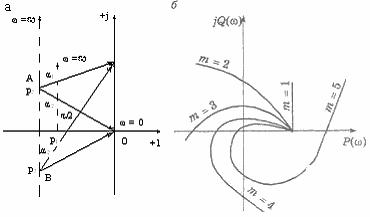
Рисунок. 6. 3 – Исследование устойчивости по Михайлову: а) график к доказательству критерия Михайлова; б) годограф Михайлова

На рисунке 6. 3, б приведены годографы Михайлова для устойчивых замкнутых систем, описываемых уравнениями различных порядков (m = 1, 2, 4, 5). Система будет неустойчивой в случае, если полином M(jω ), определяемый уравнением (7. 9), имеет корни с положительной вещественной частью. Число этих корней r можно определить по виду годографа. Если полный угол поворота вектора M( ω ) равен (m – 2r)(π /2), то число правых корней равно r.

Значение частот ω _i, при которых кривая Михайлова пересекает вещественные и мнимые полуоси комплексной плоскости, находят из уравнений:

Х(ω ) = 0 (6. 10)

У(ω ) = 0 (6. 11)

Вещественную Х(ω ) и мнимую У(ω ) части функции Михайлова М(ω ) можно представить графически (рисунок 6. 4).

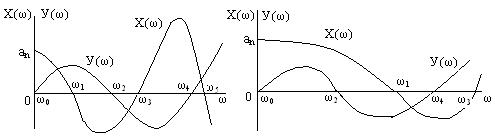
Рисунок 6. 4 – АФХ замкнутой САУ: а) устойчивая; б) неустойчивая

В соответствии с критерием Михайлова для устойчивой САУ будет обязательно выполняться условия (рисунок 6. 4, а):

ω ₀< ω ₁ < ω ₂ < ω ₃ <..... < ω _n (6. 12)

Если корни ω i уравнений (6. 10, 6. 11) будут немонотонно возрастать, то САУ будет нестойчивой (рисунок 6. 2, б).

Следствие критерия Михайлова: система будет устойчива, когда вещественная и мнимая части функции Михайлова приравненные к нулю, имеют все действительные и монотонно возрастающие корни, при чем общее число этих корней равно порядку характеристического уравнения n, и при ω = 0 Х(0)> 0 и У(0) = 0.

Для уравнений до шестого порядка включительно можно легко определить устойчивость, не вычерчивая кривую Михайлова, а определяя только чередование знаков Х(ω ) при подстановке корней с возрастанием ω i, найденных из уравнения (6. 11) У(ω ) = 0.

⇐ Предыдущая 12