
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
1. Введение алгоритма.. Находим абсциссу точки касания;. Находим f(a);. Находим f ‘(x); . Находим f ‘(a);. Подставили найденные выражения а; f(x) и f ‘(a) в формулу y=f(a)+f ‘ (a)(x-a).. 2. Усвоение алгоритма.
А10
Тема: “ Уравнение касательной к графику функции”.
Дата: 07. 04. 2020 г.
Цель:
1) Научиться составлять уравнение касательной к графику функции.
2) Научиться применять уравнение касательной в нестандартной ситуации.
Ход урока.
1. Введение алгоритма.
1) Сегодня на уроке мы продолжим изучать тему «уравнение касательной к графику функции».
2) Напишите в тетради уравнение касательной y=f(a)+f ‘(a)(x-a).
Задание:
Составьте уравнение касательной к графику функции y=tg x в точке х=а.
Решение:
1) х=a;
2) f (a)=tg a;
3) f ‘(x)= 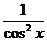 ;
;
4) f ‘(a)= 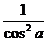 ;
;
5) y=tg a( 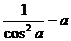 ).
).
Чтобы быстро и верно составить уравнение касательной мы выполняем шаги.
1) Что мы делаем в начале?
Находим абсциссу точки касания;
2) Что делаем потом?
Находим f(a);
3) Что делаем дальше?
Находим f ‘(x);
4) Затем?
Находим f ‘(a);
5) И как составляли уравнение?
Подставили найденные выражения а; f(x) и f ‘(a) в формулу y=f(a)+f ‘ (a)(x-a).
Составьте самостоятельно алгоритм составления уравнения касательной к графику функции y=f(x).
Алгоритм составления касательной к графику функции:
1) Найти абсциссу f(x) точки касания: a.
2) Вычислить f(a);
3) Найти f ‘(x);
4) Вычислить f’(a);
5) Подставить найденные числа a; f(a) и f ‘(a) в формулу y=f(a)=f ‘(a)(x-a)
2. Усвоение алгоритма.
| Примеры | Шаг 1 a | Шаг 2 f(a) | Шаг 3 f ‘(x) | Шаг 4 f ‘(a) | Уравнение касательной |
f (x)=x 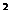 ; a=3 ; a=3
| |||||
f (x)=x 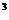 ; a=1 ; a=1
| |||||
f (x)=2-x-x 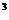 ; a=0 ; a=0
| |||||
f (x)=x 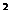 -3x+5;
a=1 -3x+5;
a=1
| |||||
f (x)=sin2x; a= 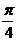
| |||||
f (x)= 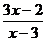 ; a=2 ; a=2
| |||||
f (x)=cos 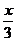 ; a=0 ; a=0
|
1) Самостоятельно заполнить таблицу (сфотографировать и выслать в сообщения)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|