Примеры.. Решение.. Решение.. Решение.. Решение.. Парабола.

Примеры.

2. 265. Построить гиперболу 16x2− 9y2=144. 16x2− 9y2=144. Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.

Решение.

Приведем уравнение гиперболы к каноническому виду:

16x2− 9y2=144|: 144⇒ 16x2144− 9y2144=1⇒ 16x2− 9y2=144|: 144⇒ 16x2144− 9y2144=1⇒

⇒ x29− y216=1⇒ x232+y242=1. ⇒ x29− y216=1⇒ x232+y242=1.

а) Находим полуоси a=3, a=3, b=4. b=4.

б) Фокусы найдем по формулам F1(− c, 0)F1(− c, 0) и F2(c, 0), F2(c, 0), где c=a2+b2− − − − − − √: c=a2+b2:

c=32+42− − − − − − √ =25− − √ =5⇒ F1(− 5, 0), F2(5, 0). c=32+42=25=5⇒ F1(− 5, 0), F2(5, 0).

в) Эксцентриситет e=ca=53. e=ca=53.

г) Асимптоты гиперболы находим по формулам y=±bax: y=±bax:

y=±43x. y=±43x.

д) Уравнения директрис находим по формулам D1: x=− a/eD1: x=− a/e и D2: x=a/e: D2: x=a/e:

D1: x=− 35/3=− 95D1: x=− 35/3=− 95 и D2: x=35/3=95. D2: x=35/3=95.

Сделаем рисунок:

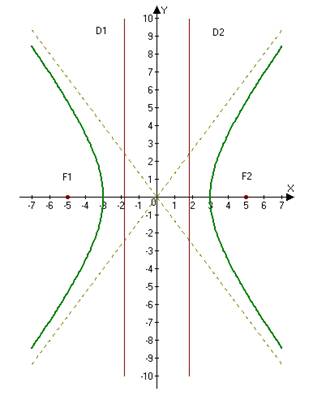
Ответ: а) a=3, a=3, b=4; b=4; б) F1(− 5, 0), F2(5, 0); F1(− 5, 0), F2(5, 0); в) e=53; e=53; г) y=±43x; y=±43x; д ) D1: x=− 95D1: x=− 95 и D2: x=95. D2: x=95.

2. 269 (a). Установить, что уравнение 16x2− 9y2− 64x− 54y− 161=016x2− 9y2− 64x− 54y− 161=0 определяет гиперболу, найти ее центр C, C, полуоси, эксцентриситет, уравнения асимптот и директрис.

Решение.

Приведем заданное уравнение к каноническому виду, для этого выделим полные квадраты:

16x2− 9y2− 64x− 54y− 161=(16x2− 64x)− (9y2+54y)− 161=16x2− 9y2− 64x− 54y− 161=(16x2− 64x)− (9y2+54y)− 161=

16(x2− 4x+4− 4)− 9(y2+6y+9− 9)− 161=16(x− 2)2− 64− 9(y+3)2+81− 161=16(x2− 4x+4− 4)− 9(y2+6y+9− 9)− 161=16(x− 2)2− 64− 9(y+3)2+81− 161=

16(x− 2)2− 9(y+3)2− 144=0⇒ 16(x− 2)2− 9(y+3)2=144|: 144⇒ 16(x− 2)2− 9(y+3)2− 144=0⇒ 16(x− 2)2− 9(y+3)2=144|: 144⇒

(x− 2)29− (y+3)216=1⇒ (x− 2)29− (y+3)216=1. (x− 2)29− (y+3)216=1⇒ (x− 2)29− (y+3)216=1.

Это уравнение гиперболы. Центр имеет координаты C=(x0, y0)=(2, − 3); C=(x0, y0)=(2, − 3); полуоси a=3, a=3, b=4. b=4.

c=a2+b2− − − − − − √ ⇒ c=9+16− − − − − √ =25− − √ =5⇒ e=ca=53. c=a2+b2⇒ c=9+16=25=5⇒ e=ca=53.

Асимптоты гиперболы c центром в начале координат, находим по формулам y=±bax, y=±bax, а с центром в точке C=(x0, y0)− C=(x0, y0)− по формуле y− y0=±ba(x− x0), y− y0=±ba(x− x0),

y+3=43(x− 2)⇒ 3y+9=4x− 8⇒ 4x− 3y− 17=0. y+3=43(x− 2)⇒ 3y+9=4x− 8⇒ 4x− 3y− 17=0.

y+3=− 43(x− 2)⇒ 3y+9=− 4x+8⇒ 4x+3y+1=0. y+3=− 43(x− 2)⇒ 3y+9=− 4x+8⇒ 4x+3y+1=0.

Уравнения директрис для эллипса с центром в начале координат находим по формулам D1: x=− a/eD1: x=− a/e и D2: x=a/e: D2: x=a/e:

D1: x=− 35/3=− 95D1: x=− 35/3=− 95 и D2: x=35/3=95. D2: x=35/3=95. Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения D1: x=x0− a/eD1: x=x0− a/e и D2: x=x0+a/e: D2: x=x0+a/e:

D1: x=2− 95=10− 95=15⇒ 5x− 1=0D1: x=2− 95=10− 95=15⇒ 5x− 1=0

D2: x=2+95=10+95=195⇒ 5x− 19=0D2: x=2+95=10+95=195⇒ 5x− 19=0

Ответ: C=(2, − 3); C=(2, − 3); a=3, a=3, b=4; b=4; e=53, e=53, 4x− 3y− 17=0, 4x− 3y− 17=0, 4x+3y+1=0, 4x+3y+1=0, D1: 5x− 1=0, D1: 5x− 1=0, D2: 5x− 19=0. D2: 5x− 19=0.

2. 272. Убедившись, что точка M(− 5, 9/4)M(− 5, 9/4) лежит на гиперболе x216− y29=1, x216− y29=1, найти фокальные радиусы этой точки и расстояния этой точки до директрис.

Решение.

Проверим, что заданная точка лежит на гиперболе:

x216− y29=1⇒ (− 5)216− (9/4)29=2516− 8116⋅ 9=25⋅ 9− 81144=144144=1. x216− y29=1⇒ (− 5)216− (9/4)29=2516− 8116⋅ 9=25⋅ 9− 81144=144144=1.

Следовательно, точка M(− 5, 9/4)M(− 5, 9/4) лежит на гиперболе x216− y29=1. x216− y29=1.

Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы:

c=a2+b2− − − − − − √ ⇒ c=16+9− − − − − √ =25− − √ =5c=a2+b2⇒ c=16+9=25=5 Следовательно, фокусы имеют координаты F1(− 5, 0), F2(5, 0). F1(− 5, 0), F2(5, 0).

Фокальные радиусы точки, можно найти по формулам r1=|F1M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ |r1=|F1M¯ | и r2=|F2M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ |. r2=|F2M¯ |.

F1M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ =(− 5− (− 5), 9/4)=(0, 9/4)⇒ |F1M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ =(9/4)2− − − − − √ |=9/4. F1M¯ =(− 5− (− 5), 9/4)=(0, 9/4)⇒ |F1M¯ =(9/4)2|=9/4.

F2M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ =(− 5− 5, 9/4)=(− 10, 9/4)⇒ |F1M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ =102+(9/4)2− − − − − − − − − − √ |=F2M¯ =(− 5− 5, 9/4)=(− 10, 9/4)⇒ |F1M¯ =102+(9/4)2|=

=100+81/16− − − − − − − − − − √ =168116− − − − − √ =414. =100+81/16=168116=414.

Чтобы найти расстояния от точки MM до директрис, найдем уравнения директрис по формулам D1: x=− a/eD1: x=− a/e и D2: x=a/e: D2: x=a/e:

e=ca=54; e=ca=54;

D1: x=− 45/4⇒ x=− 165⇒ 5x+16=0; D1: x=− 45/4⇒ x=− 165⇒ 5x+16=0;

D2: x=45/4⇒ x=165⇒ 5x− 16=0; D2: x=45/4⇒ x=165⇒ 5x− 16=0;

Расстояние от точки P(x0, y0)P(x0, y0) до прямой L: Ax+By+C=0L: Ax+By+C=0 вычисляется по формуле

d=∣ ∣ ∣ Ax0+By0+CA2+B2− − − − − − − √ ∣ ∣ ∣. d=|Ax0+By0+CA2+B2|.

Таким образом, расстояние от точки M(5, 9/4)M(5, 9/4) до прямой D1: 5–√ x+16=0D1: 5x+16=0

d1=∣ ∣ ∣ 5⋅ 5+1652− − √ ∣ ∣ ∣ =415; d1=|5⋅ 5+1652|=415;

расстояние от точки M(5, 9/4)M(5, 9/4) до прямой D2: 5–√ x− 16=0D2: 5x− 16=0

d2=∣ ∣ ∣ 5⋅ 5− 1652− − √ ∣ ∣ ∣ =95. d2=|5⋅ 5− 1652|=95.

Ответ: r1=9/4, r1=9/4, r2=414; r2=414; d1=415; d1=415; d2=95. d2=95.

2. 273. Найти точки гиперболы x29− y216=1, x29− y216=1, находящиеся на расстоянии 77 от фокуса F1. F1.

Решение.

Из уравнения гиперболы находим полуоси: a=3, b=4. a=3, b=4. Следовательно, c=a2+b2− − − − − − √ ⇒ c=9+16− − − − − √ =25− − √ =5. c=a2+b2⇒ c=9+16=25=5.

Отсюда находим F1=(− 5, 0). F1=(− 5, 0).

Геометрическое место точек, расположенных на расстоянии 77 от фокуса F1, F1, это окружность с центром в точке F1=(− 5, 0)F1=(− 5, 0) и радиусом r=7: r=7:

(x+5)2+y2=72. (x+5)2+y2=72.

Чтобы найти точки гиперболы x29− y216=1, x29− y216=1, находящиеся на расстоянии 77 от фокуса F1, F1, решим систему уравнений

{x29− y216=1(x+5)2+y2=72{x29− y216=1(x+5)2+y2=72

⇒ {x29− y216=1y2=72− (x+5)2⇒ {x29− 72− (x+5)216=1y2=72− (x+5)2⇒ {x29− y216=1y2=72− (x+5)2⇒ {x29− 72− (x+5)216=1y2=72− (x+5)2

⇒ {16x2− 9(49− x2− 10x− 25)=144y2=72− (x+5)2⇒ ⇒ {16x2− 9(49− x2− 10x− 25)=144y2=72− (x+5)2⇒

⇒ {16x2− 216+9x2+90x=144y2=72− (x+5)2⇒ ⇒ {16x2− 216+9x2+90x=144y2=72− (x+5)2⇒

⇒ {25x2+90x− 360=0y2=72− (x+5)2⇒ {5x2+18x− 72=0y2=72− (x+5)2⇒ {25x2+90x− 360=0y2=72− (x+5)2⇒ {5x2+18x− 72=0y2=72− (x+5)2

Решим уравнение 5x2+18x− 72=0: 5x2+18x− 72=0:

D=182+4⋅ 5⋅ 72=324+1440=1764=422. D=182+4⋅ 5⋅ 72=324+1440=1764=422.

x1=− 18+4210=2410=2, 4; x1=− 18+4210=2410=2, 4; x2=− 18− 4210=− 6. x2=− 18− 4210=− 6.

Находим соответствующие координаты y: y: y1=±24− 2, 42− 10⋅ 2, 4− − − − − − − − − − − − − − − √ =− 5, 76− − − − − √ y1=±24− 2, 42− 10⋅ 2, 4=− 5, 76 - нет корней.

y2=±24− 62+10⋅ 5− − − − − − − − − − − − √ =±43–√. y2=±24− 62+10⋅ 5=±43.

Ответ: (− 6, ±43–√ ). (− 6, ±43).

Парабола.

Парабола с каноническим уравнением y2=2px, p> 0, y2=2px, p> 0, имеет форму изображенную на рисунке.

Число pp называется параметром параболы. Точка O− O− ее вершиной, а ось OxOx - осью параболы.

Точка F(p2, 0)F(p2, 0) называется фокусом параболы, вектор FM¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ − FM¯ − фокальным радиус-векторам, а число r=|FM¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ |− r=|FM¯ |− фокальным радиусом точки M, M, принадлежащей параболе.

Прямая D: x=− p/2D: x=− p/2 перпендикулярная оси и проходящая на расстоянии p/2p/2 от вершины параболы, называется ее директрисой.

Примеры.

2. 285 (а). Построить параболу y2=6xy2=6x и найти ее параметры.

Решение.

Параметр pp параболы можно найти из канонического уравнения y2=2px: y2=2px:

y2=6x⇒ y2=2⋅ 3x⇒ p=2. y2=6x⇒ y2=2⋅ 3x⇒ p=2.

Сделаем рисунок:

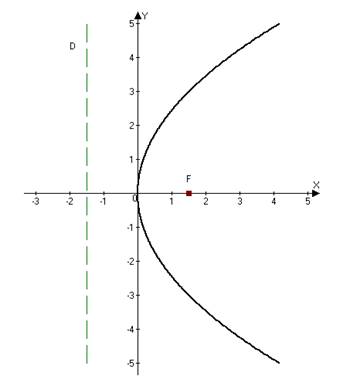
Ответ: p=3. p=3.

{jumi[*4]}

2. 286 (а). Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси OxOx и p=1/2. p=1/2.

Решение.

Поскольку парабола расположена в левой полуплоскости, симметрично относительно оси Ox, Ox, то уравнение параболы будет иметь вид y2=− 2px. y2=− 2px. Подставляя заданное значение параметра, находим уравнение параболы:

y2=− 2⋅ 12x=− x. y2=− 2⋅ 12x=− x.

Ответ: y2=− x. y2=− x.

2. 288 (а). Установить, что уравнение y2=4x− 8y2=4x− 8 определяет параболу, найти координаты ее вершины AA и величину параметра p. p.

Решение.

Уравнение параболы, центр которой сдвинут в точку (x0, y0), (x0, y0), имеет вид (y− y0)2=2p(x− x0)2. (y− y0)2=2p(x− x0)2.

Приведем заданное уравнние к такому виду:

y2=4(x− 2). y2=4(x− 2).

Таким образом, y2=4(x2− 2)y2=4(x2− 2) - парабола с центром в точке (0, 2). (0, 2). Параметр p=2. p=2.

Ответ: C(0, 2), C(0, 2), p=2. p=2.

2. 290. Вычислить фокальный параметр точки MM параболы y2=12x, y2=12x, если y(M)=6. y(M)=6.

Решение.

Чтобы найти фокальный параметр точки M, M, найдем ее координаты. Для этого подставим в уравнение параболы координату y: y:

62=12x⇒ 36=12x⇒ x=3. 62=12x⇒ 36=12x⇒ x=3.

Таким образом, точка MM имеет координаты (3, 6). (3, 6).

Из уравнения параболы y2=12xy2=12x находим параметр параболы: y2=2⋅ 6x⇒ p=6. y2=2⋅ 6x⇒ p=6. Следовательно фокус параболы имеет координаты F(3, 0). F(3, 0).

Далее находим фокальный параметр точки:

r=|FM|=(3− 3)2+(6− 0)2− − − − − − − − − − − − − − − √ =6. r=|FM|=(3− 3)2+(6− 0)2=6.

Ответ: 6. 6.

2. 298. Из фокуса параболы y2=12xy2=12x под острым углом α α к оси OxOx направлен луч света, причем tgα =34. tgα =34. Написать уравнение прямой, на которой лежит луч, отраженный от параболы.

Решение.

Найдем координаты фокуса. Из канонического уравнения параболы y2=2pxy2=2px находим параметр: y2=12x=2⋅ 6x⇒ p=6. y2=12x=2⋅ 6x⇒ p=6.

Координаты фокуса F(p/2, 0)⇒ F(3, 0). F(p/2, 0)⇒ F(3, 0).

Далее находим уравнение прямой, которая проходит через точку (3, 0)(3, 0) под углом α: tgα =34α: tgα =34 к оси OX. OX. Уравнение ищем в виде y=kx+b, y=kx+b, где k=tgα =34. k=tgα =34.

y=34x+by=34x+b

Чтобы найти b, b, в уравнение прямой подставим координаты точки (3, 0): (3, 0):

0=34⋅ 3+b⇒ b=− 94. 0=34⋅ 3+b⇒ b=− 94. Таким образом, уравнение луча, направленного из фокуса y=34x− 94. y=34x− 94.

Далее, найдем точку пересечения найденной прямой с параболой:

{y=34x− 94y²=12x⇒ {3x− 4y− 9=0x=y²12⇒ ⎧ ⎩ ⎨ 3y212− 4y− 9=0x=y212⇒ {y=34x− 94y2=12x⇒ {3x− 4y− 9=0x=y212⇒ {3y212− 4y− 9=0x=y212⇒

{y2− 16y− 36=0x=y212{y2− 16y− 36=0x=y212

y2− 16y− 36=0y2− 16y− 36=0

D=256+4⋅ 1⋅ 36=256+144=400. D=256+4⋅ 1⋅ 36=256+144=400.

y1=16+202=18y2=16− 202=− 2. y1=16+202=18y2=16− 202=− 2.

Поскольку по условию луч падает под острым углом, то мы рассматриваем только положительную координату y=18. y=18. Соответствующее значение x=18212=32412=27. x=18212=32412=27.

Таким образом, луч пересекает параболу в точке (27, 18). (27, 18).

Далее найдем уравнение касательной к параболе в найденной точке (27, 18)(27, 18) по формуле (y− y0)=y′ (x0)(x− x0): (y− y0)=y′ (x0)(x− x0):

y=12x− − − √ ⇒ y′ =12− − √ 12x− − √ =3–√ x− − √ ⇒ y=12x⇒ y′ =1212x=3x⇒

⇒ y′ (27)=3–√ 27− − √ =13. ⇒ y′ (27)=327=13.

y(27)=18. y(27)=18.

Подставляем все найденные значения в уравнение касательной:

y− 18=13(x− 27)⇒ 3y− 54=x− 27⇒ x− 3y+27=0. y− 18=13(x− 27)⇒ 3y− 54=x− 27⇒ x− 3y+27=0.

Далее, найдем угол β β между лучем y=34x− 94y=34x− 94 и касательной x− 3y+27=0. x− 3y+27=0. Для этого оба уравнения запишем в виде y=k1x+b1y=k1x+b1 и y=k2+b2y=k2+b2 угол вычислим по формуле tg(L1, L2)=k1− k21+k1⋅ k2tg(L1, L2)=k1− k21+k1⋅ k2

L1: y=34x− 94⇒ k1=34; L1: y=34x− 94⇒ k1=34;

L2: x− 3y+27=0⇒ y=13x+9⇒ k2=13. L2: x− 3y+27=0⇒ y=13x+9⇒ k2=13.

tgβ =tg(L1, L2)=34− 131+3413=51254=13. tgβ =tg(L1, L2)=34− 131+3413=51254=13.

Легко увидеть, что угол между лучем L1, L1, направленным из фокуса и его отражением равен π − 2β, π − 2β, а угол между отраженным лучем и осью OxOx π − (π − 2β )− α =2β − α. π − (π − 2β )− α =2β − α.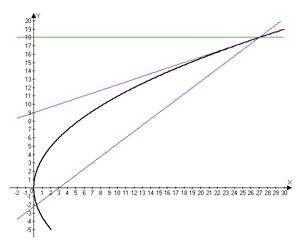

Зная tgβ =13tgβ =13 и tgα =k1=34tgα =k1=34 и вспоминая формулы для двойного угла тангенса и тангенс разности, находим tg(2β − α ): tg(2β − α ):

tg2β =2tgβ 1− tg2β =231− 19=2389=34. tg2β =2tgβ 1− tg2β =231− 19=2389=34.

tg(2β − α )=tg2β − tgα 1+tg2β tgα =34− 341+3434=0. tg(2β − α )=tg2β − tgα 1+tg2β tgα =34− 341+3434=0.

Следовательно, прямая, содержащая отраженный луч параллельна оси Ox. Ox. Так как она проходит через точку (27, 18), (27, 18), то можно записать ее уравнение y=18. y=18.

Ответ: y=18. y=18.

⇐ Предыдущая 123 Следующая ⇒