Эллипс.. Примеры.. Решение.. Решение.. Решение.. Гипербола.

Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

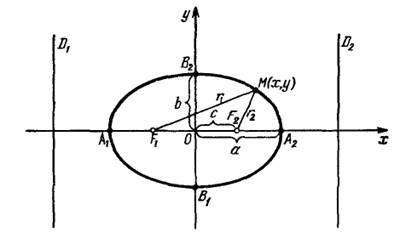
Эллипс.

Эллипс с каноническим уравнением x2a2+y2b2=1, a≥ b> 0, x2a2+y2b2=1, a≥ b> 0, имеет форму изображенную на рисунке.

Параметры aa и bb называются полуосями эллипса (большой и малой соответственно). Точки A1(− a, 0), A1(− a, 0), A2(a, 0), A2(a, 0), B1(0, − b), B1(0, − b), и B2(0, b), B2(0, b), еговершинами. Оси симметрии OxOx и OyOy - главными осями а центр симметрии O− O− центром эллипса.

Точки F1(− c, 0)F1(− c, 0) и F2(c, 0), F2(c, 0), где c=a2− b2− − − − − − √ ≥ 0, c=a2− b2≥ 0, называются фокусами эллипса векторы F1M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ F1M¯ и F2M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ − F2M¯ − фокальными радиус-векторами, а числа r1=|F1M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ |r1=|F1M¯ | и r2=|F2M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ |− r2=|F2M¯ |− фокальными радиусами точки M, M, принадлежащей эллипсу. В частном случае a=ba=b фокусы F1F1 и F2F2 совпадают с центром, а каноническое уравнение имеет вид x2a2+y2a2=1, x2a2+y2a2=1, или x2+y2=a2, x2+y2=a2, т. е. описывает окружность радиуса aa с центром в начале координат.

Число e=ca=1− b2a2− − − − − √ (0≤ e< 1)e=ca=1− b2a2(0≤ e< 1) называется эксцентриситетом эллипса и является мерой его " сплюснутости" (при e=0e=0 эллипс является окружностью. )

Прямые D1: x=− a/eD1: x=− a/e и D2: x=a/e, D2: x=a/e, перпендикулярные главной оси и проходящей на расстоянии a/ea/e от центра, называются директрисами эллипса.

Теорема. (Директориальное свойство эллипса)

Эллипс является множеством точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно e. e.

Примеры.

2. 246. Построить эллипс 9x2+25y2=225. 9x2+25y2=225. Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.

Решение.

Приведем уравнение эллипса к каноническому виду:

9x2+25y2=225|: 225⇒ 9x2225+25y2225=1⇒ 9x2+25y2=225|: 225⇒ 9x2225+25y2225=1⇒

⇒ x225+y29=1⇒ x252+y232=1. ⇒ x225+y29=1⇒ x252+y232=1.

а) Находим полуоси a=5, a=5, b=3. b=3.

б) Фокусы найдем по формулам F1(− c, 0)F1(− c, 0) и F2(c, 0), F2(c, 0), где c=a2− b2− − − − − − √: c=a2− b2:

c=52− 32− − − − − − √ =16− − √ =4⇒ F1(− 4, 0), F2(4, 0). c=52− 32=16=4⇒ F1(− 4, 0), F2(4, 0).

в) Эксцентриситет e=ca=45. e=ca=45.

г) Уравнения директрис находим по формулам D1: x=− a/eD1: x=− a/e и D2: x=a/e: D2: x=a/e:

D1: x=− 54/5=− 254D1: x=− 54/5=− 254 и D2: x=54/5=254. D2: x=54/5=254.

Сделаем рисунок:

Ответ: а) a=5, a=5, b=3; b=3; б) F1(− 4, 0), F2(4, 0); F1(− 4, 0), F2(4, 0); в) e=45; e=45; г) D1: x=− 254D1: x=− 254 и D2: x=254. D2: x=254.

{jumi[*3]}

2. 249 (a). Установить, что уравнение 5x2+9y2− 30x+18y+9=05x2+9y2− 30x+18y+9=0 определяет эллипс, найти его центр C, C, полуоси, эксцентриситет и уравнения директрис.

Решение.

Приведем уравнение эллипса к каноническому виду, для этого выделим полные квадраты:

5x2+9y2− 30x+18y+9=(5x2− 30x)+(9y2+18y)+9=5x2+9y2− 30x+18y+9=(5x2− 30x)+(9y2+18y)+9=

5(x2+6x+9− 9)+9(y2+2y+1− 1)+9=5(x+3)2− 45+9(y+1)2− 9+9=5(x2+6x+9− 9)+9(y2+2y+1− 1)+9=5(x+3)2− 45+9(y+1)2− 9+9=

5(x+3)2+9(y+1)2− 45=0⇒ 5(x+3)2+9(y+1)2=45|: 45⇒ 5(x+3)2+9(y+1)2− 45=0⇒ 5(x+3)2+9(y+1)2=45|: 45⇒

(x+3)29+(y+1)25=1⇒ (x+3)232+(y+1)2(5–√ )2=1. (x+3)29+(y+1)25=1⇒ (x+3)232+(y+1)2(5)2=1.

Это уравнение эллипса. Центр имеет координаты C=(x0, y0)=(− 3, − 1); C=(x0, y0)=(− 3, − 1); полуоси a=3, a=3, b=5–√. b=5.

c=a2− b2− − − − − − √ ⇒ c=9− 5− − − − √ =4–√ =2⇒ e=ca=23. c=a2− b2⇒ c=9− 5=4=2⇒ e=ca=23.

Уравнения директрис для эллипса с центром в начале координат находим по формулам D1: x=− a/eD1: x=− a/e и D2: x=a/e: D2: x=a/e:

D1: x=− 32/3=− 92D1: x=− 32/3=− 92 и D2: x=32/3=92. D2: x=32/3=92. Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения D1: x=x0− a/eD1: x=x0− a/e и D2: x=x0+a/e: D2: x=x0+a/e:

D1: x=3− 92=6− 92=− 32⇒ 2x+3=0D1: x=3− 92=6− 92=− 32⇒ 2x+3=0

D2: x=3+92=6+92=152⇒ 2x− 15=0. D2: x=3+92=6+92=152⇒ 2x− 15=0.

Ответ: C=(x0, y0)=(− 3, − 1); C=(x0, y0)=(− 3, − 1); a=3, a=3, b=5–√; b=5; e=23. e=23. D1: 2x+3=0, D1: 2x+3=0, D2: 2x− 15=0. D2: 2x− 15=0.

2. 252. Эллипс, главные оси которого совпадают с координатными осми, проходят через точки M1(2, 3–√ )M1(2, 3) и M2(0, 2). M2(0, 2). Написать его уравнение, найти фокальные радиусы точки M1M1 и расстояния этой точки до директрис.

Решение.

Поскольку оси эллипса совпадают с координатными осями, то центр эллипса совпадает с началом координат. Следовательно, из того, что точка (0, 2)(0, 2) принадлежит эллипсу, можно сделать вывод, что b=2. b=2.

Далее, чтобы найти a, a, подставим найденное значение bb и координаты точки M1(2, 3–√ )M1(2, 3) в каноническое уравнение эллипса x2a2+y2b2=1: x2a2+y2b2=1:

22a2+(3–√ )222=1⇒ 4a2+34=1⇒ 4a2=14⇒ a2=16⇒ a=4. 22a2+(3)222=1⇒ 4a2+34=1⇒ 4a2=14⇒ a2=16⇒ a=4.

Таким образом, уравнение эллипса x216+y24=1. x216+y24=1.

Далее найдем координаты фокусов:

c=a2− b2− − − − − − √ =16− 4− − − − − √ =23–√ ⇒ F1(− 23–√, 0), F2(23–√, 0). c=a2− b2=16− 4=23⇒ F1(− 23, 0), F2(23, 0).

Отсюда находим F1M1¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ =(2+23–√, 3–√ ), F1M1¯ =(2+23, 3), F2M1¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ =(2− 23–√, 3–√ ). F2M1¯ =(2− 23, 3).

Соответственно, r1=|F1M1¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ |=(2+23–√ )2+(3–√ )2− − − − − − − − − − − − − − − − √ =4+83–√ +12+3− − − − − − − − − − − − − − √ =r1=|F1M1¯ |=(2+23)2+(3)2=4+83+12+3= =16+83–√ +3− − − − − − − − − − − √ =(4+3–√ )2− − − − − − − − √ =4+3–√, =16+83+3=(4+3)2=4+3,

r2=|F2M1¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ |=(2− 23–√ )2+(3–√ )2− − − − − − − − − − − − − − − − √ =4− 83–√ +12+3− − − − − − − − − − − − − − √ =r2=|F2M1¯ |=(2− 23)2+(3)2=4− 83+12+3= =16− 83–√ +3− − − − − − − − − − − √ =(4− 3–√ )2− − − − − − − − √ =4− 3–√. =16− 83+3=(4− 3)2=4− 3.

Чтобы найти расстояния от точки M1M1 до директрис, найдем уравнения директрис по формулам D1: x=− a/eD1: x=− a/e и D2: x=a/e: D2: x=a/e:

e=ca=23√ 4=3√ 2; e=ca=234=32;

D1: x=− 43√ 2=− 83√ ⇒ 3–√ x+8=0; D1: x=− 432=− 83⇒ 3x+8=0;

D2: x=43√ 2=83√ ⇒ 3–√ x− 8=0. D2: x=432=83⇒ 3x− 8=0.

Расстояние от точки P(x0, y0)P(x0, y0) до прямой L: Ax+By+C=0L: Ax+By+C=0 вычисляется по формуле

d=∣ ∣ ∣ Ax0+By0+CA2+B2− − − − − − − √ ∣ ∣ ∣. d=|Ax0+By0+CA2+B2|.

Таким образом, расстояние от точки M1(2, 3–√ )M1(2, 3) до прямой D1: 3–√ x+8=0D1: 3x+8=0

d1=∣ ∣ ∣ ∣ ∣ 23–√ +8(3–√ )2− − − − − √ ∣ ∣ ∣ ∣ ∣ =23–√ +83–√; d1=|23+8(3)2|=23+83;

расстояние от точки M1(2, 3–√ )M1(2, 3) до прямой D2: 3–√ x− 8=0D2: 3x− 8=0

d2=∣ ∣ ∣ ∣ ∣ 23–√ − 8(3–√ )2− − − − − √ ∣ ∣ ∣ ∣ ∣ =8− 23–√ 3–√. d2=|23− 8(3)2|=8− 233.

Ответ: x216+y24=1, x216+y24=1, r1=4+3–√, r1=4+3, r2=4− 3–√, r2=4− 3, d1=8+23√ 3√, d1=8+233, d2=8− 23√ 3√. d2=8− 233.

Гипербола.

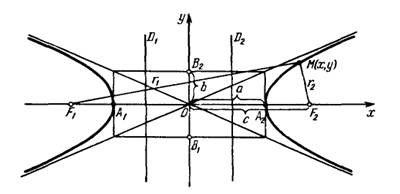
Гипербола с каноническим уравнением x2a2− y2b2=1, a, b> 0, x2a2− y2b2=1, a, b> 0, имеет форму изображенную на рисунке.

Параметры aa и bb называются полуосями гиперболы. Точки A1(− a, 0), A1(− a, 0), A2(a, 0)− A2(a, 0)− еевершинами. Оси симметрии OxOx и OyOy - действительной и мнимой осями а центр симметрии O− O− центром гиперболы.

Прямые y=±baxy=±bax являются асимптотами гиперболы.

Точки F1(− c, 0)F1(− c, 0) и F2(c, 0), F2(c, 0), где c=a2+b2− − − − − − √ ≥ 0, c=a2+b2≥ 0, называются фокусами гиперболы, векторы F1M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ F1M¯ и F2M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ − F2M¯ − фокальными радиус-векторами, а числа r1=|F1M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ |r1=|F1M¯ | и r2=|F2M¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ |− r2=|F2M¯ |− фокальными радиусами точки M, M, принадлежащей гиперболе.

Число e=ca=1+b2a2− − − − − √ (1< e< +∞ )e=ca=1+b2a2(1< e< +∞ ) называется эксцентриситетом гиперболы и является мерой ее " сплюснутости". В частном случае a=ba=b гипербола называется равносторонней; ее эксцентриситет равен e=2–√, e=2, а угол между асимптотами равен π /2. π /2.

Прямые D1: x=− a/eD1: x=− a/e и D2: x=a/e, D2: x=a/e, перпендикулярные главной оси и проходящей на расстоянии a/ea/e от центра, называются директрисами гиперболы.

Теорема. (Директориальное свойство гиперболы).

Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно e. e.

12 3 Следующая ⇒