Пример 3. Вычислить приближенно , заменяя приращение функции ее дифференциалом.

Пример 3. Вычислить приближенно , заменяя приращение функции ее дифференциалом.

Решение. Рассмотрим функцию 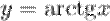. Необходимо вычислить ее значение в точке 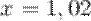. Представим данное значение в виде следующей суммы:

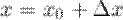
Величины и выбираются так, чтобы в точке можно было бы достаточно легко вычислить значение функции и ее производной, а было бы достаточно малой величиной. С учетом этого, делаем вывод, что , то есть , .

Вычислим значение функции 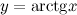в точке :

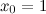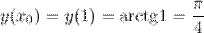
Далее продифференцируем рассматриваемую функцию и найдем значение :

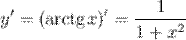
Тогда

Итак,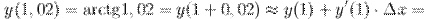

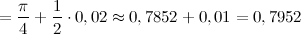
Ответ.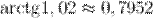

Пример 4. Вычислить значение функции f(x) = ex в точке x=0. 1. Решение. В качестве x0 возьмем число 0, то есть x0=0, тогда ∆ x=x-x0 =0. 1 и e0. 1≈ e0 + e00. 1 = 1+0. 1 = 1. 1. По таблице e0. 1≈ 1. 1052. Ошибка получилась незначительная.

⇐ Предыдущая 12