
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание: изучить материал лекции и выписать примеры применения дифференциала к приближённым вычислениям
Лекция
Задание: изучить материал лекции и выписать примеры применения дифференциала к приближённым вычислениям
Тема урока: Нахождение приближенных значений величин с помощью дифференциала.
Цель: сформировать представление о методах численного дифференцирования.
Ход урока
1. Лекция
Основным инструментом для решения сложных математических задач в настоящее время являются численные методы, позволяющие свести решение задачи к выполнению конечного числа арифметических действий над числами; при этом результаты получаются в виде числовых значений.
Подчеркнем важные отличия численных методов от аналитических. Во-первых, численные методы позволяют получить лишь приближенное решение задачи. Во-вторых, они обычно позволяют получить лишь решение задачи с конкретными значениями параметров и исходных данных. Численные методы незаменимы в сложных задачах, которые не допускают аналитического решения. Многие численные методы разработаны давно, однако при вычислениях вручную они могли использоваться лишь для решения не слишком трудоемких задач. С появлением компьютеров начался период бурного развития численных методов и их внедрения в практику. Только вычислительной машине под силу выполнить за короткое время объем вычислений в миллиарды, триллионы и более операций, необходимых для решения многих современных задач.
Разработкой численных методов занимались крупнейшие ученые своего времени: Ньютон, Эйлер, Лобачевский, Гаусс, Эрмит, Чебышев и др. Численные методы, разработанные ими, носят их имена.
Численный метод наряду с возможностью получения результата за приемлемое время должен обладать и еще одним важным качеством — не вносить в вычислительный процесс значительных погрешностей. Рассмотрим один из численных методов нахождения значений функций с помощью дифференциала.
Для приближенного вычисления значения функции применяется следующая формула:
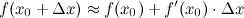
Пример 1. Вычислить приближенно 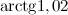 , заменяя приращение функции ее дифференциалом.
, заменяя приращение функции ее дифференциалом.
Решение. Рассмотрим функцию 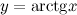 . Необходимо вычислить ее значение в точке
. Необходимо вычислить ее значение в точке 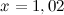 . Представим данное значение в виде следующей суммы:
. Представим данное значение в виде следующей суммы:
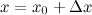
Величины 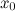 и
и 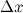 выбираются так, чтобы в точке
выбираются так, чтобы в точке 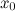 можно было бы достаточно легко вычислить значение функции и ее производной, а
можно было бы достаточно легко вычислить значение функции и ее производной, а 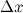 было бы достаточно малой величиной. С учетом этого, делаем вывод, что
было бы достаточно малой величиной. С учетом этого, делаем вывод, что 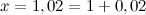 , то есть
, то есть 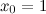 ,
, 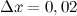 .
.
Вычислим значение функции 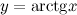 в точке
в точке 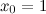 :
:
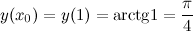
Далее продифференцируем рассматриваемую функцию и найдем значение  :
:
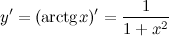
Тогда
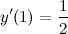
Итак,

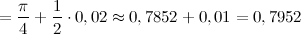
Ответ. 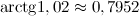
Пример 2. С помощью дифференциала вычислить приближенно 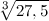
Решение. Для вычисления данного значения применим формулу из теории
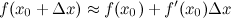
Введем в рассмотрение функцию 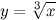 , а заданную величину представим в виде
, а заданную величину представим в виде 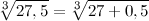 , тогда
, тогда 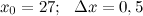
Вычислим 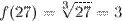
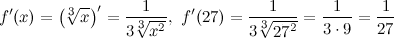
Подставляя все в формулу, окончательно получим
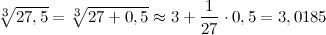
Ответ. 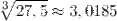
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|