Случайные события. Операции над событиями. Определение вероятности события.

Стр 1 из 2Следующая ⇒

Случайные события. Операции над событиями. Определение вероятности события.

Теория вероятностей – это раздел математики, который изучает закономерности в массовых случайных событиях.

Событие – это факт, который может произойти или не произойти в результате проведения опыта или испытания.

Выделяют три вида событий:

а) достоверные

б) невозможные

с) случайные

Достоверное событие – это событие, которое обязательно произойдёт в результате данного опыта. ( например: при бросании кубика выпадет 1≤ целое число≤ 6).

Невозможное событие – это событие, которое никогда не произойдет в условиях данного опыта. . ( например: при бросании кубика выпадет число≥ 7, например 10).

Случайное событие – это событие, которое может произойти или не произойти в результате данного опыта. ( например: бросили кубик один раз – выпадение числа 3 – случайное событие).

События обозначаются первыми заглавными буквами латинского алфавита: А, В, С, D,.

События называются массовыми, если они происходят одновременно в достаточно большом числе испытаний или многократно повторяются. ( например: много людей бросают кубики или один человек бросает кубик много раз).

Классификация случайных событий.

Равновозможные события – это события такие, что ни одно из них не является более возможным, чем другие ( например: кубику всё равно на какую грань упасть).

Совместные события – это события, которые могут произойти одновременно в результате данного опыта. ( например: бросаем 2 кубика - выпадение числа 1 и выпадение числа 3 – совместные события).

Несовместные события – это равновозможные события такие, что появление одного из них исключает появление остальных. ( например: бросаем 1 кубик – выпадение цифры 3 исключает выпадение остальных цифр).

Несколько случайных событий: А₁, А₂, А₃… А_п, образуют полную группу событий, если каждое из них может произойти в результате данного опыта. ( например: выпадение чисел 1, 2, 3, 4, 5, 6 –полная группа событий для бросания одного кубика).

Противоположные события А и 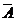– это равновозможные несовместные события, образующие полную группу событий. Появление события А исключает появление события 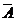(не А). ( например: орёл или решка, попадание в мишень или промах).

Несмотря на то, что события случайные, при большом числе опытов они подчиняются закономерностям, которые изучает теория вероятностей.

12 Следующая ⇒