Пример 2. Пример 3. Пример 4. Пример 6. Пример 7. Пример 8. Пример 9. Пример 10

Задание. Вычислить неопределенный интеграл

Решение. Для решения данного интеграла не нужно использовать свойства неопределенных интегралов, достаточно формулы интеграла степенной функции:

В нашем случае , тогда искомый интеграл равен:

Пример 2

Под интегралом сумма. У нас на этот случай есть свойства линейности. : ) Разбиваем наш интеграл на три отдельных, выносим все константы за знаки интегралов и считаем каждый по таблице (группа 1-2):

Прошу обратить внимание: константа С появляется именно в тот момент, когда исчезают ВСЕ знаки интеграла!

Разумеется, так подробно расписывать обычно не требуется. Это чисто для понимания сделано. Чтобы суть уловить. )

Например, очень скоро, особо не раздумывая, вы в уме будете давать ответ к примерам типа:

Пример 3

Надеюсь, всем понятно, что наше подынтегральное выражение можно расписать вот так:

Подынтегральная функция отдельно, а множитель dx (значок дифференциала) — отдельно.

Замечание: множитель dx в процессе интегрирования пока никак не участвует работаем только с подынтегральной функцией.

А пока посмотрим на подынтегральную функцию

Не очень похоже на степенную функцию, но это она. Если вспомнить школьные свойства корней и степеней, то вполне можно преобразовать нашу функцию:

А икс в степени минус две трети – это уже табличная функция! (n=-2/3). А константу 1/2 выносим за знак интеграла, и прямо по формуле считаем:

В этом примере нам помогли элементарные свойства степеней. И так надо делать в большинстве случаев, когда под интегралом стоят одинокие корни или дроби. Посему пара практических советов при интегрировании степенных конструкций:

1. Заменяем дроби степенями с отрицательными показателями;

2. Заменяем корни степенями с дробными показателями.

А вот в окончательном ответе переход от степеней обратно к дробям и корням – дело вкуса. И, пожалуйста, аккуратно считаем все дроби! Внимательно следим за знаками и за тем, что куда идёт – что в числитель, а что знаменатель.

Пример 4

Если сейчас привести всё под интегралом к общему знаменателю, то можно застрять на этом примере всерьёз и надолго. ) Но, присмотревшись повнимательнее к подынтегральной функции, можно заметить, что наша разность состоит из двух табличных функций. Так что не будем извращаться, а вместо этого разложим наш интеграл на два:

Первый интеграл – обычная степенная функция, ( n = -1), 1/x = x^-1.

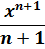Традиционная наша формула для первообразной степенной функции

здесь не работает, но зато у нас для n = -1 есть достойная альтернатива – формула с натуральным логарифмом. Вот эта:

Тогда, согласно этой формуле, первая дробь интегрируется так:

А вторая дробь – тоже табличная функция! Узнали? Да! Это седьмая формула с " высоким" логарифмом:

Константа " а" в этой формуле равна двойке: a=2.

Обратите внимание, константу С при промежуточном интегрировании я нигде не приписываю! Почему? Потому что она пойдёт в окончательный ответ всего примера. Этого вполне достаточно

Пример 5

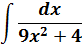
В таблице, понятное дело, такой функции нет. Но зато есть похожая функция:

Вот эта:

И нам нужно подстроить наш интеграл под эту формулу! Но есть одна проблема: в табличной формуле перед х² никакого коэффициента нету, а у нас - девятка. Не можем пока что напрямую воспользоваться формулой. Но в нашем случае проблема вполне решаема. Вынесем эту девятку сначала за скобки, а потом вообще уведём за пределы нашей дроби. )

А новая дробь - уже нужная нам табличная функция под номером 8! Здесь а²=4/9. Или а=2/3.

Всё. Выносим 1/9 за знак интеграла и пользуемся формулой:

Пример 6

В знаменателе появился корень. Естественно, изменилась и соответствующая формула для интегрирования. Опять смотрим в таблицу и ищем подходящую. групп. Но в шестой группе под корнями только разность. А у нас – сумма. Значит, работаем по пятой формуле, с " длинным" логарифмом:

Число А у нас – пятёрка. Подставляем в формулу и получаем:

Пример 7

Под корнем снова минус, но х² с пятёркой поменялись местами. Похоже, но не одно и то же… На этот случай в нашей таблице тоже есть формула.

А вот теперь – аккуратно. В предыдущем примере у нас пятёрка выступала в роли числа A . Здесь же пятёрка будет выступать уже в роли числа а ² !

Поэтому для правильного применения формулы не забываем извлечь корень из пятёрки:

И теперь пример решается в одно действие.

Пример 8

Пример простой. Настолько простой, что народ, даже не глядя в таблицу, тут же ответ пишет и…

Следим за знаками! Это самая распространённая ошибка при интегрировании синусов/косинусов. Не путаем с производными!

Да, (sin x)' = cos x и (cos x)’ = -sin x.

Но!

Приём для запоминания интегралов тут очень простой:

Интеграл от синуса/косинуса = минус производная от тех же синуса/косинуса.

Например, мы ещё со школы знаем, что производная синуса равна косинусу:

(sin x)' = cos x.

Тогда для интеграла от того же синуса будет справедливо:

Исправляем теперь наш пример:

Применение формул тригонометрии

Продолжим развлекаться с тригонометрией.

Пример 9

Такой функции в таблице и близко нет. Зато в тригонометрии есть такое тождество:

Выражаем теперь из него нужный нам квадрат тангенса и вставляем под интеграл:

Зачем это сделано? А затем, что после такого преобразования наш интеграл сведётся к двум табличным и будет браться в уме!

Смотрите:

Пример 10

Что, внушает? Таблица интегралов пока бессильна, да. Но, если снова заглянуть в нашу сокровищницу тригонометрических формул, то можно увидеть весьма полезную формулу косинуса двойного угла:

Вот и применяем эту формулу к нашей подынтегральной функции. В роли " альфа" у нас х/2.

Получаем:

Формулы сокращённого умножения, раскрытие скобок, приведение подобных и метод почленного деления.

12 Следующая ⇒