Контакты

Случайная статья

2. Интегрирование методом замены переменной.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

2. Интегрирование методом замены переменной.

Это переписываем всё!!!

Сущность интегрирования методом замены переменной (способом подставки) заключается в преобразовании интеграла ∫ ƒ (х)dx в интеграл ∫ F(u)du, который легко вычисляется по какой-либо из основных формул интегрирования.

Для нахождения интеграла ∫ ƒ (х)dx заменяем переменную х новой переменной u с помощью подставки х=φ (u). Дифференцируя это равенство, получим dx= φ '(u)du. Подставляя в подынтегральное выражение вместо х и dx их значения, выраженные через u и du, имеем

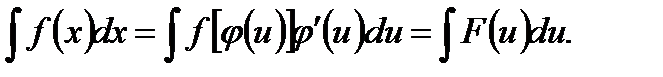
После того как интеграл относительно новой переменной u будет найден, с помощью подставки u= φ (x) он приводится к переменной х.

Пример 1.

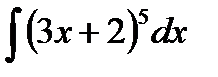
Введем подставку 3х+2=u. Дифференцируем и получаем равенство 3dx=du, откуда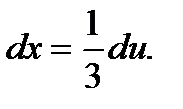

Подставив в данный интеграл вместо 3х+2 и dx их выражения получаем:

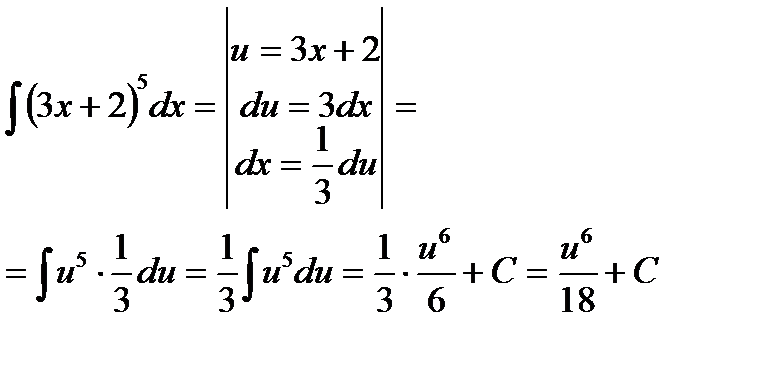
Делая обратную замену находим

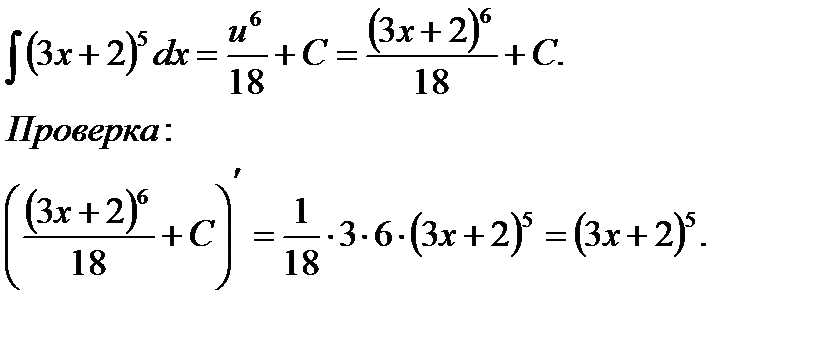
Пример 2.

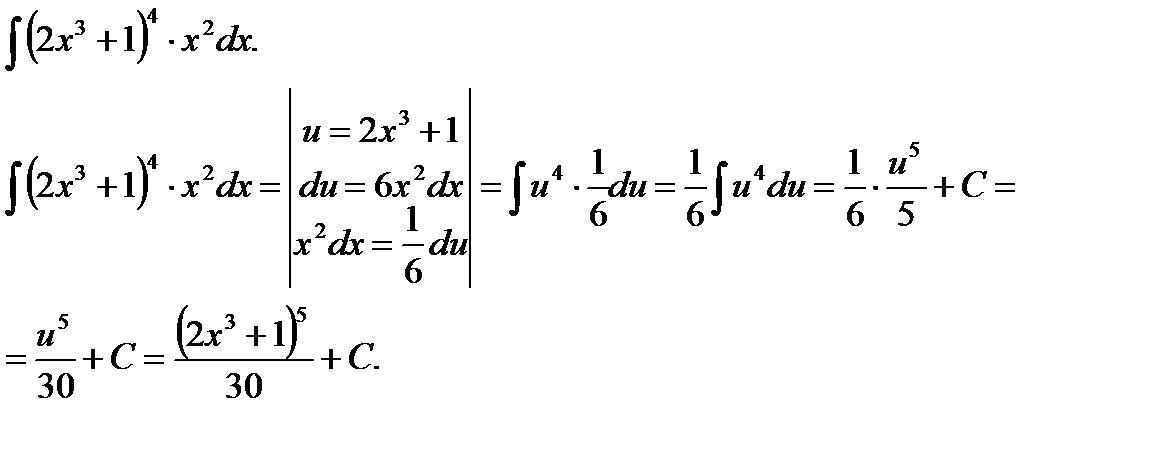
Пример 3.

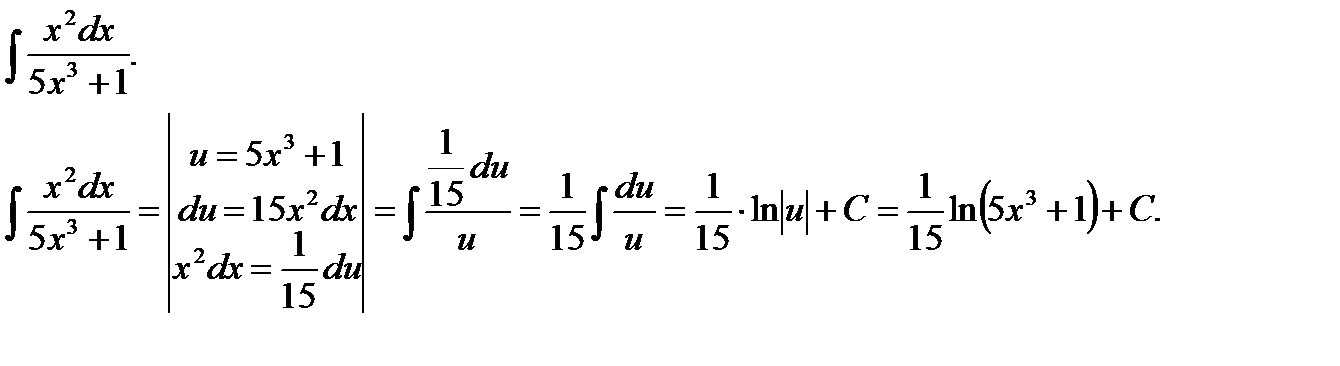
Пример 4.

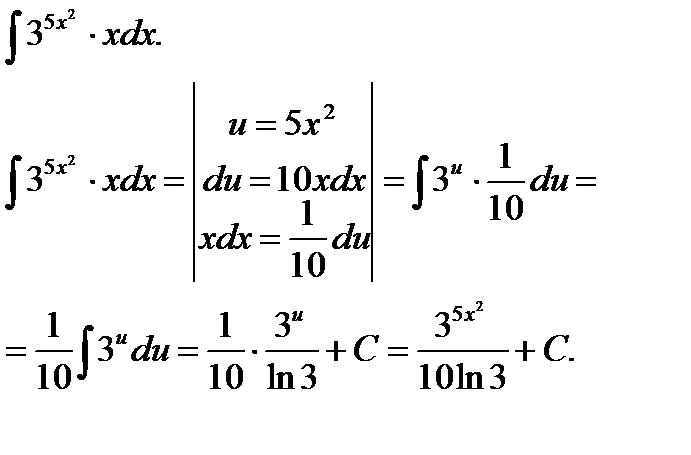
Пример 5.

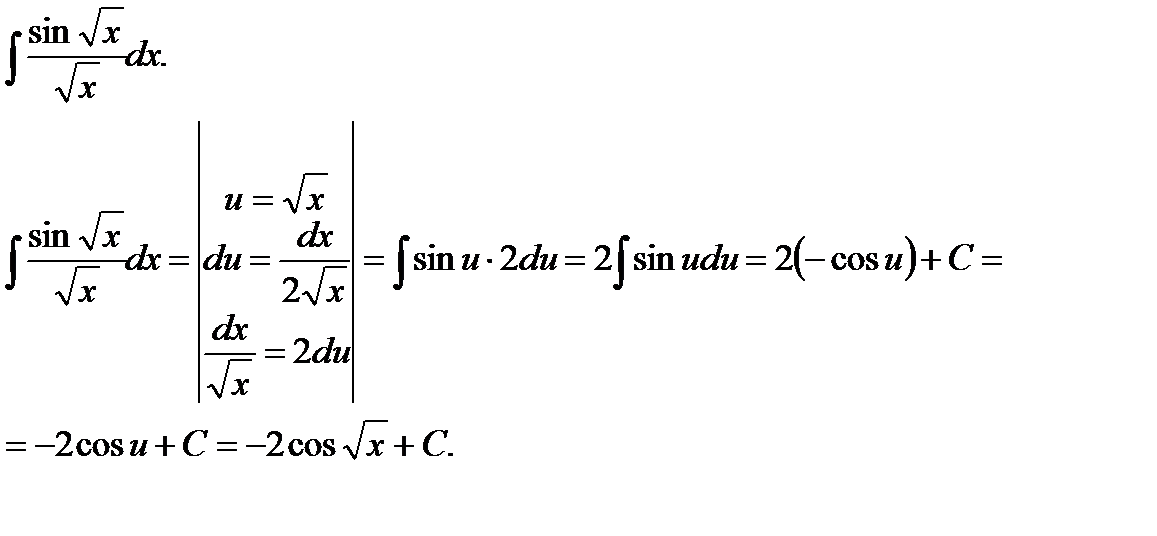
Пример 6.

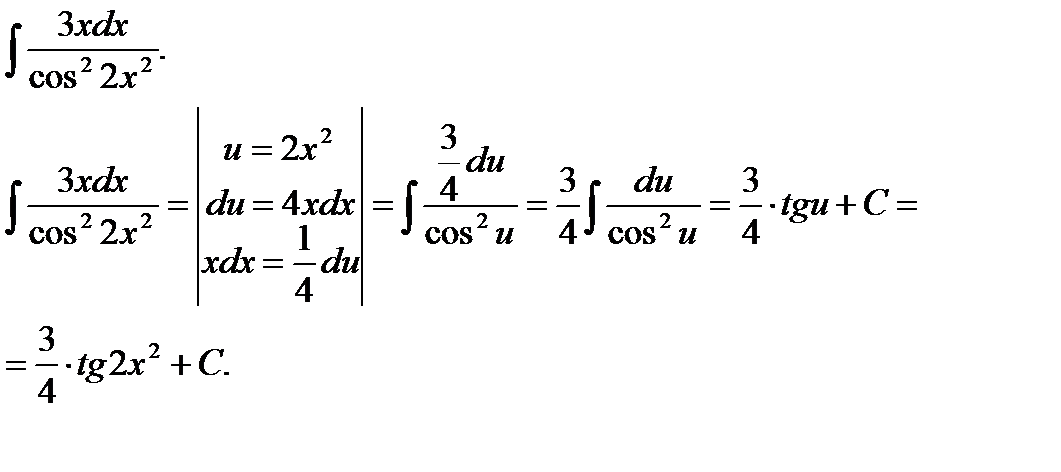
Пример 7.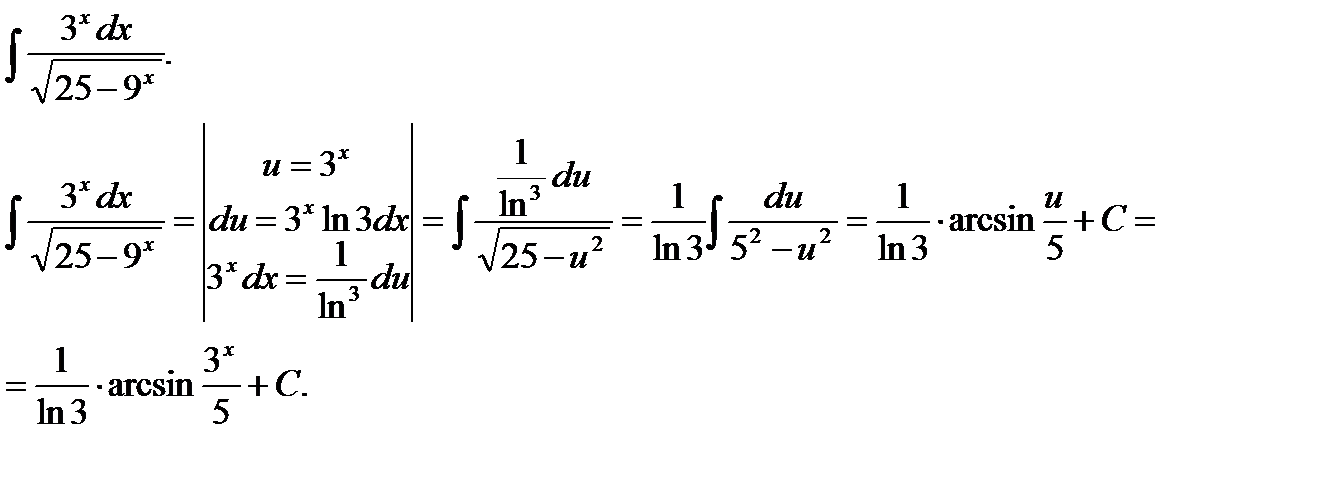

3. Интегрирование по частям

Интегрируя обе части равенства 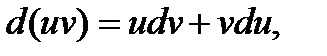получаем

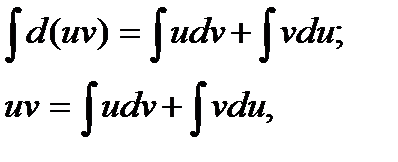
откуда

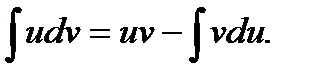
С помощью этой формулы вычисление интеграла 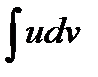сводится к вычислению 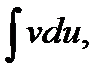если последний окажется проще исходного.

Найти следующие интегралы:

Пример 1.

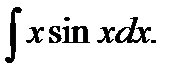
Положим 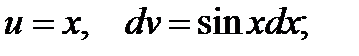тогда, т. е. 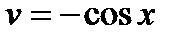Используя формулу, получим

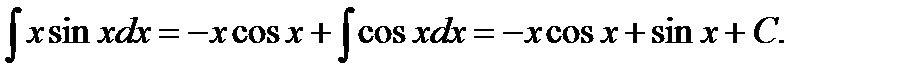
Пример 2.

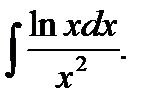
положим

⇐ Предыдущая 123 Следующая ⇒

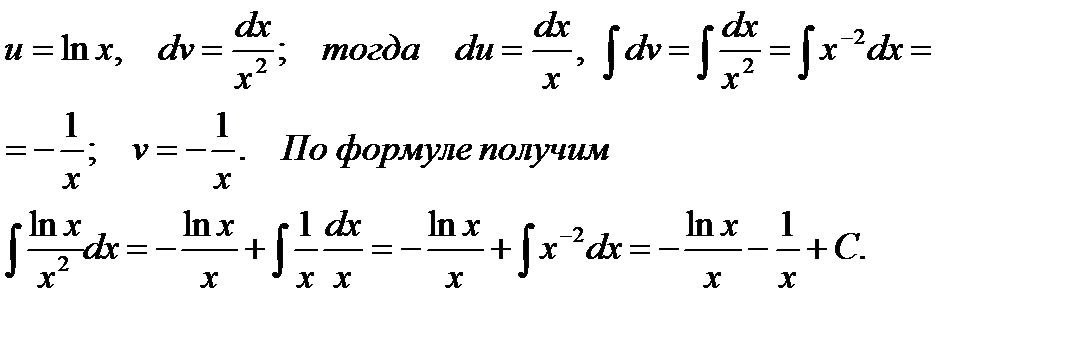
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.