
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
11.2. Задача 10–2.
10 клас
10. 1. Для якого найбільшого натурального 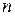 існує набір з
існує набір з 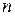 натуральних чисел, який має таку властивість: серед чисел набору рівно одне число ділиться на
натуральних чисел, який має таку властивість: серед чисел набору рівно одне число ділиться на 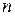 , рівно два числа діляться на
, рівно два числа діляться на 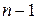 , і так далі, рівно
, і так далі, рівно 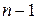 число з цього набору ділиться на 2 і усі
число з цього набору ділиться на 2 і усі 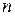 чисел діляться на
чисел діляться на 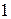 ?
?
(Рубльов Богдан)
Відповідь: 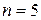 .
.
 Розв’язання. Спочатку наведемо шуканий приклад для
Розв’язання. Спочатку наведемо шуканий приклад для  . Наприклад, умову задовольняють такі числа:
. Наприклад, умову задовольняють такі числа:  .
.
Припустимо такий набір існує при  . Тоді
. Тоді 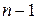 число ділиться на
число ділиться на 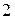 ,
, 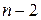 числа діляться на
числа діляться на 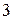 . Тобто максимум одне число не ділиться на
. Тобто максимум одне число не ділиться на 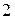 і максимум два не діляться на
і максимум два не діляться на 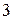 , тому максимум три числа не діляться на
, тому максимум три числа не діляться на 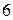 , тому мінімум
, тому мінімум 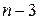 числа кратні
числа кратні 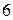 , але за умовою їх повинно бути рівно
, але за умовою їх повинно бути рівно 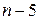 . Одержана суперечність завершує доведення.
. Одержана суперечність завершує доведення.
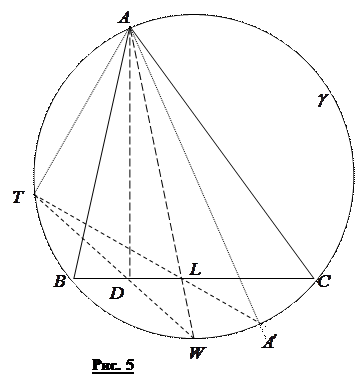
10. 2. Коло 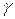 описане навколо гострокутного трикутника
описане навколо гострокутного трикутника 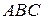 ,
, 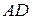 та
та 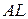 – його висота та бісектриса відповідно. Позначимо через
– його висота та бісектриса відповідно. Позначимо через 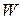 ,
,  ,
, 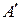 другі точки перетину з колом
другі точки перетину з колом 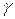 прямих
прямих 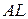 ,
,  ,
,  відповідно. Доведіть, що
відповідно. Доведіть, що 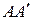 – діаметр кола
– діаметр кола 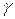 .
.
(Рожкова Марія)
Розв’язання. Якщо 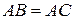 , то твердження очевидне. Інакше, спочатку покажемо, що
, то твердження очевидне. Інакше, спочатку покажемо, що 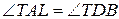 (рис. 5). Дійсно,
(рис. 5). Дійсно,
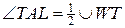 ,
, 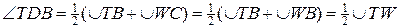
оскільки 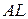 – бісектриса, тому
– бісектриса, тому 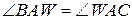 , звідки
, звідки 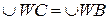 . З доведеної рівності
. З доведеної рівності 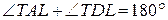 , тому точки
, тому точки  лежать на одному колі. Тоді
лежать на одному колі. Тоді 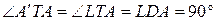 , звідки й випливає потрібне твердження.
, звідки й випливає потрібне твердження.
10. 3. Чи існує геометрична прогресія натуральних чисел 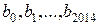 із знаменником відмінним від
із знаменником відмінним від 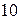 , яка задовольняє таку умову: число
, яка задовольняє таку умову: число 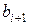 має у своєму десятковому записі рівно на одну цифру більше, ніж число
має у своєму десятковому записі рівно на одну цифру більше, ніж число 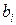 для усіх
для усіх  від 0 до 2013?
від 0 до 2013?
(Рубльов Богдан)
Відповідь . існує.
Розв’язання. Розв’яжемо задачу для довільного скінченого натурального 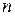 і прогресії
і прогресії 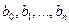 .
.
Виберемо 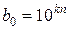 , де натуральний параметр
, де натуральний параметр 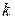 визначимо пізніше, та
визначимо пізніше, та  . Тоді
. Тоді
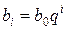
 ,
,  .
.
Для того, щоб виконувались умови задачі, достатньо, щоб 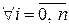 виконувалась умова:
виконувалась умова:
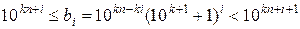 .
.
Спочатку покажемо, що ліва нерівність справджується 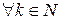 , дійсно
, дійсно
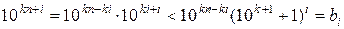 .
.
Тепер знайдемо за яких умов може справджуватись права нерівність.

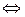
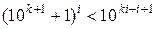
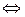

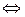

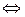
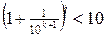 .
.
Якщо вибрати 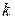 , що задовольняє умову
, що задовольняє умову 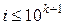 , то будемо мати таку нерівність:
, то будемо мати таку нерівність:
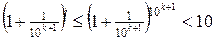 .
.
Для її доведення, якщо не використовувати властивості послідовності  , можна провести такі міркування при
, можна провести такі міркування при 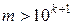 :
:
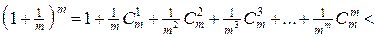
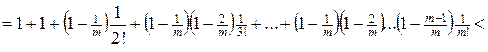
 .
.
Таким чином, щоб ця нерівність справджувалась 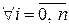 , треба щоб виконувалась нерівність
, треба щоб виконувалась нерівність  . Це є достатньою умовою для вибору потрібного значення
. Це є достатньою умовою для вибору потрібного значення 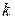 .
.
Тепер повернемось до початкової задачі, у якій  . Достатньо обрати
. Достатньо обрати  . Оскільки
. Оскільки 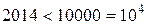 , то для прогресії з нульовим членом
, то для прогресії з нульовим членом  та знаменником
та знаменником 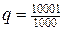 виконуються потрібні умови.
виконуються потрібні умови.
Альтернативне розв’язання. Нехай, як і раніше, 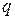 – знаменник прогресії. Нехай для деякого натурального
– знаменник прогресії. Нехай для деякого натурального 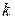 виконується умова:
виконується умова: 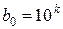 . Для існування шуканої прогресії достатньо існування такого
. Для існування шуканої прогресії достатньо існування такого 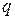 , щоб виконувались умови:
, щоб виконувались умови:
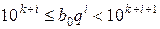 ,
, 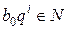 ,
, 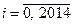 . (1)
. (1)
Тоді, з урахуванням значення 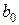 , першу умову можна записати таким чином:
, першу умову можна записати таким чином:
 або
або  ,
, 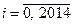 . (2)
. (2)
Підберемо 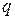 таким, що задовольняє умову
таким, що задовольняє умову 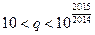 . Тоді автоматично виконуються умови (2), оскільки
. Тоді автоматично виконуються умови (2), оскільки 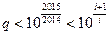
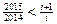 , а остання нерівність для натуральних
, а остання нерівність для натуральних  просто перевіряється. Для цього достатньо знаменник прогресії
просто перевіряється. Для цього достатньо знаменник прогресії 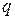 шукати у такому вигляді:
шукати у такому вигляді:
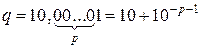 .
.
 Зрозуміло, що таке
Зрозуміло, що таке 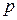 існує, бо
існує, бо 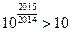 , а
, а 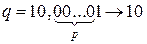 при
при 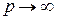 , тому знайдеться шукане значення
, тому знайдеться шукане значення 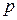 .
.
Тепер залишається досягти умови натуральності членів прогресії, тобто 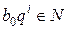 , тут достатньо вибрати
, тут достатньо вибрати  .
.
Твердження доведене.
10. 4. Нехай є зв’язний граф з вершинами  . Позначимо
. Позначимо  – найменшу кількість ребер, які необхідно пройти, щоб дістатися з вершини
– найменшу кількість ребер, які необхідно пройти, щоб дістатися з вершини 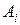 у вершину
у вершину  . Знайдіть найбільше можливе значення суми:
. Знайдіть найбільше можливе значення суми: 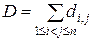 .
.
Відповідь . 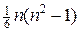 .
.
Розв’язання. Розглянемо такий граф, що має максимальне значення 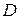 (або один з таких графів). Якщо в цьому графі є цикл, то вилучимо з нього ребро, граф залишиться зв’язним, а величина
(або один з таких графів). Якщо в цьому графі є цикл, то вилучимо з нього ребро, граф залишиться зв’язним, а величина 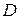 принаймні не зменшується. Продовжуючи таким чином, одержимо зв’язний граф без циклів, тобто дерево. Відомо, що в такому графі знайдеться хоча б дві висячі вершини (тобто вершини степінь яких дорівнює 1).
принаймні не зменшується. Продовжуючи таким чином, одержимо зв’язний граф без циклів, тобто дерево. Відомо, що в такому графі знайдеться хоча б дві висячі вершини (тобто вершини степінь яких дорівнює 1).
 Позначимо дві висячі вершини
Позначимо дві висячі вершини  та
та 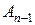 . Нехай
. Нехай

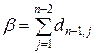 .
.
Позначимо  . Перемалюємо граф таким чином, як показано на рис. 6. Обчислимо, як зміниться при цьому значення
. Перемалюємо граф таким чином, як показано на рис. 6. Обчислимо, як зміниться при цьому значення 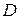 .
.
 .
.
Оскільки 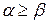 , тo
, тo 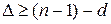 . І якщо тепер
. І якщо тепер  , то ми можемо збільшити
, то ми можемо збільшити 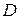 . Але нескінченно довго ми не можемо збільшувати
. Але нескінченно довго ми не можемо збільшувати 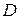 , то ми прийдемо до випадку
, то ми прийдемо до випадку 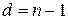 , але тоді граф – ланцюг рис. 7. Тому
, але тоді граф – ланцюг рис. 7. Тому 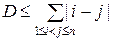 і це значення досягається на ланцюгу. Залишається його обчислити:
і це значення досягається на ланцюгу. Залишається його обчислити:
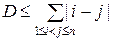
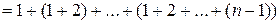
 .
.
11 клас
11. 1. Знайдіть усі значення параметру 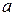 , при яких нерівність
, при яких нерівність
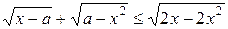
має єдиний розв’язок у дійсних числах.
(Рубльов Богдан)
Відповідь:  .
.
Розв’язання. Якщо позначити три вирази
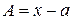 ,
,  та
та 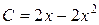 ,
,
то з умов задачі маємо такі дві умови:
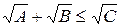 та
та 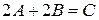 .
.
Після піднесення до квадрату нерівності одержимо, що
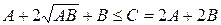
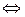
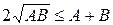 .
.
Остання нерівність виконується при усіх можливих значеннях 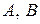 . Таким чином розв'язком нерівності є її ОДЗ. Воно задається такими трьома нерівностями:
. Таким чином розв'язком нерівності є її ОДЗ. Воно задається такими трьома нерівностями:
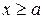 ,
, 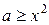 та
та 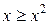 .
.
Зрозуміло, що 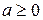 , крім того справджується умова:
, крім того справджується умова: 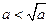
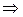
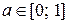 . За таких значень параметра
. За таких значень параметра 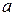 розв’язком нерівності є множина
розв’язком нерівності є множина 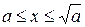 , таким чином єдиний розв’язок цієї нерівності буде за умови
, таким чином єдиний розв’язок цієї нерівності буде за умови  , тобто
, тобто  .
.
11. 2. Задача 10–2.
11. 3. Для яких натуральних 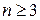 існує набір прямокутників
існує набір прямокутників 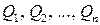 , які мають таку властивість: будь-який з цих прямокутників можна покрити усіма іншими
, які мають таку властивість: будь-який з цих прямокутників можна покрити усіма іншими 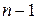 -м прямокутником з цього набору, але не можна покрити ніякими
-м прямокутником з цього набору, але не можна покрити ніякими 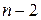 -ма іншими прямокутниками з цього набору? (Прямокутники можна розташовувати в будь-якому з двох положень, при яких їх сторони є паралельними двом заданим перпендикулярним прямим).
-ма іншими прямокутниками з цього набору? (Прямокутники можна розташовувати в будь-якому з двох положень, при яких їх сторони є паралельними двом заданим перпендикулярним прямим).
Відповідь: Для довільного 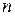 .
.
Розв’язання. Нехай прямокутники мають розміри 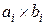 ,
, 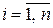 . Для виконання умови необхідно, щоб сторони прямокутників задовольняли нерівностям:
. Для виконання умови необхідно, щоб сторони прямокутників задовольняли нерівностям: 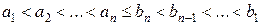 .
.
Покажемо далі, що достатньо щоб вони задовольняли такі умови:
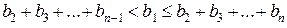 , (1)
, (1)
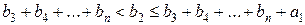 , (2)
, (2)
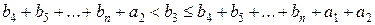 ,
,
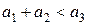 ,
,
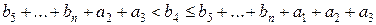 ,
,
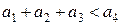 ,
,
.........................
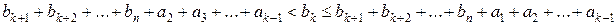 , (3)
, (3)
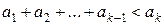 , (4)
, (4)
.........................

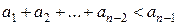
 . (5)
. (5)
Пара нерівностей (3), (4)  гарантує, що прямокутник
гарантує, що прямокутник 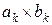 не вдасться покрити менш ніж
не вдасться покрити менш ніж  -м прямокутником, а
-м прямокутником, а  -м – вдасться. Пояснимо, чому це так. Будемо говорити, що прямокутник розташовано горизонтально, якщо його горизонтальна сторона не коротша за вертикальну, й вертикально у протилежному випадку. Будемо вважати, що прямокутник
-м – вдасться. Пояснимо, чому це так. Будемо говорити, що прямокутник розташовано горизонтально, якщо його горизонтальна сторона не коротша за вертикальну, й вертикально у протилежному випадку. Будемо вважати, що прямокутник 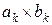 розташовано горизонтально. Тоді прямокутниками, що залишилися його можна покрити наступним чином (рис. 8). З іншого боку, меншої кількості прямокутників не вистачить. Дійсно, якщо якісь з прямокутників
розташовано горизонтально. Тоді прямокутниками, що залишилися його можна покрити наступним чином (рис. 8). З іншого боку, меншої кількості прямокутників не вистачить. Дійсно, якщо якісь з прямокутників 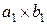 , …,
, …,  розташовувати не вертикально, а горизонтально, то довжин їх вертикальних сторін не вистачить, щоб покрити вертикальну сторону прямокутника
розташовувати не вертикально, а горизонтально, то довжин їх вертикальних сторін не вистачить, щоб покрити вертикальну сторону прямокутника 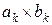 , оскільки справджується нерівність (4), а тоді всередині нього непокритою все одно залишиться деяка смужка довжиною
, оскільки справджується нерівність (4), а тоді всередині нього непокритою все одно залишиться деяка смужка довжиною  , яку іншими прямокутниками покрити не вдасться. А тоді, максимальна сума горизонтальних сторін буде як раз
, яку іншими прямокутниками покрити не вдасться. А тоді, максимальна сума горизонтальних сторін буде як раз
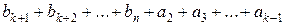 ,
,
що за умовою (3) менше ніж  .
.
Набір прямокутників, що задовольняє нашим нерівностям, можна побудувати наступним чином. Спочатку послідовно обираємо 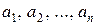 так, щоб виконувались нерівності (4) при усіх
так, щоб виконувались нерівності (4) при усіх  й
й 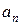 з умови (5). Далі виберемо
з умови (5). Далі виберемо 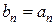 , після чого послідовно будемо обирати числа
, після чого послідовно будемо обирати числа 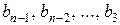 так, щоб вони задовольняли нерівностям (3) при
так, щоб вони задовольняли нерівностям (3) при 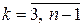 , а далі число
, а далі число 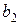 , що задовольняє умову (2) та число
, що задовольняє умову (2) та число 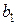 з нерівності (1).
з нерівності (1).
11. 4. Чи для довільної скінченної підмножини 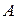 натуральних чисел існує просте число
натуральних чисел існує просте число 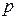 таке, що для кожного числа
таке, що для кожного числа 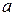 , що належить
, що належить 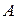 , знайдеться натуральне число
, знайдеться натуральне число 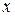 таке, що
таке, що 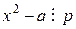 , але
, але 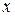 не ділиться націло на
не ділиться націло на 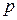 ?
?
(Ківва Богдан).
Відповідь . так, для довільної.
Розв’язання. Покажемо, що для довільної скінченної підмножини існує потрібне 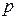 . Нехай
. Нехай 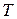 – множина всіх тих простих чисел, які є дільниками хоча б одного числа з
– множина всіх тих простих чисел, які є дільниками хоча б одного числа з 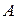 . Так, як множина
. Так, як множина 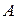 – скінченна, то
– скінченна, то 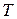 – теж скінченна. За теоремою Діріхле існує просте число вигляду
– теж скінченна. За теоремою Діріхле існує просте число вигляду 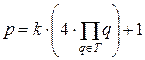 . Покажемо, що це просте число нам підходить.
. Покажемо, що це просте число нам підходить.
З визначення 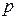 випливає, що для довільного
випливає, що для довільного 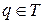 символ Лежандра
символ Лежандра 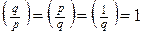 .
. 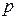 дає остачу
дає остачу 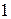 по модулю
по модулю  , тому перша частина рівності слідує з квадратичного закону взаємності Гауса, а друга з того, що
, тому перша частина рівності слідує з квадратичного закону взаємності Гауса, а друга з того, що 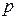 дає остачу
дає остачу 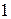 по модулю
по модулю 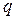 . Отже, кожне просте число з множини
. Отже, кожне просте число з множини 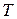 є квадратичним лишком по модулю
є квадратичним лишком по модулю 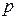 . Але ж кожен елемент з
. Але ж кожен елемент з 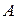 є добутком якихось елементів з
є добутком якихось елементів з 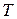 , тому сам є квадратичним лишком, а це і вимагалося від
, тому сам є квадратичним лишком, а це і вимагалося від 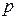 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|