9.1. Задача 8–2.

Перший день

8 клас

8. 1. Відомо, що до натурального числа 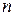можна дописати справа будь-яку ненульову цифру 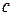і одержане число буде ділитися націло на 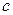. Знайдіть найменше значення, яке може приймати число .

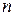(Рубльов Богдан)

Відповідь: .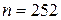

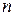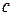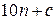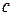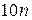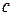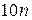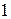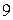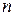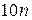Розв’язання. Помітимо, що якщо к числу дописати справа цифру , то ми отримаємо число . Для того, щоб це число ділилось на , необхідно й достатньо, щоб ділилося на . Тобто, для того, щоб виконувалась умова необхідно, щоб ділилося на всі натуральні число від до . Для будь-якого натурального число буде ділитися н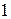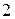а , та . Для подільності на інші цифри, треба щоб число 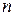ділилося на , та 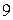. Але тоді воно повинно ділитись на 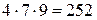, тому менше ніж 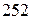число 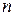бути не може. Нескладно переконатися, що число 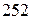умову задовольняє, а тому є шуканим.

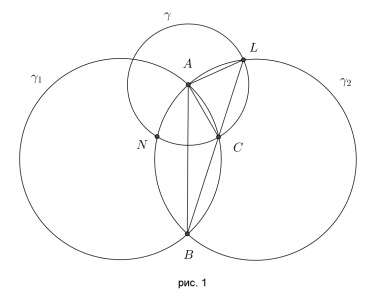
8. 2. Два кол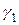а та 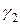однакового радіуса перетинаються у точках 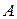та 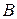. Коло 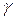, з центром у точці 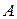, перетинає коло 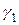у точках 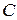та 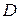. Доведіть, що точки перетину кіл 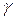та 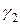належать прямим 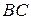та .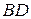

(Білецький Юрій)

Розв’язання. Позначимо через 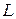та 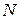точку перетину 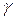та 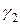(рис. 1). Тоді очевидно, що , оскільки це радіуси кола 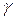. Оскільки кол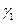а та 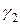мають однаковий радіус, то вписані кути 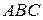та цих кіл спираються на однакові хорди, тому вони є рівними. З рівності цих кутів і випливає твердження задачі.

8. 3. Чи існують натуральні числа 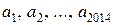, для яких справджується рівність:

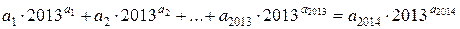(Рубльов Богдан)

Відповідь: таких чисел не існує.

Розв’язання. Без обмеження загальності можемо вважати, що 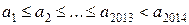, звідки випливає, що 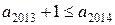. Тому

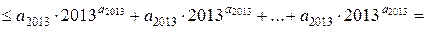
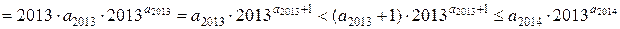Звідси й випливає, що таких наборів не існує.

8. 4. а) Чи можна обійти клітчасту дошку ходом шахового коня таким чином, щоб побувати на кожному полі рівно 1 раз?

б) Чи можна при цьому це зробити так, щоб з останнього поля можна було ходом коня попасти на початкове?

Шаховий кінь може піти на будь-яке поле дошки якщо воно розташоване на іншому кінці української літери „Г”, тобто спочатку кінь пересувається на дві клітини по горизонталі чи по вертикалі, а далі на одну клітину перпендикулярно початковому напряму).

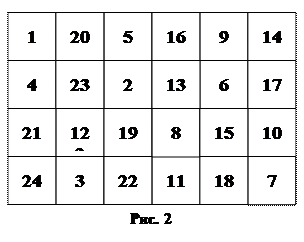
Відповідь: а) можна; б) не можна.

Розв’язання. а) Шуканий приклад наведений на рис. 2.

б) Доведемо методом від супротивного. Припустимо відповідний обхід існує. Розфарбуємо клітини дошки у 4 кольори, як це показано на рис. 3. Позначимо кольори – Б (білий), Ч (чорний), Т (темно сірий) та С (світло сірий). Клітин кожного кольору по 6. Бачимо, що з клітини Ч можна попасти лише у клітину С, а також у клітину Ч можна попасти тільки з клітини С. Аналогічно пов’язані кольори Б та Т: з клітин Б можна попасти тільки на клітини Т, а також на Б можна попасти лише з Т. Випишемо ланцюжок ходів, який обходить дошку потрібним чином, тоді буква Ч повинна оточуватись з обох боків буквами С, так само для букв Б, які повинні оточуватись буквами Т, при умові, що це не перша чи остання клітина маршруту. Оскільки кожної з букв на дошці рівна кількість, то кожна буква Ч не може бути не крайньою, бо тоді 6 літер Ч повинні оточуватись принаймні 7 буквами С, а їх усього 6. Таким чином – Ч та Б повинні бути крайніми у цьому ланцюгу. За припущенням з останньої клітини можна попасти на першу, але якщо вони мають кольори Ч та Б – це неможливе. Одержана суперечність завершує доведення.

9 клас

9. 1. Задача 8–2.

9. 2. Андрій та Олеся грають у таку гру. Спочатку Андрій розставляє по колу усі 10 цифр. Після цього Олеся вибирає цифру, і від цієї цифри рухається по колу за рухом годинникової стрілки, групуючи послідовно цифри по 2. Таким чином утворюються 5 двоцифрових чисел (число на кшталт 06 також враховуємо як одноцифрове число 6). Після цього Олеся додає ці 5 чисел і виграє одержану суму у Андрія. Який найменший програш може гарантувати собі Андрій?

(Рубльов Богдан)

Відповідь: .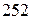

Розв’язання. Після того, як Андрій виставить свої 10 цифр по колу, у Олесі є два варіанти обрати п’ятірку чисел. Наприклад, якщо по колу у порядку за годинниковою стрілкою записані такі цифри: 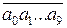, то вона може обрати одну з двох сум:

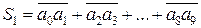або .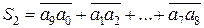

Зрозуміло, що вона обере більше значення з двох.

Тепер зауважимо, що

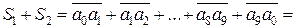
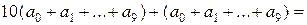
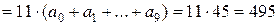Таким чином сума цих двох варіантів однакова. Оскільки вона обирає більше з цих чисел, то Андрій повинен таким чином розставити цифри, щоб різниця між цими числами була найменшою з можливих. Тоді найбільше з двох чисел і буде найменшим.

Тепер побачимо, що

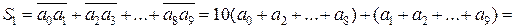
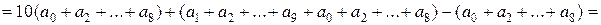
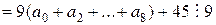Тобто, кожна з сум кратна 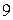, а тому їх мінімальна різниця так само повинна бути кратною 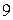. Оскільки сума цих чисел непарна, то рівними вони не можуть бути, тому найменша можлива різниця між ними – це 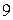. Тобто ці числа повинні дорівнювати 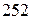та .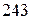

Таким чином, залишається навести приклад розстановки чисел, щоб саме такі два числа могла одержати Олеся. Оскільки 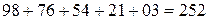, то по колу Андрій може розставити числа, наприклад, таким чином: .

9. 3. Нехай 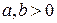дійсні числа. Відомо, що 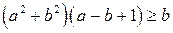. Доведіть, що .

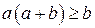(Сердюк Назар)

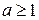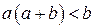Розв’язання. Очевидно, що при нерівність виконується. Нехай і припустимо, що . В такому випадку 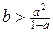. Доведемо, що початкова нерівність не виконується. Якщо вона правильна, то

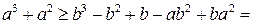
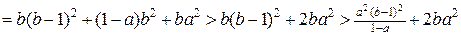Оскільки 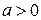, то

, ,

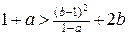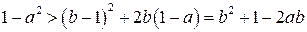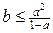звідки – суперечність. Отже, , що і треба було довести.

9. 4. Яку найбільшу кількість кутиків з трьох клітинок (рис. 4) можна розмістити всередині клітчастого квадрата 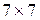так, щоб вони попарно не дотикалися сторонами? (Дотикання кутами припускається. )

(Чорний Максим)

Відповідь: .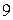

Розв’язок. Приклад для 9 кутів зображено на рис. 5.

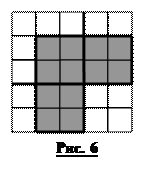
Доведемо, що більшу кількість кутів розмістити не вдасться. Припустимо, що ми розмістили 10 кутиків так, щоб вони задовольняли умові. Розглянемо кожен з них. Пофарбуємо наступні відрізки, як це показано на рис. 6 – тут сторону маленького квадрату вважаємо рівною 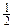, тобто ми одиничні квадрати розбили навпіл на 4 менших рівних квадратики.

Для кожного з кутиків загальна довжина пофарбованих відрізків складає 11, тому їх загальна довжина складає 110. При цьому, як легко зрозуміти, в жодної пари кутиків немає спільних пофарбованих відрізків, але відрізки можуть виходити за межі квадрату (а саме ті, що йдуть з середніх сторін).

Тепер розглянемо одну з сторін великого квадрату. Пофарбуємо на ній всі відрізки, які не належать сторонам кутиків – їх загальна довжина як мінімум 2, що неважко зрозуміти з того, що кутики не можуть дотикатися сторонами, а їх найбільша сторона дорівнює 2; очевидно, що вони не були пофарбовані раніше. Також зітремо всі відрізки, які виходять з середин двоклітинних сторін кутиків і виходять за межі квадрата, причому один кінець яких лежить на цій стороні квадрата – оскільки таких кутиків для даної сторони не більше 2, то загальна довжина стертих відрізків буде не більше 1. Таким чином, сумарна довжина відрізків зросла не менш, ніж на 1. Оскільки є всього 4 сторони квадрата, то вона зросла мінімум на 4 і стала мінімум 114. Але всі відрізки тепер йдуть по лініям сітки квадрата, не співпадають і не виходять за його межі. Але у такому випадку їх довжина не може бути більше за сумарну довжину всіх ліній сітки квадрата, а саме . Суперечність.

⇐ Предыдущая 123 Следующая ⇒