
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
§7 Правило Лопиталя.. Замечания. Примеры. Контрольная Работа по теме «Дифференцирование».. 1. Найти f’(x) производную композиции функций.. 2. Найти производную функции (1+f(x))g(x) (1∞).. 3. Вычислить предел (правило Лопиталя).. 4. Для заданной функ
§7 Правило Лопиталя.
Пусть функции f(x) и g(x) –бесконечно малые при x→ a исуществуют f’(a), g’(a).
При x→ a по формуле Тейлора (ф. Т):
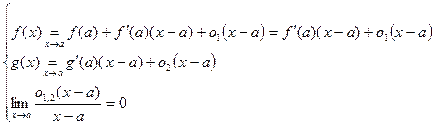
Лемма
Если для бесконечно малых при x→ a функций f(x) и g(x)существуют f’(a), g’(a) и g’(a)≠ 0, то
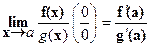
Доказательство:
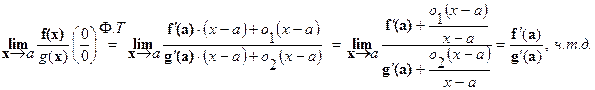
Утверждение (Правило Лопиталя)
Если для б. малых или б. больших при х→ а функций f(x), g(x)существует предел отношения их производных и в некоторой ПО(а, r> 0) g’(x)≠ 0, предел отношения
этих функций равен пределу отношения их производных:
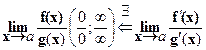
Замечания
1. Правило Лопиталя может быть «продолжено»:
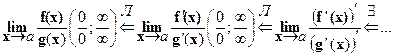
3. Прежде, чем использовать правило Лопиталя, рекомендуется упростить дробь -«вынести за знак предела»конечные и не равные нулю/∞ пределы функций-множителей.
Примеры

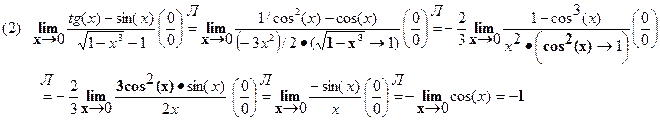
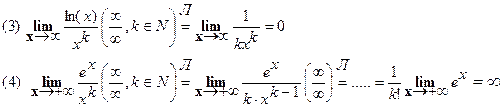
Из (3, 4) следует, что при х→ ∞
- экспонента ex возрастает быстрее любой степенной функции,
- логарифмическая функция ln(x) возрастает медленнее любой степенной функции.
Контрольная Работа по теме «Дифференцирование».
1. Найти f’(x) производную композиции функций.
2. Найти производную функции (1+f(x))g(x) (1∞ ).
3. Вычислить предел (правило Лопиталя).
4. Для заданной функции f(x) и заданной точке x0: (а) записать формулу и полином Тейлора 1 порядка, уравнение касательной прямой; (б) вычислить приближенное значение функции в точке x=x0-0. 1.
Пример. 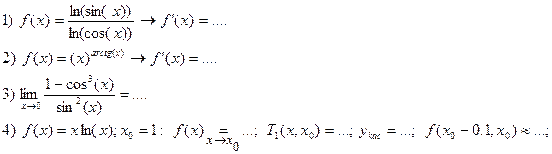
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|