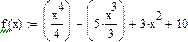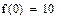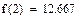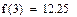- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
§6 Локальные экстремумы функции. Необходимое и достаточное условия.
§6 Локальные экстремумы функции. Необходимое и достаточное условия.
Пусть функция f: Df⊂ R→ R, f(x) определена в O(a, r> 0) и непрерывна в точке а:
f(x→ a)→ f(a)
Определения (1)Точка аназывается точкой локального экстремума (минимума/максимума) непрерывной функции f, если в некоторой ПО(а, r> 0)выполняется неравенство f(x)> f(a) /f(x)< f(a).
XЛЭ=а ó ∃ r> 0∀ x∊ ПО(а, r)∩ Df: f(x)> f(a) ⋁ f(x)< f(a).
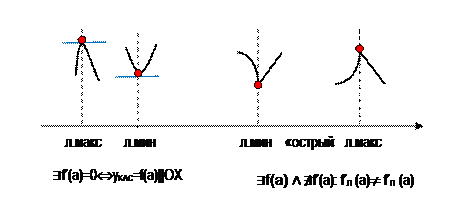
(2) Точка а∊ Df называется стационарной точкой функции, если f’(a)=0 (yKAC=f(a) ||OX),
и называется критической точкой функции, если f’(a)=0 или Ɇ f’(a).
Следствия (Необходимый признак ЛЭ).
1) Непрерывная функция достигает локального экстремума (ЛЭ) только в критической точке:
fнепр(а)= 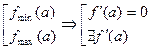
2) Дифференцируемая функция достигает локального экстремума (ЛЭ) только в стационарных точках: fдифф. (а)= 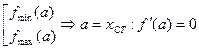
Замечание Необходимый признак не является достаточным признаком ЛЭ: не всякая
критическая точка является точкой локального экстремума функции 
Теорема ( Достаточный признак л. экстремума )
« Если функция f: (1) непрерывна в точке а , (2) дифференцируема в проколотой окрестности этой точки 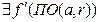 и (3) f '( x< a)∙ f' (x> a) < 0 - производная функция «меняет знак при переходе через точку”, то точка х=а является точкой локального экстремума.
и (3) f '( x< a)∙ f' (x> a) < 0 - производная функция «меняет знак при переходе через точку”, то точка х=а является точкой локального экстремума.
Доказательство. Пусть, например, 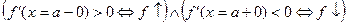
Из формулы Лагранжа f(x) =f(a) + f'(c)(x-a); сÎ (x; a) следует:
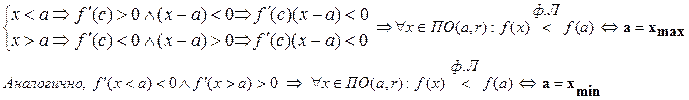
| ПРИМЕРЫ |
|
|
|
|
|
|
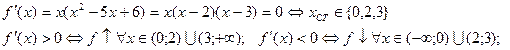

2)
|
|
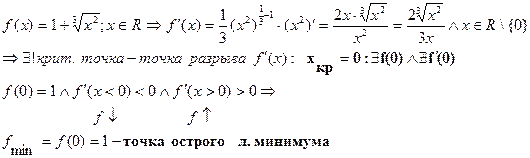
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|