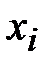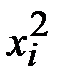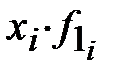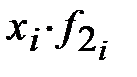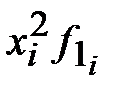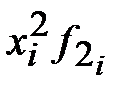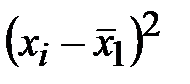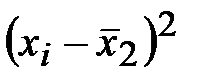Хелпикс

Главная

Контакты

Случайная статья



Решение. 

⇐ ПредыдущаяСтр 2 из 2


Среднее линейное отклонение вычисляется, как среднее арифметическое из абсолютных значений отклонений отдельных вариант от их среднего арифметического:

.

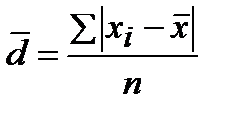Составим вспомогательную таблицу для промежуточных расчётов:

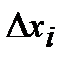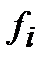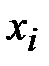
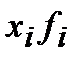
урожайность (цент. с 1 га) посевная площадь (га) середины интервалов произведения отклонения вариант от среднего арифметического 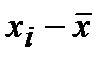абсолютные значения отклонений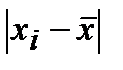
             
             
             
             
             
             
             
             
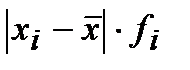
Итого            

 

Тогда:   

                                                  

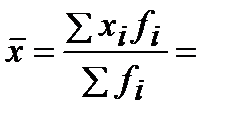
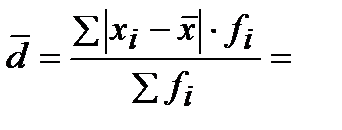
Задача 3 . Распределение рабочих по общему стажу работы составило:

Стаж работы (лет)

Число рабочих
1 цех  2 цех
     
     
     
     
     
     
Итого:    

 

Вычислите: 1) среднюю из групповых дисперсий; 2) межгрупповую дисперсию; 3) общую дисперсию, используя правило сложения дисперсий.

Решение. Будем находить дисперсию двумя способами. Для упрощения расчётов построим вспомогательные таблицы, куда занесём середины интервалов, соответствующих стажу работы, их квадраты и прочие результаты промежуточных вычислений.

Стаж работы  (лет)

середины интервалов

Число рабочих

1 цех ( 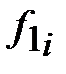) 2 цех ( )
                 
                 
                 
                 
                 
                 
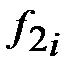Итого: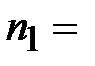            

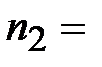
Групповые средние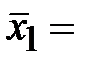

        

 

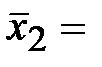
Стаж работы  (лет)

середины интервалов

Число рабочих

1 цех ( 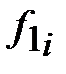) 2 цех ( )
               
               
               
               
               
               
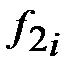Итого: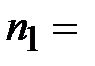          

 

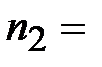
1) Рассчитаем групповые дисперсии. Очевидно, что сначала нам нужно найти средние арифметические по двум группам (обратите внимание, значения сумм у нас уже есть, в таблице! ):

                 

 

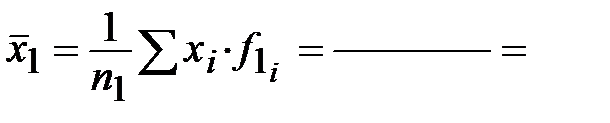
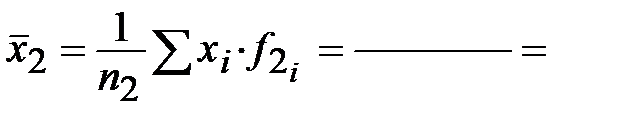
Тогда дисперсия для первой группы:

                         

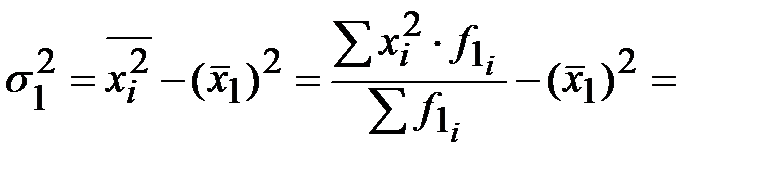
 или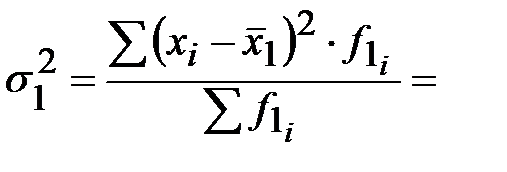 

 

Как видим, результаты совпали.

 

Дисперсия для второй группы:

                         

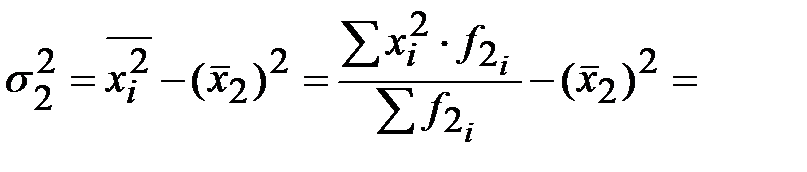
 или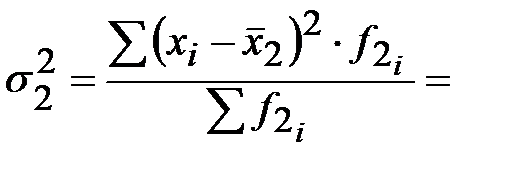 

 

Результаты совпали.

 

Средняя из групповых дисперсий рассчитывается, как

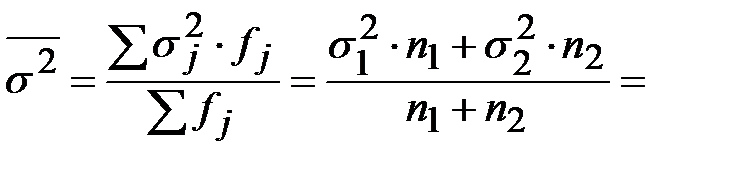
2) Межгрупповую дисперсию найдём по формуле ,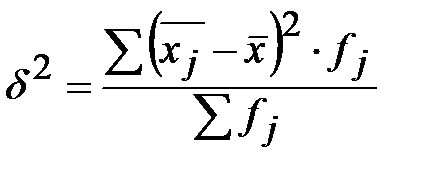  

где

Тогда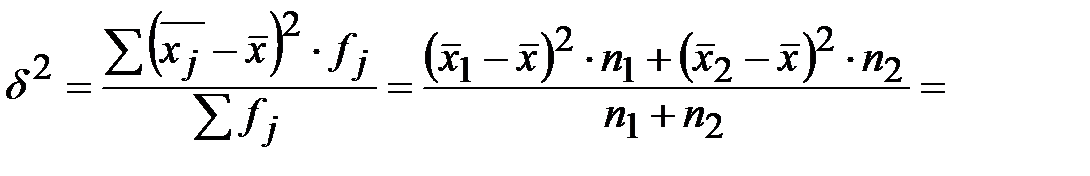

 

3) Общую дисперсию вычислим, используя правило сложения дисперсий:

 

 


⇐ Предыдущая12
  

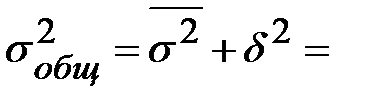
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.