Тема 4. Показатели вариации

Задача 1. Имеются следующие результаты рабочих за смену:

Табельные номера рабочих
Количество изготовленных деталей

Вычислить: 1) среднюю выработку одного рабочего; 2) среднее линейное отклонение; 3) дисперсию; 4) коэффициент вариации; 5) коэффициент осцилляции; 6) относительное линейное отклонение.

Решение. 1)Средняя выработка на одного рабочего может быть вычислена, как средняя арифметическая простая:

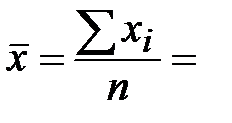
где 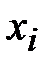– количество изготовленных деталей, п =_____ – общее число рабочих.

2) Среднее линейное отклонение вычисляется, как среднее арифметическое из абсолютных значений отклонений отдельных вариант от их среднего арифметического:

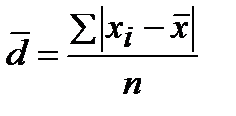Составим вспомогательную таблицу для промежуточных расчётов:

Количество изготовленных деталей ( )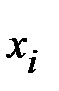

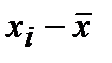
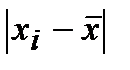
Тогда:

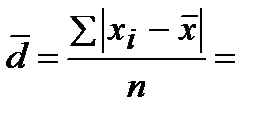
3) Будем вычислять дисперсию, как 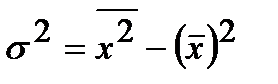. Составим ещё одну вспомогательную таблицу:

Количество изготовленных деталей ( )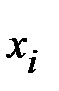

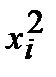
Тогда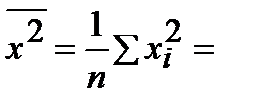

и дисперсия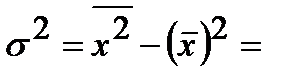

4) Коэффициент вариации вычисляется, как отношение среднего квадратического отклонения к среднему ожидаемому значению и показывает степень отклонения получаемых результатов: .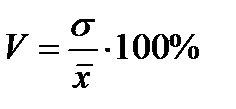

Среднее квадратическое отклонение находим, как корень квадратный из дисперсии, и искомый коэффициент вариации: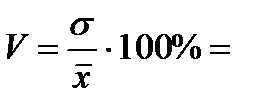

5) Коэффициент осциляции вычисляется, как отношение размаха вариации к среднему ожидаемому значению и показывает отклонение размаха вариации от среднего значения признака: .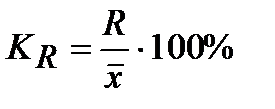

Размах вариации находим, как разность между максимальным и минимальным значениям признака: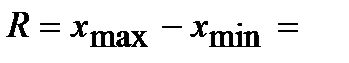

И искомый коэффициент осциляции: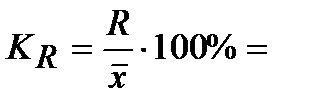

Относительное линейное отклонение (или линейный коэффициент вариации) вычисляем, как отношение среднего линейного отклонения к средней арифметической:

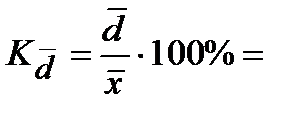
Задача 2 . Имеются данные об урожайности пшеницы в центнерах с 1 га:

Урожайность (цент. с 1 га)	Посевная площадь (га)

Определить среднее линейное отклонение.

12 Следующая ⇒