
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Обратные функции. Область определения и область значений обратной функции. График обратной функции.
Тема: Обратные функции. Область определения и область значений обратной функции. График обратной функции.
Цели:
- дать понятие обратной функции, область определения и область значения обратной функции, учить находить обратную функцию.
Актуализация знаний.
Теоретический материал
1. 1. Рассмотри квадратичную функцию, например у=х2. (x> =0)
Заполните таблицу и постройте ее график:
| x | |||||
| у=х2 |
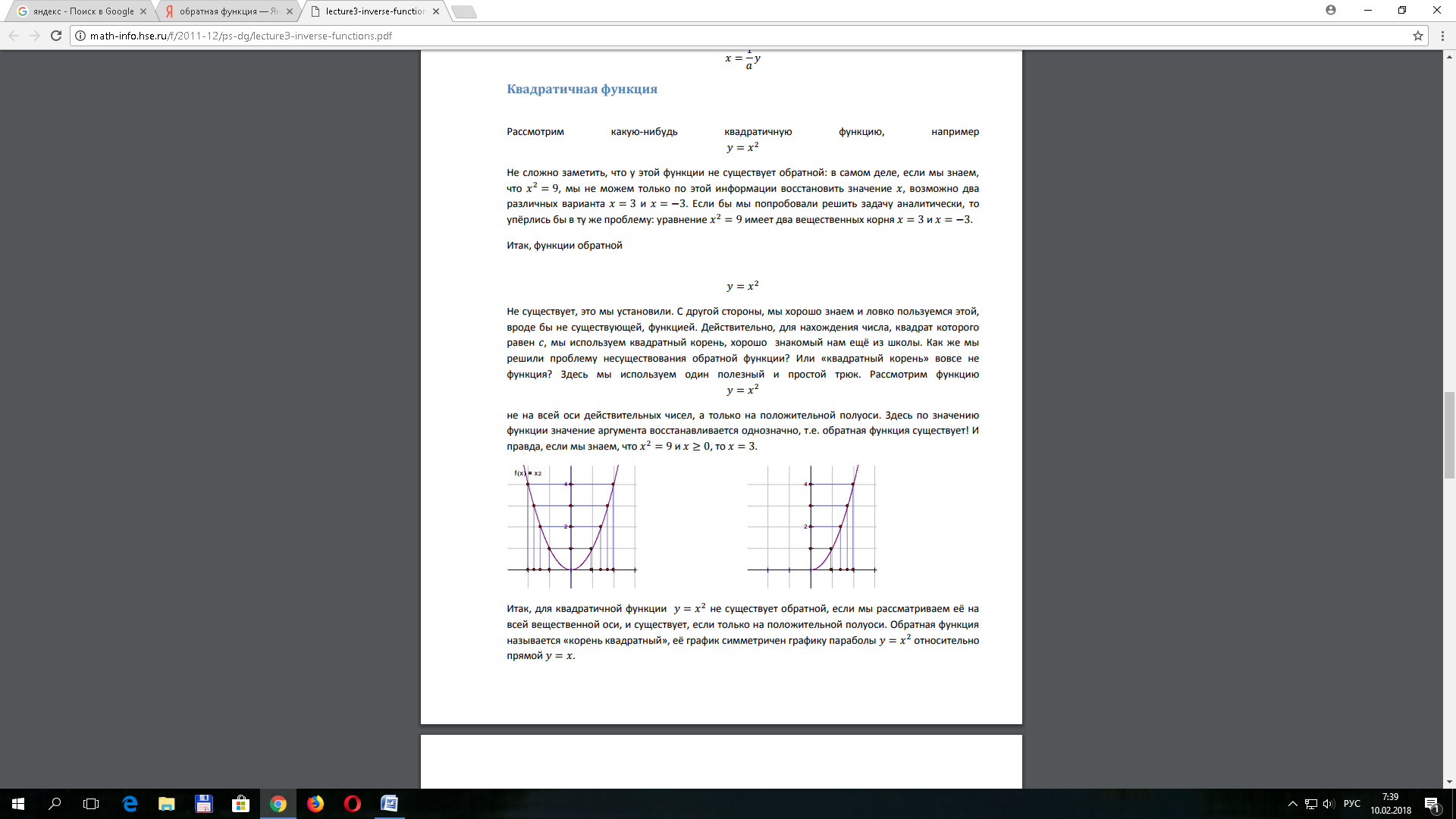
Укажите область определения D(f)-? Укажите область значения E(f)-?
2. Рассмотри квадратичную функцию у= 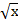
Заполните таблицу и постройте ее график в той же системе координат:
| x | |||||
у= 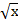
|
Укажите область определения D(f -1) -? Укажите область значения E(f -1) -?
 Таким образом функции у=х2 и у=
Таким образом функции у=х2 и у= 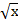 - обратные функции.
- обратные функции.
Свойства обратных функций:
10 Область определения обратной функции f-1 совпадает с множеством значений исходной f, а множество значений обратной функции f-1 совпадает с областью определения исходной функции f: D(f -1) = E(f), E(f -1) = D(f).
20 Если функция имеет обратную, то график обратной функции симметричен графику данной функции относительно прямой у = х
30 Монотонная функция является обратимой: если функция f возрастает, то обратная к ней функция f-1 также возрастает; если функция f убывает, то обратная к ней функция f-1 также убывает.
Сделаем вывод. Если обратимая функция 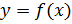 задана формулой, то для нахождения обратной функции нужно решить уравнение
задана формулой, то для нахождения обратной функции нужно решить уравнение 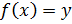 относительно
относительно 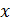 , а затем поменять местами
, а затем поменять местами 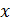 и
и 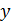 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|