
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
1.Производная показательной функции.
Специальность: 34. 02. 01 Сестринское дело
Дисциплина: ОУД. 05 «Математика»
15. 02, 191
Занятие 66
Тема: Производные некоторых элементарных функций.
План
1. Производная показательной функции;
2. Производная логарифмической функции;
3. Производные тригонометрических функций.
4. Применение правил дифференцирования и формул производных к решению задач.
Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрические функции, а также их различные комбинации.
1. (ex) ' = ex
2. (ekx+b) ' =kekx+b
3. (ax) ' =axlna
4. 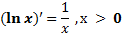
5. 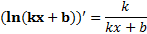
6. 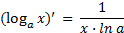
7. (sin x) ' =cosx
8. (cos x) ' = -sinx
Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрические функции, а также их различные комбинации. При решении многих практических задач часто приходится находить производные таких функций.
1. Производная показательной функции.
Показательная функция f(x)=ax, где а> 0, a ≠ 1, определена на всей числовой прямой и имеет производную в каждой ее точке. Любую показательную функцию можно выразить через показательную функцию с основанием у по формуле:
ax=exln a (1)
так как exln a= (eln a)х= ах.
Стоит отметить свойств о функции ех: производная данной функции равна ей самой
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|