
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определение.. Определение.
Определение.
Высота усеченной пирамиды – это перпендикуляр, проведенный из любой точки одного основания к плоскости второго основания.
Апофема исходной пирамиды – РМ (М – середина АВ), апофема усеченной пирамиды – 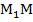 (рис. 4).
(рис. 4).
Определение.
Апофема усеченной пирамиды – высота любой боковой грани.
Ясно, что все боковые ребра усеченной пирамиды равны между собой, то есть боковые грани – равные равнобедренные трапеции.
Теорема о площади боковой поверхности правильной усеченной пирамиды
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
Доказательство (для правильной четырехугольной усеченной пирамиды – рис. 4):
Итак, необходимо доказать:
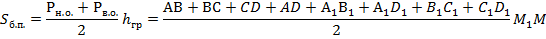
Площадь боковой поверхности здесь будет состоять из суммы площадей боковых граней – трапеций. Поскольку трапеции одинаковы, имеем:
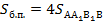
Площадь равнобедренной трапеции – это произведение полусуммы оснований и высоты, апофема является высотой трапеции. Имеем:
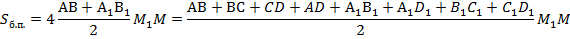
Что и требовалось доказать.
Для n-угольной пирамиды:
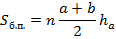
Где n – количество боковых граней пирамиды, a и b – основания трапеции, 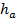 – апофема.
– апофема.
Решение задачи 1
Стороны основания правильной усеченной четырехугольной пирамиды 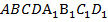 равны 3 см и 9 см, высота – 4 см. Найти площадь боковой поверхности.
равны 3 см и 9 см, высота – 4 см. Найти площадь боковой поверхности.
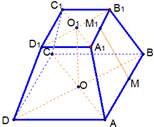
Рис. 5. Иллюстрация к задаче 1
Решение. Проиллюстрируем условие:
Задано: 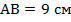 ,
, 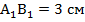 ,
, 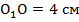
Через точку О проведем прямую MN параллельно двум сторонам нижнего основания, аналогично через точку 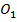 проведем прямую
проведем прямую 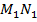 (рис. 6). Поскольку в основаниях усеченной пирамиды квадраты и построения параллельны, получим трапецию, равную боковым граням. Причем ее боковая сторона будет проходить через середины верхнего и нижнего ребра боковых граней и являться апофемой усеченной пирамиды.
(рис. 6). Поскольку в основаниях усеченной пирамиды квадраты и построения параллельны, получим трапецию, равную боковым граням. Причем ее боковая сторона будет проходить через середины верхнего и нижнего ребра боковых граней и являться апофемой усеченной пирамиды.
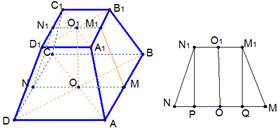
Рис. 6. Дополнительные построения
Рассмотрим полученную трапецию 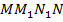 (рис. 6). В этой трапеции известно верхнее основание, нижнее основание и высота. Требуется найти боковую сторону, которая является апофемой заданной усеченной пирамиды. Проведем
(рис. 6). В этой трапеции известно верхнее основание, нижнее основание и высота. Требуется найти боковую сторону, которая является апофемой заданной усеченной пирамиды. Проведем 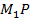 перпендикулярно MN. Из точки
перпендикулярно MN. Из точки 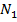 опустим перпендикуляр NQ. Получим, что большее основание разбивается на отрезки по три сантиметра (
опустим перпендикуляр NQ. Получим, что большее основание разбивается на отрезки по три сантиметра ( 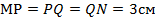 ). Рассмотрим прямоугольный треугольник
). Рассмотрим прямоугольный треугольник 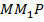 , катеты в нем известны, это египетский треугольник, по теореме Пифагора определяем длину гипотенузы: 5 см.
, катеты в нем известны, это египетский треугольник, по теореме Пифагора определяем длину гипотенузы: 5 см.
Теперь есть все элементы для определения площади боковой поверхности пирамиды:
Вв 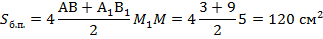
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|