Определение.

10 класс. Геометрия 31. 03. 22 г.

Тема урока: «Усеченная пирамида».

Ребята, внимательно изучите предложенный материал, разберите предложенную решенную задачу.

Выполните рисунок усеченной пирамиды, запишите в тетрадь решение задачи.

Вспомним понятие n-угольной пирамиды на примере треугольной пирамиды. Задан треугольник АВС. Вне плоскости треугольника взята точка Р, соединенная с вершинами треугольника. Полученная многогранная поверхность и называется пирамидой (рис. 1).

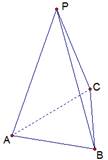
Рис. 1. Треугольная пирамида

Рассечем пирамиду плоскостью 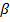, параллельной плоскости основания пирамиды 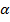. Полученная между этими плоскостями фигура 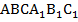и называется усеченной пирамидой (рис. 2).

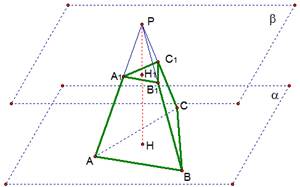
Рис. 2. Усеченная пирамида

Основные элементы:

-верхнее основание ;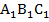

-нижнее основание АВС;

-боковая грань ;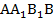

-если РН – высота исходной пирамиды, то 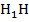– высота усеченной пирамиды.

Свойства усеченной пирамиды вытекают из способа ее построения, а именно из параллельности плоскостей оснований:

-все боковые грани усеченной пирамиды являются трапециями. Рассмотрим, например, грань 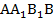. У нее 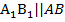по свойству параллельных плоскостей (поскольку плоскости параллельны, то боковую грань исходной пирамиды АВР они рассекают по параллельным прямым), в то же время 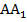и 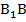не параллельны. Очевидно, что четырехугольник 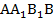является трапецией, как и все боковые грани усеченной пирамиды.

-отношение оснований одинаково для всех трапеций:

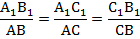
Имеем несколько пар подобных треугольников с одинаковым коэффициентом подобия. Например, треугольники 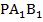и РАВ подобны в силу параллельности плоскосте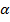й и 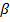, коэффициент подобия:

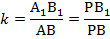
В то же время подобны треугольники 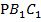и РВС с коэффициентом подобия:

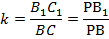
Очевидно, что коэффициенты подобия для всех трех пар подобных треугольников равны, поэтому отношение оснований одинаково для всех трапеций.

Правильная усеченная пирамида, понятие, основные определения

Правильной усеченной пирамидой называется усеченная пирамида, полученная сечением правильной пирамиды плоскостью, параллельной основанию (рис. 3).

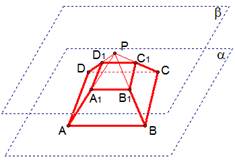
Рис. 3. Правильная усеченная пирамида

Определение.

Правильной называется пирамида, в основании которой лежит правильный n-угольник, а вершина проектируется в центр этого n-угольника (центр вписанной и описанной окружности).

В данном случае в основании пирамиды лежит квадрат, и вершина проектируется в точку пересечения его диагоналей. У полученной правильной четырехугольной усеченной пирамиды ABCD – нижнее основание, 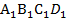– верхнее основание. Высота исходной пирамиды – РО, усеченной пирамиды – 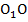(рис. 4).

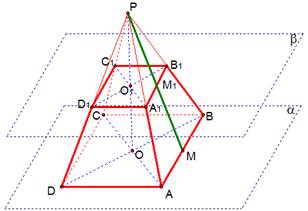
Рис. 4. Правильная четырехугольная усеченная пирамида

12 Следующая ⇒