Конспект объясняющего модуля. Решение практических задач с использованием формулы длины окружности, площади круга и кругового сектора. 01.02.22 Урок геометрии. Задача №1.. Задача №2.

Конспект объясняющего модуля

Решение практических задач с использованием формулы длины окружности, площади круга и кругового сектора

01. 02. 22 Урок геометрии

9 класс

Тема урока Площадь круга и его частей

Площадь всего круга: .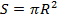

Площадь кругового сектора, ограниченного дугой в 1° равна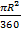

Площадь S кругового сектора с произвольным углом α будет равна: .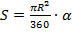

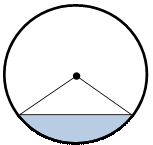Круговым сегментом или просто сегментом называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы этой дуги

Задача №1.

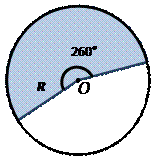Площадь не закрашенного сектора круга равна 10π. Вычислите радиус R.

Воспользуемся формулой вычисления площади сектора круга: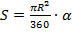

Отсюда выразим значение R: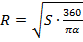

Обратим внимание, что в условии речь идет о площади не закрашенной части круга, а на рисунке дан угол закрашенной части круга.

Так как полный круг содержит 360°, вычтем известное нам значение угла закрашенной части сектора: α = 360° – 260° = 100°

Подставим значения в формулу и после преобразований получим искомое значение радиуса сектора круга: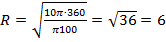

Ответ: 6

Задача №2.

Вычислите хорду окружности MN, если l длина дуги, угол дуги α = 120°.

Для решения задачи нужно вычислить значение радиуса окружности и затем по правилу прямоугольного треугольника рассчитать длину хорды.

Вычислим радиус окружности.

Длины дуги окружности с углом альфа: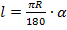

Выразим отсюда значение радиуса и подставим в формулу значение угла α , после преобразований получим: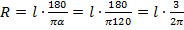

Обратим внимание на рисунок.

Два радиуса и хорда образуют равнобедренный треугольник.

Радиусы, то есть стороны треугольника вычислены. Можно приступать к расчету длины хорды окружности, являющейся основанием треугольника.

Проведем высоту треугольника из его вершины к основанию.

Она является биссектрисой угла, перпендикуляром к основанию треугольника и делит основание пополам.

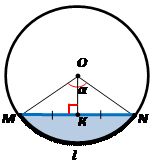
Получен прямоугольный треугольник с двумя известными углами ∠ OKM = 90°, ∠ MOK = 60°.

Применяя правила соотношения сторон и углов в прямоугольном треугольнике рассчитаем половину длины хорды: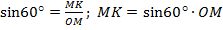

Подставим значения: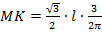

После преобразований получим длину половину хорды: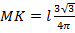

Для получения полной длины хорды умножим полученное значение на два и после преобразований получим: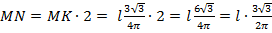

Задача решена.