10 класс. Алгебра. Тема: Логарифмические уравнения и неравенства.. Повторить §19-20.. 2. Метод потенцирования.. 3. Уравнения, решаемые с помощью применения основного логарифмического тождества.

Стр 1 из 2Следующая ⇒

25. 03. 2022

10 класс. Алгебра

Тема: Логарифмические уравнения и неравенства.

Повторить §19-20.

1) Рассмотреть ОСНОВНЫЕ СПОСОБЫ РЕШЕНИЯ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ:

1. Решение уравнений на основании определения логарифма.

log_a х = с (а > 0, а≠ 1) имеет решение х = а^с.

На основе определения логарифма решаются уравнения, в которых:

· по данным основаниям и числу определяется логарифм,

· по данному логарифму и основанию определяется число,

· по данному числу и логарифму определяется основание.

Примеры:

log₂ 128= х, log₁₆х = , log_х 27= 3,

2^х= 128, х = 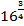, х³ =27,

2^х = 2⁷, х =2³, х³ = 3³ ,

х =7. х = 8. х =3.

2. Метод потенцирования.

Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их т. е.

log_a f(х) = log_a g(х), то f(х) = g(х), при условии, что f(х)> 0, g(х)> 0, а > 0, а≠ 1.

Пример:

Решите уравнение =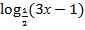

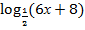
ОДЗ:

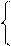3х-1> 0; х>

6х+8> 0.

3х-1=6х+8

-3х=9

х=-3

-3 > - неверно

Ответ: решений нет.

3. Уравнения, решаемые с помощью применения основного логарифмического тождества.

Пример:

Решите уравнение 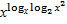=log₂(6-х)

ОДЗ:

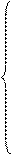6-х> 0;

х> 0;

х≠ 1;

log₂х²> 0;

х²> 0.

Решение системы: (0; 1)Ụ (1; 6).

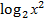= log₂(6-х)

х² = 6-х

х²+х-6=0

х=-3 не принадлежит ОДЗ.

х=2 принадлежит ОДЗ.

Ответ: х=2

4. Метод приведения логарифмов к одному и тому же основанию.

Пример:

Решите уравнение log₁₆х+ log₄х+ log₂х=7

ОДЗ: х> 0

log₂х+ log₂х+ log₂х=7

log₂х=7

log₂х=4

х=16 – принадлежит ОДЗ.

Ответ: х=16.

5. Уравнения, решаемые с помощью применения свойств логарифма.

Пример:

Решите уравнение log₂ (х +1) - log₂ (х -2 ) = 2.

ОДЗ:

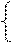х+1> 0;

х-2> 0. х> 1.

Воспользуемся формулой преобразования разности логарифмов логарифм частного, получаем

log₂ 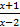= 2, откуда следует 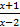= 4.

Решив последнее уравнение, находим х = 3, 3> 1 - верно

Ответ: х = 3.

6. Уравнения, решаемые введением новой переменной.

Пример:

Решите уравнение lg²х - 6lgх+5 = 0.

ОДЗ: х> 0.

Пусть lgх = р, тогда р²-6р+5=0.

р₁=1, р₂=5.

Возвращаемся к замене:

lgх = 1, lgх =5

х=10, 10> 0 – верно х=100000, 100000> 0 – верно

Ответ: 10, 100000

7. Уравнения, решаемые с помощью разложения на множители.

Пример:

Решите уравнение log₄(2х-1)∙ log₄х=2 log₄(2х-1)

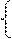ОДЗ:

2х-1> 0;

х > 0. х> .

log₄(2х-1)∙ log₄х - 2 log₄(2х-1)=0

log₄(2х-1)∙ (log₄х - 2)=0

log₄(2х-1)=0 или log₄х-2=0

2х-1=1 log₄х = 2

х=1 х=16

1; 16 – принадлежат ОДЗ

Ответ: 1; 16

12 Следующая ⇒