Исполнитель Автомат

⇐ ПредыдущаяСтр 5 из 7Следующая ⇒

Исполнитель Автомат работает с числами от 0 до 9999. Его задача: получить заданное число.

Команды исполнителя Автомата

ПРИБАВИТЬ - к числу прибавляется 1 (П).

УМНОЖИТЬ - число умножается на 2 (У).

Алгоритмы решения оформляются в виде таблицы, в которых используются следующие обозначения:

К – команда; Р – результат выполнения команды исполнителя.

Пример 1. Получить число 4.

№
К	П	П	П	П
Р

Запись арифметического выражения:

0 + 1 + 1 + 1 + 1 = 4

Пример 2. Получить число 4 другим способом.

№
К	П	П	У
Р

Запись арифметического выражения:

(0 + 1 + 1) × 2 = 4

Пример 3. Получить число 6.

№
К	П	У	П	У
Р

Запись арифметического выражения:

((0 + 1) × 2 + 1) × 2 = 6

Обратные задачи

Обратная задача необходима для того, чтобы определить минимальное количество команд в получении заданного числа.

Для записи алгоритма обратной задачи используют операции, обратные операциям исполнителя Автомата:

ДЕЛИТЬ- число делится на 2 (Д);

ВЫЧЕСТЬ- из числа вычитается 1 (В).

Если число четное - то в обратной задаче надо число разделить на 2, т. е. использовать команду ДЕЛИТЬ, если число нечетное - то из числа вычитается 1, т. е. используется команда ВЫЧЕСТЬ. После решения обратной задачи записывается прямая задача и арифметическое выражение.

Примеры алгоритмов:

Пример 1. За наименьшее число команд получить число 29.

Алгоритм обратной задачи

№
К	В	Д	Д	В	Д	В	Д	В
Р

Алгоритм прямой задачи:

№
К	П	У	П	У	П	У	У	П
Р

Арифметическое выражение: (((0 + 1) × 2 + 1 ) × 2 + 1 ) × 2 × 2 + 1 = 29

Задачи

Задача 1. Каково предназначение исполнителя Автомата?

Задача 2. Назвать СКИ исполнителя Автомата. Как выполняются команды?

Задача 3. Для чего и как составляют обратную задачу?

Задача 4. Какая ошибка допущена на рисунке?

Задача 5. Приведите примеры команд, когда исполнитель Автомат может ответить “НЕ ПОНИМАЮ”?

Задача 6. С помощью исполнителя Автомата получить число 9 за 5 команд.

Задача 7. С помощью исполнителя Автомата получить числа: 11, 17 и 24 за 6 команд, 15, 19 и 33 за 7 команд, 35 за 8 команд.

Задача 8. За наименьшее количество команд получить число: 27, 28, 34, 43, 55, 57, 60, 127 и 325.

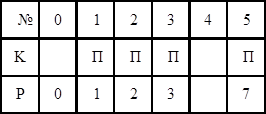Задача 9. Восстанови алгоритмы:

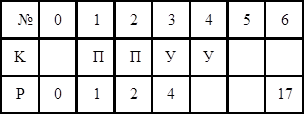
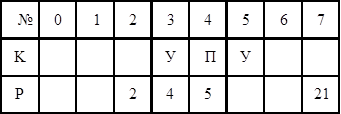
Задача 10. На очередной команде исполнитель Автомат ответил “НЕ МОГУ”. Что произошло?

Задача 11. Определить, какое минимальное количество команд потребуется подать исполнителю Автомату для получения чисел 31 и 133. Записать алгоритмы прямых задач и арифметические выражения.

Задача 12. Восстановить алгоритмы:

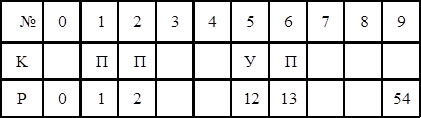
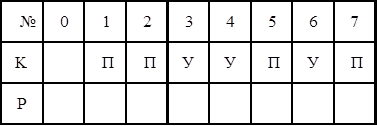
Записать арифметические выражения, соответствующие восстановленным алгоритмам. Записать алгоритмы обратных задач.

Задача 13. По арифметическому выражению записать алгоритмы:

a) ((1 × 2 × 2 + 1) × 2 + 1) × 2

b) ((1 × 2 + 1) × 2 × 2 × 2 + 1 + 1) × 2

c) ((1 × 2 + 1) × 2 × 2 + 1) × 2 + 1

d) (((1 + 1 + 1) × 2 + 1) × 2 × 2 + 1) × 2 + 1

e) (((1 × 2 + 1) × 2 + 1 + 1) × 2 × 2 + 1) × 2

Задача 14. Составьте прямую задачу по арифметическому выражению:

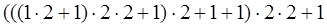
Можно ли получить это число проще?

Задача 15. Известно, что после очередной команды получено число 95. Какая команда была отдана последней? Ответ объяснить.

Задача 16. Сможет ли Автомат выполнить задачу? Ответ пояснить.

((1 × 2 × 2 + 1) × 2 × 2 + 1) × 3 + 1

Задача 17. Переписать арифметическое выражение так, чтобы его мог выполнить исполнитель Автомат: ((1 + 2) × 2 + 1) × 2.

Задача 18. В результате очередной команды получено число 5000. Какая команда может быть следующей? Ответ пояснить.

Задача 19. Какое минимальное количество команд потребуется исполнителю Автомату для получения максимально допустимого числа?

⇐ Предыдущая 1 2 3 456 7 Следующая ⇒