2. Пределы функций

Предел функции. Некоторые замечательные пределы.

Бесконечно малая и бесконечно большая величины.

Конечный предел. Бесконечный предел.

Понятие бесконечности.

Предел функции. ЧислоL называется пределом функции y = f ( x ) при x, стремящемся к a:

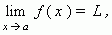
если для любого 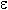> 0 найдётся такое положительное число 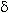= 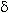( 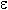), зависящее от 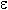, что из условия | x - a | < 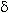следует | f ( x ) – L | < .

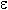Это определение означает, что L есть предел функции y = f ( x ), если значение функции неограниченно приближается к L, когда значение аргумента x приближается к a. Геометрически это значит, что для любого 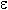> 0 можно найти такое число 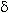, что если x находится в интервале 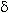( a - , a + 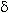), то значение функции лежит в интервале 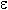( L - , L + 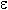). Отметим, что в соответствии с этим определением аргумент функции лишь приближается к a , не принимая этого значения! Это следует учитывать при вычислении предела любой функции в точке её разрыва, где функция не существует.

П р и м е р. Найти

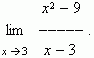
Р е ш е н и е. Подставляя x = 3 в выражение 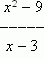получим не имеющее смысла выражение 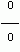. Поэтому решим по-другому:

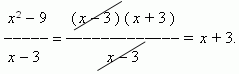
Сокращение дроби в данном случае корректно, так как x 3, он лишь приближается к 3. Теперь мы имеем:

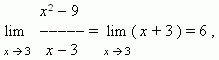
поскольку, если x стремится к 3, то x + 3 стремится к 6.

⇐ Предыдущая 123 Следующая ⇒