Задача №1

Тонкая линза. Задачи. Часть 3

Задача №1

Условие:

“На оси x в точке 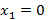находится оптический центр тонкой рассеивающей линзы с 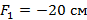, а в точке 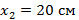центр тонкой собирающей линзы с 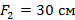. Главные оптические оси линз лежат на оси x . Свет от точечного источника, расположенного в точке x < 0, пройдя данную оптическую систему, распространяется параллельным пучком. Найти координату точечного источника. ”

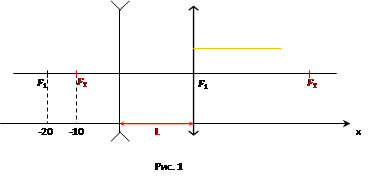После прохождения оптической системы луч выходит параллельно главной оптической оси. (рис. 1)

Правило гласит, что если луч параллелен оптической оси, то он обязательно пройдёт через её фокус. Получается, что в точке 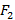с координатой -10 будет источник света для собирающей линзы. В то же время источник свет 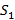является изображением для второй линзы. (рис 2)

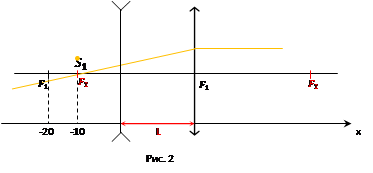
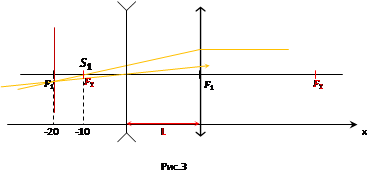
Получается задачу мы чертим с конца, и теперь надо узнать, где находится источник света для рассеивающей линзы. Для этого начертим фокальную плоскость в точке 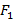и вспомогательный луч, параллельный исходному. Исходный луч мы нарисовать не можем, а вот вспомогательный вполне. (рис 3)

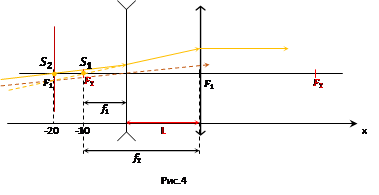
После этого проведём исходный луч как показано на рисунке 4

Тогда формула тонкой линзы будет выглядеть так:

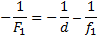
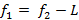
Подставим значения и вычислим d: d = 20. Однако в задаче просят найти координату, а это значит, что x = -20.

Ответ: x = -20.

12 3 Следующая ⇒