Пример построения гистограммы

При обработке валика на токарном станке необходимо выдержать размер Ø 22, 27-0, 44.

Из текущей продукции станка берется выборка из деталей, изготовленных при неизменной настройке, объемом n=90 шт. Результаты измерений занесены в таблицу 1.

Таблица 1 – Результаты измерения диаметра деталей

22, 02	21, 97	22, 03	22, 05	22, 01	22, 04	21, 98	22, 04	21, 99	21, 93	22, 05	21, 98	21, 91
21, 99	22, 05	21, 99	21, 84	21, 81	22, 06	22, 00	22, 04	21, 92	22, 07	21, 92	22, 0	22, 0
21, 98	22, 06	22, 03	22, 05	21, 98	22, 06	22, 04	21, 88	22, 08	21, 98	22, 04	22, 0	22, 01
21, 92	21, 96	21, 99	21, 99	21, 94	21, 90	21, 93	21, 94	22, 07	22, 09	21, 82	21, 92	21, 99
21, 94	22, 06	22, 02	21, 99	22, 15	22, 00	21, 88	21, 97	21, 99	22, 13	21, 88	22, 03	21, 96
21, 89	21, 97	21, 93	21, 95	21, 98	22, 01	22, 05	22, 04	22, 09	21, 87	22, 09	22, 01	22, 07
21, 89	22, 0	21, 96	22, 06	21, 93	22, 02	21, 95	22, 06	22, 03	22, 05	22, 03	21, 89

Находим наибольшее и наименьшее значения:

Размах равен

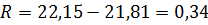
Принимаем количество интервалов равное 9 (k=9). Определяем ширину интервала

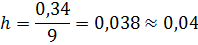
Границы интервалов устанавливаем следующими: левая граница первого интервала принимается 21, 80 (меньше X_min), правая отстоит на ширину интервала и составляет 21, 84

Последующие границы 21, 88; 21, 92; 21, 96 и т. д. Правая граница последнего интервала 22, 16, что больше наибольшего из имеющихся значений. Определяем частоту попадания размеров в установленные интервалы (m_i). Результаты подсчетов сводим в таблицу 2. Накопленная частота определяется путем прибавления каждого последующего значения частоты к сумме предыдущих значений

Таблица 2 – Бланк для подсчета частоты

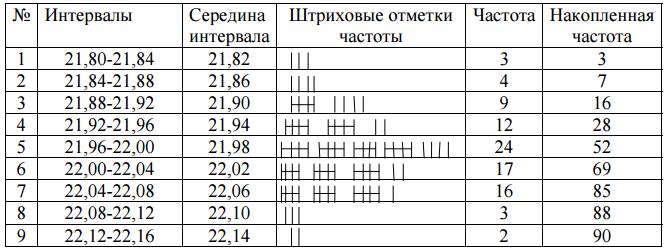
Строим гистограмму распределения (рисунок 1).

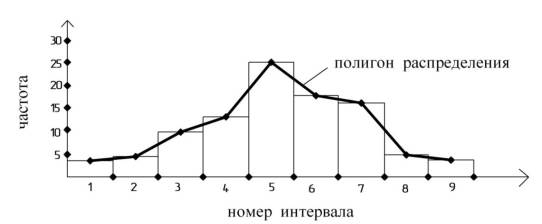
Рисунок 1 – Гистограмма распределения значений показателя качества

Ломаная кривая называется полигоном распределения или эмпирической кривой распределения случайной величины. Полигон используют для удобства анализа технологического процесса.

⇐ Предыдущая 12