
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание 5. Задание 6. Ответ: Это окружность.. Задание 7
Задание 5
Доказать неравенство
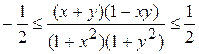 .
.
Решение. Рассмотрим три вектора 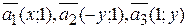 . Пусть угол между векторами
. Пусть угол между векторами 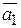 и
и 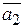 равен
равен 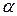 , а между векторами
, а между векторами 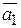 и
и 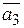 равен
равен 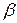 . Тогда
. Тогда 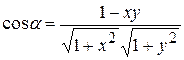 ,
, 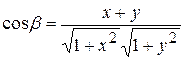 ,
, 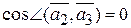 . Следовательно,
. Следовательно,  и
и 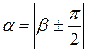 . Поэтому
. Поэтому 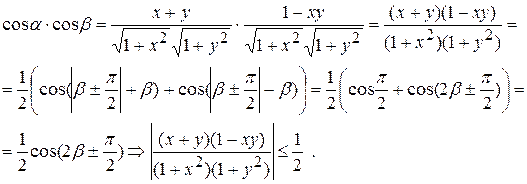
Задание 6
 Дан треугольник. Найти геометрическое место центров правильных треугольников, описанных около него (см. рисунок).
Дан треугольник. Найти геометрическое место центров правильных треугольников, описанных около него (см. рисунок).
Ответ: Это окружность.
Решение. Пусть дан треугольник 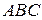 . Рассмотрим три правильных треугольника
. Рассмотрим три правильных треугольника 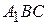 ,
, 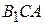 и
и 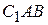 , построенных на сторонах
, построенных на сторонах 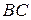 ,
, 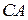 и
и 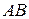 во внешнюю сторону, и их описанные окружности
во внешнюю сторону, и их описанные окружности 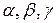 (см. рисунок). Вершины любого правильного треугольника
(см. рисунок). Вершины любого правильного треугольника 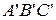 , описанного около треугольника
, описанного около треугольника 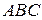 , лежат на окружностях
, лежат на окружностях 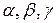 . Центр Z треугольника
. Центр Z треугольника 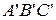 – точка пересечения двух биссектрис его углов
– точка пересечения двух биссектрис его углов 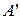 и
и 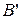 . Эти биссектрисы пересекаются под углом 120 градусов и проходят через две фиксированные точки X и Y – середины дуг
. Эти биссектрисы пересекаются под углом 120 градусов и проходят через две фиксированные точки X и Y – середины дуг 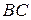 и
и 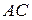 окружностей
окружностей 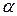 и
и 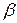 , не содержащих точек
, не содержащих точек 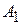 и
и 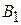 . Т. е. искомое г. м. т. – окружность. Она проходит через точку Торричелли и середины дуг
. Т. е. искомое г. м. т. – окружность. Она проходит через точку Торричелли и середины дуг 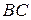 ,
, 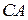 и
и 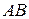 окружностей
окружностей 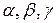 .
.
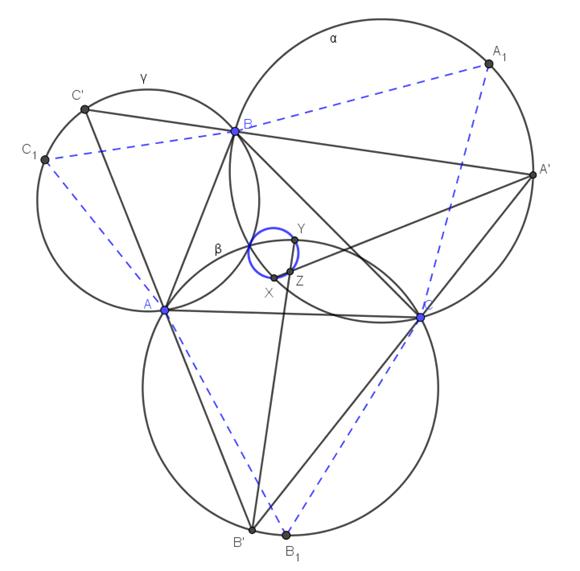
Задание 7
a) Доказать, что наименьшее общее кратное чисел 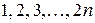 равно наименьшему общему кратному чисел
равно наименьшему общему кратному чисел 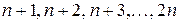 .
.
Решение. Пусть 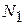 есть НОК
есть НОК 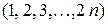 , а
, а 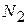 – НОК
– НОК 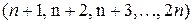 .
.
Покажем, что произвольное число d из множества чисел 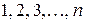 делит
делит 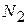 . В самом деле, последовательно удваивая d, на некотором этапе мы попадем на отрезок
. В самом деле, последовательно удваивая d, на некотором этапе мы попадем на отрезок 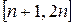 . Получившееся число d’, кратное d и делит
. Получившееся число d’, кратное d и делит 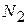 .
.
Поэтому 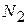 является наименьшим общим кратным и для чисел
является наименьшим общим кратным и для чисел 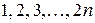 .
.
Задание 8
Пусть квадратная матрица A размером 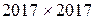 такая, что для некоторого натурального
такая, что для некоторого натурального 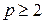 выполняется равенство
выполняется равенство 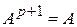 .
.
Найти значение суммы  , если
, если 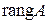 – ранг матрицы A, E –единичная матрица размером
– ранг матрицы A, E –единичная матрица размером 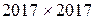 .
.
Ответ: 2017.
Решение. Заметим, что 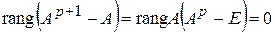 . Так как
. Так как 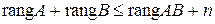 (неравенство Сильвестра), то
(неравенство Сильвестра), то 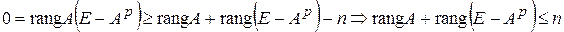 . С другой стороны,
. С другой стороны, 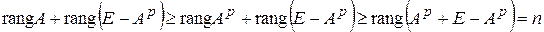 . Следовательно,
. Следовательно, 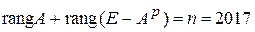 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|