
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание 1. Задание 2. Ответ: Да.. Задание 3. Задание 4
Задание 1
Функция 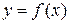 при любом значении x удовлетворяет соотношению
при любом значении x удовлетворяет соотношению
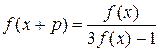 , где
, где 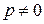 – некоторое число. Докажите, что функция
– некоторое число. Докажите, что функция 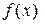 периодична.
периодична.
Решение. Покажем, что 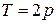 – период функции
– период функции 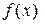 . Находим,
. Находим,
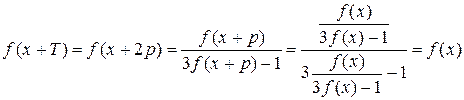 .
.
Функция
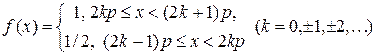
удовлетворяет условию задачи.
Задание 2
Найдется ли простое число 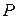 , большее
, большее 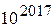 , такое, что число
, такое, что число 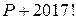 составное?
составное?
Ответ: Да.
Решение. Пусть 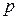 простое число, большее
простое число, большее 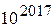 . Прибавим
. Прибавим 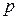 раз к нему число
раз к нему число  . Получим составное число
. Получим составное число 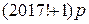 . Ясно, что на одном из шагов прибавления
. Ясно, что на одном из шагов прибавления  из некоторого простого числа
из некоторого простого числа 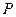 получилось составное.
получилось составное.
Задание 3
Докажите, что 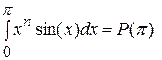 для некоторого многочлена
для некоторого многочлена 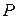 степени n с целыми коэффициентами.
степени n с целыми коэффициентами.
Решение. Будем действовать по индукции, одновременно доказывая, что 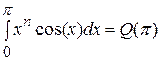 для некоторого многочлена
для некоторого многочлена 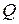 степени n с целыми коэффициентами.
степени n с целыми коэффициентами.
Интегрируя по частям (при 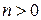 ) имеем индукционный переход:
) имеем индукционный переход:
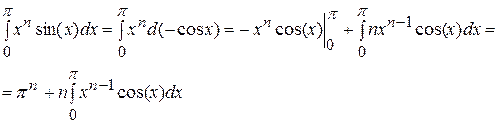
и
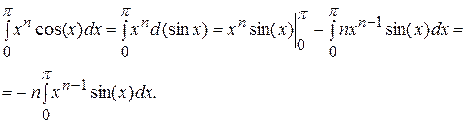
При 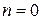 имеем
имеем 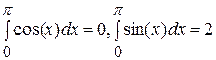 .
.
Задание 4
В 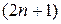 -угольнике проведены все диагонали. Можно ли на сторонах и диагоналях поставить стрелки так, чтобы сумма получившихся векторов равнялась нулю?
-угольнике проведены все диагонали. Можно ли на сторонах и диагоналях поставить стрелки так, чтобы сумма получившихся векторов равнялась нулю?
Ответ: Всегда можно.
Решение. Все эти линии разбиваются на замкнутые ломаные: стороны многоугольника, если соединять через одну, если соединять через 2 (может образоваться одна или три замкнутые ломаные) и т. д. (При четном числе вершин возникают пары диаметрально противоположных точек, но у нас число вершин нечетное. )
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|